山东省东营市广饶县乐安街道乐安中学2023-2024学年九年级上学期开学数学试题(pdf版 无答案)
文档属性
| 名称 | 山东省东营市广饶县乐安街道乐安中学2023-2024学年九年级上学期开学数学试题(pdf版 无答案) |  | |
| 格式 | |||
| 文件大小 | 511.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 18:19:18 | ||
图片预览


文档简介
2023-2024 学年第一学期教学质量反馈
九年级数学试题
(总分 120 分,考试时间 120 分钟)
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分,第一卷为选择题,30分;第二卷为非选择题,90分;本试题共 6页。
2.数学试题答题卡共 4页,答题前,考生务必将自己的姓名、班级、学校、准考证号等填写在试题和答题
卡上。
3. 第Ⅰ卷每题选出答案后,都必须用 2B 铅笔把答题卡上对应题目的答案标号【ABCD】涂黑。如需改动,
先用橡皮擦干净,再涂改其它答案。第二卷按要求用 0.5mm碳素笔答在答题卡的相应位置上。
第Ⅰ卷(选择题 共 30分)
一、选择题(本题共 10个小题,每小题 3分,共 30分)
1.化学实验室中竖直放置的玻璃漏斗,其主视图是( )
A. B. C. D.
2.二次函数 y x2 2x 2的图象的对称轴是( )
A. x= 1 B. x 2 C. x 1 D. x 2
3.一个正多边形的中心角为30 ,这个正多边形的边数是( )
A.8 B.12 C.3 D.6
4.如图,在△ABC中, C 90 , B 42 , BC 8,若用科学计算器求 AC的长,则下列按键顺序正
确的是( )
A. 8 sin 4 2 B. 8 cos 4 2 C. 8 tan 4 2 D. 8 tan 4 2
(第 4 题图) (第 5 题图)
5.如图,AB为 O的直径,C,D为⊙O上的两点,若 ABD=54 ,则 C的度数为( )
A.34 B.36 C. 46 D.54
6.从下面四个图形中任意选取一个图形,所选图形既是中心对称图形,又是轴对称图形的概率是( )
A. 1 B. 1 C. 3 D.1
4 2 4
九年级数学试题 第 1 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
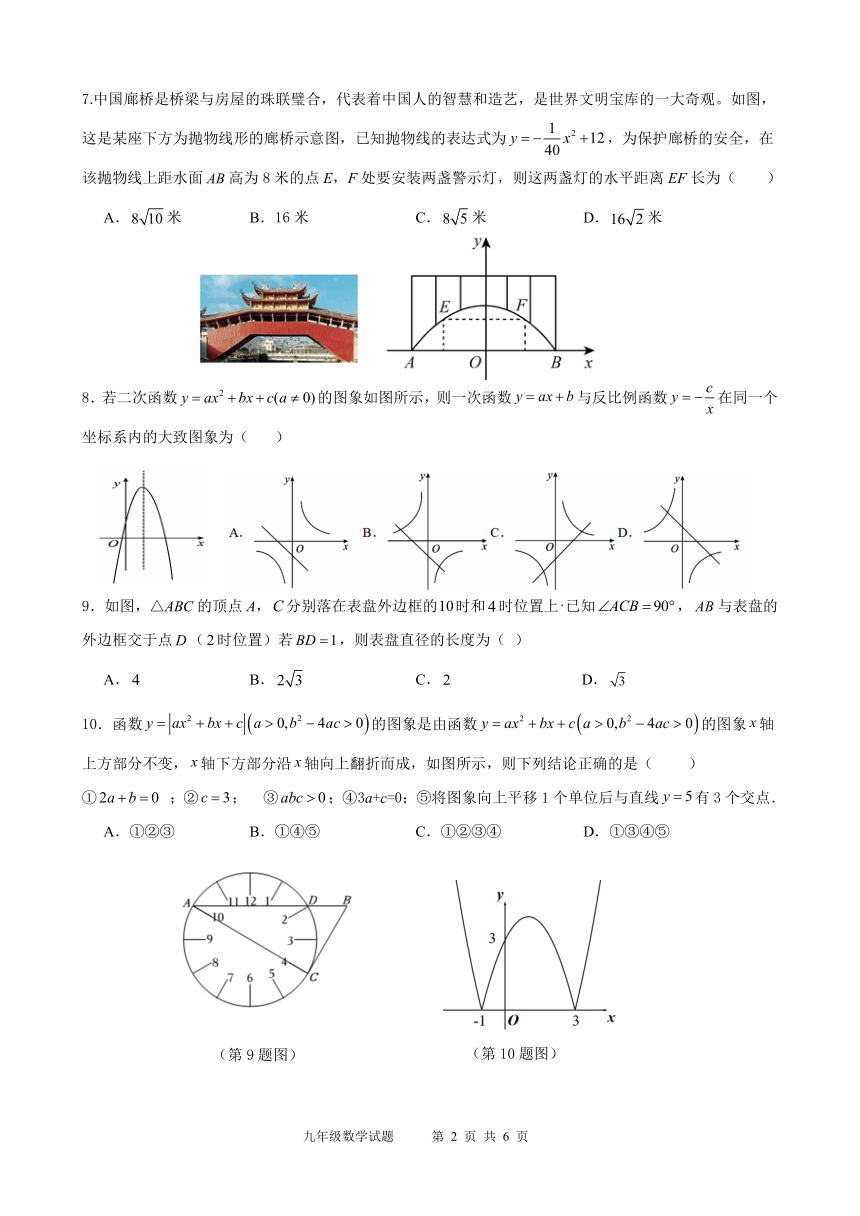
7.中国廊桥是桥梁与房屋的珠联璧合,代表着中国人的智慧和造艺,是世界文明宝库的一大奇观。如图,
1 2
这是某座下方为抛物线形的廊桥示意图,已知抛物线的表达式为 y x 12,为保护廊桥的安全,在
40
该抛物线上距水面 AB高为 8 米的点 E,F处要安装两盏警示灯,则这两盏灯的水平距离 EF长为( )
A.8 10米 B.16 米 C.8 5米 D.16 2米
c
8.若二次函数 y ax2 bx c(a 0)的图象如图所示,则一次函数 y ax b与反比例函数 y 在同一个
x
坐标系内的大致图象为( )
9.如图,△ABC的顶点 A,C分别落在表盘外边框的10时和 4时位置上 .已知 ACB 90 , AB与表盘的
外边框交于点D( 2时位置)若 BD 1,则表盘直径的长度为( )
A. 4 B. 2 3 C. 2 D. 3
10.函数 y ax2 bx c a 0,b2 4ac 0 y ax2 2的图象是由函数 bx c a 0,b 4ac 0 的图象 x轴
上方部分不变, x轴下方部分沿 x轴向上翻折而成,如图所示,则下列结论正确的是( )
① 2a b 0 ;② c 3; ③ abc 0;④3a+c=0;⑤将图象向上平移 1 个单位后与直线 y 5有 3 个交点.
A.①②③ B.①④⑤ C.①②③④ D.①③④⑤
(第 9题图) (第 10 题图)
九年级数学试题 第 2 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
第Ⅱ卷(非选择题 共 90 分)
二、填空题(本题共 8 个小题,其中 11-14 题每小题 3 分,15-18 题每小题 4 分,共 28 分,只要求填写
最后结果)
11.抛物线 y 3 x 2 2 4的顶点坐标是 。
2
12. 1 己知△ABC中, A , B都是锐角,且 cos A | tan B 3 | 0,则 C 度。
2
13.如图,圆锥的左视图是边长为 2的等边三角形,则此圆锥的高是________________。
14.如图,一扇形纸扇完全打开后,外侧两竹条 AB和 AC的夹角为 120°,AB长为 30cm,贴纸部分的宽
BD为 20cm,则贴纸部分的面积为________cm2(纸扇有两面,结果保留π)。
k
15.如图,反比例函数 y 的图象上有一点 P,PA⊥x轴于点 A,点 B在 y轴上,△PAB的面积为 1,则
x
k=_______。
(第 13 题图) (第 14 题图) (第 15 题图)
16.中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”。“方田一段,一
角圆池占之。”意思是说:“一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均
相切)”,如图所示。
问题:若正方形的边长为 10 丈,⊙O的半径为 2 丈,则点 D到⊙O的最短距离为____丈。
17.近年来,随着智能技术的发展,智能机器人已经服务于社会生活的各个方面.图 1所示是一款智能送货
机器人,图 2是其侧面示意图,现测得其矩形底座 ABCD的高 BC为30cm,上部显示屏 EF的长度为30cm,
侧面支架 EC的长度为100cm, ECD 80 , FEC 130 ,则该机器人的最高点 F距地面 AB的高度约
为 cm。(参考数据: sin80 0.98, cos80 ≈0.17, tan80 ≈5.67)
18.如图,∠MON=30°,在 OM上截取OA1 3,过点 A1作 A1B1⊥OM,交 ON于点 B1,以点 B1为圆心,
B1O为半径画弧,交 OM于点 A2;过点 A2作 A2B2⊥OM,交 ON于点 B2,以点 B2为圆心,B2O为半径画弧,
交 OM于点 A3……按此规律;所得线段 A2024B2024=_______。
(第 16 题图) (第 17 题图) (第 18 题图)
九年级数学试题 第 3 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
三、解答题(本题共 7 个小题,共 62 分。解答题要写出必要的文字说明、证明过程或演算步骤)
19.(每小题 4分,共 8分)
1
-1
(1)计算: 12 - tan60 - - 2cos30 -1 (cos60 - 2024)0
2
2
(2)先化简,再求值: 1 1 x 4 ,其中 x 3tan30 2
x 1 x 1
20.(第 1 小题 1 分,第 2 小题 2 分,第 3 小题 1 分,第 4 小题 4 分,共 8 分)
为了解中考体育科目训练情况,某区从九年级学生中抽取了部分学生进行了一次中考体育科测试(把测试
结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两
幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)求本次抽样测试的学生人数;
(2)求图 1 中 的度数,并把图 2 条形统计图补充完整;
(3)该区九年级有学生 4000名,如果全部参加这次体育测试,请估计不及格的人数大约是多少;
(4)测试老师想从 4 位同学(分别记为甲、乙、丙、丁,其中甲为小明)中随机选择两位同学了解平时
训练情况,请用列表或画树状图的方法求出选中小明的概率。
21.(每小题 4分,共 8分)
小莹妈妈的花卉超市以 15 元/盆的价格新购进了某种盆栽花卉,为了确定售价,小莹帮妈妈调查了附近 A,
B,C,D,E五家花卉店近期该种盆栽花卉的售价与日销售量情况,并记录如下:
售价 x(元/盒) 18 20 22 26 30
日销售量 y(盒) 54 50 46 38 30
(1)分析表格中数据的变化规律,求日销售量 y与售价 x之间的关系式;
(2)根据以上信息,售价定为多少时,小莹妈妈在销售该种花卉中每天能够获得最大利润?
九年级数学试题 第 4 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
22.(第 1小题 3分,第 3小题 3分,第 3小题 2分,共 8分)
k
如图,在 ABCD中,顶点 A的坐标是 0,1 。AD∥x轴,一次函数 y x 1与反比例函数 y 的图象都经
x
过 B( 1,a)、D两点。
(1)求 k,a的值;
(2)求平行四边形 ABCD的面积;
k
(3)根据图象,直接写出不等式 x 1 的解集。
x
(第 22 题图)
23.(每小题 4分,共 8分)
如图,在△ABC中,O是 AC上(异于点 A,C)的一点,⊙O恰好经过点 A,B,AD CB于点 D,且 AB
平分 CAD。
(1)判断 BC与⊙O的位置关系,并说明理由;
(2)若 AD=6,DC 8,求⊙O的半径长。
(第 23 题图)
九年级数学试题 第 5 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
24.(第 1小题 2分,第 2小题 4分,第 3小题 6 分,共 12分)
如图,抛物线 y x2 bx c与 x 轴交于 A,B(3,0)两点,与 y轴交于点 C(0,3)。
(1)求抛物线的表达式;
(2)如图①,M是 x轴上方抛物线上一点,过点 M作 MH∥y轴,交 x轴与点 H,若 MN=BN,
sin NBH 4且 ,请写出点 M的坐标;
5
(3)如图②,点 D在线段 BC上,且 CD=BD,点 E是直线 BC上方抛物线上一点,连接 BE,DE,
此时△BDE面积是否存在最大值?若存在,请求出其最大面积并写出此时点 E的坐标;若不存在,请说明
理由。
(第 24 题图① ) (第 24 题图②)
25.(第 1 小题 3分,第 2 小题 3分,第 3 小题 4分,共 10分)
如图 B,E,C,F共线,EF为半圆 O的直径,△ABC为等边三角形,点 B与点 F重合,BC=EF=4,现将半圆
O沿直线 l 以每秒 1 个单位长度的速度向右移动,当半圆 O与 AB相交时,交点为 P,运动时间为 t秒。
(1)过点 A作半圆 O的切线,切点为 Q,当 t=2 时,求 E Q的长;
(2)如图②,连接 PE,当∠PEF=15°时,求 PB的值;
(3)如图③,当△OBP为等腰三角形时,求 t的值。
(第 25 题图① ) (第 25 题图② ) (第 25 题图③)
九年级数学试题 第 6 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
九年级数学试题
(总分 120 分,考试时间 120 分钟)
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分,第一卷为选择题,30分;第二卷为非选择题,90分;本试题共 6页。
2.数学试题答题卡共 4页,答题前,考生务必将自己的姓名、班级、学校、准考证号等填写在试题和答题
卡上。
3. 第Ⅰ卷每题选出答案后,都必须用 2B 铅笔把答题卡上对应题目的答案标号【ABCD】涂黑。如需改动,
先用橡皮擦干净,再涂改其它答案。第二卷按要求用 0.5mm碳素笔答在答题卡的相应位置上。
第Ⅰ卷(选择题 共 30分)
一、选择题(本题共 10个小题,每小题 3分,共 30分)
1.化学实验室中竖直放置的玻璃漏斗,其主视图是( )
A. B. C. D.
2.二次函数 y x2 2x 2的图象的对称轴是( )
A. x= 1 B. x 2 C. x 1 D. x 2
3.一个正多边形的中心角为30 ,这个正多边形的边数是( )
A.8 B.12 C.3 D.6
4.如图,在△ABC中, C 90 , B 42 , BC 8,若用科学计算器求 AC的长,则下列按键顺序正
确的是( )
A. 8 sin 4 2 B. 8 cos 4 2 C. 8 tan 4 2 D. 8 tan 4 2
(第 4 题图) (第 5 题图)
5.如图,AB为 O的直径,C,D为⊙O上的两点,若 ABD=54 ,则 C的度数为( )
A.34 B.36 C. 46 D.54
6.从下面四个图形中任意选取一个图形,所选图形既是中心对称图形,又是轴对称图形的概率是( )
A. 1 B. 1 C. 3 D.1
4 2 4
九年级数学试题 第 1 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
7.中国廊桥是桥梁与房屋的珠联璧合,代表着中国人的智慧和造艺,是世界文明宝库的一大奇观。如图,
1 2
这是某座下方为抛物线形的廊桥示意图,已知抛物线的表达式为 y x 12,为保护廊桥的安全,在
40
该抛物线上距水面 AB高为 8 米的点 E,F处要安装两盏警示灯,则这两盏灯的水平距离 EF长为( )
A.8 10米 B.16 米 C.8 5米 D.16 2米
c
8.若二次函数 y ax2 bx c(a 0)的图象如图所示,则一次函数 y ax b与反比例函数 y 在同一个
x
坐标系内的大致图象为( )
9.如图,△ABC的顶点 A,C分别落在表盘外边框的10时和 4时位置上 .已知 ACB 90 , AB与表盘的
外边框交于点D( 2时位置)若 BD 1,则表盘直径的长度为( )
A. 4 B. 2 3 C. 2 D. 3
10.函数 y ax2 bx c a 0,b2 4ac 0 y ax2 2的图象是由函数 bx c a 0,b 4ac 0 的图象 x轴
上方部分不变, x轴下方部分沿 x轴向上翻折而成,如图所示,则下列结论正确的是( )
① 2a b 0 ;② c 3; ③ abc 0;④3a+c=0;⑤将图象向上平移 1 个单位后与直线 y 5有 3 个交点.
A.①②③ B.①④⑤ C.①②③④ D.①③④⑤
(第 9题图) (第 10 题图)
九年级数学试题 第 2 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
第Ⅱ卷(非选择题 共 90 分)
二、填空题(本题共 8 个小题,其中 11-14 题每小题 3 分,15-18 题每小题 4 分,共 28 分,只要求填写
最后结果)
11.抛物线 y 3 x 2 2 4的顶点坐标是 。
2
12. 1 己知△ABC中, A , B都是锐角,且 cos A | tan B 3 | 0,则 C 度。
2
13.如图,圆锥的左视图是边长为 2的等边三角形,则此圆锥的高是________________。
14.如图,一扇形纸扇完全打开后,外侧两竹条 AB和 AC的夹角为 120°,AB长为 30cm,贴纸部分的宽
BD为 20cm,则贴纸部分的面积为________cm2(纸扇有两面,结果保留π)。
k
15.如图,反比例函数 y 的图象上有一点 P,PA⊥x轴于点 A,点 B在 y轴上,△PAB的面积为 1,则
x
k=_______。
(第 13 题图) (第 14 题图) (第 15 题图)
16.中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”。“方田一段,一
角圆池占之。”意思是说:“一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均
相切)”,如图所示。
问题:若正方形的边长为 10 丈,⊙O的半径为 2 丈,则点 D到⊙O的最短距离为____丈。
17.近年来,随着智能技术的发展,智能机器人已经服务于社会生活的各个方面.图 1所示是一款智能送货
机器人,图 2是其侧面示意图,现测得其矩形底座 ABCD的高 BC为30cm,上部显示屏 EF的长度为30cm,
侧面支架 EC的长度为100cm, ECD 80 , FEC 130 ,则该机器人的最高点 F距地面 AB的高度约
为 cm。(参考数据: sin80 0.98, cos80 ≈0.17, tan80 ≈5.67)
18.如图,∠MON=30°,在 OM上截取OA1 3,过点 A1作 A1B1⊥OM,交 ON于点 B1,以点 B1为圆心,
B1O为半径画弧,交 OM于点 A2;过点 A2作 A2B2⊥OM,交 ON于点 B2,以点 B2为圆心,B2O为半径画弧,
交 OM于点 A3……按此规律;所得线段 A2024B2024=_______。
(第 16 题图) (第 17 题图) (第 18 题图)
九年级数学试题 第 3 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
三、解答题(本题共 7 个小题,共 62 分。解答题要写出必要的文字说明、证明过程或演算步骤)
19.(每小题 4分,共 8分)
1
-1
(1)计算: 12 - tan60 - - 2cos30 -1 (cos60 - 2024)0
2
2
(2)先化简,再求值: 1 1 x 4 ,其中 x 3tan30 2
x 1 x 1
20.(第 1 小题 1 分,第 2 小题 2 分,第 3 小题 1 分,第 4 小题 4 分,共 8 分)
为了解中考体育科目训练情况,某区从九年级学生中抽取了部分学生进行了一次中考体育科测试(把测试
结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两
幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)求本次抽样测试的学生人数;
(2)求图 1 中 的度数,并把图 2 条形统计图补充完整;
(3)该区九年级有学生 4000名,如果全部参加这次体育测试,请估计不及格的人数大约是多少;
(4)测试老师想从 4 位同学(分别记为甲、乙、丙、丁,其中甲为小明)中随机选择两位同学了解平时
训练情况,请用列表或画树状图的方法求出选中小明的概率。
21.(每小题 4分,共 8分)
小莹妈妈的花卉超市以 15 元/盆的价格新购进了某种盆栽花卉,为了确定售价,小莹帮妈妈调查了附近 A,
B,C,D,E五家花卉店近期该种盆栽花卉的售价与日销售量情况,并记录如下:
售价 x(元/盒) 18 20 22 26 30
日销售量 y(盒) 54 50 46 38 30
(1)分析表格中数据的变化规律,求日销售量 y与售价 x之间的关系式;
(2)根据以上信息,售价定为多少时,小莹妈妈在销售该种花卉中每天能够获得最大利润?
九年级数学试题 第 4 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
22.(第 1小题 3分,第 3小题 3分,第 3小题 2分,共 8分)
k
如图,在 ABCD中,顶点 A的坐标是 0,1 。AD∥x轴,一次函数 y x 1与反比例函数 y 的图象都经
x
过 B( 1,a)、D两点。
(1)求 k,a的值;
(2)求平行四边形 ABCD的面积;
k
(3)根据图象,直接写出不等式 x 1 的解集。
x
(第 22 题图)
23.(每小题 4分,共 8分)
如图,在△ABC中,O是 AC上(异于点 A,C)的一点,⊙O恰好经过点 A,B,AD CB于点 D,且 AB
平分 CAD。
(1)判断 BC与⊙O的位置关系,并说明理由;
(2)若 AD=6,DC 8,求⊙O的半径长。
(第 23 题图)
九年级数学试题 第 5 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
24.(第 1小题 2分,第 2小题 4分,第 3小题 6 分,共 12分)
如图,抛物线 y x2 bx c与 x 轴交于 A,B(3,0)两点,与 y轴交于点 C(0,3)。
(1)求抛物线的表达式;
(2)如图①,M是 x轴上方抛物线上一点,过点 M作 MH∥y轴,交 x轴与点 H,若 MN=BN,
sin NBH 4且 ,请写出点 M的坐标;
5
(3)如图②,点 D在线段 BC上,且 CD=BD,点 E是直线 BC上方抛物线上一点,连接 BE,DE,
此时△BDE面积是否存在最大值?若存在,请求出其最大面积并写出此时点 E的坐标;若不存在,请说明
理由。
(第 24 题图① ) (第 24 题图②)
25.(第 1 小题 3分,第 2 小题 3分,第 3 小题 4分,共 10分)
如图 B,E,C,F共线,EF为半圆 O的直径,△ABC为等边三角形,点 B与点 F重合,BC=EF=4,现将半圆
O沿直线 l 以每秒 1 个单位长度的速度向右移动,当半圆 O与 AB相交时,交点为 P,运动时间为 t秒。
(1)过点 A作半圆 O的切线,切点为 Q,当 t=2 时,求 E Q的长;
(2)如图②,连接 PE,当∠PEF=15°时,求 PB的值;
(3)如图③,当△OBP为等腰三角形时,求 t的值。
(第 25 题图① ) (第 25 题图② ) (第 25 题图③)
九年级数学试题 第 6 页 共 6 页
{#{QQABLYSUogioAAAAAQgCEwGoCEAQkAGAACoGxAAAIAAByBFABAA=}#}
同课章节目录
