甘肃省兰州市重点中学2023—2024学年七年级下学期开学测试数学试卷(含解析)
文档属性
| 名称 | 甘肃省兰州市重点中学2023—2024学年七年级下学期开学测试数学试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 882.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 20:51:05 | ||
图片预览




文档简介
2024年寒假作业检测卷
七年级数学
一.选择题(共10小题,满分30分,每小题3分)
1.的相反数是( )
A.2024 B.﹣2024 C. D.
2.2023年5月21日,以“聚力新南通、奋进新时代”为主题的第五届通商大会暨全市民营经济发展大会召开,40个重大项目集中签约,计划总投资约41800000000元,将41800000000用科学记数法表示为( )
A.4.18×1011 B.4.18×1010 C.0.418×1011 D.418×108
3.下列说法中正确的是( )
A.正方体和长方体是特殊的四棱柱,也是特殊的六面体 B.棱柱底面边数和侧面数不一定相等
C.棱柱的侧面可能是三角形 D.长方体是四棱柱,四棱柱是长方体
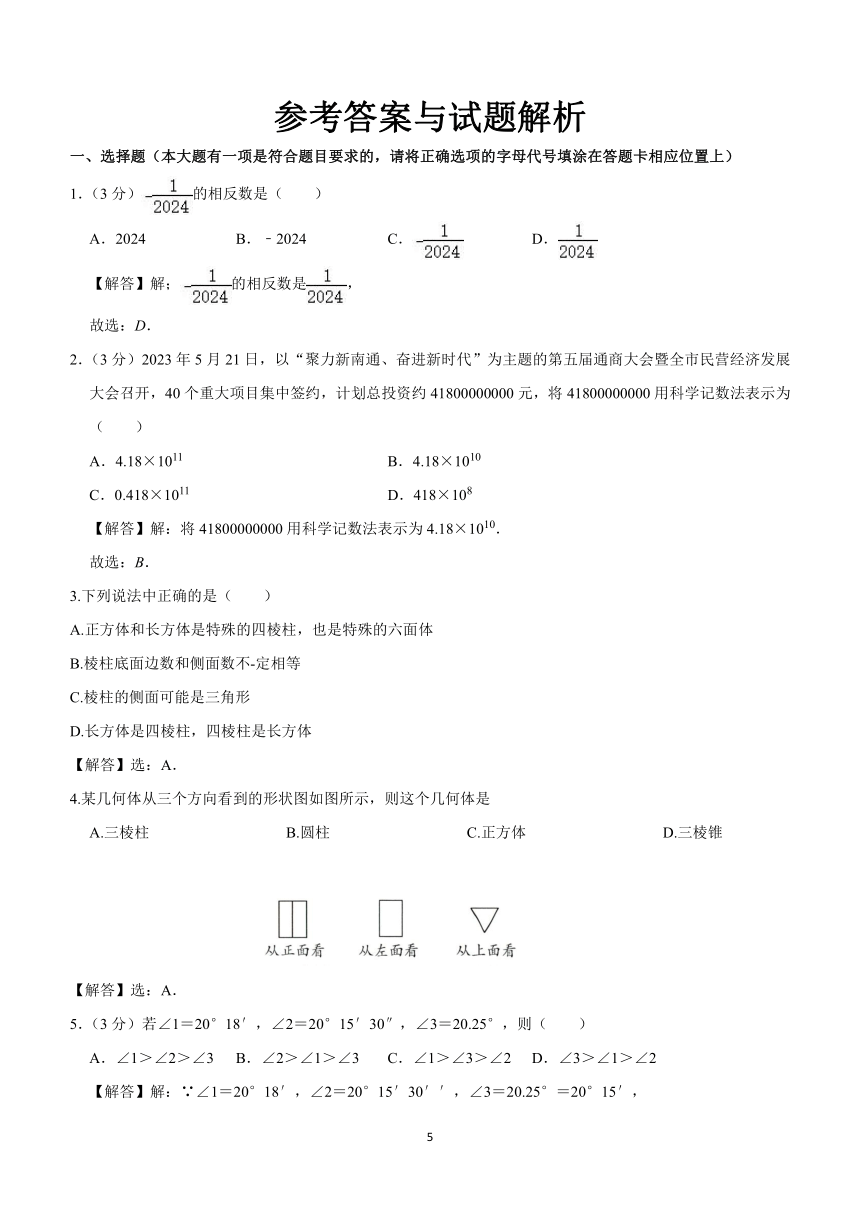
4.某几何体从三个方向看到的形状图如图所示,则这个几何体是( )
A.三棱柱 B.圆柱
C.正方体 D.三棱锥
5.若∠1=20°18′,∠2=20°15′30″,∠3=20.25°,则( )
A.∠1>∠2>∠3 B.∠2>∠1>∠3 C.∠1>∠3>∠2 D.∠3>∠1>∠2
6.去年某市有5.6万名学生参加联招考试,为了了解他们的数学成绩,从中抽取2 000名考生的数学成绩进行统计分析,下列说法错误的是( )
A.个体是每名考生的数学成绩 B.5.6万名学生是总体
C.2 000是样本容量 D.2 0000名考生的数学成绩是总体的一个样本
7.某商场促销,把原价2500元的空调以八折出售,仍可获利400元,则这款空调进价为( )
A.1600元 B.1500元 C.1375元 D.2000元
8.下列说法正确的是( )
A.两点之间,直线最短 B.多项式7xy3 +2xy +5的次数为3
C.六棱柱有8个面 D.“a 与b的和的3倍”可表示为a+ 3b
9.若一个多边形从一个顶点最多能引出5条对角线,则这个多边形是( )
A.六边形 B.八边形 C.九边形 D.十边形
10.数学兴趣小组的一位同学用棋子摆图形探究规律如图所示,若按照他的规律继续摆下去,第n个图案中用了2 025颊棋子,则n的值为( )
A.506 B.507 C.508 D.509
二.填空题(共4小题,满分12分,每小题3分)
11.若.则的值是 .
12.如图,D是AB的中点,AC:CB=2:3且CD=9,则AB的长为 .
13.单项式与是同类项,则m= ,n= .
14.a,b,c在数轴上的位置如图所示,则 .
三.解答题(共12小题,满分58分)
15.计算:
(1); (2).
16.解方程:
(1)2(x+3)=3(x﹣2); (2)
17. 先化简,再求值:,其中a,b满足
18.如图,已知线段a,b,利用尺规作图法求作线段MN,使得MN=b-2a. (不写作法,保留作图痕迹)
19.如图所示,已知直线AB,CD相交于点O,且∠DOE=∠BOD,OM平分∠AOE,若∠AOC= 32°,求∠EOM的度数.
20.为了提高学生书写汉字的能力增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生同时听写50个汉字,若每正确听写出一一个汉字得1分根据测试成绩(每位同学成绩都不低于25分)绘制出部分顿数统计表和部分频数直方图如下:
请结合以上图表完成下列各题:
(1)求表中a的值;
(2)请把频数直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
21.某自行车厂计划一周生产1 400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出人,下表是某周的生产情况(超产为正,减产为负,单位:辆).
(1)产量最多的一天比产量最少的一天多生产多少辆
(2)该厂实行计件工资制度,每辆车60元,一周结束超额完成任务时,超出部分每辆车奖15元,少生产一辆扣10元,那么该厂工人这一周的工资总额是多少
22.佳佳平价商场经销的甲、乙两种商品,甲种商品每件售价70元,利润率为40%;乙种商品每件进价40元,售价60元.
(1)甲种商品每件进价为_______元,每件乙种商品利润率为_______;
(2)在“春节”前夕,该商场只对甲种商品进行如下的优惠促销活动:
按上述优惠条件,若顾客小贺一次性购买甲种商品实际付款630元,求小贺在该商场购买甲种商品多少件
23.如图,数轴上线段AB=2 (单位长度),线段CD=4 (单位长度),点A在数轴上表示的数是-12,点C在数轴上表示的数是14. 若线段AB以每秒2个单位长度的速度向右匀速运动,同时线段CD以每秒1个单位长度的速度向左匀速运动. 设运动时间为t s.
(1)当点B与点C相遇时,点A、D在数轴上表示的数分别是 、 .
(2)当t为何值时,点B刚好与线段CD的中点重合;
(3)当运动到BC=9 (单位长度)时,求出此时点B在数轴上表示的数.
24.如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面. 请观察各图形并解答有关问题:
(1)在第n个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含n的代数式表示);
(2)设铺设地面所用瓷砖的总块数为y,用(1)中的n表示y;
(3)当n=20时,求y的值;
(4)若黑瓷砖每块4元,白瓷砖每块3元,在问题(3)中,共需花多少元购买瓷砖
参考答案与试题解析
一、选择题(本大题有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.(3分)的相反数是( )
A.2024 B.﹣2024 C. D.
【解答】解;的相反数是,
故选:D.
2.(3分)2023年5月21日,以“聚力新南通、奋进新时代”为主题的第五届通商大会暨全市民营经济发展大会召开,40个重大项目集中签约,计划总投资约41800000000元,将41800000000用科学记数法表示为( )
A.4.18×1011 B.4.18×1010
C.0.418×1011 D.418×108
【解答】解:将41800000000用科学记数法表示为4.18×1010.
故选:B.
3.下列说法中正确的是( )
A.正方体和长方体是特殊的四棱柱,也是特殊的六面体
B.棱柱底面边数和侧面数不-定相等
C.棱柱的侧面可能是三角形
D.长方体是四棱柱,四棱柱是长方体
【解答】选:A.
4.某几何体从三个方向看到的形状图如图所示,则这个几何体是
A.三棱柱 B.圆柱 C.正方体 D.三棱锥
【解答】选:A.
5.(3分)若∠1=20°18′,∠2=20°15′30″,∠3=20.25°,则( )
A.∠1>∠2>∠3 B.∠2>∠1>∠3 C.∠1>∠3>∠2 D.∠3>∠1>∠2
【解答】解:∵∠1=20°18′,∠2=20°15′30′′,∠3=20.25°=20°15′,
∴∠1>∠2>∠3.
故选:A.
6.去年某市有5.6万名学生参加联招考试,为了了解他们的数学成绩,从中抽取2 000名考生的数学成绩进行统计分析,下列说法错误的是( )
A.个体是每名考生的数学成绩
B.5.6万名学生是总体
C.2 000是样本容量
D.2 0000名考生的数学成绩是总体的一一个样本
【解答】选:B.
7.(3分)某商场促销,把原价2500元的空调以八折出售,仍可获利400元,则这款空调进价为( )
A.1600元 B.1500元 C.1375元 D.2000元
【解答】解:设这款空调进价为x元,
则x+400=2500×80%,
∴x+400=2000,
解得:x=1600.
答:这款空调进价为1600元.
故选:A.
8.下列说法正确的是( )
A.两点之间,直线最短 B.多项式7xy3 +2xy +5的次数为3
C.六棱柱有8个面 D.“a 与b的和的3倍”可表示为a+ 3b
【解答】选:C.
9.若一个多边形从一个顶点最多能引出5条对角线,则这个多边形是( )
A.六边形 B.八边形 C.九边形 D.十边形
【解答】选:B.
10.数学兴趣小组的一位同学用棋子摆图形探究规律如图所示,若按照他的规律继续摆下去,第n个图案中用了2 025颊棋子,则n的值为( )
A.506 B.507 C.508 D.509
【解答】选:A.
二、填空题(本大题共8小题,第11~12题每小题3分,第13~18题每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
11.若.则的值是 .
【解答】解:答案为:
12.(4分)如图,D是AB的中点,AC:CB=2:3且CD=9,则AB的长为 90 .
【解答】解:答案为:90.
单项式与是同类项,则m= ,n= .
【解答】解: 答案为:m=7或-3,n=15.
a,b,c在数轴上的位置如图所示,则 .
【解答】解: 答案: 0.
三、解答题
15.计算:
(1)÷4;
(2).
【解答】解:
(1)÷4
=÷(﹣)﹣×﹣×
=×(﹣)﹣×﹣
=﹣×﹣×﹣
=×(﹣﹣﹣1)
=×(﹣)
=﹣;
(2)
=﹣36×+36×﹣36×
=﹣27+42﹣33
=15﹣33
=﹣18.
16.解方程:
(1)2(x+3)=3(x﹣2);
(2)=2.
【解答】解:(1)2(x+3)=3(x﹣2),
去括号,得2x+6=3x﹣6,
移项,得2x﹣3x=﹣6﹣6,
合并同类项,得﹣x=﹣12,
系数化成1,得x=12;
(2)=2,
去分母,得3x﹣(9x﹣2)=12,
去括号,得3x﹣9x+2=12,
移项,得3x﹣9x=12﹣2,
合并同类项,得﹣6x=10,
系数化成1,得x=﹣.
17.先化简,再求值:,其中a,b满足
【解答】
18.如图,已知线段a,b,利用尺规作图法求作线段MN,使得MN=b-2a. (不写作法,保留作图痕迹)
【解答】
19.如图所示,已知直线AB,CD相交于点O,且∠DOE=∠BOD,OM平分∠AOE,若∠AOC= 32°,求∠EOM的度数.
【解答】
因为直线AB、CD交于点O
所以∠BOD与∠AOC是对顶角,
所以∠BOD=∠ AOC= 30°.
又因为∠DOE=∠BOD,
所以∠BOE=∠BOD+∠DOE=60°。
所以∠ AOE= 180°- ∠BOE= 180°一60°= 120°
因为OM平分∠AOE,
所以∠EOM=∠AOE=X 120°= 60°.
20.为了提高学生书写汉字的能力增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生同时听写50个汉字,若每正确听写出一一个汉字得1分根据测试成绩(每位同学成绩都不低于25分)绘制出部分顿数统计表和部分频数直方图如下:
请结合以上图表完成下列各题:
(1)求表中a的值;
(2)请把频数直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
【解答】
a=50一4一8一16一10= 12.
补全频数直方图如图所示.
(3)由频数直方图可知,不低于40分的学生有12+10=22(人),
所以本次测试的优秀率为
21.某自行车厂计划一周生产1 400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出人,下表是某周的生产情况(超产为正,减产为负,单位:辆).
(1)产量最多的一天比产量最少的一天多生产多少辆
(2)该厂实行计件工资制度,每辆车60元,一周结束超额完成任务时,超出部分每辆车奖15元,少生产一辆扣10元,那么该厂工人这一周的工资总额是多少
【解答】
(1)( +16)-( -10) =26(辆).
所以产量最多的一天比产量最少的一天多生产26辆.
(2)( +5)+(-2)+( -4)+( +13) +( -10) +( +16) +( -9) =9(辆) ,
所以这一周实际共生产自行车1400 +9=1 409(辆).
故该厂工人这一周的工资总额为1 409x60+9x15 =84 675(元).
22.佳佳平价商场经销的甲、乙两种商品,甲种商品每件售价70元,利润率为40%;乙种商品每件进价40元,售价60元.
(1)甲种商品每件进价为_______元,每件乙种商品利润率为_______;
(2)在“春节”前夕,该商场只对甲种商品进行如下的优惠促销活动:
按上述优惠条件,若顾客小贺一次性购买甲种商品实际付款630元,求小贺在该商场购买甲种商品多少件
【解答】
(1)解:设甲种商品的进价为a元,
则
解得a= 50,
即甲种商品每件进价为50元,
即每件乙种商品利润率为50%,
故答案是: 50; 50%;
(2)解:设小贺在该商场购买甲种商品b件,
①当购物金额超过560元,但不超过700元时,
70b0.9= 630,
解得: b=10;
②当购物金额超过700元时,
7008.7 +(70b- 700)0.3= 630
解得: b=11.
答:小贺在该商场购买甲种商品10或11件.
23.如图,数轴上线段AB=2 (单位长度),线段CD=4 (单位长度),点A在数轴上表示的数是-12,点C在数轴上表示的数是14.若线段AB以每秒2个单位长度的速度向右匀速运动,同时线段CD以每秒1个单位长度的速度向左匀速运动.设运动时间为t s.
(1)当点B与点C相遇时,点A、D在数轴上表示的数分别是 、 .
(2)当t为何值时,点B刚好与线段CD的中点重合;
(3)当运动到BC=9 (单位长度)时,求出此时点B在数轴上表示的数.
【解答】
(1) 4; 10
(2)由题意得B表示的数是-10, 线段CD的中点
在数轴上表示的数是16,
(2+ 1)t= 16-(-10),t=
答: t=时,点B刚好与线段CD的中点重合。
(3)①B在C的左侧时,
(2+ 1)t+9= 14-(-10), t= 5
-10+ 25= 0
②B在C的右侧时,
(2+ 1)t= 14- (-10)+ 9, t=11,
-10+211 = 12
所以点B在数轴上表示的数是0或12。
24.如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面.请观察各图形并解答有关问题:
(1)在第n个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含n的代数式表示);
(2)设铺设地面所用瓷砖的总块数为y,用(1)中的n表示y;
(3)当n=20时,求y的值;
(4)若黑瓷砖每块4元,白瓷砖每块3元,在问题(3)中,共需花多少元购买瓷砖
【解答】
解:(1)n+3、n+2
(2)y=(n+3)(n+2).
(3)当n=20时,y=(20+3)(20+2)=506.
(4)由题图可知,第n个图形中黑瓷砖有[(n+3)(n+2)-n(n+1)]块,白瓷砖有n(n+1)块.
当n=20时,黑瓷砖有86块,白瓷砖有420块,所以共需花864 +4203=1604(元).
答:共需花1 604元购买瓷砖.
七年级数学
一.选择题(共10小题,满分30分,每小题3分)
1.的相反数是( )
A.2024 B.﹣2024 C. D.
2.2023年5月21日,以“聚力新南通、奋进新时代”为主题的第五届通商大会暨全市民营经济发展大会召开,40个重大项目集中签约,计划总投资约41800000000元,将41800000000用科学记数法表示为( )
A.4.18×1011 B.4.18×1010 C.0.418×1011 D.418×108
3.下列说法中正确的是( )
A.正方体和长方体是特殊的四棱柱,也是特殊的六面体 B.棱柱底面边数和侧面数不一定相等
C.棱柱的侧面可能是三角形 D.长方体是四棱柱,四棱柱是长方体
4.某几何体从三个方向看到的形状图如图所示,则这个几何体是( )
A.三棱柱 B.圆柱
C.正方体 D.三棱锥
5.若∠1=20°18′,∠2=20°15′30″,∠3=20.25°,则( )
A.∠1>∠2>∠3 B.∠2>∠1>∠3 C.∠1>∠3>∠2 D.∠3>∠1>∠2
6.去年某市有5.6万名学生参加联招考试,为了了解他们的数学成绩,从中抽取2 000名考生的数学成绩进行统计分析,下列说法错误的是( )
A.个体是每名考生的数学成绩 B.5.6万名学生是总体
C.2 000是样本容量 D.2 0000名考生的数学成绩是总体的一个样本
7.某商场促销,把原价2500元的空调以八折出售,仍可获利400元,则这款空调进价为( )
A.1600元 B.1500元 C.1375元 D.2000元
8.下列说法正确的是( )
A.两点之间,直线最短 B.多项式7xy3 +2xy +5的次数为3
C.六棱柱有8个面 D.“a 与b的和的3倍”可表示为a+ 3b
9.若一个多边形从一个顶点最多能引出5条对角线,则这个多边形是( )
A.六边形 B.八边形 C.九边形 D.十边形
10.数学兴趣小组的一位同学用棋子摆图形探究规律如图所示,若按照他的规律继续摆下去,第n个图案中用了2 025颊棋子,则n的值为( )
A.506 B.507 C.508 D.509
二.填空题(共4小题,满分12分,每小题3分)
11.若.则的值是 .
12.如图,D是AB的中点,AC:CB=2:3且CD=9,则AB的长为 .
13.单项式与是同类项,则m= ,n= .
14.a,b,c在数轴上的位置如图所示,则 .
三.解答题(共12小题,满分58分)
15.计算:
(1); (2).
16.解方程:
(1)2(x+3)=3(x﹣2); (2)
17. 先化简,再求值:,其中a,b满足
18.如图,已知线段a,b,利用尺规作图法求作线段MN,使得MN=b-2a. (不写作法,保留作图痕迹)
19.如图所示,已知直线AB,CD相交于点O,且∠DOE=∠BOD,OM平分∠AOE,若∠AOC= 32°,求∠EOM的度数.
20.为了提高学生书写汉字的能力增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生同时听写50个汉字,若每正确听写出一一个汉字得1分根据测试成绩(每位同学成绩都不低于25分)绘制出部分顿数统计表和部分频数直方图如下:
请结合以上图表完成下列各题:
(1)求表中a的值;
(2)请把频数直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
21.某自行车厂计划一周生产1 400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出人,下表是某周的生产情况(超产为正,减产为负,单位:辆).
(1)产量最多的一天比产量最少的一天多生产多少辆
(2)该厂实行计件工资制度,每辆车60元,一周结束超额完成任务时,超出部分每辆车奖15元,少生产一辆扣10元,那么该厂工人这一周的工资总额是多少
22.佳佳平价商场经销的甲、乙两种商品,甲种商品每件售价70元,利润率为40%;乙种商品每件进价40元,售价60元.
(1)甲种商品每件进价为_______元,每件乙种商品利润率为_______;
(2)在“春节”前夕,该商场只对甲种商品进行如下的优惠促销活动:
按上述优惠条件,若顾客小贺一次性购买甲种商品实际付款630元,求小贺在该商场购买甲种商品多少件
23.如图,数轴上线段AB=2 (单位长度),线段CD=4 (单位长度),点A在数轴上表示的数是-12,点C在数轴上表示的数是14. 若线段AB以每秒2个单位长度的速度向右匀速运动,同时线段CD以每秒1个单位长度的速度向左匀速运动. 设运动时间为t s.
(1)当点B与点C相遇时,点A、D在数轴上表示的数分别是 、 .
(2)当t为何值时,点B刚好与线段CD的中点重合;
(3)当运动到BC=9 (单位长度)时,求出此时点B在数轴上表示的数.
24.如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面. 请观察各图形并解答有关问题:
(1)在第n个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含n的代数式表示);
(2)设铺设地面所用瓷砖的总块数为y,用(1)中的n表示y;
(3)当n=20时,求y的值;
(4)若黑瓷砖每块4元,白瓷砖每块3元,在问题(3)中,共需花多少元购买瓷砖
参考答案与试题解析
一、选择题(本大题有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.(3分)的相反数是( )
A.2024 B.﹣2024 C. D.
【解答】解;的相反数是,
故选:D.
2.(3分)2023年5月21日,以“聚力新南通、奋进新时代”为主题的第五届通商大会暨全市民营经济发展大会召开,40个重大项目集中签约,计划总投资约41800000000元,将41800000000用科学记数法表示为( )
A.4.18×1011 B.4.18×1010
C.0.418×1011 D.418×108
【解答】解:将41800000000用科学记数法表示为4.18×1010.
故选:B.
3.下列说法中正确的是( )
A.正方体和长方体是特殊的四棱柱,也是特殊的六面体
B.棱柱底面边数和侧面数不-定相等
C.棱柱的侧面可能是三角形
D.长方体是四棱柱,四棱柱是长方体
【解答】选:A.
4.某几何体从三个方向看到的形状图如图所示,则这个几何体是
A.三棱柱 B.圆柱 C.正方体 D.三棱锥
【解答】选:A.
5.(3分)若∠1=20°18′,∠2=20°15′30″,∠3=20.25°,则( )
A.∠1>∠2>∠3 B.∠2>∠1>∠3 C.∠1>∠3>∠2 D.∠3>∠1>∠2
【解答】解:∵∠1=20°18′,∠2=20°15′30′′,∠3=20.25°=20°15′,
∴∠1>∠2>∠3.
故选:A.
6.去年某市有5.6万名学生参加联招考试,为了了解他们的数学成绩,从中抽取2 000名考生的数学成绩进行统计分析,下列说法错误的是( )
A.个体是每名考生的数学成绩
B.5.6万名学生是总体
C.2 000是样本容量
D.2 0000名考生的数学成绩是总体的一一个样本
【解答】选:B.
7.(3分)某商场促销,把原价2500元的空调以八折出售,仍可获利400元,则这款空调进价为( )
A.1600元 B.1500元 C.1375元 D.2000元
【解答】解:设这款空调进价为x元,
则x+400=2500×80%,
∴x+400=2000,
解得:x=1600.
答:这款空调进价为1600元.
故选:A.
8.下列说法正确的是( )
A.两点之间,直线最短 B.多项式7xy3 +2xy +5的次数为3
C.六棱柱有8个面 D.“a 与b的和的3倍”可表示为a+ 3b
【解答】选:C.
9.若一个多边形从一个顶点最多能引出5条对角线,则这个多边形是( )
A.六边形 B.八边形 C.九边形 D.十边形
【解答】选:B.
10.数学兴趣小组的一位同学用棋子摆图形探究规律如图所示,若按照他的规律继续摆下去,第n个图案中用了2 025颊棋子,则n的值为( )
A.506 B.507 C.508 D.509
【解答】选:A.
二、填空题(本大题共8小题,第11~12题每小题3分,第13~18题每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
11.若.则的值是 .
【解答】解:答案为:
12.(4分)如图,D是AB的中点,AC:CB=2:3且CD=9,则AB的长为 90 .
【解答】解:答案为:90.
单项式与是同类项,则m= ,n= .
【解答】解: 答案为:m=7或-3,n=15.
a,b,c在数轴上的位置如图所示,则 .
【解答】解: 答案: 0.
三、解答题
15.计算:
(1)÷4;
(2).
【解答】解:
(1)÷4
=÷(﹣)﹣×﹣×
=×(﹣)﹣×﹣
=﹣×﹣×﹣
=×(﹣﹣﹣1)
=×(﹣)
=﹣;
(2)
=﹣36×+36×﹣36×
=﹣27+42﹣33
=15﹣33
=﹣18.
16.解方程:
(1)2(x+3)=3(x﹣2);
(2)=2.
【解答】解:(1)2(x+3)=3(x﹣2),
去括号,得2x+6=3x﹣6,
移项,得2x﹣3x=﹣6﹣6,
合并同类项,得﹣x=﹣12,
系数化成1,得x=12;
(2)=2,
去分母,得3x﹣(9x﹣2)=12,
去括号,得3x﹣9x+2=12,
移项,得3x﹣9x=12﹣2,
合并同类项,得﹣6x=10,
系数化成1,得x=﹣.
17.先化简,再求值:,其中a,b满足
【解答】
18.如图,已知线段a,b,利用尺规作图法求作线段MN,使得MN=b-2a. (不写作法,保留作图痕迹)
【解答】
19.如图所示,已知直线AB,CD相交于点O,且∠DOE=∠BOD,OM平分∠AOE,若∠AOC= 32°,求∠EOM的度数.
【解答】
因为直线AB、CD交于点O
所以∠BOD与∠AOC是对顶角,
所以∠BOD=∠ AOC= 30°.
又因为∠DOE=∠BOD,
所以∠BOE=∠BOD+∠DOE=60°。
所以∠ AOE= 180°- ∠BOE= 180°一60°= 120°
因为OM平分∠AOE,
所以∠EOM=∠AOE=X 120°= 60°.
20.为了提高学生书写汉字的能力增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生同时听写50个汉字,若每正确听写出一一个汉字得1分根据测试成绩(每位同学成绩都不低于25分)绘制出部分顿数统计表和部分频数直方图如下:
请结合以上图表完成下列各题:
(1)求表中a的值;
(2)请把频数直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
【解答】
a=50一4一8一16一10= 12.
补全频数直方图如图所示.
(3)由频数直方图可知,不低于40分的学生有12+10=22(人),
所以本次测试的优秀率为
21.某自行车厂计划一周生产1 400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出人,下表是某周的生产情况(超产为正,减产为负,单位:辆).
(1)产量最多的一天比产量最少的一天多生产多少辆
(2)该厂实行计件工资制度,每辆车60元,一周结束超额完成任务时,超出部分每辆车奖15元,少生产一辆扣10元,那么该厂工人这一周的工资总额是多少
【解答】
(1)( +16)-( -10) =26(辆).
所以产量最多的一天比产量最少的一天多生产26辆.
(2)( +5)+(-2)+( -4)+( +13) +( -10) +( +16) +( -9) =9(辆) ,
所以这一周实际共生产自行车1400 +9=1 409(辆).
故该厂工人这一周的工资总额为1 409x60+9x15 =84 675(元).
22.佳佳平价商场经销的甲、乙两种商品,甲种商品每件售价70元,利润率为40%;乙种商品每件进价40元,售价60元.
(1)甲种商品每件进价为_______元,每件乙种商品利润率为_______;
(2)在“春节”前夕,该商场只对甲种商品进行如下的优惠促销活动:
按上述优惠条件,若顾客小贺一次性购买甲种商品实际付款630元,求小贺在该商场购买甲种商品多少件
【解答】
(1)解:设甲种商品的进价为a元,
则
解得a= 50,
即甲种商品每件进价为50元,
即每件乙种商品利润率为50%,
故答案是: 50; 50%;
(2)解:设小贺在该商场购买甲种商品b件,
①当购物金额超过560元,但不超过700元时,
70b0.9= 630,
解得: b=10;
②当购物金额超过700元时,
7008.7 +(70b- 700)0.3= 630
解得: b=11.
答:小贺在该商场购买甲种商品10或11件.
23.如图,数轴上线段AB=2 (单位长度),线段CD=4 (单位长度),点A在数轴上表示的数是-12,点C在数轴上表示的数是14.若线段AB以每秒2个单位长度的速度向右匀速运动,同时线段CD以每秒1个单位长度的速度向左匀速运动.设运动时间为t s.
(1)当点B与点C相遇时,点A、D在数轴上表示的数分别是 、 .
(2)当t为何值时,点B刚好与线段CD的中点重合;
(3)当运动到BC=9 (单位长度)时,求出此时点B在数轴上表示的数.
【解答】
(1) 4; 10
(2)由题意得B表示的数是-10, 线段CD的中点
在数轴上表示的数是16,
(2+ 1)t= 16-(-10),t=
答: t=时,点B刚好与线段CD的中点重合。
(3)①B在C的左侧时,
(2+ 1)t+9= 14-(-10), t= 5
-10+ 25= 0
②B在C的右侧时,
(2+ 1)t= 14- (-10)+ 9, t=11,
-10+211 = 12
所以点B在数轴上表示的数是0或12。
24.如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面.请观察各图形并解答有关问题:
(1)在第n个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含n的代数式表示);
(2)设铺设地面所用瓷砖的总块数为y,用(1)中的n表示y;
(3)当n=20时,求y的值;
(4)若黑瓷砖每块4元,白瓷砖每块3元,在问题(3)中,共需花多少元购买瓷砖
【解答】
解:(1)n+3、n+2
(2)y=(n+3)(n+2).
(3)当n=20时,y=(20+3)(20+2)=506.
(4)由题图可知,第n个图形中黑瓷砖有[(n+3)(n+2)-n(n+1)]块,白瓷砖有n(n+1)块.
当n=20时,黑瓷砖有86块,白瓷砖有420块,所以共需花864 +4203=1604(元).
答:共需花1 604元购买瓷砖.
同课章节目录
