新课标A版必修3用样本的数字特征估计总体的数字特征
文档属性
| 名称 | 新课标A版必修3用样本的数字特征估计总体的数字特征 |  | |
| 格式 | rar | ||
| 文件大小 | 356.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-16 22:40:00 | ||
图片预览




文档简介
课件19张PPT。2.2.2用样本的数字特征估计总体的数字特征一、众数、中位数、平均数的定义1、众数 在一组数据中,出现次数最多的数据叫做这一组数据的众数。
2、中位数 将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数。练习: 某教师出了一份共3道题的测试卷,每题1分,全班得3分、2分、1分和0分的学生所占比例分别为:30%、50%、10%和10%。(1)若全班共有10人, 则平均分是多少?(2)若全班共有20人, 则平均分是多少?(3)若该班人数未知,能求出该班的平均分吗?5.画频率分布直方图复习回顾:画频率分布直方图步骤2.决定组距与组数(样本容量不超过100时,组数常分成5~12组)。 3.将数据分组(9组):
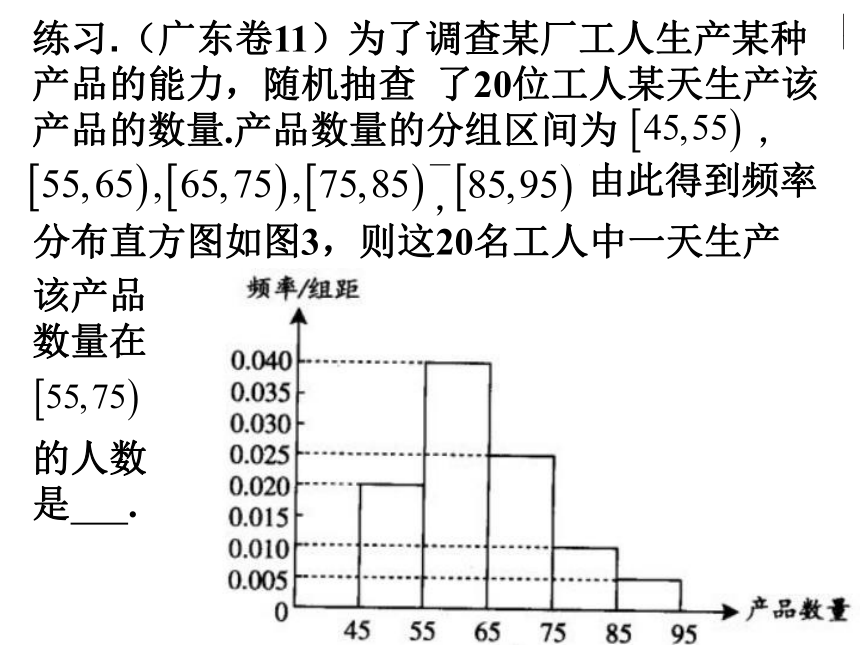
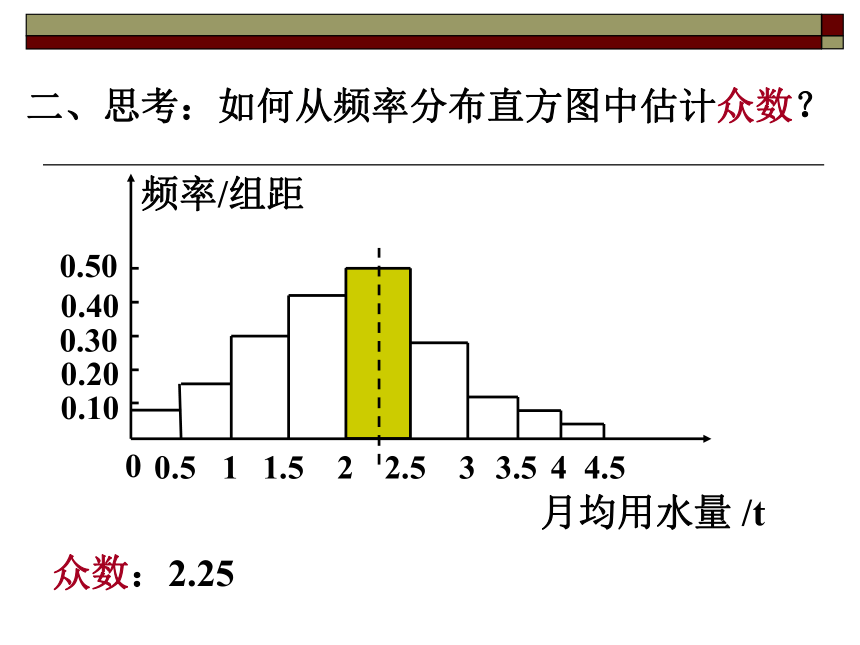
[0, 0.5) , [0.5, 1) ,~~,[4, 4.5)4.列频率分布表1.求极差(一组数据中最大值与最小值的 差)4.3-0.2=4 .1 ( t )。练习.(广东卷11)为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为,,分布直方图如图3,则这20名工人中一天生产的人数是 .该产品数量在由此得到频率二、思考:如何从频率分布直方图中估计众数?众数:2.25注:小长方形的面积=组距×频率/组距=频率
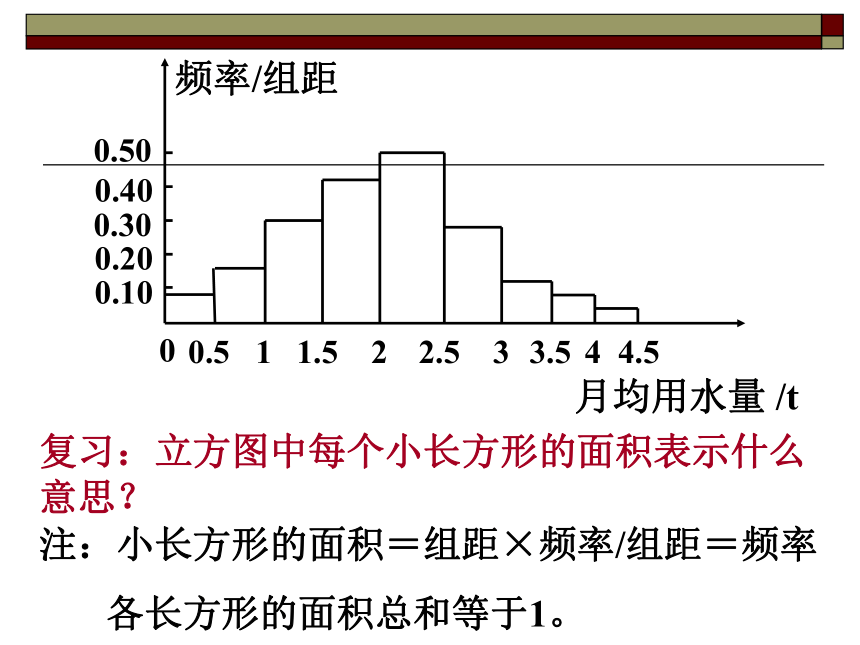
各长方形的面积总和等于1。复习:立方图中每个小长方形的面积表示什么意思?怎样从立方图中找到中位数?左边的数据个数等于右边数据的个数即左边的样本频数等于右边的样本频数个数即左边的样本频率等于右边的样本频率即立方图左、右边的小矩形的面积相等二、思考:如何从频率分布直方图中估计中位数?即中位数左边立方图的小矩形面积为0.5二、思考:如何从频率分布直方图中估计中位数?中位数左边立方图的小矩形面积为0.50~2的小矩形面积之和为:0.5×(0.8+0.16+0.30+0.44)=0.490.440.5-0.49=0.010.01/0.5=0.02如图在直线t=2.02之前所有小矩形的面积为0.5所以该样本的中位数为2.02练习.(广东11变式题1)为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为,,分布直方图如图3,则这20名工人中一天生产的中位数 .该产品数量在由此得到频率二、思考:如何从频率分布直方图中估计平均数?0.440.280.120.080.04练习.(广东11变式题2)为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为,,分布直方图如图3,则这20名工人中一天生产的平均数 .该产品数量在由此得到频率小结众数、中位数、平均数与频率分布直方图的关系:1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。2、中位数左边和右边的直方图的面积应该相等,由取可估计中位数的值。3、平均数是直方图的“重心”(平衡点).三、2.02这个中位数的估计值,与样本的中位数值2.0不一样,你能解释其中的原因吗? 2、总体的各种数值特征都可以由两种途径来估计。
直接利用样本数据或由频率分布直方图来估计。
两种方法各有利弊;比如:1、通过频率分布直方图的估计精度低;2、通过频率分布直方图的估计结果与数据分组有关;3、在不能得到样本数据,只能得到频率分布直方图的情况下,也可以估计总体特征,而且直方图比较直观便于形象地进行分析。4、三种数字特征的优缺点 :(1)众数体现了样本数据的最大集中点,但它显然对其他数据信息的忽视使得无法客观地反映总体特征。(2)中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值不敏感有时也会成为缺点.(3)由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。但平均数受数据中的极端值的影响较大,使平均数在估计总体时可靠性降低。探究:例:某工厂人员及工资构成如下表:(1)指出这个问题中的众数、中位数、平均数;(2)这个问题中,平均数能客观地反映该工厂的工资水平吗?四、阅读课本63页的思考,举例分析对极端值不敏感的利与弊。五、练习 应该采用平均数来表示每一个国家项目的平均金额,因为它能反映所有项目的信息。但平均数会受到极端数据2200万元的影响,所以大多数项目投资金额都和平均数相差比较大。
2、中位数 将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数。练习: 某教师出了一份共3道题的测试卷,每题1分,全班得3分、2分、1分和0分的学生所占比例分别为:30%、50%、10%和10%。(1)若全班共有10人, 则平均分是多少?(2)若全班共有20人, 则平均分是多少?(3)若该班人数未知,能求出该班的平均分吗?5.画频率分布直方图复习回顾:画频率分布直方图步骤2.决定组距与组数(样本容量不超过100时,组数常分成5~12组)。 3.将数据分组(9组):
[0, 0.5) , [0.5, 1) ,~~,[4, 4.5)4.列频率分布表1.求极差(一组数据中最大值与最小值的 差)4.3-0.2=4 .1 ( t )。练习.(广东卷11)为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为,,分布直方图如图3,则这20名工人中一天生产的人数是 .该产品数量在由此得到频率二、思考:如何从频率分布直方图中估计众数?众数:2.25注:小长方形的面积=组距×频率/组距=频率
各长方形的面积总和等于1。复习:立方图中每个小长方形的面积表示什么意思?怎样从立方图中找到中位数?左边的数据个数等于右边数据的个数即左边的样本频数等于右边的样本频数个数即左边的样本频率等于右边的样本频率即立方图左、右边的小矩形的面积相等二、思考:如何从频率分布直方图中估计中位数?即中位数左边立方图的小矩形面积为0.5二、思考:如何从频率分布直方图中估计中位数?中位数左边立方图的小矩形面积为0.50~2的小矩形面积之和为:0.5×(0.8+0.16+0.30+0.44)=0.490.440.5-0.49=0.010.01/0.5=0.02如图在直线t=2.02之前所有小矩形的面积为0.5所以该样本的中位数为2.02练习.(广东11变式题1)为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为,,分布直方图如图3,则这20名工人中一天生产的中位数 .该产品数量在由此得到频率二、思考:如何从频率分布直方图中估计平均数?0.440.280.120.080.04练习.(广东11变式题2)为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为,,分布直方图如图3,则这20名工人中一天生产的平均数 .该产品数量在由此得到频率小结众数、中位数、平均数与频率分布直方图的关系:1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。2、中位数左边和右边的直方图的面积应该相等,由取可估计中位数的值。3、平均数是直方图的“重心”(平衡点).三、2.02这个中位数的估计值,与样本的中位数值2.0不一样,你能解释其中的原因吗? 2、总体的各种数值特征都可以由两种途径来估计。
直接利用样本数据或由频率分布直方图来估计。
两种方法各有利弊;比如:1、通过频率分布直方图的估计精度低;2、通过频率分布直方图的估计结果与数据分组有关;3、在不能得到样本数据,只能得到频率分布直方图的情况下,也可以估计总体特征,而且直方图比较直观便于形象地进行分析。4、三种数字特征的优缺点 :(1)众数体现了样本数据的最大集中点,但它显然对其他数据信息的忽视使得无法客观地反映总体特征。(2)中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值不敏感有时也会成为缺点.(3)由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。但平均数受数据中的极端值的影响较大,使平均数在估计总体时可靠性降低。探究:例:某工厂人员及工资构成如下表:(1)指出这个问题中的众数、中位数、平均数;(2)这个问题中,平均数能客观地反映该工厂的工资水平吗?四、阅读课本63页的思考,举例分析对极端值不敏感的利与弊。五、练习 应该采用平均数来表示每一个国家项目的平均金额,因为它能反映所有项目的信息。但平均数会受到极端数据2200万元的影响,所以大多数项目投资金额都和平均数相差比较大。
