【2024春人教版八下数学高效实用课件】17.1.2勾股定理的应用1 课件(共24张PPT)
文档属性
| 名称 | 【2024春人教版八下数学高效实用课件】17.1.2勾股定理的应用1 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
人教八下数学
同步优质课件
人教版八年级下册
17.1.2 勾股定理
的应用1
第十七章 勾股定理
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 会运用勾股定理解决简单的实际问题.
2.经历勾股定理的应用过程,熟练掌握其应用方法,明确应用条件.
学习目标
重点
难点
数学来源于生活,勾股定理的应用在生活中无处不在,观看下面视频,你们能理解曾小贤和胡一菲的做法吗?
新课引入
例1 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过 为什么
2m
1m
A
B
D
C
分析:可以看出,木板横着或竖着都不能从门框内通过,只能试试斜着能否通过.门框对角线AC的长度是斜着能通过的最大长度.求出AC,再与木板的宽比较,就能知道木板能否通过.
新知学习
一 利用勾股定理解决实际问题
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5
因为AC大于木板的宽2.2m,所以木板能从门框内通过.
2m
1m
A
B
D
C
A
B
D
C
O
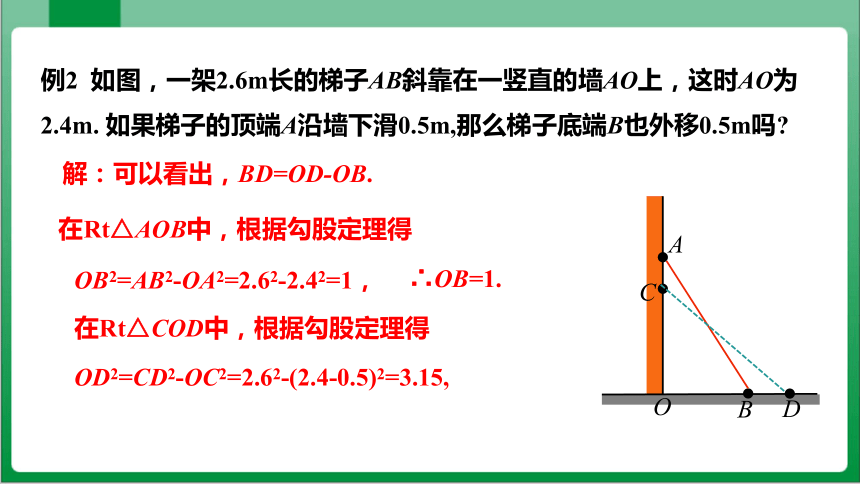
在Rt△AOB中,根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1,
∴OB=1.
在Rt△COD中,根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
例2 如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
解:可以看出,BD=OD-OB.
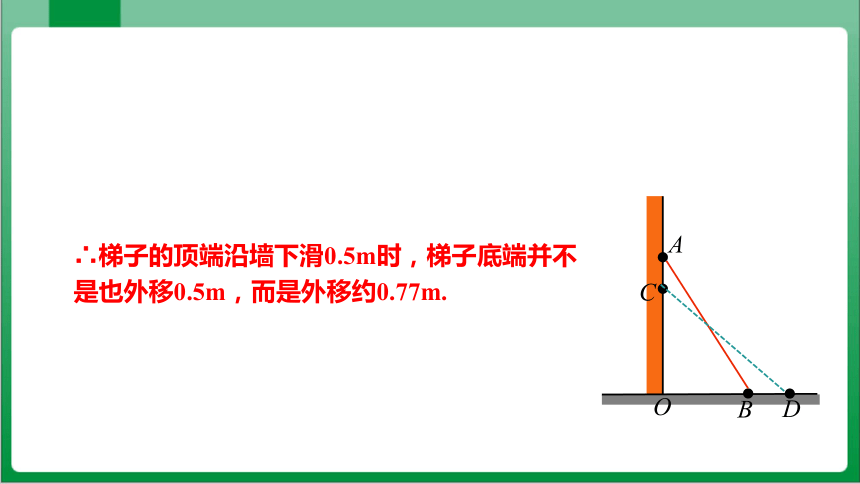
∴梯子的顶端沿墙下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
A
B
D
C
O
归纳
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
二 利用勾股定理解决点的距离及数学证明问题
例3 如图,在平面直角坐标系中有两点A(-3,5),B(1,2).求A,B两点间的距离.
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
y
O
x
3
B
C
解:如图,过点A作x轴的垂线交x轴于点D,过点B作x轴的垂线交x轴于点E,过点B作BC⊥AD.连接AB.
D
E
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
y
O
x
3
B
C
AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴A,B两点间的距离为5.
两点之间的距离公式:一般地,设平面上任意两点
思考
在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC 和Rt△A ′ B ′ C ′ 中,∠C=∠C ′=90°,AB=A′ B ′,AC=A′ C′ .
求证:△ABC≌△A ′B ′C′ .
A
B
C
A
B
C′
′
′
证明:在Rt△ABC 和Rt△A ′B ′C ′中,
∠C=∠C′=90°,
根据勾股定理得
A
B
C
A
B
C′
′
′
1.湖的两端有A、B两点,点C是与BA方向成直角的BC方向上一点,测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
随堂练习
2.如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
A.9cm B.12cm C.15cm D.18cm
D
3. 到了游乐园,小洛和小宇一起玩遥控赛车游戏,如图,终点为点A,小洛的赛车从点B出发,以3 dm/s的速度由南向北行驶,同时小宇的赛车从点C出发,以4 dm/s的速度由西向东行驶.已知AC = 4 m,AB = 3 m.出发3 s时,两赛车相距____dm.
第3题图
35
本题选自2024《情境题与中考新考法·讲评教案》
4. 如图,有两棵树,一棵高8米,另一棵高2米,两棵树相距8米. 一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少米?
A
B
C
解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.
5. 如图,一座城墙高 11.7 m,墙外有一条宽为 9 m 的护城河,那么一架长为 15 m 的云梯能否到达墙的顶端?
分析:要判断云梯能否到达城墙的顶端,只需求构建的直角三角形的斜边长和云梯的长比较大小.
解:设由城墙和护城河构成的直角三角形的斜边长为 x 米.
根据勾股定理得
x2 = 92 + 11.72=81 + 136.89 = 217.89 < 152,
所以云梯可以到达城墙的顶端.
用勾股定理解决实际问题
勾股定理
的应用
用勾股定理解决点的距离及数学证明问题
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
17.1.2 勾股定理
的应用1
第十七章 勾股定理
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 会运用勾股定理解决简单的实际问题.
2.经历勾股定理的应用过程,熟练掌握其应用方法,明确应用条件.
学习目标
重点
难点
数学来源于生活,勾股定理的应用在生活中无处不在,观看下面视频,你们能理解曾小贤和胡一菲的做法吗?
新课引入
例1 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过 为什么
2m
1m
A
B
D
C
分析:可以看出,木板横着或竖着都不能从门框内通过,只能试试斜着能否通过.门框对角线AC的长度是斜着能通过的最大长度.求出AC,再与木板的宽比较,就能知道木板能否通过.
新知学习
一 利用勾股定理解决实际问题
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5
因为AC大于木板的宽2.2m,所以木板能从门框内通过.
2m
1m
A
B
D
C
A
B
D
C
O
在Rt△AOB中,根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1,
∴OB=1.
在Rt△COD中,根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
例2 如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
解:可以看出,BD=OD-OB.
∴梯子的顶端沿墙下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
A
B
D
C
O
归纳
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
二 利用勾股定理解决点的距离及数学证明问题
例3 如图,在平面直角坐标系中有两点A(-3,5),B(1,2).求A,B两点间的距离.
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
y
O
x
3
B
C
解:如图,过点A作x轴的垂线交x轴于点D,过点B作x轴的垂线交x轴于点E,过点B作BC⊥AD.连接AB.
D
E
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
y
O
x
3
B
C
AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴A,B两点间的距离为5.
两点之间的距离公式:一般地,设平面上任意两点
思考
在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC 和Rt△A ′ B ′ C ′ 中,∠C=∠C ′=90°,AB=A′ B ′,AC=A′ C′ .
求证:△ABC≌△A ′B ′C′ .
A
B
C
A
B
C′
′
′
证明:在Rt△ABC 和Rt△A ′B ′C ′中,
∠C=∠C′=90°,
根据勾股定理得
A
B
C
A
B
C′
′
′
1.湖的两端有A、B两点,点C是与BA方向成直角的BC方向上一点,测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
随堂练习
2.如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
A.9cm B.12cm C.15cm D.18cm
D
3. 到了游乐园,小洛和小宇一起玩遥控赛车游戏,如图,终点为点A,小洛的赛车从点B出发,以3 dm/s的速度由南向北行驶,同时小宇的赛车从点C出发,以4 dm/s的速度由西向东行驶.已知AC = 4 m,AB = 3 m.出发3 s时,两赛车相距____dm.
第3题图
35
本题选自2024《情境题与中考新考法·讲评教案》
4. 如图,有两棵树,一棵高8米,另一棵高2米,两棵树相距8米. 一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少米?
A
B
C
解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.
5. 如图,一座城墙高 11.7 m,墙外有一条宽为 9 m 的护城河,那么一架长为 15 m 的云梯能否到达墙的顶端?
分析:要判断云梯能否到达城墙的顶端,只需求构建的直角三角形的斜边长和云梯的长比较大小.
解:设由城墙和护城河构成的直角三角形的斜边长为 x 米.
根据勾股定理得
x2 = 92 + 11.72=81 + 136.89 = 217.89 < 152,
所以云梯可以到达城墙的顶端.
用勾股定理解决实际问题
勾股定理
的应用
用勾股定理解决点的距离及数学证明问题
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
