甘肃省武威第二十六中学2023-2024学年第二学期九年级数学开学测试卷(含答案)
文档属性
| 名称 | 甘肃省武威第二十六中学2023-2024学年第二学期九年级数学开学测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 292.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 11:48:45 | ||
图片预览



文档简介
2023-2024学年第二学期甘肃省武威第二十六中学九年级数学开学测试卷
一、选择题(共30分)
1.(3分)下列方程是一元二次方程的是( )
A.x2﹣5x=3 B.x2﹣+1=0 C.3x2+y=2 D.x﹣3y+1=0
2.(3分)一元二次方程x2-8x-1=0配方后可变形为( )
A.(x+4)2=17 B.(x+4)2=15
C.(x-4)2=17 D.(x-4)2=15
3.(3分)若关于x的方程 有实数根,则实数k的取值范围是 ( )
A. B. 且
C. D.
4.(3分)等腰三角形的底和腰是方程的两个根,则这个三角形的周长为( )
A.7 B.8 C.7或8 D.不能确定
5.(3分)设a,b是方程的两个实数根,则的值为( )
A.2020 B.2021 C.2022 D.2023
6.(3分)对于抛物线,下列说法错误的是( )
A.开口向上 B.对称轴是直线
C.时,随的增大而减小 D.,函数有最小值
7.(3分)二次函数的开口方向、对称轴和顶点坐标分别为( )
A.向下、直线、 B.向下、直线、
C.向下、直线、 D.向上、直线、
8.(3分)如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得,若点在AB上,则的长为( )
A. B.4 C. D.5
9.(3分)如图,在△ABC中,∠A=30°,∠C=45°,BC=2,则的长度为( )
A. B. C.π D.2π
10.(3分) 七年级一班同学组织了元旦联欢会,文艺委员准备在“横扫千军”“飞花令”“成语接龙”“看图猜诗词”四个项目中选择两个,则她选中“飞花令”和“看图猜诗词”的概率为( )
A. B. C. D.
二、填空题(共24分)
11.(3分)关于x的一元二次方程的一个根是-1,则 .
12.(3分)已知实数,满足,,则 .
13.(3分)以原点为中心,把点逆时针旋转,得到点,点的坐标为 .
14.(3分)将抛物线向右平移一个单位,所得函数解析式为
15.(3分)在一个不透明口袋中装有1个红球和个白球,它们除了颜色以外没有任何其他区别.搅匀后从口袋中随机摸出1个球,记录下颜色后放回口袋中并搅匀,随着试验次数的增加,摸到白球的频率逐渐稳定在,则的值为 .
16.(3分)如图,在中,于点的长为,则弦的长为 .
17.(3分)如图,,是的切线,,是切点,若,则 .
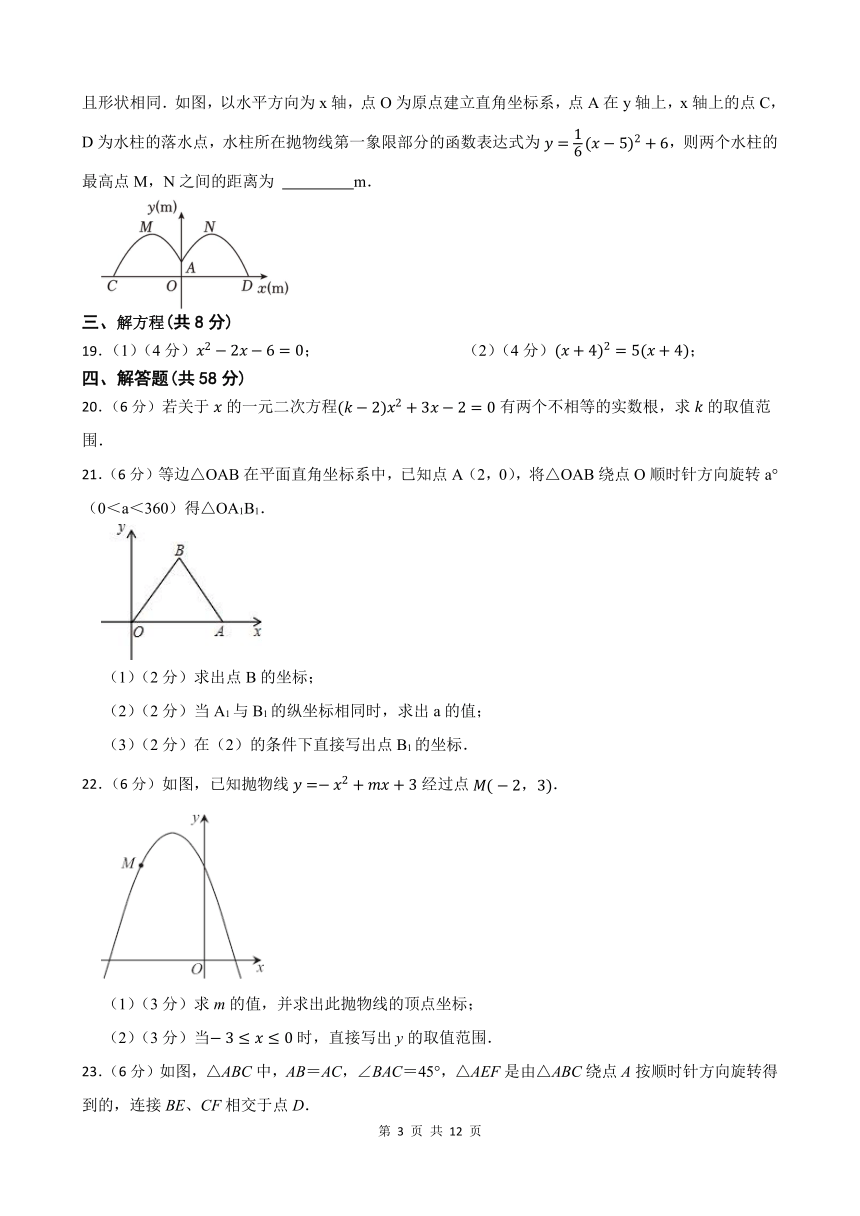
18.(3分)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为,则两个水柱的最高点M,N之间的距离为 m.
三、解方程(共8分)
19.(1)(4分); (2)(4分);
四、解答题(共58分)
20.(6分)若关于的一元二次方程有两个不相等的实数根,求的取值范围.
21.(6分)等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.
(1)(2分)求出点B的坐标;
(2)(2分)当A1与B1的纵坐标相同时,求出a的值;
(3)(2分)在(2)的条件下直接写出点B1的坐标.
22.(6分)如图,已知抛物线经过点.
(1)(3分)求m的值,并求出此抛物线的顶点坐标;
(2)(3分)当时,直接写出y的取值范围.
23.(6分)如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
(1)(3分)求证:BE=CF;
(2)(3分)求∠BDC的度数.
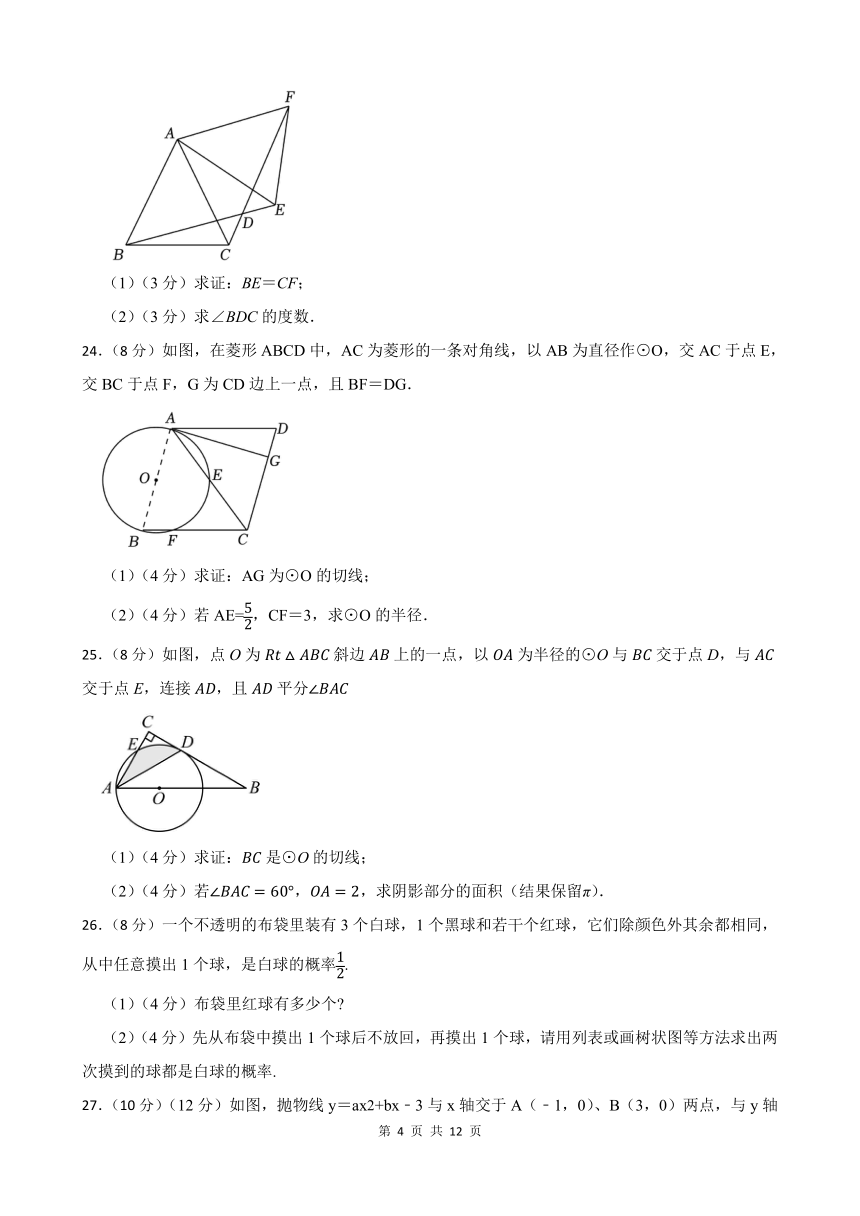
24.(8分)如图,在菱形ABCD中,AC为菱形的一条对角线,以AB为直径作⊙O,交AC于点E,交BC于点F,G为CD边上一点,且BF=DG.
(1)(4分)求证:AG为⊙O的切线;
(2)(4分)若AE=,CF=3,求⊙O的半径.
25.(8分)如图,点O为斜边上的一点,以为半径的⊙O与交于点D,与交于点E,连接,且平分
(1)(4分)求证:是⊙O的切线;
(2)(4分)若,,求阴影部分的面积(结果保留π).
26.(8分)一个不透明的布袋里装有3个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率.
(1)(4分)布袋里红球有多少个
(2)(4分)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率.
27.(10分)(12分)如图,抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C.
(1)(3分)求抛物线的解析式;
(2)(3分)若点D是抛物线上的一点,当△ABD的面积为10时,求点D的坐标;
(3)(4分)点P是抛物线对称轴上的一点,在抛物线上是否存在一点Q,使得以B、C、P、Q为顶点的四边形是平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由.
答案
1-10 ACDCC CBACB
11.0 12.或2 13.(1,2) 14. 15.4 16. 17. 18.10
19.(1)解:x2-2x-6=0,
x2-2x=6 ,
x2-2x+1=6+1 ,
(x-1)2=7 ,
x-1=,
∴x1=,x2=
(2)解:,
,
,
或,
,
20.解:由题意知:,
方程有两个不相等的实数根,
且,
即,
解得,
且.
21.(1)解:如图1所示过点B作BC⊥OA,垂足为C.
∵△OAB为等边三角形,
∴∠BOC=60°,OB=BA.
∵OB=AB,BC⊥OA,
∴OC=CA=1.
在Rt△OBC中, ,
∴BC= .
∴点B的坐标为(1, )
(2)解:如图2所示:
∵点B1与点A1的纵坐标相同,
∴A1B1∥OA.
如图2所示:当a=300°时,点A1与点B1纵坐标相同.
如图3所示:当a=120°时,点A1与点B1纵坐标相同.
∴当a=120°或a=300°时,点A1与点B1纵坐标相同
(3)解:如图2所示:由旋转的性质可知A1B1=AB=2,点B的坐标为(1,2),
∴点B1的坐标为(﹣1, ).
如图3所示:由旋转的性质可知:点B1的坐标为(1,﹣ ).
∴点B1的坐标为(﹣1, )或(1,﹣ )
22.(1)解:将代入,得:
解得:
此抛物线的顶点坐标为.
(2)解:由(1)可知抛物线的顶点坐标为,对称轴为直线,
当时,,
当时,y的取值范围为:.
23.(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC,
∴AE=AF,
∴△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴BE=CF;
(2)解:∵△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴△AEB≌△AFC,
∴∠ABE=∠ACF,
设AC与BE相交于O,
∵∠AOB=∠COD,
∴∠BDC=∠BAC=45°.
24.(1)证明:如图:连接AF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,AB∥DC,
在△ABF和△ADG中,
,
∴△ABF≌△ADG(SAS),
∴∠AFB=∠AGD=90°,
∵AB∥DC,
∴∠BAG=∠AGD=90°,
∴OA⊥AG,
又∵OA是⊙O的半径,
∴AG为⊙O的切线;
(2)解:如图:连接BE,
∵AB是⊙O的直径,
∴∠AEB=90°,即BE⊥AC,
∵四边形ABCD是菱形,
∴AB=BC,
∴AC=2AE=2=5,
设⊙O的半径为R,则AB=BC=2R,则BF=BC﹣CF=2R﹣3,
∵AF2=AB2﹣BF2=AC2﹣CF2,
∴(2R)2﹣(2R﹣3)2=52﹣32,
解得R=,
故⊙O的半径为.
25.(1)证明:连接,如图
∵平分,
∴,
∵,
∴,
∴,
∴,
∵,即
∴,
∵是⊙O的半径,
∴是⊙O的切线;
(2)解:如图,连接,,交于点M,
∵,,
∴为等边三角形,
∴,,
∴,
又由(1)知,,即,
∴四边形为平行四边形,
∵,
∴四边形是菱形,
,
∴,
∴
26.(1)解:设红球的个数为x,由题意可得:,解得:,经检验是方程的根.
答:布袋里的红球有2个;
(2)解:画树状图如下:
由树状图可知共有30种均等可能结果,两次摸到的球都是白球的有6种可能
(摸得两白).
27.(1)将A(﹣1,0)、B(3,0)代入y=ax2+bx﹣3得,
,
解得:,
∴抛物线的解析式为:y=x2﹣2x﹣3;
(2)设点D的坐标为(x,x2﹣2x﹣3),
∵A(﹣1,0)、B(3,0),
∴AB=4,
∴,
即|x2﹣2x﹣3|=5,
∴x2﹣2x﹣3=5或x2﹣2x﹣3=﹣5(无解舍去),
解得:x1=4,x2=﹣2,
∴点D的坐标为(4,5)或(﹣2,5);
(3)在抛物线上存在一点Q,使得以B、C、P、Q为顶点的四边形是平行四边形;理由如下:
抛物线y=x2﹣2x﹣3的对称轴为:x=1,
假设存在,设P(xp,yP),Q(xQ,yQ),
∴xp=1,
分两种情况讨论:
当BC为四边形的对角线时,PB∥CQ,PB=CQ,
∴|xB﹣xP|=|xQ﹣xC|,
即2=xQ,
此时点Q的坐标为(2,﹣3);
②当BC为边时,PQ∥BC,PQ=CB,
∴|xQ﹣xP|=|xB﹣xC|,即|xQ﹣1|=3,
解得:xQ=4或xQ=﹣2,
此时点Q的坐标为(4,5)或(﹣2,5).
综上所述,存在满足条件的Q点的坐标为(2,﹣3)或(4,5)或(﹣2,5).
一、选择题(共30分)
1.(3分)下列方程是一元二次方程的是( )
A.x2﹣5x=3 B.x2﹣+1=0 C.3x2+y=2 D.x﹣3y+1=0
2.(3分)一元二次方程x2-8x-1=0配方后可变形为( )
A.(x+4)2=17 B.(x+4)2=15
C.(x-4)2=17 D.(x-4)2=15
3.(3分)若关于x的方程 有实数根,则实数k的取值范围是 ( )
A. B. 且
C. D.
4.(3分)等腰三角形的底和腰是方程的两个根,则这个三角形的周长为( )
A.7 B.8 C.7或8 D.不能确定
5.(3分)设a,b是方程的两个实数根,则的值为( )
A.2020 B.2021 C.2022 D.2023
6.(3分)对于抛物线,下列说法错误的是( )
A.开口向上 B.对称轴是直线
C.时,随的增大而减小 D.,函数有最小值
7.(3分)二次函数的开口方向、对称轴和顶点坐标分别为( )
A.向下、直线、 B.向下、直线、
C.向下、直线、 D.向上、直线、
8.(3分)如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得,若点在AB上,则的长为( )
A. B.4 C. D.5
9.(3分)如图,在△ABC中,∠A=30°,∠C=45°,BC=2,则的长度为( )
A. B. C.π D.2π
10.(3分) 七年级一班同学组织了元旦联欢会,文艺委员准备在“横扫千军”“飞花令”“成语接龙”“看图猜诗词”四个项目中选择两个,则她选中“飞花令”和“看图猜诗词”的概率为( )
A. B. C. D.
二、填空题(共24分)
11.(3分)关于x的一元二次方程的一个根是-1,则 .
12.(3分)已知实数,满足,,则 .
13.(3分)以原点为中心,把点逆时针旋转,得到点,点的坐标为 .
14.(3分)将抛物线向右平移一个单位,所得函数解析式为
15.(3分)在一个不透明口袋中装有1个红球和个白球,它们除了颜色以外没有任何其他区别.搅匀后从口袋中随机摸出1个球,记录下颜色后放回口袋中并搅匀,随着试验次数的增加,摸到白球的频率逐渐稳定在,则的值为 .
16.(3分)如图,在中,于点的长为,则弦的长为 .
17.(3分)如图,,是的切线,,是切点,若,则 .
18.(3分)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为,则两个水柱的最高点M,N之间的距离为 m.
三、解方程(共8分)
19.(1)(4分); (2)(4分);
四、解答题(共58分)
20.(6分)若关于的一元二次方程有两个不相等的实数根,求的取值范围.
21.(6分)等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.
(1)(2分)求出点B的坐标;
(2)(2分)当A1与B1的纵坐标相同时,求出a的值;
(3)(2分)在(2)的条件下直接写出点B1的坐标.
22.(6分)如图,已知抛物线经过点.
(1)(3分)求m的值,并求出此抛物线的顶点坐标;
(2)(3分)当时,直接写出y的取值范围.
23.(6分)如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
(1)(3分)求证:BE=CF;
(2)(3分)求∠BDC的度数.
24.(8分)如图,在菱形ABCD中,AC为菱形的一条对角线,以AB为直径作⊙O,交AC于点E,交BC于点F,G为CD边上一点,且BF=DG.
(1)(4分)求证:AG为⊙O的切线;
(2)(4分)若AE=,CF=3,求⊙O的半径.
25.(8分)如图,点O为斜边上的一点,以为半径的⊙O与交于点D,与交于点E,连接,且平分
(1)(4分)求证:是⊙O的切线;
(2)(4分)若,,求阴影部分的面积(结果保留π).
26.(8分)一个不透明的布袋里装有3个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率.
(1)(4分)布袋里红球有多少个
(2)(4分)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率.
27.(10分)(12分)如图,抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C.
(1)(3分)求抛物线的解析式;
(2)(3分)若点D是抛物线上的一点,当△ABD的面积为10时,求点D的坐标;
(3)(4分)点P是抛物线对称轴上的一点,在抛物线上是否存在一点Q,使得以B、C、P、Q为顶点的四边形是平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由.
答案
1-10 ACDCC CBACB
11.0 12.或2 13.(1,2) 14. 15.4 16. 17. 18.10
19.(1)解:x2-2x-6=0,
x2-2x=6 ,
x2-2x+1=6+1 ,
(x-1)2=7 ,
x-1=,
∴x1=,x2=
(2)解:,
,
,
或,
,
20.解:由题意知:,
方程有两个不相等的实数根,
且,
即,
解得,
且.
21.(1)解:如图1所示过点B作BC⊥OA,垂足为C.
∵△OAB为等边三角形,
∴∠BOC=60°,OB=BA.
∵OB=AB,BC⊥OA,
∴OC=CA=1.
在Rt△OBC中, ,
∴BC= .
∴点B的坐标为(1, )
(2)解:如图2所示:
∵点B1与点A1的纵坐标相同,
∴A1B1∥OA.
如图2所示:当a=300°时,点A1与点B1纵坐标相同.
如图3所示:当a=120°时,点A1与点B1纵坐标相同.
∴当a=120°或a=300°时,点A1与点B1纵坐标相同
(3)解:如图2所示:由旋转的性质可知A1B1=AB=2,点B的坐标为(1,2),
∴点B1的坐标为(﹣1, ).
如图3所示:由旋转的性质可知:点B1的坐标为(1,﹣ ).
∴点B1的坐标为(﹣1, )或(1,﹣ )
22.(1)解:将代入,得:
解得:
此抛物线的顶点坐标为.
(2)解:由(1)可知抛物线的顶点坐标为,对称轴为直线,
当时,,
当时,y的取值范围为:.
23.(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC,
∴AE=AF,
∴△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴BE=CF;
(2)解:∵△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴△AEB≌△AFC,
∴∠ABE=∠ACF,
设AC与BE相交于O,
∵∠AOB=∠COD,
∴∠BDC=∠BAC=45°.
24.(1)证明:如图:连接AF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,AB∥DC,
在△ABF和△ADG中,
,
∴△ABF≌△ADG(SAS),
∴∠AFB=∠AGD=90°,
∵AB∥DC,
∴∠BAG=∠AGD=90°,
∴OA⊥AG,
又∵OA是⊙O的半径,
∴AG为⊙O的切线;
(2)解:如图:连接BE,
∵AB是⊙O的直径,
∴∠AEB=90°,即BE⊥AC,
∵四边形ABCD是菱形,
∴AB=BC,
∴AC=2AE=2=5,
设⊙O的半径为R,则AB=BC=2R,则BF=BC﹣CF=2R﹣3,
∵AF2=AB2﹣BF2=AC2﹣CF2,
∴(2R)2﹣(2R﹣3)2=52﹣32,
解得R=,
故⊙O的半径为.
25.(1)证明:连接,如图
∵平分,
∴,
∵,
∴,
∴,
∴,
∵,即
∴,
∵是⊙O的半径,
∴是⊙O的切线;
(2)解:如图,连接,,交于点M,
∵,,
∴为等边三角形,
∴,,
∴,
又由(1)知,,即,
∴四边形为平行四边形,
∵,
∴四边形是菱形,
,
∴,
∴
26.(1)解:设红球的个数为x,由题意可得:,解得:,经检验是方程的根.
答:布袋里的红球有2个;
(2)解:画树状图如下:
由树状图可知共有30种均等可能结果,两次摸到的球都是白球的有6种可能
(摸得两白).
27.(1)将A(﹣1,0)、B(3,0)代入y=ax2+bx﹣3得,
,
解得:,
∴抛物线的解析式为:y=x2﹣2x﹣3;
(2)设点D的坐标为(x,x2﹣2x﹣3),
∵A(﹣1,0)、B(3,0),
∴AB=4,
∴,
即|x2﹣2x﹣3|=5,
∴x2﹣2x﹣3=5或x2﹣2x﹣3=﹣5(无解舍去),
解得:x1=4,x2=﹣2,
∴点D的坐标为(4,5)或(﹣2,5);
(3)在抛物线上存在一点Q,使得以B、C、P、Q为顶点的四边形是平行四边形;理由如下:
抛物线y=x2﹣2x﹣3的对称轴为:x=1,
假设存在,设P(xp,yP),Q(xQ,yQ),
∴xp=1,
分两种情况讨论:
当BC为四边形的对角线时,PB∥CQ,PB=CQ,
∴|xB﹣xP|=|xQ﹣xC|,
即2=xQ,
此时点Q的坐标为(2,﹣3);
②当BC为边时,PQ∥BC,PQ=CB,
∴|xQ﹣xP|=|xB﹣xC|,即|xQ﹣1|=3,
解得:xQ=4或xQ=﹣2,
此时点Q的坐标为(4,5)或(﹣2,5).
综上所述,存在满足条件的Q点的坐标为(2,﹣3)或(4,5)或(﹣2,5).
同课章节目录
