新人教版数学九年级下册第二十八章锐角三角函数28.2《解直角三角形及应用》课时练习.doc
文档属性
| 名称 | 新人教版数学九年级下册第二十八章锐角三角函数28.2《解直角三角形及应用》课时练习.doc |

|
|
| 格式 | doc | ||
| 文件大小 | 640.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-20 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
新人教版数学九年级下册第28章28.2解直角三角形及其应用
课时作业
一、选择题
1. 如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC= ,则边BC的长为( )
A.30cm B.20cm C.10cm D.5cm
答案:C
知识点:解直角三角形
解析:解答:在直角三角形ABC中,根据三角函数定义可知:
tan∠BAC= ,又AC=30cm,tan∠BAC=,
则BC=ACtan∠BAC=30×=10cm.
故选C.
分析:此题考查学生掌握三角函数正弦、余弦及正切的定义,是一道基础题.要求注意观察生活中的数学问题,培养学生利用数学知识解决实际问题的能力,体现了数学来自于生活且服务于生活.
因为教学用的直角三角板为直角三角形,所以利用三角函数定义,一个角的正切值等于这个角的对边比邻边可知∠BAC的对边为BC,邻边为AC,根据∠BAC的正切值,即可求出BC的长度.
2. 在“测量旗杆的高度”的数学课题学习中,某学习小组测得太阳光线与水平面的夹角为27°,此时旗杆在水平地面上的影子的长度为24米,则旗杆的高度约为( )
A.24米 B. 20米 C. 16米 D. 12米
答案:D
知识点:解直角三角形的应用
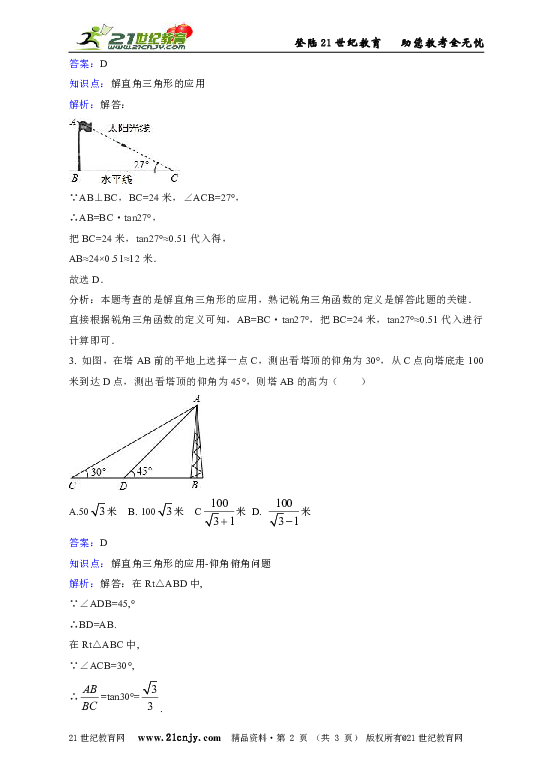
解析:解答:
∵AB⊥BC,BC=24米,∠ACB=27°,
∴AB=BC·tan27°,
把BC=24米,tan27°≈0.51代入得,
AB≈24×0.51≈12米.
故选D.
分析:本题考查的是解直角三角形的应用,熟记锐角三角函数的定义是解答此题的关键.
直接根据锐角三角函数的定义可知,AB=BC·tan27°,把BC=24米,tan27°≈0.51代入进行计算即可.
3. 如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为( )
A.50米 B. 100米 C米 D. 米
答案:D
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:在Rt△ABD中,
∵∠ADB=45,°
∴BD=AB.
在Rt△ABC中,
∵∠ACB=30°,
∴=tan30°=.
∴BC=AB.
设AB=x(米),
∵CD=100,
∴BC=x+100.
∴x+100=x,
∴x=米.
故选D.
分析:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
首先根据题意分析图形;本题涉及到两个直角三角形,设AB=x(米),再利用CD=BC-BD=100的关系,进而可解即可求出答案.
4. 某水坝的坡度i=1:,坡长AB=20米,则坝的高度为( )
A.10米 B.20米 C.40米 D.20
答案:A.
知识点:解直角三角形的应用-坡度坡角问题
解析:解答:如图:
∵坡度i=1: ,
∴设AC=x,BC=x.
根据勾股定理得
AC2+BC2=AB2,
则x2+(x)2=202,
解得x=10.
故选A.
分析:此题考查了坡比的概念,不仅要熟悉解直角三角形的知识,还要熟悉勾股定理.
画出图形,根据坡度的定义__-直角三角形中,坡角的正切值,然后利用解直角三角形的知识解答.
5. 如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10米 B.10米 C.20米 D. 米
答案:A
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:∵在直角三角形ADB中,∠D=30°,
∴=tan30°,
∴BD==AB .
∴在直角三角形ABC中,∠ACB=60°.
∴BC==AB.
∵CD=20,
∴CD=BD-BC=AB-AB=20.
解得:AB=10.
故选A.
分析:本题考查仰角的定义,要求学生能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形.
首先根据题意分析图形;本题涉及到两个直角三角形,应利用其公共边AB及CD=DC-BC=20构造方程关系式,进而可解,即可求出答案.
6. 如图,某水库堤坝横断面迎水坡AB的坡比是1:,堤坝高BC=50m,则迎水坡面AB的长度是( )
A.100m B.100m C.150mD.50 m
答案:A
知识点:解直角三角形的应用-坡度坡角问题
解析:解答:∵堤坝横断面迎水坡AB的坡比是1:,
∴=.
∵BC=50m,
∴AC=50m.
∴AB==100m.
故选:A.
分析:此题主要考查了解直角三角形的应用-坡度问题,关键是掌握坡度是坡面的铅直高度h和水平宽度l的比.
根据题意可得=,把BC=50m,代入即可算出AC的长,再利用勾股定理算出AB的长即可.
7. 如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.100(+1)米
答案:D
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:由已知,得∠A=30°,∠B=45°,CD=100,
∵CD⊥AB于点D,
∴在Rt△ACD中,∠CDA=90°,tanA=.
∴AD===100.
在Rt△BCD中,∠CDB=90°,∠B=45°,
∴DB=CD=100米.
∴AB=AD+DB=100+100=100(+1)米.
故选D.
分析:本题考查了解直角三角形的应用,解决本题的关键是利用CD为直角△ABC斜边上的高,将三角形分成两个三角形,然后求解.分别在两三角形中求出AD与BD的长.
图中两个直角三角形中,都是知道已知角和对边,根据正切函数求出邻边后,相加求和即可.
8. 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有( )
A.1组 B.2组 C.3组 D.4组
答案:C
知识点:解直角三角形的应用
解析:解答:此题比较综合,要多方面考虑,
①因为知道∠ACB和BC的长,所以可利用∠ACB的正切来求AB的长;
②可利用∠ACB和∠ADB的正切求出AB;
③,因为△ABD∽△EFD可利用,求出AB;
④无法求出A,B间距离.
故共有3组可以求出A,B间距离.
故选C.
分析:本题考查相似三角形的应用和解直角三角形的应用,解答道题的关键是将实际问题转化为数学问题,本题只要把实际问题抽象到相似三角形,解直角三角形即可求出.
根据三角形相似可知,要求出AB,只需求出EF即可.所以借助于相似三角形的性质,根据即可解答.
9. 如图,△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是( )
A. B. 12 C.14 D.21
答案:A
知识点:解直角三角形的应用
解析:解答:过点A作AD⊥BC,
∵△ABC中,cosB=,sinC=,AC=5,
∴cosB==.
∴∠B=45°.
∵sinC===,
∴AD=3.
∴CD==4.
∴BD=3.
则△ABC的面积是:×AD×BC=×3×(3+4)=.
故选A.
分析:此题主要考查了解直角三角形的知识,作出AD⊥BC,进而得出相关线段的长度是解决问题的关键.
根据已知作出三角形的高线AD,进而得出AD,BD,CD,的长,即可得出三角形的面积.
10. (2011 荆州)在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )
A. B. C. D.
答案:D
知识点:解直角三角形的应用
解析:解答:
延长BA作CD⊥BD,
∵∠A=120°,AB=4,AC=2,
∴∠DAC=60°,∠ACD=30°.
∴2AD=AC=2,
∴AD=1,CD=,
∴BD=5,
∴BC=2,
∴sinB==.
故选:D.
分析:此题主要考查了解直角三角形以及勾股定理的应用,根据题意得出∠DAC=60°,∠ACD=30°是解决问题的关键.
根据∠A=120°,得出∠DAC=60°,∠ACD=30°,得出AD=1,CD=,再根据BC=2,利用解直角三角形求出.
11. 如图所示,渔船在A处看到灯塔C在北偏东60°方向上,渔船正向东方向航行了12海里到达B处,在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离是( )
A.12海里 B.6海里 C. 6海里D. 4海里
答案:D
知识点:解直角三角形的应用-方向角问题
解析:解答:由已知得:∠BAC=90°-60°=30°,
在直角三角形ABC中,
BC=ABtan30°=12×=4(海里).
故选:D.
分析:此题考查的知识点是解直角三角形的应用,关键是先得∠BAC=30°,再解直角三角形ABC即可.
此题易得∠BAC=30°,再由直角三角形ABC运用三角函数求得渔船与灯塔C的距离BC.
12. 如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于( )
A. msin米 B.mtan米 C.mcos米 D. 米
答案:B
知识点:解直角三角形的应用
解析:解答:在直角△ABC中,tan=,
∴AB=mtan.
故选B.
分析:此题考查了三角函数的基本概念,主要是正切概念及运算.
在直角△ABC中,已知∠α及其邻边,求∠α的对边,根据三角函数定义即可求解.
13. 如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
A. (+)m B. (+)m C. m D.4m
答案:A
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:∵AD=BE=5米,∠CAD=30°,
∴CD=ADtan30°=5×=(米).
∴CE=CD+DE=CD+AB=+(米).
故选A.
分析:此题主要考查学生对坡度坡角的理解及解直角三角形的综合运用能力.
应先根据相应的三角函数值算出CD长,再加上AB长即为树高.
14. 一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( )
A. (30-50,30) B. (30, 30-50)C. (30,30) D.(30, 30)
答案:A
知识点:解直角三角形的应用-方向角问题
解析:解答:过点A作AC⊥x轴于C.
在直角△OAC中,∠AOC=30°,OA=4×15=60海里,则AC=OA=30海里,OC=30海里.
因而A所在位置的坐标是(30,30).
小岛B在A的正西50海里处,因而小岛B所在位置的坐标是(30-50,30).
故选A.
分析:本题主要考查了方向角含义,正确记忆三角函数的定义是解决本题的关键.
过点A作AC⊥x轴于C,根据已知可求得点A的坐标,从而根据已知求点B的坐标.
15. 在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A、C两地的距离为( )
A. km B. km C. km D. km
答案:A
知识点:解直角三角形的应用-方向角问题
解析:解答:如图.由题意可知,AB=5km,∠2=30°,∠EAB=60°,∠3=30°.
∵EF∥PQ,
∴∠1=∠EAB=60°
又∵∠2=30°,
∴∠ABC=180°-∠1-∠2=180°-60°-30°=90°.
∴△ABC是直角三角形.
又∵MN∥PQ,
∴∠4=∠2=30°.
∴∠ACB=∠4+∠3=30°+30°=60°.
∴AC===(km).
故选A.
分析:本题是方向角问题在实际生活中的运用,解答此类题目的关键是根据题意画出图形利用解直角三角形的相关知识解答.
根据已知作图,由已知可得到△ABC是直角三角形,从而根据三角函数即可求得AC的长.
二、选择题
1. 数学实践探究课中,老师布置同学们测量学校旗杆的高度.小民所在的学习小组在距离旗杆底部10米的地方,用测角仪测得旗杆顶端的仰角为60°,则旗杆的高度是____
答案:10米
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:如图,根据题意得:AC=10米,∠ACB=60°,
∵∠A=90°,
∴在Rt△ABC中,AB=ACtan∠ACB=10×tan60°=10×=10(米).故答案为:10.
分析:本题考查仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.
由根据题意得:AC=10米,∠ACB=60°,然后再在Rt△ABC中,利用正切函数,即可求得旗杆的高度.
2. 如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是____
答案:210cm.
知识点:解直角三角形的应用-坡度坡角问题
解析:解答:过点B作BD⊥AC于D,
根据题意得:AD=2×30=60(cm),BD=18×3=54(cm),
∵斜坡BC的坡度i=1:5,
∴BD:CD=1:5,
∴CD=5BD=5×54=270(cm),
∴AC=CD-AD=270-60=210(cm).
∴AC的长度是210cm.
故答案为:210.
分析:此题考查了解直角三角形的应用:坡度问题.此题难度适中,注意掌握坡度的定义,注意数形结合思想的应用与辅助线的作法.
首先过点B作BD⊥AC于D,根据题意即可求得AD与BD的长,然后由斜坡BC的坡度i=1:5,求得CD的长,继而求得答案.
3. 如图,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°.根据图形计算tan15°=____
答案:2-.
知识点:解直角三角形的应用
解析:解答:由已知设AB=AC=2x,
∵∠A=30°,CD⊥AB,
∴CD=AC=x,
则AD2=AC2-CD2=(2x)2-x2=3x2,
∴AD=x,
∴BD=AB-AD=2x-
x=(2-)x,
∴tan15°===2-.
故答案为:2-.
分析:此题考查的知识点是解直角三角形,关键是由直角三角形中30°角的性质与勾股定理先求出CD与AD,再求出BD.
此题可设AB=AC=x,由已知可求出CD和AD,那么也能求出BD=AB-AD,从而求出tan15°.
4. 如图,为测量旗杆AB的高度,在与B距离为8米的C处测得旗杆顶端A的仰角为56°,那么旗杆的高度约是____米(结果保留整数).(参考数据:sin56°≈0.829,cos56°≈0.559,tan56°≈1.483)
答案:12
知识点:解直角三角形的应用
解析:解答:由题意知BC=8,∠C=56°,
故AB=BCtan56°≈8×1.483≈12米,
故答案为12.
分析:本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形并选择合适的边角关系求解.在直角三角形ABC中,根据BC=8,∠ACB=56°即可求得AB的长.
5. 如图,为了测量电线杆AB的高度,小明将测量仪放在与电线杆的水平距离为9m的D处.若测角仪CD的高度为1.5m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为____(精确到0.1m).(参考数据sin36°≈0.59.cos36°≈0.81,tan36°≈0.73).
答案:8.1 m.
知识点:解直角三角形的应用
解析:解答:
如图,在Rt△ACE中,
∴AE=CEtan36°
=BDtan36°
=9×tan36°
≈6.57米,
∴AB=AE+EB=AE+CD=6.57+1.5≈8.1(米).
故答案为:8.1.
分析:本题考查了三角函数在直角三角形中的运用,本题中正确计算AE的值是解题的关键.
根据CE和tan36°可以求得AE的长度,根据AB=AE+EB即可求得AB的长度,即可解题.
三、解答题
1. 为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,≈1.73,精确到个位)
答案:隧道AB的长为245m.
知识点:解直角三角形
解析:解答:
过点C作CD⊥AB于D,
∵BC=200m,∠CBA=30°,
∴在Rt△BCD中,CD=
BC=100m,BD=BCcos30°=200×=100≈173(m),
∵∠CAB=54°,
在Rt△ACD中,AD=≈≈72(m),
∴AB=AD+BD=173+72=245(m).
答:隧道AB的长为245m.
分析:此题考查了解直角三角形的应用.此题难度适中,注意掌握辅助线的作法,注意把实际问题转化为数学问题求解.
首先过点C作CD⊥AB于D,然后在Rt△BCD中,利用三角函数的知识,求得BD,CD的长,继而在Rt△ACD中,利用∠CAB的正切求得AD的长,继而求得答案.
2. 如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.(取1.73,结果保留整数.)
答案:建筑物CD的高约为47 m.
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:
过点P作PE⊥CD于E,则四边形BCEP是矩形.
∴PE=BC=30.
在Rt△PDE中,∵∠DPE=30°,PE=30,
∴DE=PE×tan30°=30×=10.
在Rt△PEC中,∵∠EPC=45°,PE=30,
∴CE=PE×tan45°=30×1=30.
∴CD=DE﹢CE=30﹢10=30﹢17.3≈47(m)
答:建筑物CD的高约为47 m.
分析:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
过点P作PE⊥CD于E,则四边形BCEP是矩形,得到PE=BC=30,在Rt△PDE中,利用∠DPE=30°,PE=30,求得DE的长;在Rt△PEC中,利用∠EPC=45°,PE=30求得CE的长,利用CD=DE﹢CE即可求得结果.
3. 如图,在Rt△ABC中,∠ACB=90°,已知CD⊥AB,BC=1
(1)如果∠BCD=30°,求AC;
(2)如果tan∠BCD=,求CD.
答案:(1)AC=;(2)CD=
知识点:解直角三角形
解析:解答:(1)∵CD⊥AB,∴∠BDC=90°,
∵∠DCB=30°,∴∠B=60°,
在Rt△ACB中,∠ACB=90°,
∴tan60°==,又BC=1,
则AC=;
(2)在Rt△BDC中,tan∠BCD==,
设BD=k,则CD=3k,又BC=1,
利用勾股定理得:k2+(3k)2=1,
解得:k=或k=-(舍去),
则CD=3k=.
分析:此题属于解三角形的题型,涉及的知识有:勾股定理,锐角三角函数定义,比例的性质,以及特殊角的三角函数值,是一道多知识点的综合题.
(1)根据直角三角形的两锐角互余,由∠BCD的度数求出∠B的度数,利用锐角三角函数定义表示出tanB,将tanB及BC的长代入,即可求出AC的长;
(2)在直角三角形BDC中,由已知tan∠BCD的值,利用锐角三角函数定义得出BD与CD的比值为1:3,根据比值设出BD=k,CD=3k,再由BC的长,利用勾股定理列出关于k的方程,求出方程的解得到k的值,即可求出CD的长.
4. 如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据≈1.41,≈1.73)
答案:A、C之间的距离为10.3海里.
知识点:解直角三角形的应用-方向角问题
解析:解答:
作AD⊥BC,垂足为D,
由题意得,∠ACD=45°,∠ABD=30°,
设CD=x,在Rt△ACD中,可得AD=x,
在Rt△ABD中,可得BD=x,
又∵BC=20,即x+x=20,解得:x=10(-1)
∴AC=x≈10.3(海里).
答:A、C之间的距离为10.3海里.
分析:此题考查了解直角三角形的应用,解答本题的关键是根据题意构造直角三角形,将实际问题转化为数学模型进行求解,难度一般.
作AD⊥BC,垂足为D,设CD=x,利用解直角三角形的知识,可得出AD,继而可得出BD,结合题意BC=CD+BD=20海里可得出方程,解出x的值后即可得出答案.
5. 如图,拦水坝的横断面为梯形ABCD,坝顶宽AD=5米,斜坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
(1)求斜坡AB的长;
(2)求拦水坝的横断面梯形ABCD的周长.(注意:本题中的计算过程和结果均保留根号)
答案:(1)斜坡AB的长为6m;(2)拦水坝的横断面梯形ABCD的周长为(37+6
+3)m.
知识点:解直角三角形的应用-坡度坡角问题
解析:解答:
(1)∵=i=,AE=6,
∴BE=3AE=18,在Rt△ABE中,根据勾股定理得: AB=
=6,
答:斜坡AB的长为6m;
(2)过点D作DF⊥BC于F,
可得四边形AEFD是矩形,
故EF=AD,∵AD=5,∴EF=5,
∵=i=,
DF=AE=6,
∴CF=DF=9,
∴BC=BE+EF+CF=18+5+9=32,
在Rt△DCF中,根据勾股定理得:
DC=
=3,
∴梯形ABCD的周长为:AB+BC+CD+DA=6+32+3+5=37+6+3,
答:拦水坝的横断面梯形ABCD的周长为(37+6
+3)m.
分析:此题主要考查了坡度的定义以及勾股定理的应用,根据已知坡度定义得出BE,FC的长是解题关键.
(1)根据坡度的定义得出BE的长,进而利用勾股定理得出AB的长;
(2)利用矩形性质以及坡度定义分别求出CD,CF,EF的长,进而求出梯形ABCD的周长即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 20 页 (共 21 页) 版权所有@21世纪教育网
新人教版数学九年级下册第28章28.2解直角三角形及其应用
课时作业
一、选择题
1. 如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC= ,则边BC的长为( )
A.30cm B.20cm C.10cm D.5cm
答案:C
知识点:解直角三角形
解析:解答:在直角三角形ABC中,根据三角函数定义可知:
tan∠BAC= ,又AC=30cm,tan∠BAC=,
则BC=ACtan∠BAC=30×=10cm.
故选C.
分析:此题考查学生掌握三角函数正弦、余弦及正切的定义,是一道基础题.要求注意观察生活中的数学问题,培养学生利用数学知识解决实际问题的能力,体现了数学来自于生活且服务于生活.
因为教学用的直角三角板为直角三角形,所以利用三角函数定义,一个角的正切值等于这个角的对边比邻边可知∠BAC的对边为BC,邻边为AC,根据∠BAC的正切值,即可求出BC的长度.
2. 在“测量旗杆的高度”的数学课题学习中,某学习小组测得太阳光线与水平面的夹角为27°,此时旗杆在水平地面上的影子的长度为24米,则旗杆的高度约为( )
A.24米 B. 20米 C. 16米 D. 12米
答案:D
知识点:解直角三角形的应用
解析:解答:
∵AB⊥BC,BC=24米,∠ACB=27°,
∴AB=BC·tan27°,
把BC=24米,tan27°≈0.51代入得,
AB≈24×0.51≈12米.
故选D.
分析:本题考查的是解直角三角形的应用,熟记锐角三角函数的定义是解答此题的关键.
直接根据锐角三角函数的定义可知,AB=BC·tan27°,把BC=24米,tan27°≈0.51代入进行计算即可.
3. 如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为( )
A.50米 B. 100米 C米 D. 米
答案:D
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:在Rt△ABD中,
∵∠ADB=45,°
∴BD=AB.
在Rt△ABC中,
∵∠ACB=30°,
∴=tan30°=.
∴BC=AB.
设AB=x(米),
∵CD=100,
∴BC=x+100.
∴x+100=x,
∴x=米.
故选D.
分析:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
首先根据题意分析图形;本题涉及到两个直角三角形,设AB=x(米),再利用CD=BC-BD=100的关系,进而可解即可求出答案.
4. 某水坝的坡度i=1:,坡长AB=20米,则坝的高度为( )
A.10米 B.20米 C.40米 D.20
答案:A.
知识点:解直角三角形的应用-坡度坡角问题
解析:解答:如图:
∵坡度i=1: ,
∴设AC=x,BC=x.
根据勾股定理得
AC2+BC2=AB2,
则x2+(x)2=202,
解得x=10.
故选A.
分析:此题考查了坡比的概念,不仅要熟悉解直角三角形的知识,还要熟悉勾股定理.
画出图形,根据坡度的定义__-直角三角形中,坡角的正切值,然后利用解直角三角形的知识解答.
5. 如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10米 B.10米 C.20米 D. 米
答案:A
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:∵在直角三角形ADB中,∠D=30°,
∴=tan30°,
∴BD==AB .
∴在直角三角形ABC中,∠ACB=60°.
∴BC==AB.
∵CD=20,
∴CD=BD-BC=AB-AB=20.
解得:AB=10.
故选A.
分析:本题考查仰角的定义,要求学生能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形.
首先根据题意分析图形;本题涉及到两个直角三角形,应利用其公共边AB及CD=DC-BC=20构造方程关系式,进而可解,即可求出答案.
6. 如图,某水库堤坝横断面迎水坡AB的坡比是1:,堤坝高BC=50m,则迎水坡面AB的长度是( )
A.100m B.100m C.150mD.50 m
答案:A
知识点:解直角三角形的应用-坡度坡角问题
解析:解答:∵堤坝横断面迎水坡AB的坡比是1:,
∴=.
∵BC=50m,
∴AC=50m.
∴AB==100m.
故选:A.
分析:此题主要考查了解直角三角形的应用-坡度问题,关键是掌握坡度是坡面的铅直高度h和水平宽度l的比.
根据题意可得=,把BC=50m,代入即可算出AC的长,再利用勾股定理算出AB的长即可.
7. 如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.100(+1)米
答案:D
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:由已知,得∠A=30°,∠B=45°,CD=100,
∵CD⊥AB于点D,
∴在Rt△ACD中,∠CDA=90°,tanA=.
∴AD===100.
在Rt△BCD中,∠CDB=90°,∠B=45°,
∴DB=CD=100米.
∴AB=AD+DB=100+100=100(+1)米.
故选D.
分析:本题考查了解直角三角形的应用,解决本题的关键是利用CD为直角△ABC斜边上的高,将三角形分成两个三角形,然后求解.分别在两三角形中求出AD与BD的长.
图中两个直角三角形中,都是知道已知角和对边,根据正切函数求出邻边后,相加求和即可.
8. 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有( )
A.1组 B.2组 C.3组 D.4组
答案:C
知识点:解直角三角形的应用
解析:解答:此题比较综合,要多方面考虑,
①因为知道∠ACB和BC的长,所以可利用∠ACB的正切来求AB的长;
②可利用∠ACB和∠ADB的正切求出AB;
③,因为△ABD∽△EFD可利用,求出AB;
④无法求出A,B间距离.
故共有3组可以求出A,B间距离.
故选C.
分析:本题考查相似三角形的应用和解直角三角形的应用,解答道题的关键是将实际问题转化为数学问题,本题只要把实际问题抽象到相似三角形,解直角三角形即可求出.
根据三角形相似可知,要求出AB,只需求出EF即可.所以借助于相似三角形的性质,根据即可解答.
9. 如图,△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是( )
A. B. 12 C.14 D.21
答案:A
知识点:解直角三角形的应用
解析:解答:过点A作AD⊥BC,
∵△ABC中,cosB=,sinC=,AC=5,
∴cosB==.
∴∠B=45°.
∵sinC===,
∴AD=3.
∴CD==4.
∴BD=3.
则△ABC的面积是:×AD×BC=×3×(3+4)=.
故选A.
分析:此题主要考查了解直角三角形的知识,作出AD⊥BC,进而得出相关线段的长度是解决问题的关键.
根据已知作出三角形的高线AD,进而得出AD,BD,CD,的长,即可得出三角形的面积.
10. (2011 荆州)在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )
A. B. C. D.
答案:D
知识点:解直角三角形的应用
解析:解答:
延长BA作CD⊥BD,
∵∠A=120°,AB=4,AC=2,
∴∠DAC=60°,∠ACD=30°.
∴2AD=AC=2,
∴AD=1,CD=,
∴BD=5,
∴BC=2,
∴sinB==.
故选:D.
分析:此题主要考查了解直角三角形以及勾股定理的应用,根据题意得出∠DAC=60°,∠ACD=30°是解决问题的关键.
根据∠A=120°,得出∠DAC=60°,∠ACD=30°,得出AD=1,CD=,再根据BC=2,利用解直角三角形求出.
11. 如图所示,渔船在A处看到灯塔C在北偏东60°方向上,渔船正向东方向航行了12海里到达B处,在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离是( )
A.12海里 B.6海里 C. 6海里D. 4海里
答案:D
知识点:解直角三角形的应用-方向角问题
解析:解答:由已知得:∠BAC=90°-60°=30°,
在直角三角形ABC中,
BC=ABtan30°=12×=4(海里).
故选:D.
分析:此题考查的知识点是解直角三角形的应用,关键是先得∠BAC=30°,再解直角三角形ABC即可.
此题易得∠BAC=30°,再由直角三角形ABC运用三角函数求得渔船与灯塔C的距离BC.
12. 如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于( )
A. msin米 B.mtan米 C.mcos米 D. 米
答案:B
知识点:解直角三角形的应用
解析:解答:在直角△ABC中,tan=,
∴AB=mtan.
故选B.
分析:此题考查了三角函数的基本概念,主要是正切概念及运算.
在直角△ABC中,已知∠α及其邻边,求∠α的对边,根据三角函数定义即可求解.
13. 如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
A. (+)m B. (+)m C. m D.4m
答案:A
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:∵AD=BE=5米,∠CAD=30°,
∴CD=ADtan30°=5×=(米).
∴CE=CD+DE=CD+AB=+(米).
故选A.
分析:此题主要考查学生对坡度坡角的理解及解直角三角形的综合运用能力.
应先根据相应的三角函数值算出CD长,再加上AB长即为树高.
14. 一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( )
A. (30-50,30) B. (30, 30-50)C. (30,30) D.(30, 30)
答案:A
知识点:解直角三角形的应用-方向角问题
解析:解答:过点A作AC⊥x轴于C.
在直角△OAC中,∠AOC=30°,OA=4×15=60海里,则AC=OA=30海里,OC=30海里.
因而A所在位置的坐标是(30,30).
小岛B在A的正西50海里处,因而小岛B所在位置的坐标是(30-50,30).
故选A.
分析:本题主要考查了方向角含义,正确记忆三角函数的定义是解决本题的关键.
过点A作AC⊥x轴于C,根据已知可求得点A的坐标,从而根据已知求点B的坐标.
15. 在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A、C两地的距离为( )
A. km B. km C. km D. km
答案:A
知识点:解直角三角形的应用-方向角问题
解析:解答:如图.由题意可知,AB=5km,∠2=30°,∠EAB=60°,∠3=30°.
∵EF∥PQ,
∴∠1=∠EAB=60°
又∵∠2=30°,
∴∠ABC=180°-∠1-∠2=180°-60°-30°=90°.
∴△ABC是直角三角形.
又∵MN∥PQ,
∴∠4=∠2=30°.
∴∠ACB=∠4+∠3=30°+30°=60°.
∴AC===(km).
故选A.
分析:本题是方向角问题在实际生活中的运用,解答此类题目的关键是根据题意画出图形利用解直角三角形的相关知识解答.
根据已知作图,由已知可得到△ABC是直角三角形,从而根据三角函数即可求得AC的长.
二、选择题
1. 数学实践探究课中,老师布置同学们测量学校旗杆的高度.小民所在的学习小组在距离旗杆底部10米的地方,用测角仪测得旗杆顶端的仰角为60°,则旗杆的高度是____
答案:10米
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:如图,根据题意得:AC=10米,∠ACB=60°,
∵∠A=90°,
∴在Rt△ABC中,AB=ACtan∠ACB=10×tan60°=10×=10(米).故答案为:10.
分析:本题考查仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.
由根据题意得:AC=10米,∠ACB=60°,然后再在Rt△ABC中,利用正切函数,即可求得旗杆的高度.
2. 如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是____
答案:210cm.
知识点:解直角三角形的应用-坡度坡角问题
解析:解答:过点B作BD⊥AC于D,
根据题意得:AD=2×30=60(cm),BD=18×3=54(cm),
∵斜坡BC的坡度i=1:5,
∴BD:CD=1:5,
∴CD=5BD=5×54=270(cm),
∴AC=CD-AD=270-60=210(cm).
∴AC的长度是210cm.
故答案为:210.
分析:此题考查了解直角三角形的应用:坡度问题.此题难度适中,注意掌握坡度的定义,注意数形结合思想的应用与辅助线的作法.
首先过点B作BD⊥AC于D,根据题意即可求得AD与BD的长,然后由斜坡BC的坡度i=1:5,求得CD的长,继而求得答案.
3. 如图,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°.根据图形计算tan15°=____
答案:2-.
知识点:解直角三角形的应用
解析:解答:由已知设AB=AC=2x,
∵∠A=30°,CD⊥AB,
∴CD=AC=x,
则AD2=AC2-CD2=(2x)2-x2=3x2,
∴AD=x,
∴BD=AB-AD=2x-
x=(2-)x,
∴tan15°===2-.
故答案为:2-.
分析:此题考查的知识点是解直角三角形,关键是由直角三角形中30°角的性质与勾股定理先求出CD与AD,再求出BD.
此题可设AB=AC=x,由已知可求出CD和AD,那么也能求出BD=AB-AD,从而求出tan15°.
4. 如图,为测量旗杆AB的高度,在与B距离为8米的C处测得旗杆顶端A的仰角为56°,那么旗杆的高度约是____米(结果保留整数).(参考数据:sin56°≈0.829,cos56°≈0.559,tan56°≈1.483)
答案:12
知识点:解直角三角形的应用
解析:解答:由题意知BC=8,∠C=56°,
故AB=BCtan56°≈8×1.483≈12米,
故答案为12.
分析:本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形并选择合适的边角关系求解.在直角三角形ABC中,根据BC=8,∠ACB=56°即可求得AB的长.
5. 如图,为了测量电线杆AB的高度,小明将测量仪放在与电线杆的水平距离为9m的D处.若测角仪CD的高度为1.5m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为____(精确到0.1m).(参考数据sin36°≈0.59.cos36°≈0.81,tan36°≈0.73).
答案:8.1 m.
知识点:解直角三角形的应用
解析:解答:
如图,在Rt△ACE中,
∴AE=CEtan36°
=BDtan36°
=9×tan36°
≈6.57米,
∴AB=AE+EB=AE+CD=6.57+1.5≈8.1(米).
故答案为:8.1.
分析:本题考查了三角函数在直角三角形中的运用,本题中正确计算AE的值是解题的关键.
根据CE和tan36°可以求得AE的长度,根据AB=AE+EB即可求得AB的长度,即可解题.
三、解答题
1. 为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,≈1.73,精确到个位)
答案:隧道AB的长为245m.
知识点:解直角三角形
解析:解答:
过点C作CD⊥AB于D,
∵BC=200m,∠CBA=30°,
∴在Rt△BCD中,CD=
BC=100m,BD=BCcos30°=200×=100≈173(m),
∵∠CAB=54°,
在Rt△ACD中,AD=≈≈72(m),
∴AB=AD+BD=173+72=245(m).
答:隧道AB的长为245m.
分析:此题考查了解直角三角形的应用.此题难度适中,注意掌握辅助线的作法,注意把实际问题转化为数学问题求解.
首先过点C作CD⊥AB于D,然后在Rt△BCD中,利用三角函数的知识,求得BD,CD的长,继而在Rt△ACD中,利用∠CAB的正切求得AD的长,继而求得答案.
2. 如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.(取1.73,结果保留整数.)
答案:建筑物CD的高约为47 m.
知识点:解直角三角形的应用-仰角俯角问题
解析:解答:
过点P作PE⊥CD于E,则四边形BCEP是矩形.
∴PE=BC=30.
在Rt△PDE中,∵∠DPE=30°,PE=30,
∴DE=PE×tan30°=30×=10.
在Rt△PEC中,∵∠EPC=45°,PE=30,
∴CE=PE×tan45°=30×1=30.
∴CD=DE﹢CE=30﹢10=30﹢17.3≈47(m)
答:建筑物CD的高约为47 m.
分析:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
过点P作PE⊥CD于E,则四边形BCEP是矩形,得到PE=BC=30,在Rt△PDE中,利用∠DPE=30°,PE=30,求得DE的长;在Rt△PEC中,利用∠EPC=45°,PE=30求得CE的长,利用CD=DE﹢CE即可求得结果.
3. 如图,在Rt△ABC中,∠ACB=90°,已知CD⊥AB,BC=1
(1)如果∠BCD=30°,求AC;
(2)如果tan∠BCD=,求CD.
答案:(1)AC=;(2)CD=
知识点:解直角三角形
解析:解答:(1)∵CD⊥AB,∴∠BDC=90°,
∵∠DCB=30°,∴∠B=60°,
在Rt△ACB中,∠ACB=90°,
∴tan60°==,又BC=1,
则AC=;
(2)在Rt△BDC中,tan∠BCD==,
设BD=k,则CD=3k,又BC=1,
利用勾股定理得:k2+(3k)2=1,
解得:k=或k=-(舍去),
则CD=3k=.
分析:此题属于解三角形的题型,涉及的知识有:勾股定理,锐角三角函数定义,比例的性质,以及特殊角的三角函数值,是一道多知识点的综合题.
(1)根据直角三角形的两锐角互余,由∠BCD的度数求出∠B的度数,利用锐角三角函数定义表示出tanB,将tanB及BC的长代入,即可求出AC的长;
(2)在直角三角形BDC中,由已知tan∠BCD的值,利用锐角三角函数定义得出BD与CD的比值为1:3,根据比值设出BD=k,CD=3k,再由BC的长,利用勾股定理列出关于k的方程,求出方程的解得到k的值,即可求出CD的长.
4. 如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据≈1.41,≈1.73)
答案:A、C之间的距离为10.3海里.
知识点:解直角三角形的应用-方向角问题
解析:解答:
作AD⊥BC,垂足为D,
由题意得,∠ACD=45°,∠ABD=30°,
设CD=x,在Rt△ACD中,可得AD=x,
在Rt△ABD中,可得BD=x,
又∵BC=20,即x+x=20,解得:x=10(-1)
∴AC=x≈10.3(海里).
答:A、C之间的距离为10.3海里.
分析:此题考查了解直角三角形的应用,解答本题的关键是根据题意构造直角三角形,将实际问题转化为数学模型进行求解,难度一般.
作AD⊥BC,垂足为D,设CD=x,利用解直角三角形的知识,可得出AD,继而可得出BD,结合题意BC=CD+BD=20海里可得出方程,解出x的值后即可得出答案.
5. 如图,拦水坝的横断面为梯形ABCD,坝顶宽AD=5米,斜坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
(1)求斜坡AB的长;
(2)求拦水坝的横断面梯形ABCD的周长.(注意:本题中的计算过程和结果均保留根号)
答案:(1)斜坡AB的长为6m;(2)拦水坝的横断面梯形ABCD的周长为(37+6
+3)m.
知识点:解直角三角形的应用-坡度坡角问题
解析:解答:
(1)∵=i=,AE=6,
∴BE=3AE=18,在Rt△ABE中,根据勾股定理得: AB=
=6,
答:斜坡AB的长为6m;
(2)过点D作DF⊥BC于F,
可得四边形AEFD是矩形,
故EF=AD,∵AD=5,∴EF=5,
∵=i=,
DF=AE=6,
∴CF=DF=9,
∴BC=BE+EF+CF=18+5+9=32,
在Rt△DCF中,根据勾股定理得:
DC=
=3,
∴梯形ABCD的周长为:AB+BC+CD+DA=6+32+3+5=37+6+3,
答:拦水坝的横断面梯形ABCD的周长为(37+6
+3)m.
分析:此题主要考查了坡度的定义以及勾股定理的应用,根据已知坡度定义得出BE,FC的长是解题关键.
(1)根据坡度的定义得出BE的长,进而利用勾股定理得出AB的长;
(2)利用矩形性质以及坡度定义分别求出CD,CF,EF的长,进而求出梯形ABCD的周长即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 20 页 (共 21 页) 版权所有@21世纪教育网
