海南省东方市两校2023-2024学年九年级下学期入学考试数学试卷(无答案)
文档属性
| 名称 | 海南省东方市两校2023-2024学年九年级下学期入学考试数学试卷(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 399.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 11:59:13 | ||
图片预览

文档简介
东方市两校2023年春季入学考试
初三数学试卷
选择题:(本大题满分36分,每小题3分)
1.实数-3的倒数是( )
A. 3 B.-3 C. D.
2.海南日报记者从海口海关获悉,据统计,今年元旦假期(2022年12月31日至2023年1月2日),该关共监管离岛免税购物旅客43000人次,逐步恢复到去年元旦假期水平。将数据43000用科学记数法表示为( )
A. B. C. D.
3.由五个大小相同的正方体搭成的几何体如图所示,从左面看该几何
体的形状图是( )
A.B.C. D.
4.下列运算正确的是( )
A. B. C. D.
5.如图,是的外角的平分线,若, ,则( )
A.35° B.40° C.45° D.55°
6.方程解是( ).
A. B. C. D.
7. 中考体育科目实行新政策,引体向上成为男生自主选考科目之一.现有六位初三男生引体向上成绩如下:7,3,11,8,2,8(单位:个),这些成绩的中位数和众数分别是( )
A.7,8 B.7.5,8 C.9.5,8 D.7.5,16
如图,已知△ABC,按以下步骤作图:①分别以B、C为圆心,以大于BC的长为半径作弧两弧相交于两点M、N;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=65°,则∠ACD的度数为( )
A.65° B.60° C.55° D.45°
9.已知a、b表示下表第一行中两个相邻的数,且a<<b,那么a的值是( )
x 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4
x2 9 9.61 10.24 10.89 11.56 12.25 12.96 13.69 14.44 15.21 16
A.3.5 B.3.6 C.3.7 D.3.8
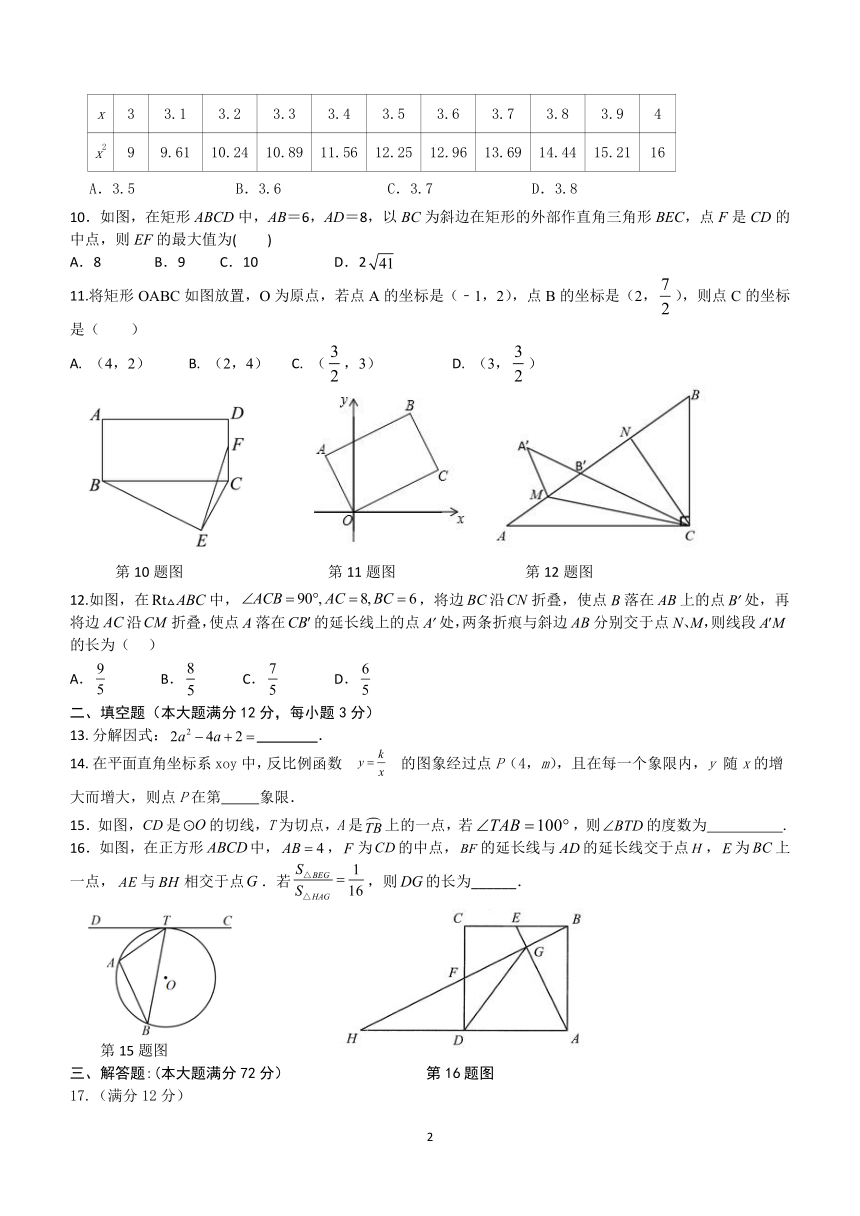
10.如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A.8 B.9 C.10 D.2
11.将矩形OABC如图放置,O为原点,若点A的坐标是(﹣1,2),点B的坐标是(2,),则点C的坐标是( )
A. (4,2) B. (2,4) C. (,3) D. (3,)
第10题图 第11题图 第12题图
12.如图,在中,,将边沿折叠,使点B落在上的点处,再将边沿折叠,使点A落在的延长线上的点处,两条折痕与斜边分别交于点N、M,则线段的长为( )
A. B. C. D.
填空题(本大题满分12分,每小题3分)
分解因式: .
在平面直角坐标系xoy中,反比例函数 的图象经过点P(4,m),且在每一个象限内,y 随x的增大而增大,则点P在第 象限.
15.如图,是的切线,T为切点,A是上的一点,若,则的度数为 .
16.如图,在正方形中,,为的中点,的延长线与的延长线交于点,为上一点,与相交于点.若,则的长为______.
第15题图
解答题:(本大题满分72分) 第16题图
17.(满分12分)
(2) 解不等式组:.
18.(满分10分)初中生涯即将结束,同学们为友谊长存,决定互送礼物,于是去某礼品店购进了一批适合学生的毕业纪念品.已知购进3个A种礼品和2个B种礼品共需54元,购进3个A种礼品比购进5个B种礼品多花12元.问A,B两种礼品每个的进价是多少元?
19(满分10分).如今很多初中生购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:
A:自带白开水;B:瓶装矿泉水;C:碳酸饮料;D:非碳酸饮料
根据统计结果绘制如下两个统计图和统计表,根据统计图提供的信息,解答下列问题:
饮品名称 自带白开水 瓶装矿泉水 碳酸饮料 非碳酸饮料
平均(元/瓶) 0 2 3 4
这个班级有 名同学;扇形统计图中B所对应扇形的圆心角是 度。
若该班同学每人每天只饮用一种饮品(每种仅限1瓶,价格见表格),则该班同学每天用于饮品上的人均花费是 元;
为了养成良好的生活习惯,班主任决定在自带白开水的5名同学(男生2人,女生3人)中随机抽取2名同学做良好习惯监督员,则恰好抽到2名女生的概率是 .
若该校有2000名学生,则估计每天引用碳酸饮料的有 名学生。
20.(满分10分)如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C处遇险发出求救信号,此时测得C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,测得C点与观测点A的距离为25海里.
(1)如图填空:∠CBD= 度;
(2)求观测点B与C之间的距离;
(3)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.
21.(满分15分)如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)求证:CE=CF;
(2)若∠ABC=120°,连结BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
22.(满分15分)已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C.顶点为点D.点P为抛物线上的一个动点。
(1)求抛物线的解析式;
(2)若过点C的直线交线段AB于点E,且
S△ACE:S△CEB=3:5,求线段CE的长是多少?
(3) 当点P在第一象限时,连接PC和PB,求△PBC面积的最大 值时多少?
(4)若点Q在x轴上,当以点D,C,P,Q为顶点的四边形是平行四边形时,请直接写出点P的坐标.
初三数学试卷
选择题:(本大题满分36分,每小题3分)
1.实数-3的倒数是( )
A. 3 B.-3 C. D.
2.海南日报记者从海口海关获悉,据统计,今年元旦假期(2022年12月31日至2023年1月2日),该关共监管离岛免税购物旅客43000人次,逐步恢复到去年元旦假期水平。将数据43000用科学记数法表示为( )
A. B. C. D.
3.由五个大小相同的正方体搭成的几何体如图所示,从左面看该几何
体的形状图是( )
A.B.C. D.
4.下列运算正确的是( )
A. B. C. D.
5.如图,是的外角的平分线,若, ,则( )
A.35° B.40° C.45° D.55°
6.方程解是( ).
A. B. C. D.
7. 中考体育科目实行新政策,引体向上成为男生自主选考科目之一.现有六位初三男生引体向上成绩如下:7,3,11,8,2,8(单位:个),这些成绩的中位数和众数分别是( )
A.7,8 B.7.5,8 C.9.5,8 D.7.5,16
如图,已知△ABC,按以下步骤作图:①分别以B、C为圆心,以大于BC的长为半径作弧两弧相交于两点M、N;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=65°,则∠ACD的度数为( )
A.65° B.60° C.55° D.45°
9.已知a、b表示下表第一行中两个相邻的数,且a<<b,那么a的值是( )
x 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4
x2 9 9.61 10.24 10.89 11.56 12.25 12.96 13.69 14.44 15.21 16
A.3.5 B.3.6 C.3.7 D.3.8
10.如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A.8 B.9 C.10 D.2
11.将矩形OABC如图放置,O为原点,若点A的坐标是(﹣1,2),点B的坐标是(2,),则点C的坐标是( )
A. (4,2) B. (2,4) C. (,3) D. (3,)
第10题图 第11题图 第12题图
12.如图,在中,,将边沿折叠,使点B落在上的点处,再将边沿折叠,使点A落在的延长线上的点处,两条折痕与斜边分别交于点N、M,则线段的长为( )
A. B. C. D.
填空题(本大题满分12分,每小题3分)
分解因式: .
在平面直角坐标系xoy中,反比例函数 的图象经过点P(4,m),且在每一个象限内,y 随x的增大而增大,则点P在第 象限.
15.如图,是的切线,T为切点,A是上的一点,若,则的度数为 .
16.如图,在正方形中,,为的中点,的延长线与的延长线交于点,为上一点,与相交于点.若,则的长为______.
第15题图
解答题:(本大题满分72分) 第16题图
17.(满分12分)
(2) 解不等式组:.
18.(满分10分)初中生涯即将结束,同学们为友谊长存,决定互送礼物,于是去某礼品店购进了一批适合学生的毕业纪念品.已知购进3个A种礼品和2个B种礼品共需54元,购进3个A种礼品比购进5个B种礼品多花12元.问A,B两种礼品每个的进价是多少元?
19(满分10分).如今很多初中生购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:
A:自带白开水;B:瓶装矿泉水;C:碳酸饮料;D:非碳酸饮料
根据统计结果绘制如下两个统计图和统计表,根据统计图提供的信息,解答下列问题:
饮品名称 自带白开水 瓶装矿泉水 碳酸饮料 非碳酸饮料
平均(元/瓶) 0 2 3 4
这个班级有 名同学;扇形统计图中B所对应扇形的圆心角是 度。
若该班同学每人每天只饮用一种饮品(每种仅限1瓶,价格见表格),则该班同学每天用于饮品上的人均花费是 元;
为了养成良好的生活习惯,班主任决定在自带白开水的5名同学(男生2人,女生3人)中随机抽取2名同学做良好习惯监督员,则恰好抽到2名女生的概率是 .
若该校有2000名学生,则估计每天引用碳酸饮料的有 名学生。
20.(满分10分)如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C处遇险发出求救信号,此时测得C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,测得C点与观测点A的距离为25海里.
(1)如图填空:∠CBD= 度;
(2)求观测点B与C之间的距离;
(3)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.
21.(满分15分)如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)求证:CE=CF;
(2)若∠ABC=120°,连结BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
22.(满分15分)已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C.顶点为点D.点P为抛物线上的一个动点。
(1)求抛物线的解析式;
(2)若过点C的直线交线段AB于点E,且
S△ACE:S△CEB=3:5,求线段CE的长是多少?
(3) 当点P在第一象限时,连接PC和PB,求△PBC面积的最大 值时多少?
(4)若点Q在x轴上,当以点D,C,P,Q为顶点的四边形是平行四边形时,请直接写出点P的坐标.
同课章节目录
