物理人教版(2019)必修第二册6.1圆周运动(共32张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册6.1圆周运动(共32张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 43.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-02 13:18:27 | ||
图片预览









文档简介
(共32张PPT)
第六章圆周运动
6.1 圆周运动
复习回顾:
1、什么是斜抛运动?如何求斜抛运动的速度和位移?
2、斜抛运动的哪三个量实对称的?
3、什么是类平抛运动?
4、处理类平抛运动的一般方法?
5、斜面抛的五种类型是什么?
6、与圆结合的平抛运动问题的三种类型?
7、竖直墙面的平抛运动?
8、平抛运动的临界问题?
9、平抛运动的相遇问题?
除了摩天轮的运动,生活中还有很多物体,或物体的一部分做圆周运动,例如:
那么什么叫圆周运动?用哪些量来描述匀周运动?这些量之间有什么关系?如何比较做圆周运动的快慢呢?这就是这一节我们要学的问题。
1.定义:质点的运动轨迹是圆或圆的一部分的运动叫做圆周运动。
如何比较圆周运动的快慢?
一、圆周运动
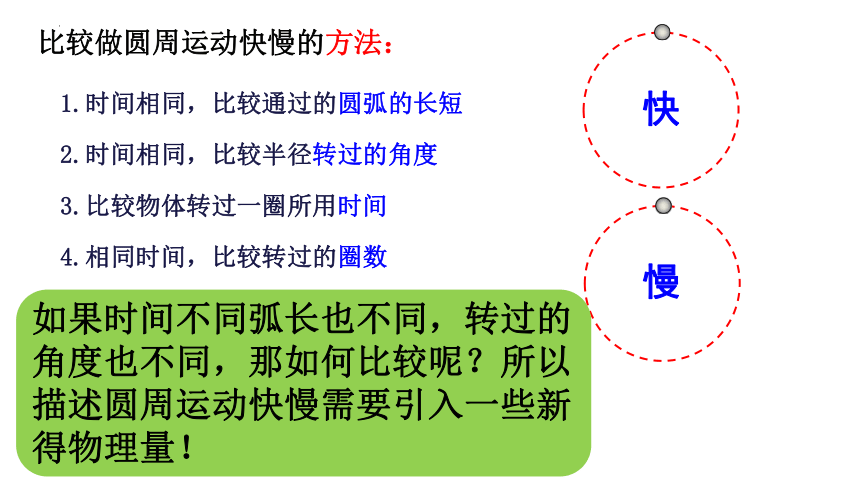
比较做圆周运动快慢的方法:
1.时间相同,比较通过的圆弧的长短
2.时间相同,比较半径转过的角度
3.比较物体转过一圈所用时间
4.相同时间,比较转过的圈数
慢
快
如果时间不同弧长也不同,转过的角度也不同,那如何比较呢?所以描述圆周运动快慢需要引入一些新得物理量!
s
二、线速度
A
B
t
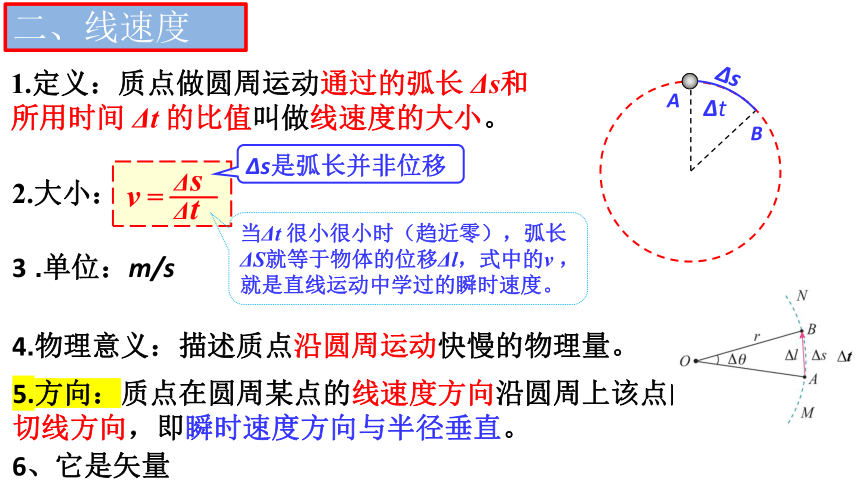
1.定义:质点做圆周运动通过的弧长 Δs和所用时间 Δt 的比值叫做线速度的大小。
2.大小:
v =
Δt
Δs
Δs是弧长并非位移
4.物理意义:描述质点沿圆周运动快慢的物理量。
3 .单位:m/s
5.方向:质点在圆周某点的线速度方向沿圆周上该点的切线方向,即瞬时速度方向与半径垂直。
当Δt 很小很小时(趋近零),弧长ΔS就等于物体的位移Δl,式中的v ,就是直线运动中学过的瞬时速度。
6、它是矢量
7.线速度一般指某一时刻或某一刻的瞬时速度
v
v
v
o
:物体做圆周运动的线速度的大小处处相等
8.匀速圆周运动
【问题】匀速圆周运动中的“匀速”指速度不变吗?
率
匀速圆周运动的线速度方向是在时刻变化的, 因此它是一种变速运动,这里的“匀速”是指速率不变。
9、匀速圆周运动是一种变加速曲线运动。
加速度方向时刻在变化
判断:
1、匀速圆周运动是匀速运动。( )
2、匀速圆周运动是线速度不变的运动。( )
3、匀速圆周运动相等时间内走过的位移相同。( )
4、匀速圆周运动相等时间内走过的路程相同。( )
5、匀速圆周运动相等时间内平均速度相同。( )
做一做
√
×
×
×
×
05.
在赤道A点的人和在北纬60°上B点的人随地球转动一周,相等时间内它们转过的角度相同,但转过的弧长却不同。
看来只用线速度描述圆周运动不能全面说明问题。我们该如何描述这种相同和不同呢?
Δθ
A
B
t
1、定义:
质点与圆心的连线扫过的角度Δθ跟所用时间Δt的比值。
2. 大小:
ω=
Δt
Δ
θ
Δθ采用弧度制
3.单位:
rad/s(弧度/秒)或s-1
4.物理意义:
描述物体绕圆心转动的快慢
5.是 (高中不研究方向。)
矢量
6.匀速圆周运动的角速度是不变的,但是线速度却是变化的。
三、角速度
温馨提示(回顾数学知识):
圆心角 θ的国际单位:
弧度(rad)
练习:1800对应多少弧度? 900对应多少弧度?
【例题1】关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀速运动
B.匀速圆周运动是角速度不变的运动
C.匀速圆周运动是线速度不变的运动
D.匀速圆周运动是加速度不变的运动
B
还有其他描述圆周运动快慢
的方法吗?
定义
符号
单位
物理意义 关系 物体在单位时间(每秒或每分)转的圈数
n
r/s或r/min
描述物体做圆周运动的快慢
物体运动一周所用的时间
物体在单位时间(每秒)转的圈数
T
f
s
Hz或s-1
n = f =
T
1
转速
周期
频率
频率越高f表明物体运转得越快!
转速n越大表明物体运动得越快!
周期T越短表明物体运转得越快!
当转速的单位取r/s时,n与f含义相同,n在工程技术常用
四、周期频率和转速
2、匀速圆周运动是周期、频率、转速、线速度大小、角速度都不变的运动!
s
【思考】线速度、角速度与周期T(频率f或转速n)的关系?
①与T的关系:
②与T的关系:
③与的关系:
1、半径一定,线速度与角速度成正比
2、角速度一定,线速度与半径成正比
3、线速度一定,角速度与半径成反比
五、各物理量之间的关系
v =
Δt
Δs
ω=
Δt
Δ
θ
v = ωr
记一记
2、同轴转动:各点的角速度(周期、频率、转速)相等。
1、皮带、链条、齿轮、静摩擦传动:边缘点线速等
六、几种常见的传动装置
对自行车上三个轮转动的描述
C
B
A
1.A、B的线速度相同
2.B、C的角速度相同
3.B、C比A角速度大
4.C比A、B线速度大
04.
【例题2】如图,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮半径的2倍,它们之间靠摩擦传动,接触面不打滑。下列说法正确的是( )
A.A与B线速度大小相等
B.B与C线速度大小相等
C.A的角速度是C的2倍
D.A与C线速度大小相等
A
【例题3】如图所示的皮带传动装置,主动轮O1上两轮的半径分别为3r和,从动轮O2的半径为2r,A、B、C分别为转轮缘上的三点,设皮带不打滑,求:
(1)A、B、C 三点的线速度大小之比为多少?
(2)A、B、C 三点的角速度之比为多少?
r
3r
2r
3:1:1
2:2:1
【例题4】如图为地球自转的示意图,图中A点位移赤道、B、C分别位移北纬300和600,则
ωA: ωB :ωc=___________;
vA: vB :vc=____________;
R
A
B
C
O
赤道
地轴
1:1:1
【例题5】(单)如图所示的齿轮传动装置中,主动轮和从动轮的齿大小相同,主动轮的齿数z1=24,从动轮的齿数z2=8,若已知主动轮以角速度ω顺时针转动时,则从动轮的运动情况是( )
A.顺时针转动,周期为2π/3ω
B.逆时针转动,周期为2π/3ω
C.顺时针转动,周期为6π/ω
D.逆时针转动,周期为6π/ω
B
齿轮传动:齿数之比等于半径之比
【例题6】(2022秋·江苏苏州·高三期中)学校门口的车牌自动识别系统如图所示,闸杆转轴O与车左侧面水平距离为0.6m,闸杆距地面高为1m,可绕转轴O在竖直面内匀速转动,其角速度为 。汽车以速度3m/s匀速驶入自动识别区,识别的反应时间为0.3s。若汽车可看成高1.6m的长方体,要使汽车匀速顺利通过,则自动识别区
ab到 的距离至少为( )
A.6.9m B.7.0m
C.7.2m D.7.6m
A
【例题7】(2022春·广西河池·高一阶段练习)如图所示,如果把钟表上的时针、分针、秒针的运动看成匀速转动,那么从它的分针与时针第一次重合至第二次重合,中间经历的时间为( )
A.1h B. h
C. h D. h
C
【例题8】如图所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,在其正上方高h处沿OB方向水平抛出一小球,不计空气阻力,重力加速度为g,要使球与盘只碰一次,且落点为B,B为圆盘边缘上的点,求小球的初速度v的大小及圆盘转动的角速度ω。
课堂小结
线速度
角速度
周期
关系
质点做圆周运动通过的弧长 Δs和所用时间 Δt 的比值叫做线速度。
物体做圆周运动,连接物体和圆心的半径转过的角度Δθ和所用时间Δt的比值叫做角速度。
周期:T
频率:f
转速:n
第六章圆周运动
6.1 圆周运动
复习回顾:
1、什么是斜抛运动?如何求斜抛运动的速度和位移?
2、斜抛运动的哪三个量实对称的?
3、什么是类平抛运动?
4、处理类平抛运动的一般方法?
5、斜面抛的五种类型是什么?
6、与圆结合的平抛运动问题的三种类型?
7、竖直墙面的平抛运动?
8、平抛运动的临界问题?
9、平抛运动的相遇问题?
除了摩天轮的运动,生活中还有很多物体,或物体的一部分做圆周运动,例如:
那么什么叫圆周运动?用哪些量来描述匀周运动?这些量之间有什么关系?如何比较做圆周运动的快慢呢?这就是这一节我们要学的问题。
1.定义:质点的运动轨迹是圆或圆的一部分的运动叫做圆周运动。
如何比较圆周运动的快慢?
一、圆周运动
比较做圆周运动快慢的方法:
1.时间相同,比较通过的圆弧的长短
2.时间相同,比较半径转过的角度
3.比较物体转过一圈所用时间
4.相同时间,比较转过的圈数
慢
快
如果时间不同弧长也不同,转过的角度也不同,那如何比较呢?所以描述圆周运动快慢需要引入一些新得物理量!
s
二、线速度
A
B
t
1.定义:质点做圆周运动通过的弧长 Δs和所用时间 Δt 的比值叫做线速度的大小。
2.大小:
v =
Δt
Δs
Δs是弧长并非位移
4.物理意义:描述质点沿圆周运动快慢的物理量。
3 .单位:m/s
5.方向:质点在圆周某点的线速度方向沿圆周上该点的切线方向,即瞬时速度方向与半径垂直。
当Δt 很小很小时(趋近零),弧长ΔS就等于物体的位移Δl,式中的v ,就是直线运动中学过的瞬时速度。
6、它是矢量
7.线速度一般指某一时刻或某一刻的瞬时速度
v
v
v
o
:物体做圆周运动的线速度的大小处处相等
8.匀速圆周运动
【问题】匀速圆周运动中的“匀速”指速度不变吗?
率
匀速圆周运动的线速度方向是在时刻变化的, 因此它是一种变速运动,这里的“匀速”是指速率不变。
9、匀速圆周运动是一种变加速曲线运动。
加速度方向时刻在变化
判断:
1、匀速圆周运动是匀速运动。( )
2、匀速圆周运动是线速度不变的运动。( )
3、匀速圆周运动相等时间内走过的位移相同。( )
4、匀速圆周运动相等时间内走过的路程相同。( )
5、匀速圆周运动相等时间内平均速度相同。( )
做一做
√
×
×
×
×
05.
在赤道A点的人和在北纬60°上B点的人随地球转动一周,相等时间内它们转过的角度相同,但转过的弧长却不同。
看来只用线速度描述圆周运动不能全面说明问题。我们该如何描述这种相同和不同呢?
Δθ
A
B
t
1、定义:
质点与圆心的连线扫过的角度Δθ跟所用时间Δt的比值。
2. 大小:
ω=
Δt
Δ
θ
Δθ采用弧度制
3.单位:
rad/s(弧度/秒)或s-1
4.物理意义:
描述物体绕圆心转动的快慢
5.是 (高中不研究方向。)
矢量
6.匀速圆周运动的角速度是不变的,但是线速度却是变化的。
三、角速度
温馨提示(回顾数学知识):
圆心角 θ的国际单位:
弧度(rad)
练习:1800对应多少弧度? 900对应多少弧度?
【例题1】关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀速运动
B.匀速圆周运动是角速度不变的运动
C.匀速圆周运动是线速度不变的运动
D.匀速圆周运动是加速度不变的运动
B
还有其他描述圆周运动快慢
的方法吗?
定义
符号
单位
物理意义 关系 物体在单位时间(每秒或每分)转的圈数
n
r/s或r/min
描述物体做圆周运动的快慢
物体运动一周所用的时间
物体在单位时间(每秒)转的圈数
T
f
s
Hz或s-1
n = f =
T
1
转速
周期
频率
频率越高f表明物体运转得越快!
转速n越大表明物体运动得越快!
周期T越短表明物体运转得越快!
当转速的单位取r/s时,n与f含义相同,n在工程技术常用
四、周期频率和转速
2、匀速圆周运动是周期、频率、转速、线速度大小、角速度都不变的运动!
s
【思考】线速度、角速度与周期T(频率f或转速n)的关系?
①与T的关系:
②与T的关系:
③与的关系:
1、半径一定,线速度与角速度成正比
2、角速度一定,线速度与半径成正比
3、线速度一定,角速度与半径成反比
五、各物理量之间的关系
v =
Δt
Δs
ω=
Δt
Δ
θ
v = ωr
记一记
2、同轴转动:各点的角速度(周期、频率、转速)相等。
1、皮带、链条、齿轮、静摩擦传动:边缘点线速等
六、几种常见的传动装置
对自行车上三个轮转动的描述
C
B
A
1.A、B的线速度相同
2.B、C的角速度相同
3.B、C比A角速度大
4.C比A、B线速度大
04.
【例题2】如图,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮半径的2倍,它们之间靠摩擦传动,接触面不打滑。下列说法正确的是( )
A.A与B线速度大小相等
B.B与C线速度大小相等
C.A的角速度是C的2倍
D.A与C线速度大小相等
A
【例题3】如图所示的皮带传动装置,主动轮O1上两轮的半径分别为3r和,从动轮O2的半径为2r,A、B、C分别为转轮缘上的三点,设皮带不打滑,求:
(1)A、B、C 三点的线速度大小之比为多少?
(2)A、B、C 三点的角速度之比为多少?
r
3r
2r
3:1:1
2:2:1
【例题4】如图为地球自转的示意图,图中A点位移赤道、B、C分别位移北纬300和600,则
ωA: ωB :ωc=___________;
vA: vB :vc=____________;
R
A
B
C
O
赤道
地轴
1:1:1
【例题5】(单)如图所示的齿轮传动装置中,主动轮和从动轮的齿大小相同,主动轮的齿数z1=24,从动轮的齿数z2=8,若已知主动轮以角速度ω顺时针转动时,则从动轮的运动情况是( )
A.顺时针转动,周期为2π/3ω
B.逆时针转动,周期为2π/3ω
C.顺时针转动,周期为6π/ω
D.逆时针转动,周期为6π/ω
B
齿轮传动:齿数之比等于半径之比
【例题6】(2022秋·江苏苏州·高三期中)学校门口的车牌自动识别系统如图所示,闸杆转轴O与车左侧面水平距离为0.6m,闸杆距地面高为1m,可绕转轴O在竖直面内匀速转动,其角速度为 。汽车以速度3m/s匀速驶入自动识别区,识别的反应时间为0.3s。若汽车可看成高1.6m的长方体,要使汽车匀速顺利通过,则自动识别区
ab到 的距离至少为( )
A.6.9m B.7.0m
C.7.2m D.7.6m
A
【例题7】(2022春·广西河池·高一阶段练习)如图所示,如果把钟表上的时针、分针、秒针的运动看成匀速转动,那么从它的分针与时针第一次重合至第二次重合,中间经历的时间为( )
A.1h B. h
C. h D. h
C
【例题8】如图所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,在其正上方高h处沿OB方向水平抛出一小球,不计空气阻力,重力加速度为g,要使球与盘只碰一次,且落点为B,B为圆盘边缘上的点,求小球的初速度v的大小及圆盘转动的角速度ω。
课堂小结
线速度
角速度
周期
关系
质点做圆周运动通过的弧长 Δs和所用时间 Δt 的比值叫做线速度。
物体做圆周运动,连接物体和圆心的半径转过的角度Δθ和所用时间Δt的比值叫做角速度。
周期:T
频率:f
转速:n
