初中数学人教版九年级下册 27.1图形的相似课件(第1-2课时) 31张PPT
文档属性
| 名称 | 初中数学人教版九年级下册 27.1图形的相似课件(第1-2课时) 31张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
第二十七章
相似
九年级数学人教版·下册
27.1 图形的相似
第一课时
相似图形
教学目标
1.理解并掌握相似图形的概念及特征;(重点)
2.理解相似图形的特征,掌握识别相似图形的方法.(难点)
全等图形
指能够完全重合的两个图形,
即它们的形状和大小完全相同.
新课导入
新课导入
四阶魔方和三阶魔方形状相同吗?大小呢?
新课导入
问题1:图中的两个图形有什么关系?
它们还全等吗?
什么样的图形是全等图形?
形状相同,大小也相同.
不全等.形状相同,大小不相同.
全等.
新知探究
两个图形的形状完全相同 ,但图形的大小位置不一定相同,这样的图形叫做相似图形.
新知探究
新知探究
我们把形状相同的图形叫相似图形.
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
相似图形:
全等图形是相似图形,
相似图形不一定是全等图形.
新知探究
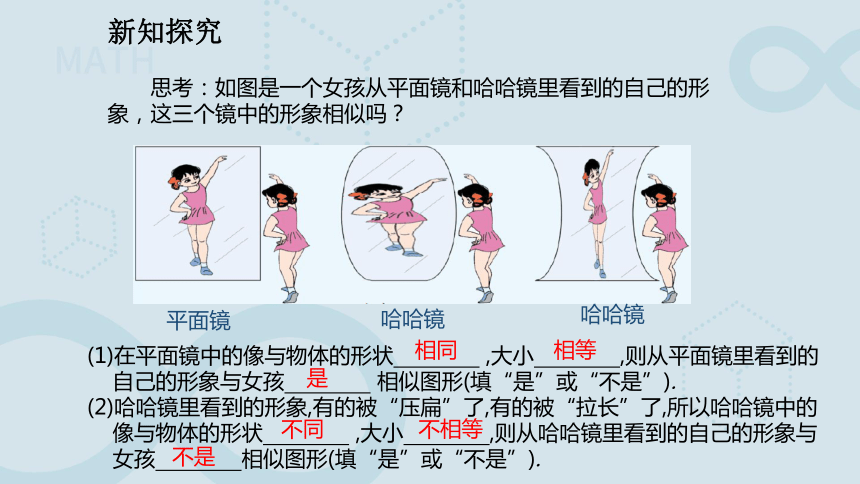
思考:如图是一个女孩从平面镜和哈哈镜里看到的自己的形象,这三个镜中的形象相似吗?
哈哈镜
平面镜
哈哈镜
(1)在平面镜中的像与物体的形状 ,大小 ,则从平面镜里看到的
自己的形象与女孩 相似图形(填“是”或“不是”).
(2)哈哈镜里看到的形象,有的被“压扁”了,有的被“拉长”了,所以哈哈镜中的
像与物体的形状 ,大小 ,则从哈哈镜里看到的自己的形象与
女孩 相似图形(填“是”或“不是”).
相同
相等
是
不同
不相等
不是
1.如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
相似
新知探究
新知探究
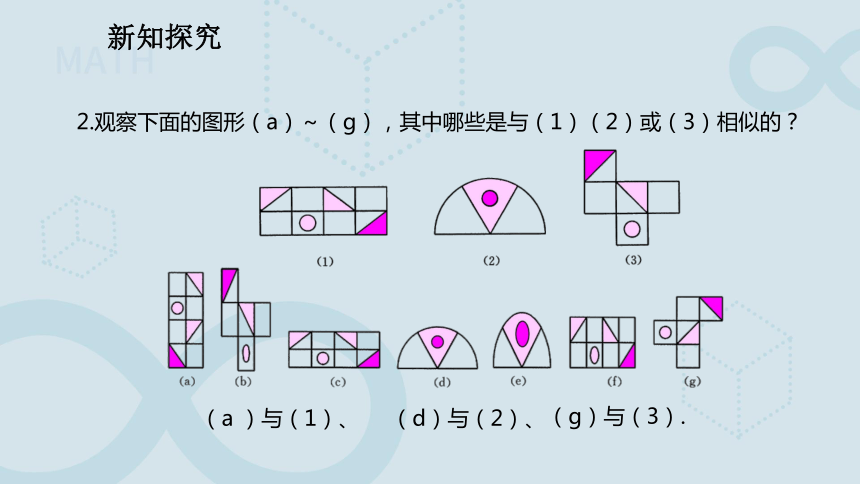
2.观察下面的图形(a)~(g),其中哪些是与(1)(2)或(3)相似的?
(a )与(1)、
(d)与(2)、
(g)与(3).
课堂小结
相似图形
两个图形的形状完全相同.
但图形的大小位置不一定相同.
课堂小测
1.下列四个命题:①所有的直角三角形都相似;②所有的等腰三角形都相似;
③所有的正方形都相似;④所有的菱形都相似.其中正确的有 ( )
A.2个 B.3个 C.4个 D.1个
D
2.下列图形是相似图形的是 ( )
A.①②③ B.②③④ C.①③④ D.①②④
A
课堂小测
3.下列图形不是相似图形的是 ( )
A.同一张底片冲洗出来的两张大小不同的照片
B.用放大镜将一个细小物体图案放大过程中原有图案和放大图案
C.某人的侧身照片和正面照片
D.大小不同的两张中国地图
C
课堂小测
4.想一想
(1)所有的圆都是相似图形吗?
(2)所有的等边三角形都是相似图形吗?
(3)所有的三角形都是相似图形吗?
(4)所有的正方形都是相似图形吗?
(5)所有的长方形都是相似图形吗?
是
是
不是
是
不是
第二课时
相似多边形
教学目标
1.理解并掌握相似多边形的概念及性质;(重点)
2.能利用成比例线段的概念及相似多边形的性质进行有关计算.(难点)
新课导入
将△ABC用2倍放大镜观察得到△A1B1C1,这两个三角形相似吗
这两个三角形中的对应角、对应边之间有什么关系
相似.
对应的角相等,对应的边成比例.
如图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形.
对于图中两个相似的四边形,它们的对应角,对应边的比是否相等?
相等
新知探究
新知探究
定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
相似比:相似多边形对应边的比叫做相似比,全等是相似比等于1的特殊情况.
符号语言(以四边形为例):
∵四边形ABCD∽四边形A′B′C′D′
(相似多边形的对应边成比例,对应角相等)
新知探究
例题 如图,四边形ABCD和EFGH相似,求∠α、∠ β的大小和EH的长度x.
24cm
x
解:
∵四边形ABCD和EFGH相似,
∴∠α=∠C=83 °,∠A=∠E=118 °.
118°
在四边形ABCD中
∠ β= 360°-( 78°+ 83°+ 118° )=81 °.
∵四边形ABCD和EFGH相似 ,
∴
,即
∴x=28(cm).
,
如图,矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所成的矩形EFGH和矩形ABCD是否相似
A
F
E
H
G
D
C
B
∴不相似
新知探究
新知探究
成比例线段:对于四条线段a,b,c,d,如果其中两条线段的比与另外两条线段的比相等,如 (即ad=bc),我们就说这四条线段成比例.
1.已知a,b,c,d是成比例线段,且a=3 cm,b=2 cm,c=6 cm,则d= cm.
2.在比例尺为1∶6000000的地图上,量得南京到北京的距离是15 cm,则这两地的实际距离是 km.
4
900
新知探究
课堂小结
相似多边形
定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
相似比:相似多边形对应边的比叫做相似比,全等是相似比等于1的特殊情况.
成比例线段:对于四条线段a,b,c,d,如果其中两条线段的比与另外两条线段的比相等,如 (即ad=bc),我们就说这四条线段成比例.
1、填空:
(1)等腰三角形两腰的比是________;
(2)直角三角形斜边上的中线和斜边的比是_________.
1∶1
1∶2
课堂小测
2、填空:
(1)如图①,则x= ,y = ,α= ;
(2)如图②,x= .
╯
80°
╰
65°
╯
80°
╮
125°
α
╭
3
6
x
y
图①
3
5
30
20
15
x
图②
2.5
1.5
90°
22.5
课堂小测
课堂小测
3、在两个相似的五边形中,一个五边形各边长分别为1,2,3,4,5,另
一个五边形最大边为10,则最短的边为( )
A. 2 B. 4 C. 6 D. 8
A
4、△ABC与△DEF相似,且相似比是 ,则△DEF与△ABC的相似比是( )
A. B. C. D.
B
5、 五边形ABCDE相似于五边形A′B′C′D′E′,它们的相似比为1 : 3.
(1)若∠D=135°,则∠D′= ______;
(2)若A′B′=15,则AB= ______.
135°
5
6、一个多边形的边长分别是2、3、4、5、6,另一个和它相似的 多边形的最短边长为6,则这个多边形的最长边为______ .
18
课堂小测
7、 如图所示的两个矩形相似吗?为什么?如果相似,相似比是多
少?
G
F
E
H
1.5
1
A
D
C
B
3
2
解:矩形ABCD相似于矩形EFGH,
因为它们的对应角相等,对应边成比例,
所以相似比为:
课堂小测
.
第二十七章
相似
九年级数学人教版·下册
27.1 图形的相似
第一课时
相似图形
教学目标
1.理解并掌握相似图形的概念及特征;(重点)
2.理解相似图形的特征,掌握识别相似图形的方法.(难点)
全等图形
指能够完全重合的两个图形,
即它们的形状和大小完全相同.
新课导入
新课导入
四阶魔方和三阶魔方形状相同吗?大小呢?
新课导入
问题1:图中的两个图形有什么关系?
它们还全等吗?
什么样的图形是全等图形?
形状相同,大小也相同.
不全等.形状相同,大小不相同.
全等.
新知探究
两个图形的形状完全相同 ,但图形的大小位置不一定相同,这样的图形叫做相似图形.
新知探究
新知探究
我们把形状相同的图形叫相似图形.
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
相似图形:
全等图形是相似图形,
相似图形不一定是全等图形.
新知探究
思考:如图是一个女孩从平面镜和哈哈镜里看到的自己的形象,这三个镜中的形象相似吗?
哈哈镜
平面镜
哈哈镜
(1)在平面镜中的像与物体的形状 ,大小 ,则从平面镜里看到的
自己的形象与女孩 相似图形(填“是”或“不是”).
(2)哈哈镜里看到的形象,有的被“压扁”了,有的被“拉长”了,所以哈哈镜中的
像与物体的形状 ,大小 ,则从哈哈镜里看到的自己的形象与
女孩 相似图形(填“是”或“不是”).
相同
相等
是
不同
不相等
不是
1.如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
相似
新知探究
新知探究
2.观察下面的图形(a)~(g),其中哪些是与(1)(2)或(3)相似的?
(a )与(1)、
(d)与(2)、
(g)与(3).
课堂小结
相似图形
两个图形的形状完全相同.
但图形的大小位置不一定相同.
课堂小测
1.下列四个命题:①所有的直角三角形都相似;②所有的等腰三角形都相似;
③所有的正方形都相似;④所有的菱形都相似.其中正确的有 ( )
A.2个 B.3个 C.4个 D.1个
D
2.下列图形是相似图形的是 ( )
A.①②③ B.②③④ C.①③④ D.①②④
A
课堂小测
3.下列图形不是相似图形的是 ( )
A.同一张底片冲洗出来的两张大小不同的照片
B.用放大镜将一个细小物体图案放大过程中原有图案和放大图案
C.某人的侧身照片和正面照片
D.大小不同的两张中国地图
C
课堂小测
4.想一想
(1)所有的圆都是相似图形吗?
(2)所有的等边三角形都是相似图形吗?
(3)所有的三角形都是相似图形吗?
(4)所有的正方形都是相似图形吗?
(5)所有的长方形都是相似图形吗?
是
是
不是
是
不是
第二课时
相似多边形
教学目标
1.理解并掌握相似多边形的概念及性质;(重点)
2.能利用成比例线段的概念及相似多边形的性质进行有关计算.(难点)
新课导入
将△ABC用2倍放大镜观察得到△A1B1C1,这两个三角形相似吗
这两个三角形中的对应角、对应边之间有什么关系
相似.
对应的角相等,对应的边成比例.
如图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形.
对于图中两个相似的四边形,它们的对应角,对应边的比是否相等?
相等
新知探究
新知探究
定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
相似比:相似多边形对应边的比叫做相似比,全等是相似比等于1的特殊情况.
符号语言(以四边形为例):
∵四边形ABCD∽四边形A′B′C′D′
(相似多边形的对应边成比例,对应角相等)
新知探究
例题 如图,四边形ABCD和EFGH相似,求∠α、∠ β的大小和EH的长度x.
24cm
x
解:
∵四边形ABCD和EFGH相似,
∴∠α=∠C=83 °,∠A=∠E=118 °.
118°
在四边形ABCD中
∠ β= 360°-( 78°+ 83°+ 118° )=81 °.
∵四边形ABCD和EFGH相似 ,
∴
,即
∴x=28(cm).
,
如图,矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所成的矩形EFGH和矩形ABCD是否相似
A
F
E
H
G
D
C
B
∴不相似
新知探究
新知探究
成比例线段:对于四条线段a,b,c,d,如果其中两条线段的比与另外两条线段的比相等,如 (即ad=bc),我们就说这四条线段成比例.
1.已知a,b,c,d是成比例线段,且a=3 cm,b=2 cm,c=6 cm,则d= cm.
2.在比例尺为1∶6000000的地图上,量得南京到北京的距离是15 cm,则这两地的实际距离是 km.
4
900
新知探究
课堂小结
相似多边形
定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
相似比:相似多边形对应边的比叫做相似比,全等是相似比等于1的特殊情况.
成比例线段:对于四条线段a,b,c,d,如果其中两条线段的比与另外两条线段的比相等,如 (即ad=bc),我们就说这四条线段成比例.
1、填空:
(1)等腰三角形两腰的比是________;
(2)直角三角形斜边上的中线和斜边的比是_________.
1∶1
1∶2
课堂小测
2、填空:
(1)如图①,则x= ,y = ,α= ;
(2)如图②,x= .
╯
80°
╰
65°
╯
80°
╮
125°
α
╭
3
6
x
y
图①
3
5
30
20
15
x
图②
2.5
1.5
90°
22.5
课堂小测
课堂小测
3、在两个相似的五边形中,一个五边形各边长分别为1,2,3,4,5,另
一个五边形最大边为10,则最短的边为( )
A. 2 B. 4 C. 6 D. 8
A
4、△ABC与△DEF相似,且相似比是 ,则△DEF与△ABC的相似比是( )
A. B. C. D.
B
5、 五边形ABCDE相似于五边形A′B′C′D′E′,它们的相似比为1 : 3.
(1)若∠D=135°,则∠D′= ______;
(2)若A′B′=15,则AB= ______.
135°
5
6、一个多边形的边长分别是2、3、4、5、6,另一个和它相似的 多边形的最短边长为6,则这个多边形的最长边为______ .
18
课堂小测
7、 如图所示的两个矩形相似吗?为什么?如果相似,相似比是多
少?
G
F
E
H
1.5
1
A
D
C
B
3
2
解:矩形ABCD相似于矩形EFGH,
因为它们的对应角相等,对应边成比例,
所以相似比为:
课堂小测
.
