初中数学人教版九年级下册27.1 图形的相似教案(共2课时)(含答案)
文档属性
| 名称 | 初中数学人教版九年级下册27.1 图形的相似教案(共2课时)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 285.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 17:23:51 | ||
图片预览


文档简介
27.1 图形的相似 教案(共2课时)
第1课时 相似图形
教学目标
1.通过具体实例认识相似图形,理解和掌握两个图形相似的概念.
2.掌握相似图形的识别方法.
3.通过观察、测量、辨析、归纳等数学活动,经历相似图形的概念的形成过程,培养学生观察能力及归纳总结能力.
教学重难点
重点:理解并掌握相似图形的概念及 特征.
难点:理解相似图形的特征,掌握识别相似图形的方法.
教学过程
情境导入
李明同学被评为五好学生,需向学校政教处上交四张相片.两张一寸的,贴在申报表上;一张两寸的,贴在证书上;一张五寸的,贴在学校光荣榜上.他去照相,要求照相的师傅给他照三种相片:一寸、两寸、五寸.照相师傅说,只照一次,有一张底片就可以了.你知道这是为什么吗?进入我们今天的学习吧,相信你一定会明白其中的道理.
探究新知
探究点一 相似图形
【例1】如图,下面四个选项中的图形与其相似的是( )
【解析】选项A是把原图拉长了,而选项D是把原图压扁了,因此它们与原图都不相似;选项B是正六边形,与原图的正五边形的边数不同,故选项B与原图也不相似;而选项C是将原图绕正五边形的中心旋转180°后,再按一定比例缩小得到的,因此选项C与原图相似.
【答案】C
【方法总结】判断两个图形的形状是否相同,应仔细观察,当两个图形的形状除了大小没有其他任何差异时,我们才可以说这两个图形相似.
探究点二 相似图形的特征
【例2】观察下列图形,哪些是相似 图形?
第一组:
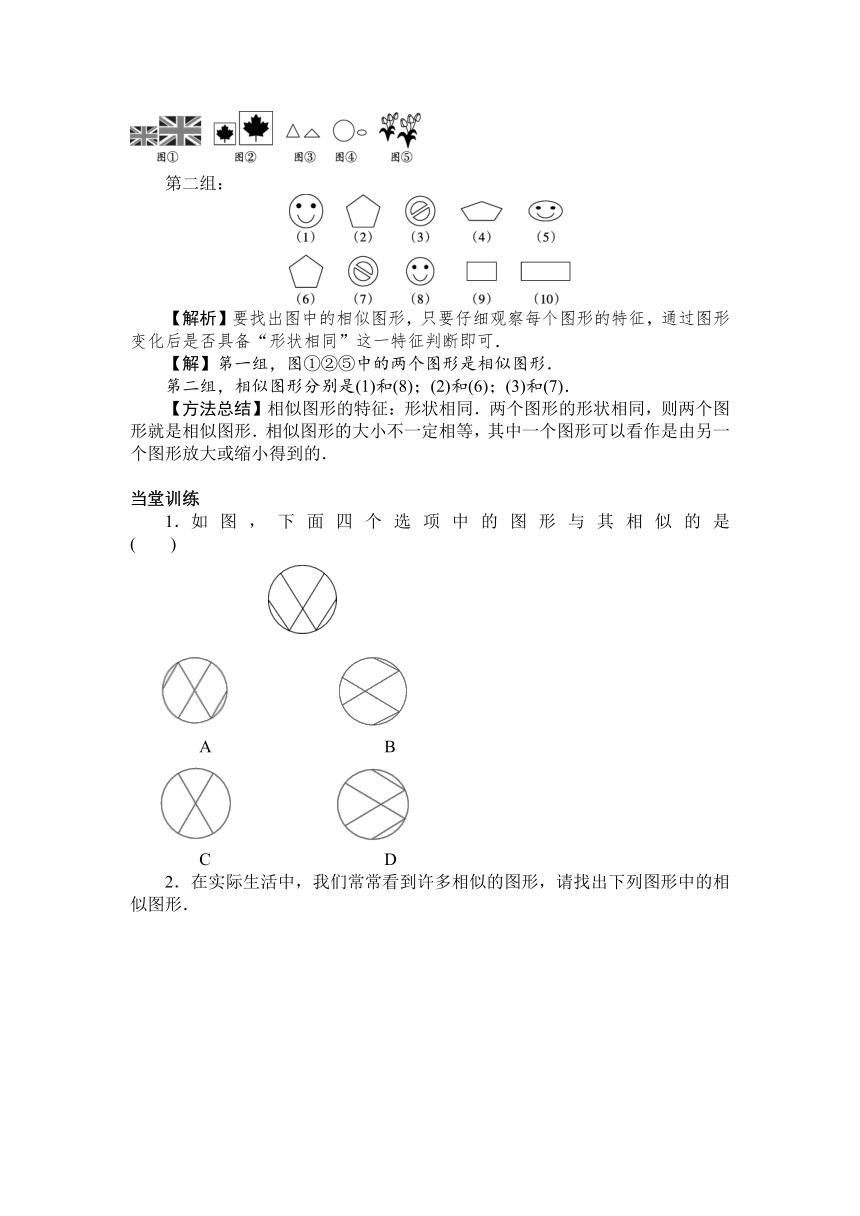
第二组:
【解析】要找出图中的相似图形,只要仔细观察每个图形的特征,通过图形变化后是否具备“形状相同”这一特征判断即可.
【解】第一组,图①②⑤中的两个图形是相似图形.
第二组,相似图形分别是(1)和(8);(2)和(6);(3)和(7).
【方法总结】相似图形的特征:形状相同.两个图形的形状相同,则两个图形就是相似图形.相似图形的大小不一定相等,其中一个图形可以看作是由另一个图形放大或缩小得到的.
当堂训练
如图,下面四个选项中的图形与其相似的是 ( )
A B
C D
2.在实际生活中,我们常常看到许多相似的图形,请找出下列图形中的相似图形.
答案
1.D
2.解:图①与图⑥、图②与图④、图③与图⑧、图⑤与图⑨分别是相似图形
板书设计
相似图形
1.认识相似图形
形状相同的图形叫做相似图形;全等图形是相似图形的一种特殊情况.
2.相似图形的特征
形状相同.相似图形只与形状有关,与图形的大小、位置无关.
课堂小结
本节课主要学习了相似图形的定义,明了了相似图形与全等图形之间的关系,掌握了相似图形的特征.
教学反思
本节课的重点是通过欣赏图形,观察图形的特征,归纳总结相似图形的概念和特征,并能总结全等图形与相似图形之间的关系.由于课时内容较少,学生易于掌握,在教学时用多媒体多展示一些相似图形的图片,可以用一些图形的不同角度和方向的图片,培养学生的观察能力.同时在课堂上注重培养学生自主学习的能力,教师起到引导作用即可,让学生多参与、思考、归纳,通过小组合作交流,达到掌握知识的目的.
第2课时 相似多边形
教学目标
1.了解成比例线段的概念,会判断已知线段是否成比例.
2.理解相似多边形的概念、性质及判定.
3.能根据相似多边形的有关概念和性质进行判断及有关计算.
4.通过应用成比例线段的定义及相似多边形的性质进行有关计算,体会方程思想在几何中的应用,渗透数形结合思想.
教学重难点
重点:理解并掌握相似多边形的概念及性质.
难点:探索相似多边形的性质中的“对应”关系.
教学过程
情境导入
如图是两个大小不同的正六边形螺母,左边的螺母可以看作是右边的螺母缩小得来的.由于不同的需求,螺母会有大小不同的各种型号,但其形状肯定是相同的.
日常生活中我们会碰到很多这种形状相同、大小不一定相同的图形.在数学上,我们把具有相同形状的图形称为相似图形.像这样的图形有哪些性质?下面我们就一起探讨一下吧!
探究新知
探究点一 成比例线段
【例1】已知线段a,b,c,d是成比例的线段,其中a=2 m,b=4 m,c=5 m,则d= ( )
A.1 m B.10 m
C. m D. m
【解析】∵线段a,b,c,d是成比例的线段,∴a∶b=c∶d,而a=2 m,b=4 m,c=5 m,∴d===10(m).
【答案】B
【方法总结】(1)在计算两条线段的比时要注意统一单位,此时两条线段的比与所采用的长度单位没有关系;(2)线段的比是一个没有单位的正数;(3)四条线段a,b,c,d成比例,记作=或a∶b=c∶d;(4)若四条线段满足=,则有ad=bc.
探究点二 相似多边形
类型一 利用相似多边形的性质求线段和角
【例2】如图所示,给出的两个四边形是相似图形(具体数据已标出),求出未知边a,b的长度及角α的值.
【解析】根据相似多边形对应角相等和对应边成比例解答.
【解】∵四边形ABCD与四边形A′B′C′D′相似,
∴∠B′=∠B=63°,∠D′=∠D,==,
即==,∴a=5,b=18.
在四边形A′B′C′D′中,
∠D′=360°-(84°+75°+63°)=138°,
∴α=∠D=∠D′=138°.
【方法总结】若两个多边形相似,那么它们的对应角相等,对应边成比例.在书写两个多边形相似时,要注意把表示对应角顶点的字母写在对应的位置上.
类型二 相似多边形的判定
【例3】一块长3 m、宽1.5 m的矩形黑板ABCD如图所示,镶在其外围的木质边框宽为75 cm.边框的内边缘所成的矩形ABCD与边框的外边缘所成的矩形EFGH相似吗?为什么?
【解析】两个矩形的四个角虽然相等,但四条边不一定对应成比例,判定两个矩形是否相似,关键是看对应边是否成比例.
【解】不相似.理由如下:
∵在矩形ABCD中,AB=1.5 m,AD=3 m,镶在其外围的木质边框宽为75 cm=0.75 m,
∴EF=1.5+2×0.75=3(m),EH=3+2×0.75=4.5(m),
∴==,==.
∵≠,
∴边框的内边缘所成的矩形ABCD与边框的外边缘所成的矩形EFGH不相似.
【方法总结】判定两个多边形相似,需要对应角相等,对应边成比例,这两个条件缺一不可.
课堂训练
1.若一张地图的比例尺是1∶150 000,在地图上量得甲、乙两地的距离是5 cm,则甲、乙两地的实际距离是 ( )
A.3 000 m B.3 500 m
C.5 000 m D.7 500 m
2.如图所示的两个多边形相似吗?说说你判断的理由.
答案
1.D 【解析】设甲、乙两地的实际距离是x cm.
根据题意,得1∶150 000=5∶x,解得x=750 000,750 000 cm=7 500 m.
2.解:不相似.理由如下:
∵∠D=360°-135°-95°-72°=58°,
∠G=360°-135°-72°-59°=94°,
∴两个四边形中不可能有“对应角相等”,
∴不相似.
板书设计
相似多边形
1.成比例线段的概念
(1)两条线段的长度比叫做这两条线段的比;
(2)对于四条线段a,b,c,d,如果其中两条线段的比与另外两条线段的比相等,如= (即ad=bc),我们就说这四条线段成比例;
(3)四条线段中有两条线段的比与另两条线段的比相等,就说这四条线段成比例.
2.相似多边形的定义和性质
(1)相似多边形定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
(2)相似多边形的性质:相似多边形的对应角相等,对应边成比例.
课堂总结
本节课主要学习了四条线段成比例,知道了相似多边形的定义和性质.
教学反思
本节课让学生经历“问题情境-建立模型-解释、应用与拓展”的过程.首先举出日常生活中常见的相似图形,让学生观察、思考得出相似图形的概念,体现了数学来源于生活这一本质特性.在此基础上,通过猜测、动手测量、动脑、自主探索、合作交流等方式,归纳出相似图形的性质以及图形相似的判定方法.让学生在自主探索、合作交流的过程中,体会到由特殊到一般的思想方法.
第1课时 相似图形
教学目标
1.通过具体实例认识相似图形,理解和掌握两个图形相似的概念.
2.掌握相似图形的识别方法.
3.通过观察、测量、辨析、归纳等数学活动,经历相似图形的概念的形成过程,培养学生观察能力及归纳总结能力.
教学重难点
重点:理解并掌握相似图形的概念及 特征.
难点:理解相似图形的特征,掌握识别相似图形的方法.
教学过程
情境导入
李明同学被评为五好学生,需向学校政教处上交四张相片.两张一寸的,贴在申报表上;一张两寸的,贴在证书上;一张五寸的,贴在学校光荣榜上.他去照相,要求照相的师傅给他照三种相片:一寸、两寸、五寸.照相师傅说,只照一次,有一张底片就可以了.你知道这是为什么吗?进入我们今天的学习吧,相信你一定会明白其中的道理.
探究新知
探究点一 相似图形
【例1】如图,下面四个选项中的图形与其相似的是( )
【解析】选项A是把原图拉长了,而选项D是把原图压扁了,因此它们与原图都不相似;选项B是正六边形,与原图的正五边形的边数不同,故选项B与原图也不相似;而选项C是将原图绕正五边形的中心旋转180°后,再按一定比例缩小得到的,因此选项C与原图相似.
【答案】C
【方法总结】判断两个图形的形状是否相同,应仔细观察,当两个图形的形状除了大小没有其他任何差异时,我们才可以说这两个图形相似.
探究点二 相似图形的特征
【例2】观察下列图形,哪些是相似 图形?
第一组:
第二组:
【解析】要找出图中的相似图形,只要仔细观察每个图形的特征,通过图形变化后是否具备“形状相同”这一特征判断即可.
【解】第一组,图①②⑤中的两个图形是相似图形.
第二组,相似图形分别是(1)和(8);(2)和(6);(3)和(7).
【方法总结】相似图形的特征:形状相同.两个图形的形状相同,则两个图形就是相似图形.相似图形的大小不一定相等,其中一个图形可以看作是由另一个图形放大或缩小得到的.
当堂训练
如图,下面四个选项中的图形与其相似的是 ( )
A B
C D
2.在实际生活中,我们常常看到许多相似的图形,请找出下列图形中的相似图形.
答案
1.D
2.解:图①与图⑥、图②与图④、图③与图⑧、图⑤与图⑨分别是相似图形
板书设计
相似图形
1.认识相似图形
形状相同的图形叫做相似图形;全等图形是相似图形的一种特殊情况.
2.相似图形的特征
形状相同.相似图形只与形状有关,与图形的大小、位置无关.
课堂小结
本节课主要学习了相似图形的定义,明了了相似图形与全等图形之间的关系,掌握了相似图形的特征.
教学反思
本节课的重点是通过欣赏图形,观察图形的特征,归纳总结相似图形的概念和特征,并能总结全等图形与相似图形之间的关系.由于课时内容较少,学生易于掌握,在教学时用多媒体多展示一些相似图形的图片,可以用一些图形的不同角度和方向的图片,培养学生的观察能力.同时在课堂上注重培养学生自主学习的能力,教师起到引导作用即可,让学生多参与、思考、归纳,通过小组合作交流,达到掌握知识的目的.
第2课时 相似多边形
教学目标
1.了解成比例线段的概念,会判断已知线段是否成比例.
2.理解相似多边形的概念、性质及判定.
3.能根据相似多边形的有关概念和性质进行判断及有关计算.
4.通过应用成比例线段的定义及相似多边形的性质进行有关计算,体会方程思想在几何中的应用,渗透数形结合思想.
教学重难点
重点:理解并掌握相似多边形的概念及性质.
难点:探索相似多边形的性质中的“对应”关系.
教学过程
情境导入
如图是两个大小不同的正六边形螺母,左边的螺母可以看作是右边的螺母缩小得来的.由于不同的需求,螺母会有大小不同的各种型号,但其形状肯定是相同的.
日常生活中我们会碰到很多这种形状相同、大小不一定相同的图形.在数学上,我们把具有相同形状的图形称为相似图形.像这样的图形有哪些性质?下面我们就一起探讨一下吧!
探究新知
探究点一 成比例线段
【例1】已知线段a,b,c,d是成比例的线段,其中a=2 m,b=4 m,c=5 m,则d= ( )
A.1 m B.10 m
C. m D. m
【解析】∵线段a,b,c,d是成比例的线段,∴a∶b=c∶d,而a=2 m,b=4 m,c=5 m,∴d===10(m).
【答案】B
【方法总结】(1)在计算两条线段的比时要注意统一单位,此时两条线段的比与所采用的长度单位没有关系;(2)线段的比是一个没有单位的正数;(3)四条线段a,b,c,d成比例,记作=或a∶b=c∶d;(4)若四条线段满足=,则有ad=bc.
探究点二 相似多边形
类型一 利用相似多边形的性质求线段和角
【例2】如图所示,给出的两个四边形是相似图形(具体数据已标出),求出未知边a,b的长度及角α的值.
【解析】根据相似多边形对应角相等和对应边成比例解答.
【解】∵四边形ABCD与四边形A′B′C′D′相似,
∴∠B′=∠B=63°,∠D′=∠D,==,
即==,∴a=5,b=18.
在四边形A′B′C′D′中,
∠D′=360°-(84°+75°+63°)=138°,
∴α=∠D=∠D′=138°.
【方法总结】若两个多边形相似,那么它们的对应角相等,对应边成比例.在书写两个多边形相似时,要注意把表示对应角顶点的字母写在对应的位置上.
类型二 相似多边形的判定
【例3】一块长3 m、宽1.5 m的矩形黑板ABCD如图所示,镶在其外围的木质边框宽为75 cm.边框的内边缘所成的矩形ABCD与边框的外边缘所成的矩形EFGH相似吗?为什么?
【解析】两个矩形的四个角虽然相等,但四条边不一定对应成比例,判定两个矩形是否相似,关键是看对应边是否成比例.
【解】不相似.理由如下:
∵在矩形ABCD中,AB=1.5 m,AD=3 m,镶在其外围的木质边框宽为75 cm=0.75 m,
∴EF=1.5+2×0.75=3(m),EH=3+2×0.75=4.5(m),
∴==,==.
∵≠,
∴边框的内边缘所成的矩形ABCD与边框的外边缘所成的矩形EFGH不相似.
【方法总结】判定两个多边形相似,需要对应角相等,对应边成比例,这两个条件缺一不可.
课堂训练
1.若一张地图的比例尺是1∶150 000,在地图上量得甲、乙两地的距离是5 cm,则甲、乙两地的实际距离是 ( )
A.3 000 m B.3 500 m
C.5 000 m D.7 500 m
2.如图所示的两个多边形相似吗?说说你判断的理由.
答案
1.D 【解析】设甲、乙两地的实际距离是x cm.
根据题意,得1∶150 000=5∶x,解得x=750 000,750 000 cm=7 500 m.
2.解:不相似.理由如下:
∵∠D=360°-135°-95°-72°=58°,
∠G=360°-135°-72°-59°=94°,
∴两个四边形中不可能有“对应角相等”,
∴不相似.
板书设计
相似多边形
1.成比例线段的概念
(1)两条线段的长度比叫做这两条线段的比;
(2)对于四条线段a,b,c,d,如果其中两条线段的比与另外两条线段的比相等,如= (即ad=bc),我们就说这四条线段成比例;
(3)四条线段中有两条线段的比与另两条线段的比相等,就说这四条线段成比例.
2.相似多边形的定义和性质
(1)相似多边形定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
(2)相似多边形的性质:相似多边形的对应角相等,对应边成比例.
课堂总结
本节课主要学习了四条线段成比例,知道了相似多边形的定义和性质.
教学反思
本节课让学生经历“问题情境-建立模型-解释、应用与拓展”的过程.首先举出日常生活中常见的相似图形,让学生观察、思考得出相似图形的概念,体现了数学来源于生活这一本质特性.在此基础上,通过猜测、动手测量、动脑、自主探索、合作交流等方式,归纳出相似图形的性质以及图形相似的判定方法.让学生在自主探索、合作交流的过程中,体会到由特殊到一般的思想方法.
