青岛版八年级数学下册第6章6.4三角形的中位线定理同步训练题(含答案)
文档属性
| 名称 | 青岛版八年级数学下册第6章6.4三角形的中位线定理同步训练题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 149.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-20 00:00:00 | ||
图片预览


文档简介
青岛版八年级数学下册第6章6.4三角形的中位线定理同步训练题(含答案)
一.选择题(共10小题)
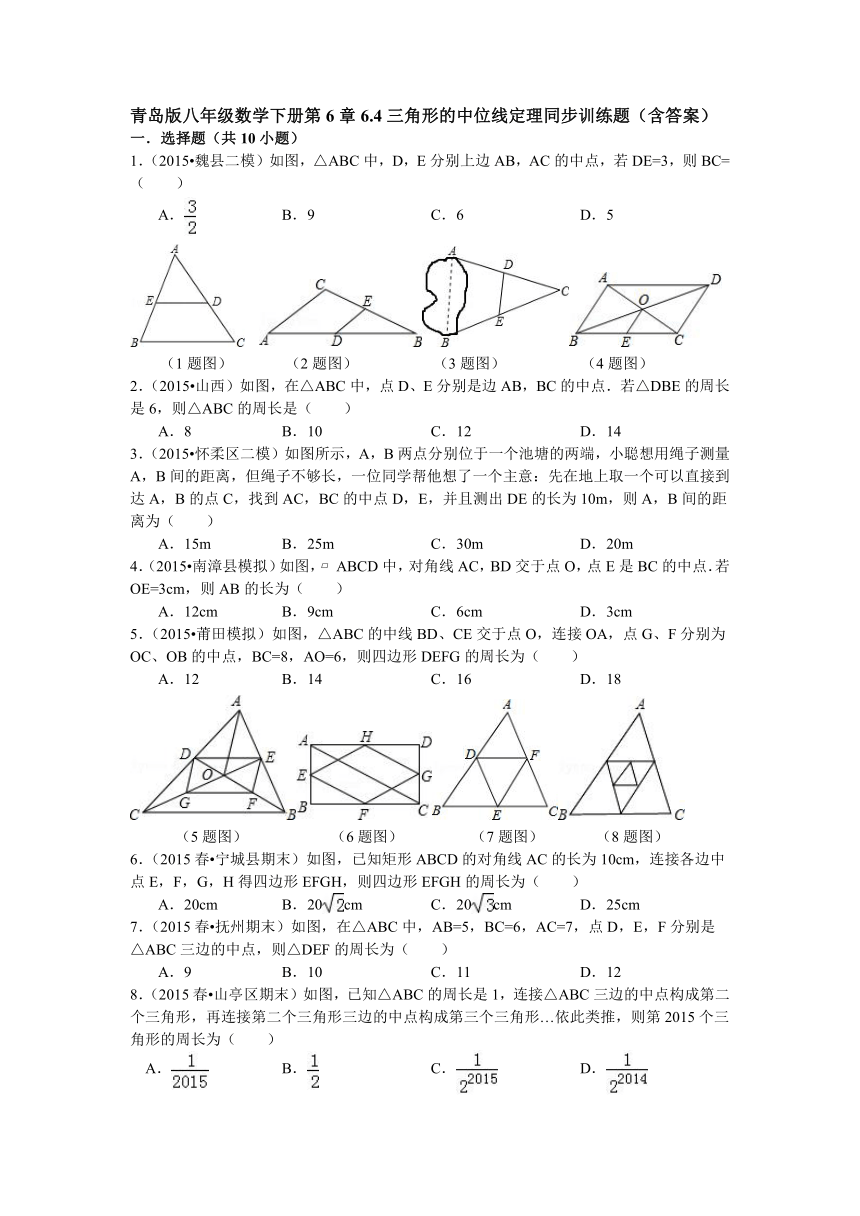
1.(2015 魏县二模)如图,△ABC中,D,E分别上边AB,AC的中点,若DE=3,则BC=( )
A. B. 9 C. 6 D. 5
(1题图) (2题图) (3题图) (4题图)
2.(2015 山西)如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A.8 B. 10 C. 12 D. 14
3.(2015 怀柔区二模)如图所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为10m,则A,B间的距离为( )
A.15m B. 25m C. 30m D. 20m
4.(2015 南漳县模拟)如图, ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
A.12cm B. 9cm C. 6cm D. 3cm
5.(2015 莆田模拟)如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=8,AO=6,则四边形DEFG的周长为( )
A.12 B. 14 C. 16 D. 18
(5题图) (6题图) (7题图) (8题图)
6.(2015春 宁城县期末)如图,已知矩形ABCD的对角线AC的长为10cm,连接各边中点E,F,G,H得四边形EFGH,则四边形EFGH的周长为( )
A.20cm B. 20cm C. 20cm D. 25cm
7.(2015春 抚州期末)如图,在△ABC中,AB=5,BC=6,AC=7,点D,E,F分别是△ABC三边的中点,则△DEF的周长为( )
A.9 B. 10 C. 11 D. 12
8.(2015春 山亭区期末)如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )
A. B. C. D.
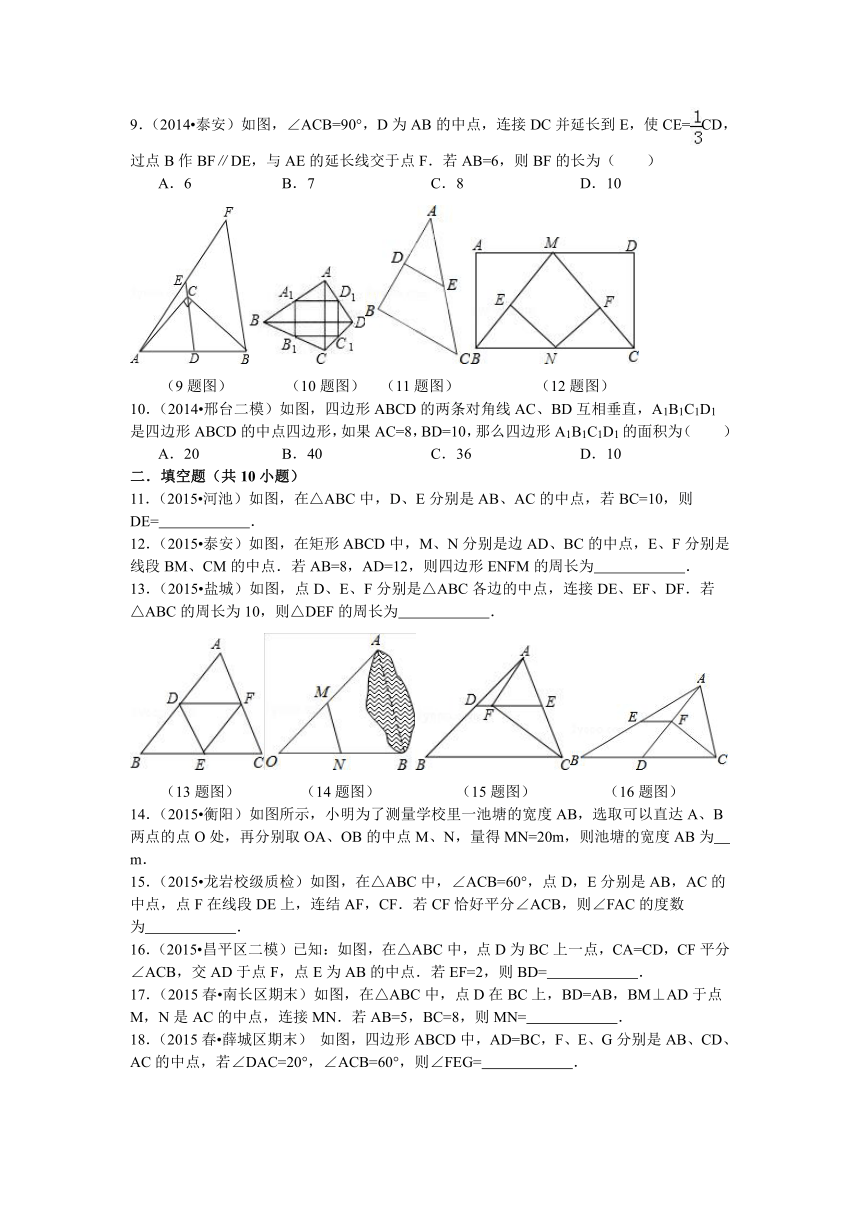
9.(2014 泰安)如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为( )
A.6 B. 7 C. 8 D. 10
(9题图) (10题图) (11题图) (12题图)
10.(2014 邢台二模)如图,四边形ABCD的两条对角线AC、BD互相垂直,A1B1C1D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面积为( )
A.20 B. 40 C. 36 D. 10
二.填空题(共10小题)
11.(2015 河池)如图,在△ABC中,D、E分别是AB、AC的中点,若BC=10,则DE= .
12.(2015 泰安)如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.若AB=8,AD=12,则四边形ENFM的周长为 .
13.(2015 盐城)如图,点D、E、F分别是△ABC各边的中点,连接DE、EF、DF.若△ABC的周长为10,则△DEF的周长为 .
(13题图) (14题图) (15题图) (16题图)
14.(2015 衡阳)如图所示,小明为了测量学校里一池塘的宽度AB,选取可以直达A、B两点的点O处,再分别取OA、OB的中点M、N,量得MN=20m,则池塘的宽度AB为 m.
15.(2015 龙岩校级质检)如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为 .
16.(2015 昌平区二模)已知:如图,在△ABC中,点D为BC上一点,CA=CD,CF平分∠ACB,交AD于点F,点E为AB的中点.若EF=2,则BD= .
17.(2015春 南长区期末)如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若AB=5,BC=8,则MN= .
18.(2015春 薛城区期末) 如图,四边形ABCD中,AD=BC,F、E、G分别是AB、CD、AC的中点,若∠DAC=20°,∠ACB=60°,则∠FEG= .
(17题图) (18题图) (19题图) (20题图)
19.(2015春 昌乐县期末)如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为 .
20.(2015春 胶州市期末)如图,△ABC中,D,E分别是AB,AC的中点,F是DE上一点,且AF⊥FC,若BC=9,DF=1,则AC的长为 .
三.解答题(共5小题)
21.(2014秋 龙口市期末)如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
求证:四边形DGFE是平行四边形.
22.(2015 邵阳)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
23.(2015春 临清市期中)已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高.求证:∠EDG=∠EFG.
24.(2015春 泗阳县期末)如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)试判断线段DE与FH之间的数量关系,并说明理由;
(2)求证:∠DHF=∠DEF.
25.(2015春 工业园区期中)如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.
青岛版八年级数学下册第6章6.4三角形的中位线定理同步训练题参考答案
一.选择题(共10小题)
1.C 2.C 3.D 4.C 5.B 6.A 7.A 8.D 9.C 10.A
二.填空题(共10小题)
11.5 12.20 13.5 14.40 15.60° 16.4 17. 18.20° 19.3 20.7
三.解答题(共5小题)
21.证明:∵D、E分别是AB、AC边的中点,
∴DE∥BC,且DE=BC,
同理,GF∥BC,且GF=BC,
∴DE∥GF且DE=GF,
四边形DGFE是平行四边形.
22.(1)证明:∵D、E分别为AB、AC的中点,∴DEBC,
∵延长BC至点F,使CF=BC,∴DEFC,即DE=CF;
(2)解:∵DEFC,∴四边形DEFC是平行四边形,∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴DC=EF=.
23.证明:连接EG,∵E、F、G分别是AB、BC、CA的中点,
∴EF为△ABC的中位线,EF=AC.(三角形的中位线等于第三边的一半)
又∵AD⊥BC,∴∠ADC=90°,DG为直角△ADC斜边上的中线,
∴DG=AC.(直角三角形斜边上的中线等于斜边的一半)
∴DG=EF.
同理DE=FG,EG=GE,
∴△EFG≌△GDE(SSS).
∴∠EDG=∠EFG.
(23题图) (24题图) (25题图)
24.解:(1)DE与FH相等.理由如下:∵D、E分别是AB、BC边的中点.
∴ED∥AC,DE=AC,
∵AH⊥BC,垂足为H,F是AC的中点,∴HF=AC,∴DE=FH.
(2)∵DH=AB,AD=AB,∴AD=DH,∴∠DAH=∠DHA,
同理可证:∠FAH=∠FHA,
∴∠DHF=∠DAF,
∵AD∥EF,DE∥AF,
∴四边形ADEF是平行四边形,
∴∠DEF=∠DAF,
∴∠DHF=∠DEF.
25.解:延长线段BN交AC于E.
∵AN平分∠BAC,
在△ABN和△AEN中,∴△ABN≌△AEN(SAS),
∴AE=AB=6,BN=NE,
又∵M是△ABC的边BC的中点,
∴CE=2MN=2×1.5=3,
∴△ABC的周长是AB+BC+AC=6+10+6+3=25.
一.选择题(共10小题)
1.(2015 魏县二模)如图,△ABC中,D,E分别上边AB,AC的中点,若DE=3,则BC=( )
A. B. 9 C. 6 D. 5
(1题图) (2题图) (3题图) (4题图)
2.(2015 山西)如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A.8 B. 10 C. 12 D. 14
3.(2015 怀柔区二模)如图所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为10m,则A,B间的距离为( )
A.15m B. 25m C. 30m D. 20m
4.(2015 南漳县模拟)如图, ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
A.12cm B. 9cm C. 6cm D. 3cm
5.(2015 莆田模拟)如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=8,AO=6,则四边形DEFG的周长为( )
A.12 B. 14 C. 16 D. 18
(5题图) (6题图) (7题图) (8题图)
6.(2015春 宁城县期末)如图,已知矩形ABCD的对角线AC的长为10cm,连接各边中点E,F,G,H得四边形EFGH,则四边形EFGH的周长为( )
A.20cm B. 20cm C. 20cm D. 25cm
7.(2015春 抚州期末)如图,在△ABC中,AB=5,BC=6,AC=7,点D,E,F分别是△ABC三边的中点,则△DEF的周长为( )
A.9 B. 10 C. 11 D. 12
8.(2015春 山亭区期末)如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )
A. B. C. D.
9.(2014 泰安)如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为( )
A.6 B. 7 C. 8 D. 10
(9题图) (10题图) (11题图) (12题图)
10.(2014 邢台二模)如图,四边形ABCD的两条对角线AC、BD互相垂直,A1B1C1D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面积为( )
A.20 B. 40 C. 36 D. 10
二.填空题(共10小题)
11.(2015 河池)如图,在△ABC中,D、E分别是AB、AC的中点,若BC=10,则DE= .
12.(2015 泰安)如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.若AB=8,AD=12,则四边形ENFM的周长为 .
13.(2015 盐城)如图,点D、E、F分别是△ABC各边的中点,连接DE、EF、DF.若△ABC的周长为10,则△DEF的周长为 .
(13题图) (14题图) (15题图) (16题图)
14.(2015 衡阳)如图所示,小明为了测量学校里一池塘的宽度AB,选取可以直达A、B两点的点O处,再分别取OA、OB的中点M、N,量得MN=20m,则池塘的宽度AB为 m.
15.(2015 龙岩校级质检)如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为 .
16.(2015 昌平区二模)已知:如图,在△ABC中,点D为BC上一点,CA=CD,CF平分∠ACB,交AD于点F,点E为AB的中点.若EF=2,则BD= .
17.(2015春 南长区期末)如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若AB=5,BC=8,则MN= .
18.(2015春 薛城区期末) 如图,四边形ABCD中,AD=BC,F、E、G分别是AB、CD、AC的中点,若∠DAC=20°,∠ACB=60°,则∠FEG= .
(17题图) (18题图) (19题图) (20题图)
19.(2015春 昌乐县期末)如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为 .
20.(2015春 胶州市期末)如图,△ABC中,D,E分别是AB,AC的中点,F是DE上一点,且AF⊥FC,若BC=9,DF=1,则AC的长为 .
三.解答题(共5小题)
21.(2014秋 龙口市期末)如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
求证:四边形DGFE是平行四边形.
22.(2015 邵阳)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
23.(2015春 临清市期中)已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高.求证:∠EDG=∠EFG.
24.(2015春 泗阳县期末)如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)试判断线段DE与FH之间的数量关系,并说明理由;
(2)求证:∠DHF=∠DEF.
25.(2015春 工业园区期中)如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.
青岛版八年级数学下册第6章6.4三角形的中位线定理同步训练题参考答案
一.选择题(共10小题)
1.C 2.C 3.D 4.C 5.B 6.A 7.A 8.D 9.C 10.A
二.填空题(共10小题)
11.5 12.20 13.5 14.40 15.60° 16.4 17. 18.20° 19.3 20.7
三.解答题(共5小题)
21.证明:∵D、E分别是AB、AC边的中点,
∴DE∥BC,且DE=BC,
同理,GF∥BC,且GF=BC,
∴DE∥GF且DE=GF,
四边形DGFE是平行四边形.
22.(1)证明:∵D、E分别为AB、AC的中点,∴DEBC,
∵延长BC至点F,使CF=BC,∴DEFC,即DE=CF;
(2)解:∵DEFC,∴四边形DEFC是平行四边形,∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴DC=EF=.
23.证明:连接EG,∵E、F、G分别是AB、BC、CA的中点,
∴EF为△ABC的中位线,EF=AC.(三角形的中位线等于第三边的一半)
又∵AD⊥BC,∴∠ADC=90°,DG为直角△ADC斜边上的中线,
∴DG=AC.(直角三角形斜边上的中线等于斜边的一半)
∴DG=EF.
同理DE=FG,EG=GE,
∴△EFG≌△GDE(SSS).
∴∠EDG=∠EFG.
(23题图) (24题图) (25题图)
24.解:(1)DE与FH相等.理由如下:∵D、E分别是AB、BC边的中点.
∴ED∥AC,DE=AC,
∵AH⊥BC,垂足为H,F是AC的中点,∴HF=AC,∴DE=FH.
(2)∵DH=AB,AD=AB,∴AD=DH,∴∠DAH=∠DHA,
同理可证:∠FAH=∠FHA,
∴∠DHF=∠DAF,
∵AD∥EF,DE∥AF,
∴四边形ADEF是平行四边形,
∴∠DEF=∠DAF,
∴∠DHF=∠DEF.
25.解:延长线段BN交AC于E.
∵AN平分∠BAC,
在△ABN和△AEN中,∴△ABN≌△AEN(SAS),
∴AE=AB=6,BN=NE,
又∵M是△ABC的边BC的中点,
∴CE=2MN=2×1.5=3,
∴△ABC的周长是AB+BC+AC=6+10+6+3=25.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
