青岛版八年级数学上册第5章5.5三角形内角和定理同步训练题(含答案)
文档属性
| 名称 | 青岛版八年级数学上册第5章5.5三角形内角和定理同步训练题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 144.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-20 00:00:00 | ||
图片预览


文档简介
青岛版八年级数学上册第5章5.5三角形内角和定理同步训练题(含答案)
一.选择题(共10小题)
1.(2015春 高密市期末)如图所示,被纸板遮住的三角形是( )
A.直角三角形 B. 锐角三角形
C.钝角三角形 D. 以上三种情况都有可能
(1题图) (3题图) (4题图) (5题图)
2.(2015 滨州)在△ABC中,∠A:∠B:∠C=3:4:5,则∠C等于( )
A.45° B. 60° C. 75° D. 90°
3.(2015 肥城市一模)将一副三角板按图中的方式叠放,则∠α等于( )
A.75° B. 60° C. 45° D. 30°
4.(2015 郑州模拟)如图,△ABC中,BO,CO分别是∠ABC,∠ACB的平分线,∠A=50°,则∠BOC等于( )
A.110° B. 115° C. 120° D. 130°
5.(2015 路南区一模)如果CD平分含30°三角板的∠ACB,则∠1等于( )
A.110° B. 105° C. 100° D. 95°
6.(2015 舟山模拟)如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠BDC等于( )
A.42° B. 66° C. 69° D. 77°
(6题图) (7题图) (10题图)
7.(2015 临夏州)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上的点,将△ABC沿着DE折叠压平,A与A′重合,若∠A=70°,则∠1+∠2=()
A.110° B. 140° C. 220° D. 70°
8.(2015春 普陀区期末)在△ABC中,如果∠A:∠B:∠C=1:1:2,那么△ABC的形状是( )
A.锐角三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形
9.(2015春 黄冈校级期末)直角三角形的两锐角平分线相交成的角的度数是( )
A.45° B. 135°
C.45°或135° D. 以上答案均不对
10.(2015春 沛县期末)如图,BI,CI分别平分∠ABC,∠ACB,若BAC=70°,则∠BIC=( )
A.140° B. 110° C. 125° D. 105°
二.填空题(共10小题)
11.(2015 鞍山一模)如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是 .
(11题图) (12题图) (13题图) (14题图)
12.(2015 黄冈校级模拟)如图,在△ABC中,∠B=42°,△ABC的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= .
13.(2015春 荔城区期末)如图,点O是△ABC的∠ABC与∠ACB两个角的角平分线的交点,若∠BOC=118°,则∠A的角度是 °.
14.(2015春 南安市期末)如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB、AC
上,将△ABC沿着DE折叠压平,使点A与点N重合.
(1)若∠B=35°,∠C=60°,则∠A的度数为 ;
(2)若∠A=70°,则∠1+∠2的度数为 .
15.(2015春 玉田县期末)如图,若CD平分∠ACE,BD平分∠ABC,∠A=45°,则∠D= °.
(15题图) (16题图) (17题图) (18题图)
16.(2015春 揭西县期末)如图,△ABC中,∠A=60°,∠B=70°,CD是∠ACB的平分线,点E在AC上,DE∥BC,则∠EDC的度数为 .
17.(2015春 道外区期末)如图,在△ABC中,∠B=30°,∠C=70°,AD平分∠BAC,交BC于F,DE⊥BC于E,则∠D= °.
18.(2015春 孟津县期末)如图,∠BDC=98°,∠ACD=38°,∠ABD=23°,则∠A的度数是 .
19.(2015春 南长区期中)一个正方形和两个等边三角形的位置如图所示,∠3=55°,则∠1+∠2= .
(19题图) (20题图)
20.(2015春 南长区期中)把一副常用的三角板如图所示拼在一起,点B在AE上,那么图中∠ABC= .
三.解答题(共4小题)
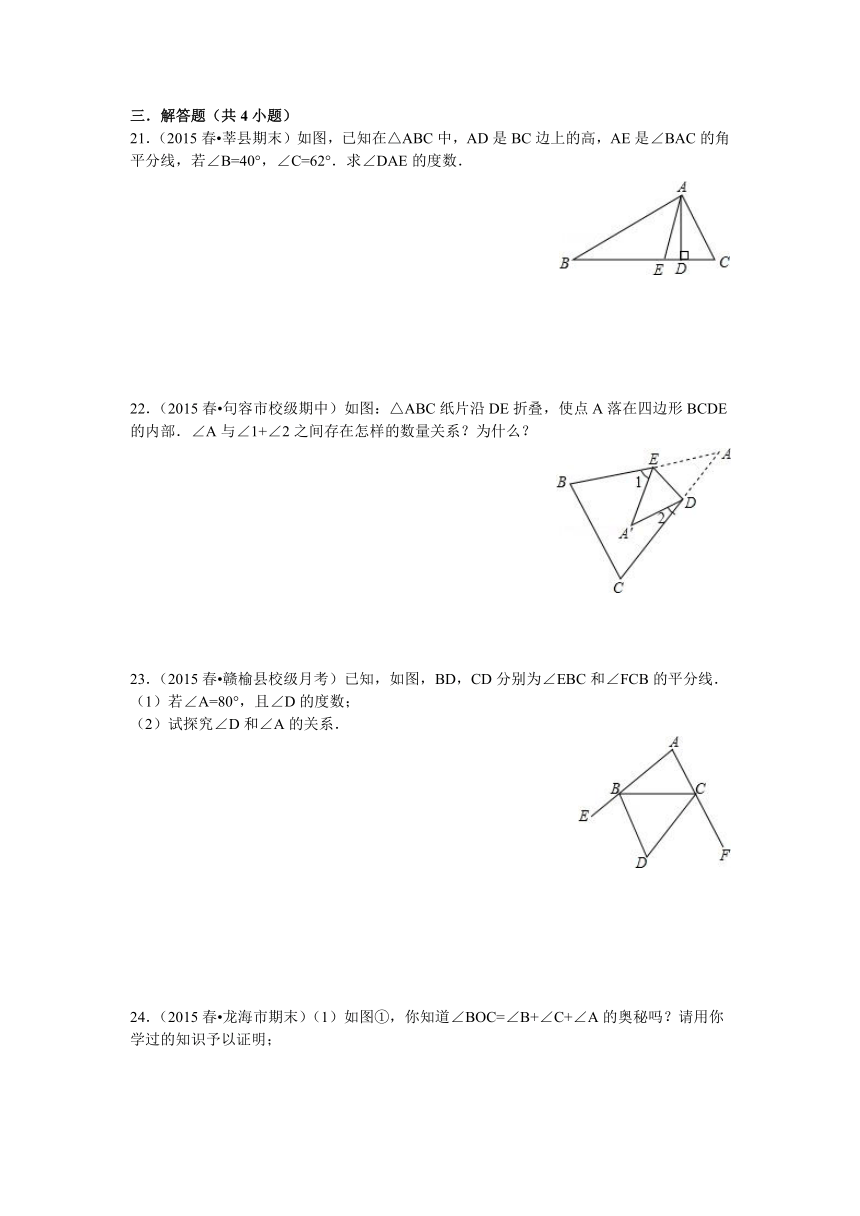
21.(2015春 莘县期末)如图,已知在△ABC中,AD是BC边上的高,AE是∠BAC的角平分线,若∠B=40°,∠C=62°.求∠DAE的度数.
22.(2015春 句容市校级期中)如图:△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部.∠A与∠1+∠2之间存在怎样的数量关系?为什么?
23.(2015春 赣榆县校级月考)已知,如图,BD,CD分别为∠EBC和∠FCB的平分线.
(1)若∠A=80°,且∠D的度数;
(2)试探究∠D和∠A的关系.
24.(2015春 龙海市期末)(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请用你学过的知识予以证明;
(2)如图②,设x=∠A+∠B+∠C+∠D+∠E,运用(1)中的结论填空.
x= °; x= °; x= °;
(3)如图③,一个六角星,其中∠BOD=70°,则:∠A+∠B+∠C+∠D+∠E+∠F= °.
青岛版八年级数学上册第5章5.5三角形内角和定理同步训练题参考答案
一.选择题(共10小题)
1.D 2.C 3.A 4.B 5.B 6.C 7.B 8.D 9.C 10.C
二.填空题(共10小题)
11.85° 12.69° 13.56 14.85°140° 15.22.5 16.25° 17.20
18.37° 19.95° 20.75°
三.解答题(共4小题)
21.解:∵∠B=40°,∠C=62°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°,
∴∠AED=∠B+∠BAE=40°+40°=80°,
∵AD⊥BC,
∴∠DAE=90°﹣∠AED=90°﹣80°=10°,
即∠DAE为10°.
22.解:2∠A=∠1+∠2,
理由:∵在四边形ADA′E中,∠A+∠A′+∠ADA′+∠AEA′=360°,
则2∠A+180°﹣∠2+180°﹣∠1=360°,
∴可得2∠A=∠1+∠2.
23.解:(1)∵BD、CD分别是∠EBC和∠FCB的平分线,
∴∠CBD=∠CBE,∠BCD=∠BCF,
∴∠CBD+∠BCD=∠CBE+∠BCF=(∠CBE+∠BCF)=(∠A+∠ACB+∠A+∠ABC)
=(180°+∠A),
∴∠D=180°﹣(∠CBD+∠BCD)=180°﹣(180°+∠A)=90°﹣∠A=90°﹣×80°=50°.
(2)∵BD、CD分别是∠EBC和∠FCB的平分线,
∴∠CBD=∠CBE,∠BCD=∠BCF,
∴∠CBD+∠BCD
=∠CBE+∠BCF
=(∠CBE+∠BCF)
=(∠A+∠ACB+∠A+∠ABC)
=(180°+∠A),
∴∠D=180°﹣(∠CBD+∠BCD)
=180°﹣(180°+∠A)
=90°﹣∠A.
24.解:(1)如图①,延长BO交AC于点D,
∠BOC=∠BDC+∠C,
又∵∠BDC=∠A+∠B,
∴∠BOC=∠B+∠C+∠A.
(2)如图②,,
根据外角的性质,可得
∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图③,,
根据外角的性质,可得
∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图④,延长EA交CD于点F,EA和BC交于点G,,
根据外角的性质,可得
∠GFC=∠D+∠E,∠FGC=∠A+∠B,
∵∠GFC+∠FGC+∠C=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
(3)如图⑤,,
∵∠BOD=70°,
∴∠A+∠C+∠E=70°,
∴∠B+∠D+∠F=70°,
∴∠A+∠B+∠C+∠D+∠E+∠F=70°+70°=140°.
故答案为:180、180、180、140.
一.选择题(共10小题)
1.(2015春 高密市期末)如图所示,被纸板遮住的三角形是( )
A.直角三角形 B. 锐角三角形
C.钝角三角形 D. 以上三种情况都有可能
(1题图) (3题图) (4题图) (5题图)
2.(2015 滨州)在△ABC中,∠A:∠B:∠C=3:4:5,则∠C等于( )
A.45° B. 60° C. 75° D. 90°
3.(2015 肥城市一模)将一副三角板按图中的方式叠放,则∠α等于( )
A.75° B. 60° C. 45° D. 30°
4.(2015 郑州模拟)如图,△ABC中,BO,CO分别是∠ABC,∠ACB的平分线,∠A=50°,则∠BOC等于( )
A.110° B. 115° C. 120° D. 130°
5.(2015 路南区一模)如果CD平分含30°三角板的∠ACB,则∠1等于( )
A.110° B. 105° C. 100° D. 95°
6.(2015 舟山模拟)如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠BDC等于( )
A.42° B. 66° C. 69° D. 77°
(6题图) (7题图) (10题图)
7.(2015 临夏州)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上的点,将△ABC沿着DE折叠压平,A与A′重合,若∠A=70°,则∠1+∠2=()
A.110° B. 140° C. 220° D. 70°
8.(2015春 普陀区期末)在△ABC中,如果∠A:∠B:∠C=1:1:2,那么△ABC的形状是( )
A.锐角三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形
9.(2015春 黄冈校级期末)直角三角形的两锐角平分线相交成的角的度数是( )
A.45° B. 135°
C.45°或135° D. 以上答案均不对
10.(2015春 沛县期末)如图,BI,CI分别平分∠ABC,∠ACB,若BAC=70°,则∠BIC=( )
A.140° B. 110° C. 125° D. 105°
二.填空题(共10小题)
11.(2015 鞍山一模)如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是 .
(11题图) (12题图) (13题图) (14题图)
12.(2015 黄冈校级模拟)如图,在△ABC中,∠B=42°,△ABC的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= .
13.(2015春 荔城区期末)如图,点O是△ABC的∠ABC与∠ACB两个角的角平分线的交点,若∠BOC=118°,则∠A的角度是 °.
14.(2015春 南安市期末)如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB、AC
上,将△ABC沿着DE折叠压平,使点A与点N重合.
(1)若∠B=35°,∠C=60°,则∠A的度数为 ;
(2)若∠A=70°,则∠1+∠2的度数为 .
15.(2015春 玉田县期末)如图,若CD平分∠ACE,BD平分∠ABC,∠A=45°,则∠D= °.
(15题图) (16题图) (17题图) (18题图)
16.(2015春 揭西县期末)如图,△ABC中,∠A=60°,∠B=70°,CD是∠ACB的平分线,点E在AC上,DE∥BC,则∠EDC的度数为 .
17.(2015春 道外区期末)如图,在△ABC中,∠B=30°,∠C=70°,AD平分∠BAC,交BC于F,DE⊥BC于E,则∠D= °.
18.(2015春 孟津县期末)如图,∠BDC=98°,∠ACD=38°,∠ABD=23°,则∠A的度数是 .
19.(2015春 南长区期中)一个正方形和两个等边三角形的位置如图所示,∠3=55°,则∠1+∠2= .
(19题图) (20题图)
20.(2015春 南长区期中)把一副常用的三角板如图所示拼在一起,点B在AE上,那么图中∠ABC= .
三.解答题(共4小题)
21.(2015春 莘县期末)如图,已知在△ABC中,AD是BC边上的高,AE是∠BAC的角平分线,若∠B=40°,∠C=62°.求∠DAE的度数.
22.(2015春 句容市校级期中)如图:△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部.∠A与∠1+∠2之间存在怎样的数量关系?为什么?
23.(2015春 赣榆县校级月考)已知,如图,BD,CD分别为∠EBC和∠FCB的平分线.
(1)若∠A=80°,且∠D的度数;
(2)试探究∠D和∠A的关系.
24.(2015春 龙海市期末)(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请用你学过的知识予以证明;
(2)如图②,设x=∠A+∠B+∠C+∠D+∠E,运用(1)中的结论填空.
x= °; x= °; x= °;
(3)如图③,一个六角星,其中∠BOD=70°,则:∠A+∠B+∠C+∠D+∠E+∠F= °.
青岛版八年级数学上册第5章5.5三角形内角和定理同步训练题参考答案
一.选择题(共10小题)
1.D 2.C 3.A 4.B 5.B 6.C 7.B 8.D 9.C 10.C
二.填空题(共10小题)
11.85° 12.69° 13.56 14.85°140° 15.22.5 16.25° 17.20
18.37° 19.95° 20.75°
三.解答题(共4小题)
21.解:∵∠B=40°,∠C=62°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°,
∴∠AED=∠B+∠BAE=40°+40°=80°,
∵AD⊥BC,
∴∠DAE=90°﹣∠AED=90°﹣80°=10°,
即∠DAE为10°.
22.解:2∠A=∠1+∠2,
理由:∵在四边形ADA′E中,∠A+∠A′+∠ADA′+∠AEA′=360°,
则2∠A+180°﹣∠2+180°﹣∠1=360°,
∴可得2∠A=∠1+∠2.
23.解:(1)∵BD、CD分别是∠EBC和∠FCB的平分线,
∴∠CBD=∠CBE,∠BCD=∠BCF,
∴∠CBD+∠BCD=∠CBE+∠BCF=(∠CBE+∠BCF)=(∠A+∠ACB+∠A+∠ABC)
=(180°+∠A),
∴∠D=180°﹣(∠CBD+∠BCD)=180°﹣(180°+∠A)=90°﹣∠A=90°﹣×80°=50°.
(2)∵BD、CD分别是∠EBC和∠FCB的平分线,
∴∠CBD=∠CBE,∠BCD=∠BCF,
∴∠CBD+∠BCD
=∠CBE+∠BCF
=(∠CBE+∠BCF)
=(∠A+∠ACB+∠A+∠ABC)
=(180°+∠A),
∴∠D=180°﹣(∠CBD+∠BCD)
=180°﹣(180°+∠A)
=90°﹣∠A.
24.解:(1)如图①,延长BO交AC于点D,
∠BOC=∠BDC+∠C,
又∵∠BDC=∠A+∠B,
∴∠BOC=∠B+∠C+∠A.
(2)如图②,,
根据外角的性质,可得
∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图③,,
根据外角的性质,可得
∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图④,延长EA交CD于点F,EA和BC交于点G,,
根据外角的性质,可得
∠GFC=∠D+∠E,∠FGC=∠A+∠B,
∵∠GFC+∠FGC+∠C=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
(3)如图⑤,,
∵∠BOD=70°,
∴∠A+∠C+∠E=70°,
∴∠B+∠D+∠F=70°,
∴∠A+∠B+∠C+∠D+∠E+∠F=70°+70°=140°.
故答案为:180、180、180、140.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
