青岛版八年级数学上册第2章2.2轴对称的基本性质同步训练题(含答案)
文档属性
| 名称 | 青岛版八年级数学上册第2章2.2轴对称的基本性质同步训练题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 120.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-20 00:00:00 | ||
图片预览


文档简介
青岛版八年级数学上册第2章2.2轴对称的基本性质同步训练题(含答案)
一.选择题(共10小题)
1.(2015 河南模拟)正方形ABCD边长为a,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图,则图中阴影部分的面积之和等于( )
A.a2 B. 0.25a2 C. 0.5a2 D. 2
(1题图) (2题图) (3题图) (9题图)
2.(2015 温州一模)如图,若 ABCD与 BCFE关于BC所在直线对称,∠ABE=86°,则∠E等于( )
A.137° B. 104° C. 94° D. 86°
3.(2015春 泾阳县期末)如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB∥DF B. ∠B=∠E
C.AB=DE D. AD的连线被MN垂直平分
4.(2015春 龙海市期末)下列说法中不正确的是( )
A. 线段有1条对称轴 B. 等边三角形有3条对称轴
C. 角只有1条对称轴 D. 底与腰不相等的等腰三角形只有一条对称轴
5.(2015春 潜江校级期中)下列图形中对称轴最多的是( )
A.等腰三角形 B. 正方形 C. 圆形 D. 线段
6.(2015 金溪县模拟)点M(﹣2,1)关于x轴的对称点N的坐标是( )
A.(2,1) B. (﹣2,1) C. (﹣2,﹣1) D. (2,﹣1)
7.(2015 邯郸二模)在平面直角坐标系中,点P(﹣2,3)关于y轴的对称点的坐标( )
A.(﹣2,﹣3) B. (2,﹣3) C. (﹣2,3) D. (2,3)
8.(2015 唐山三模)在平面直角坐标系中,已知点A(m,3)与点B(4,n)关于y轴对称,那么(m+n)2015的值为( )
A.﹣1 B. 1 C. ﹣72015 D. 72015
9.(2015 黄岛区校级模拟)如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(﹣1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是( ) A.(3,1) B. (﹣3,﹣1) C. (1,﹣3) D. (3,﹣1)
10.(2015 内江)如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
A. B. 2 C. 2 D.
二.填空题(共10小题)
11.(2015 常州模拟)如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB为 .
12.(2015 眉山)点P(3,2)关于y轴对称的点的坐标是 .
13.(2015 滨州模拟)在平面直角坐标系中,点M(﹣3,2)关于x轴对称的点的坐标是 .
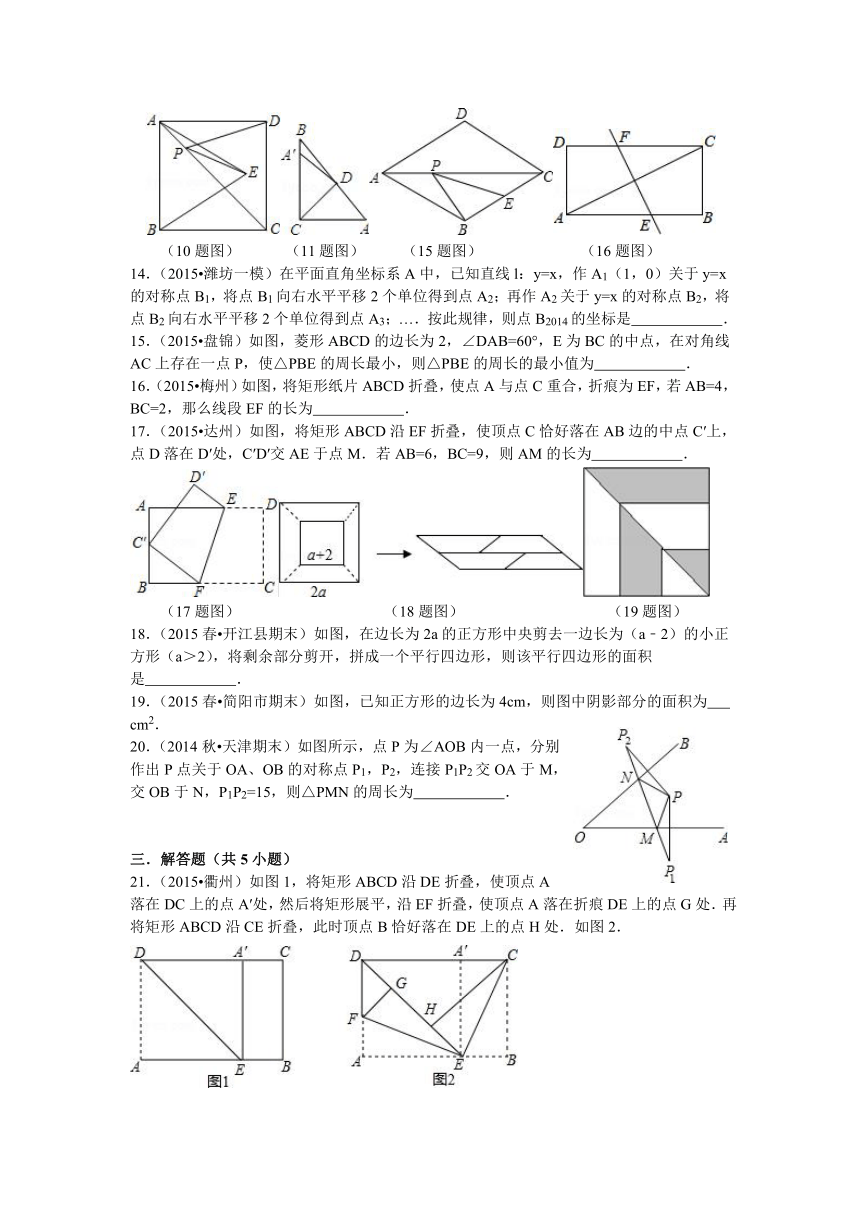
(10题图) (11题图) (15题图) (16题图)
14.(2015 潍坊一模)在平面直角坐标系A中,已知直线l:y=x,作A1(1,0)关于y=x的对称点B1,将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2,将点B2向右水平平移2个单位得到点A3;….按此规律,则点B2014的坐标是 .
15.(2015 盘锦)如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为 .
16.(2015 梅州)如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为 .
17.(2015 达州)如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,点D落在D′处,C′D′交AE于点M.若AB=6,BC=9,则AM的长为 .
(17题图) (18题图) (19题图)
18.(2015春 开江县期末)如图,在边长为2a的正方形中央剪去一边长为(a﹣2)的小正方形(a>2),将剩余部分剪开,拼成一个平行四边形,则该平行四边形的面积是 .
19.(2015春 简阳市期末)如图,已知正方形的边长为4cm,则图中阴影部分的面积为 cm2.
20.(2014秋 天津期末)如图所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 .
三.解答题(共5小题)
21.(2015 衢州)如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.
(1)求证:EG=CH;
(2)已知AF=,求AD和AB的长.
22.(2015 贺州)如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.
(1)求证:AF=EF;
(2)求证:BF平分∠ABD.
23.(2015春 启东市校级月考)如图,点P在∠AOB内,M、N分别是点P关于AO、BO的对称点,MN分别交AO,BO于点E、F,若△PEF的周长等于20cm,求MN的长.
24.(2014秋 广州校级期末)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后△ABC的顶点均在格点上.
(1)写出点A、B、C的坐标;
(2)写出△ABC关于x轴对称的△A1B1C1的顶点A1、B1、C1的坐标;
(3)求S△ABC.
25.(2015 乐山)如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
青岛版八年级数学上册第2章2.2轴对称的基本性质同步训练题参考答案
一.选择题(共10小题)
1.C 2.A 3.A 4.A 5.C 6.C 7.D 8.A 9.A 10.B
二.填空题(共10小题)
11.10° 12.(-3,2) 13.(-3,-2) 14.(2013,2014) 15.+1
16. 17. 18.3a2+4a-4 19.8 20.15
三.解答题(共5小题)
21.(1)证明:由折叠知AE=AD=EG,BC=CH,
∵四边形ABCD是矩形,∴AD=BC,∴EG=CH;
(2)解:∵∠ADE=45°,∠FGE=∠A=90°,AF=,∴DG=,DF=2,
∴AD=AF+DF=+2;
由折叠知∠AEF=∠GEF,∠BEC=∠HEC,∴∠GEF+∠HEC=90°,∠AEF+∠BEC=90°,
∵∠AEF+∠AFE=90°,∴∠BEC=∠AFE,
在△AEF与△BCE中,,∴△AEF≌△BCE(AAS),∴AF=BE,
∴AB=AE+BE=+2+=2+2.
22.(1)证明:在矩形ABCD中,AB=CD,∠A=∠C=90°,
∵△BED是△BCD翻折而成,∴ED=CD,∠E=∠C,∴ED=AB,∠E=∠A.
在△ABF与△EDF中,∵,∴△ABF≌△EDF(AAS),∴AF=EF;
(2)在Rt△BCD中,∵DC=DE=4,DB=8,∴sin∠CBD==,
∴∠CBD=30°,
∴∠EBD=∠CBD=30°,
∴∠ABF=90°﹣30°×2=30°,
∴∠ABF=∠DBF,
∴BF平分∠ABD.
23.解:∵M、N分别是点P关于AO、BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长等于20cm,
∴MN=20cm.
24.解:(1)A(1,3),B(﹣1,2),C(2,0);
(2)A1(1,﹣3),B1(﹣1,﹣2),C1(2,0);
(3)S△ABC=3×3﹣×2×3﹣×1×3﹣×2×1=.
25. 解:(1)∵AD∥BC,∴∠ADB=∠DBC,
根据折叠的性质∠ADB=∠BDF,∠F=∠A=∠C=90°,
∴∠DBC=∠BDF,
∴BE=DE,
在△DCE和△BFE中,,∴△DCE≌△BFE;
(2)在Rt△BCD中,
∵CD=2,∠ADB=∠DBC=30°,
∴BC=2,
在Rt△BCD中,
∵CD=2,∠EDC=30°,
∴DE=2EC,
∴(2EC)2﹣EC2=CD2,
∴CE=,
∴BE=BC﹣EC=.
一.选择题(共10小题)
1.(2015 河南模拟)正方形ABCD边长为a,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图,则图中阴影部分的面积之和等于( )
A.a2 B. 0.25a2 C. 0.5a2 D. 2
(1题图) (2题图) (3题图) (9题图)
2.(2015 温州一模)如图,若 ABCD与 BCFE关于BC所在直线对称,∠ABE=86°,则∠E等于( )
A.137° B. 104° C. 94° D. 86°
3.(2015春 泾阳县期末)如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB∥DF B. ∠B=∠E
C.AB=DE D. AD的连线被MN垂直平分
4.(2015春 龙海市期末)下列说法中不正确的是( )
A. 线段有1条对称轴 B. 等边三角形有3条对称轴
C. 角只有1条对称轴 D. 底与腰不相等的等腰三角形只有一条对称轴
5.(2015春 潜江校级期中)下列图形中对称轴最多的是( )
A.等腰三角形 B. 正方形 C. 圆形 D. 线段
6.(2015 金溪县模拟)点M(﹣2,1)关于x轴的对称点N的坐标是( )
A.(2,1) B. (﹣2,1) C. (﹣2,﹣1) D. (2,﹣1)
7.(2015 邯郸二模)在平面直角坐标系中,点P(﹣2,3)关于y轴的对称点的坐标( )
A.(﹣2,﹣3) B. (2,﹣3) C. (﹣2,3) D. (2,3)
8.(2015 唐山三模)在平面直角坐标系中,已知点A(m,3)与点B(4,n)关于y轴对称,那么(m+n)2015的值为( )
A.﹣1 B. 1 C. ﹣72015 D. 72015
9.(2015 黄岛区校级模拟)如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(﹣1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是( ) A.(3,1) B. (﹣3,﹣1) C. (1,﹣3) D. (3,﹣1)
10.(2015 内江)如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
A. B. 2 C. 2 D.
二.填空题(共10小题)
11.(2015 常州模拟)如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB为 .
12.(2015 眉山)点P(3,2)关于y轴对称的点的坐标是 .
13.(2015 滨州模拟)在平面直角坐标系中,点M(﹣3,2)关于x轴对称的点的坐标是 .
(10题图) (11题图) (15题图) (16题图)
14.(2015 潍坊一模)在平面直角坐标系A中,已知直线l:y=x,作A1(1,0)关于y=x的对称点B1,将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2,将点B2向右水平平移2个单位得到点A3;….按此规律,则点B2014的坐标是 .
15.(2015 盘锦)如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为 .
16.(2015 梅州)如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为 .
17.(2015 达州)如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,点D落在D′处,C′D′交AE于点M.若AB=6,BC=9,则AM的长为 .
(17题图) (18题图) (19题图)
18.(2015春 开江县期末)如图,在边长为2a的正方形中央剪去一边长为(a﹣2)的小正方形(a>2),将剩余部分剪开,拼成一个平行四边形,则该平行四边形的面积是 .
19.(2015春 简阳市期末)如图,已知正方形的边长为4cm,则图中阴影部分的面积为 cm2.
20.(2014秋 天津期末)如图所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 .
三.解答题(共5小题)
21.(2015 衢州)如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.
(1)求证:EG=CH;
(2)已知AF=,求AD和AB的长.
22.(2015 贺州)如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.
(1)求证:AF=EF;
(2)求证:BF平分∠ABD.
23.(2015春 启东市校级月考)如图,点P在∠AOB内,M、N分别是点P关于AO、BO的对称点,MN分别交AO,BO于点E、F,若△PEF的周长等于20cm,求MN的长.
24.(2014秋 广州校级期末)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后△ABC的顶点均在格点上.
(1)写出点A、B、C的坐标;
(2)写出△ABC关于x轴对称的△A1B1C1的顶点A1、B1、C1的坐标;
(3)求S△ABC.
25.(2015 乐山)如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
青岛版八年级数学上册第2章2.2轴对称的基本性质同步训练题参考答案
一.选择题(共10小题)
1.C 2.A 3.A 4.A 5.C 6.C 7.D 8.A 9.A 10.B
二.填空题(共10小题)
11.10° 12.(-3,2) 13.(-3,-2) 14.(2013,2014) 15.+1
16. 17. 18.3a2+4a-4 19.8 20.15
三.解答题(共5小题)
21.(1)证明:由折叠知AE=AD=EG,BC=CH,
∵四边形ABCD是矩形,∴AD=BC,∴EG=CH;
(2)解:∵∠ADE=45°,∠FGE=∠A=90°,AF=,∴DG=,DF=2,
∴AD=AF+DF=+2;
由折叠知∠AEF=∠GEF,∠BEC=∠HEC,∴∠GEF+∠HEC=90°,∠AEF+∠BEC=90°,
∵∠AEF+∠AFE=90°,∴∠BEC=∠AFE,
在△AEF与△BCE中,,∴△AEF≌△BCE(AAS),∴AF=BE,
∴AB=AE+BE=+2+=2+2.
22.(1)证明:在矩形ABCD中,AB=CD,∠A=∠C=90°,
∵△BED是△BCD翻折而成,∴ED=CD,∠E=∠C,∴ED=AB,∠E=∠A.
在△ABF与△EDF中,∵,∴△ABF≌△EDF(AAS),∴AF=EF;
(2)在Rt△BCD中,∵DC=DE=4,DB=8,∴sin∠CBD==,
∴∠CBD=30°,
∴∠EBD=∠CBD=30°,
∴∠ABF=90°﹣30°×2=30°,
∴∠ABF=∠DBF,
∴BF平分∠ABD.
23.解:∵M、N分别是点P关于AO、BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长等于20cm,
∴MN=20cm.
24.解:(1)A(1,3),B(﹣1,2),C(2,0);
(2)A1(1,﹣3),B1(﹣1,﹣2),C1(2,0);
(3)S△ABC=3×3﹣×2×3﹣×1×3﹣×2×1=.
25. 解:(1)∵AD∥BC,∴∠ADB=∠DBC,
根据折叠的性质∠ADB=∠BDF,∠F=∠A=∠C=90°,
∴∠DBC=∠BDF,
∴BE=DE,
在△DCE和△BFE中,,∴△DCE≌△BFE;
(2)在Rt△BCD中,
∵CD=2,∠ADB=∠DBC=30°,
∴BC=2,
在Rt△BCD中,
∵CD=2,∠EDC=30°,
∴DE=2EC,
∴(2EC)2﹣EC2=CD2,
∴CE=,
∴BE=BC﹣EC=.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
