第二单元认识三角形和四边形(讲义)-2023-2024学年四年级下册数学北师大版(含解析)
文档属性
| 名称 | 第二单元认识三角形和四边形(讲义)-2023-2024学年四年级下册数学北师大版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 276.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 13:08:18 | ||
图片预览




文档简介
第二单元认识三角形和四边形(知识精讲+典题精练)
2023-2024学年四年级下册数学重难点单元培优讲义
(北师大版)
1.立体图形的分类及识别
【知识点归纳】
1.立体几何图形:
从实物中抽象出来的各种图形,统称为几何图形,几何图形是数学研究的主要对象之一.有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是立体图形.由一个或多个面围成的可以存在于现实生活中的三维图形.点动成线,线动成面,面动成体.即由面围成体,看一个体最多看到立体图形实物三个面.
2.常见立体几何图形及性质:
(1)正方体:
有8个顶点,6个面.每个面面积相等(或每个面都有正方形组成).有12条棱,每条棱长的长度都相等.(正方体是特殊的长方体)
(2)长方体:
有8个顶点,6个面.每个面都由长方形或相对的一组正方形组成.有12条棱,相对的4条棱的棱长相等.
(3)圆柱:
上下两个面为大小相同的圆形.有一个曲面叫侧面.展开后为长方形或正方形或平行四边形.有无数条高,这些高的长度都相等.
(4)圆锥:
有1个顶点,1个曲面,一个底面.展开后为扇形.只有1条高.四面体有1个顶点,四面六条棱高.
(5)直三棱柱:
三条侧棱切平行,上表面和下表面是平行且全等的三角形.
(6)球:
球是生活中最常见的图形之一,例如篮球、足球都是球,球是由一个面所围成的几何体.
2.平面图形的分类及识别
【知识点归纳】
1.概念:有些几何图形(如线段、角、三角形、长方形、圆等)的各个部分都在同一平面内,它们是平面图形.
2.平面图形分类:
(1)三角形:按边分有等腰三角形,不等腰三角形.按角分有:锐角三角形.直角三角形,钝角三角形.
(2)四边形:任意四边形,平行四边形,梯形.
(3)圆形:扇形.
3.正方形的特征及性质
【知识点归纳】
1.概念:有一组邻边相等且一个角是直角的平行四边形叫做正方形.
2.性质:
(1)边:两组对边分别平行;四条边都相等;相邻边互相垂直
(2)内角:四个角都是90°;
(3)对角线:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角;
(4)对称性:既是中心对称图形,又是轴对称图形(有四条对称轴).
(5)正方形具有平行四边形、菱形、矩形的一切性质.
(6)特殊性质:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
(7)正方形是特殊的长方形.
4.四边形的特点、分类及识别
【知识点归纳】
1.四边形的特点:四边形就是四条线段围成的图形,有四条边,四个角,且内角和是360°.
2.四边形的分类:
任意四边形:图形没有平行的边
平行四边形:图形两组平行的边
梯形:图形只有一组平行的边
3.四边形的识别:
根据分类特地进行识别即可.
5.三角形的分类
【知识点归纳】
1.按角分
判定法一:
锐角三角形:三个角都小于90°.
直角三角形:可记作Rt△.其中一个角必须等于90°.
钝角三角形:有一个角大于90°.
判定法二:
锐角三角形:最大角小于90°.
直角三角形:最大角等于90°.
钝角三角形:最大角大于90°.
其中锐角三角形和钝角三角形统称为斜三角形.
2.按边分
不等边三角形;
等腰三角形;
等边三角形.
6.三角形的内角和
【知识点归纳】
三角形内角和为180°.
直角三角形的两个锐角互余.
7.三角形边的关系
【知识点归纳】
1、两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
2、三角形任意两边的和大于第三边。
8.平行四边形的特征及性质
【知识点归纳】
平行四边形的概念:
1.两组对边分别平行的四边形叫做平行四边形.
平行四边形用符号“ ABCD”,如平行四边形ABCD记作“ ABCD”.
(1)平行四边形属于平面图形.
(2)平行四边形属于四边形.
(3)平行四边形中还包括特殊的平行四边形:矩形,正方形和菱形等.
(4)平行四边形属于中心对称图形.
2.平行四边形的性质:
主要性质
(矩形、菱形、正方形都是特殊的平行四边形.)
(1)如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等.
(简述为“平行四边形的两组对边分别相等”)
(2)如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等.
(简述为“平行四边形的两组对角分别相等”)
(3)夹在两条平行线间的平行线段相等.
(4)平行四边形的面积等于底和高的积.(可视为矩形)
(5)过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形.
(6)平行四边形是中心对称图形,对称中心是两对角线的交点.
(7)平行四边形不是轴对称图形,矩形和菱形是轴对称图形.
注:正方形,矩形以及菱形也是一种特殊的平行四边形,三者具有平行四边形的性质.
9.梯形的特征及分类
【知识点归纳】
1.概念:梯形是指一组对边平行而另一组对边不平行的四边形.
2.分类:
(1)直角梯形:有一个角为直角的梯形为直角梯形
(2)等腰梯形:两腰相等的梯形叫做等腰梯形
(3)一般梯形.
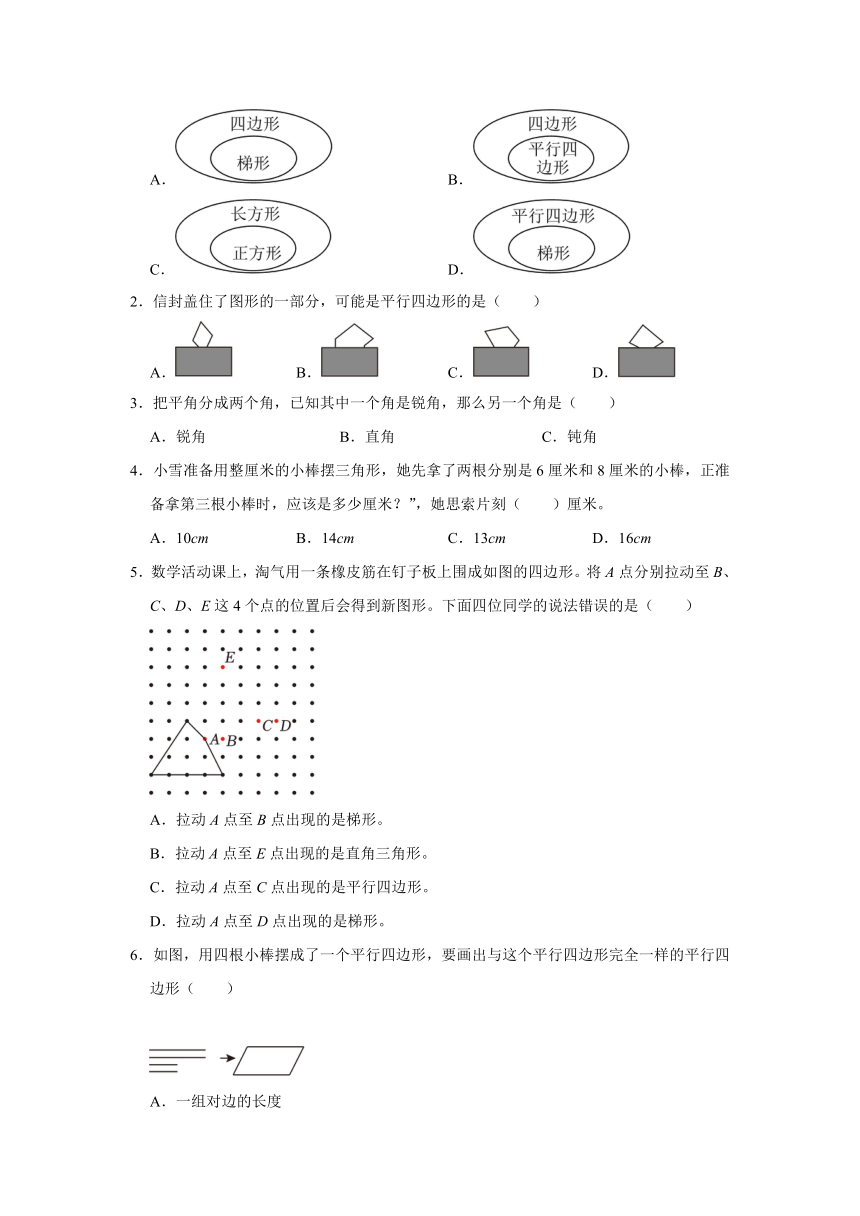
一.选择题(共7小题)
1.这学期我们又认识了很多平面图形,它们之间有着密切的联系。下面选项中,表示它们之间关系错误的是( )
A. B.
C. D.
2.信封盖住了图形的一部分,可能是平行四边形的是( )
A. B. C. D.
3.把平角分成两个角,已知其中一个角是锐角,那么另一个角是( )
A.锐角 B.直角 C.钝角
4.小雪准备用整厘米的小棒摆三角形,她先拿了两根分别是6厘米和8厘米的小棒,正准备拿第三根小棒时,应该是多少厘米?”,她思索片刻( )厘米。
A.10cm B.14cm C.13cm D.16cm
5.数学活动课上,淘气用一条橡皮筋在钉子板上围成如图的四边形。将A点分别拉动至B、C、D、E这4个点的位置后会得到新图形。下面四位同学的说法错误的是( )
A.拉动A点至B点出现的是梯形。
B.拉动A点至E点出现的是直角三角形。
C.拉动A点至C点出现的是平行四边形。
D.拉动A点至D点出现的是梯形。
6.如图,用四根小棒摆成了一个平行四边形,要画出与这个平行四边形完全一样的平行四边形( )
A.一组对边的长度
B.相邻两条边的长度
C.相邻两条边的长度和它们之间夹角的大小
D.四条边的长度
7.用四根木条钉成一个长方形,用手拉动一组对边,使它变成一个平行四边形( )
A.周长不变,面积也不变
B.周长变大,面积也变大
C.周长变小,面积也变小
D.周长不变,面积变小
二.填空题(共6小题)
8.
有 个,
有 个,
有 个,
有 个。
9.任意一个三角形,最多有 个锐角,最少有 个锐角;任意一个三角形,最多有 个钝角,最少有 个钝角。
10.通过研究发现当梯形的上底和下底 时就成了平行四边形,当梯形的上底 时就成了三角形。
11.下面是7根小棒的长度,用来围四边形。
上面的①~⑦根小棒,能围成平行四边形的4根小棒是 ;能围成等腰梯形的4根小棒是 。(填序号)
12.梯形有 组对边互相平行,平行四边形有 组对边互相平行。平行四边形具有 的特性,请写出一个生活中利用这一特性的事例: 。
13.在直角三角形中,其中一个锐角是a°,另一个锐角是 。
三.判断题(共7小题)
14.四边形的对边相等.
15.一个梯形上底与下底间的距离处处相等.
16.钝角三角形的内角和等于锐角三角形的内角和。
17.正方形的两组对边分别平行.
18.平行四边形有无数条高,所有的高都相等.
19.4个角都是直角的四边形一定是正方形.
20.长方形与正方形都是四边形。
四.计算题(共1小题)
21.求出下面三角形中未知角的度数.
五.应用题(共8小题)
22.王师傅用一根70厘米长的木条做了一个平行四边形框架,其中一条边的长是20厘米,另一条边长是多少厘米?
23.向阳小学要举行一次风筝比赛。设计要求这个风筝的造型是等腰三角形,它的一个底角是42°,计算一下这个风筝的顶角是多少度?
24.兰兰不小心打碎了一块三角形的玻璃,现在要配一个完全一样的玻璃,那么兰兰只需要带其中哪一块就可以?
25.一个三角形中,∠A的度数是27.5°,∠B的度数是∠A的1.6倍
26.一个等腰三角的一个顶角是64°,它的一个底角是多少度?如果它的底角是64°,那么它的顶角是多少度?
27.一个等腰三角形的其中一个内角是76°,这个等腰三角形的另外两个内角分别是多少度?
28.曲米有两根同样长的小棒,长5dm,如果她想用3根小棒摆成一个三角形(取整分米数)?曲婷给了她一根小棒,结果摆成的三角形一个底角是35°。顶角是多少度?
29.小嘉有一个等腰三角形的风筝,它的一个底角是75°,它的顶角是多少度?
第二单元认识三角形和四边形(知识精讲+典题精练)-2023-2024学年四年级下册(北师大版)
参考答案与试题解析
一.选择题(共7小题)
1.【答案】D
【分析】根据平行四边形的对边平行且相等,梯形只有一组对边平行,所以平行四边形不包含梯形,据此解答即可。
【解答】解:分析可知,它们之间关系错误的是。
故选:D。
【点评】本题考查了平行四边形和梯形的特征,结合题意分析解答即可。
2.【答案】A
【分析】两组对边分别平行的四边形叫做平行四边形,据此解答。
【解答】解:信封盖住了图形的一部分,可能是平行四边形的是。
故选:A。
【点评】本题考查了平行四边形的特征。
3.【答案】C
【分析】根据锐角、直角、钝角、平角的意义,小于90度的角叫做锐角;等于90度的角叫做直角;等于90度小于180度的角叫做钝角,等于180度的角叫做平角.据此解答即可.
【解答】解:由分析可知:平角=锐角+钝角,
答:把平角分成两个角,已知其中一个角是锐角.
故选:C.
【点评】此题考查的目的是理解掌握锐角、直角、钝角、平角的意义.
4.【答案】C
【分析】根据三角形两边之和大于第三边,两边之差小于第三边,解答此题即可。
【解答】解:8厘米﹣6厘米=4厘米
8厘米+6厘米=14厘米
4厘米<第三边<14厘米
答:她拿的第三根小棒长度是13厘米。
故选:C。
【点评】熟练掌握三角形的三边关系,是解答此题的关键。
5.【答案】A
【分析】梯形是指一组对边平行而另一组对边不平行的四边形,两组对边分别平行的四边形叫做平行四边形,有一个角是直角的三角形是直角三角形,据此解答即可。
【解答】解:A. 拉动A点至B点出现的不是梯形,所以本选项说法错误。
B. 拉动A点至E点出现的是直角三角形,所以本选项说法正确。
C. 拉动A点至C点出现的是平行四边形,所以本选项说法正确。
D. 拉动A点至D点出现的是梯形,所以本选项说法正确。
故选:A。
【点评】本题考查了梯形、直角三角形、平行四边形的特征和认识,结合题意分析解答即可。
6.【答案】C
【分析】根据平行四边形的对边平行且相等,用四根小棒摆成了一个平行四边形,要画出与这个平行四边形完全一样的平行四边形,需要知道这个平行四边形相邻两条边的长度和它们之间夹角的大小,据此解答即可。
【解答】解:用四根小棒摆成了一个平行四边形,要画出与这个平行四边形完全一样的平行四边形。
故选:C。
【点评】本题考查了平行四边形的特征和画法,结合题意分析解答即可。
7.【答案】D
【分析】根据长方形和平行四边形的特征和性质可知,把一个长方形框架拉成一个平行四边形,四条边的长度不变,只是高变小了;所以根据周长的求法,可知周长不变;根据面积的求法,可知面积变小了;据此解答。
【解答】解:把一个长方形拉成一个平行四边形,四条边的长度不变;所以周长不变。
故选:D。
【点评】解决此题的关键是弄清:把一个长方形拉成一个平行四边形,四条边的长度不变,只是高变小了。
二.填空题(共6小题)
8.【答案】3;3;3;4。
【分析】根据正方体、长方体、圆柱、球的特征进行分类识别,再数出相应的数量即可。
【解答】解:有3个,
有3个,
有3个,
有4个。
故答案为:3;4;3;4。
【点评】本题考查了正方体、长方体、圆柱、球的特征,从而进行分类识别。
9.【答案】3;2;1;0。
【分析】根据三角形的内角和是180度,锐角:大于0°,小于90°的角;钝角:大于90°,小于180°的角;进行解答即可。
【解答】解:任意一个三角形,最多有3个锐角;任意一个三角形,最少有0个钝角。
故答案为:5;2;1;8。
【点评】此题考查了三角形的内角和及钝角、锐角的概念,结合题意分析解答即可。
10.【答案】相等,为0。
【分析】如图:
由图可知:当梯形的上底逐渐缩小到一点时,梯形就转化成三角形;当梯形的上底增大到与下底相等时,梯形就转化成平行四边形,据此解答即可。
【解答】解:研究发现当梯形的上底和下底相等时就成了平行四边形,当梯形的上底为0时就成了三角形。
故答案为:相等,为0。
【点评】本题考查了三角形、梯形和平行四边形的特征,解答此题的关键是通过画图,进行分析,继而得出结论。
11.【答案】①②③④; ③④⑤⑥。(答案不唯一)
【分析】平行四边形的对边平行且相等,等腰梯形的两条腰相等,且上下底互相平行,据此解答。
【解答】解:上面的①~⑦根小棒,能围成平行四边形的4根小棒是①②③④。
故答案为:①②③④; ③④⑤⑥
【点评】本题考查了平行四边形及等腰梯形的特征。
12.【答案】一,两,易变形,平行四边形伸缩门(答案不唯一)。
【分析】根据平行四边形、梯形的特征,可得平行四边形的两组对边互相平行,并且相等,梯形只有一组对边互相平行;
平行四边形具有易变形的特性,生活中的平行四边形伸缩门就利用这个特性制作,据此解答。
【解答】解:梯形有一组对边互相平行,平行四边形有两组对边互相平行,生活中的平行四边形伸缩门就利用这个特性制作
故答案为:一,两,易变形。
【点评】此题主要考查了平行四边形、梯形的特征和应用,要熟练掌握,解答此题的关键是要明确:平行四边形的两组对边互相平行,并且相等,梯形只有一组对边互相平行,平行四边形具有易变形的特性。
13.【答案】(90﹣a)°。
【分析】根据三角形的内角和是180度可知,直角三角形中两个锐角的和是90度;用90度减去其中一个锐角的度数,就是另一个锐角的度数。
【解答】解:在一个直角三角形中,其中一个锐角是a度。
故答案为:(90﹣a)°。
【点评】本题考查了三角形的内角和,掌握三角形的内角和以及用含字母的式子表示数量关系是解题的关键。
三.判断题(共7小题)
14.【答案】×
【分析】在同一平面内,由不在同一直线上四条线段依次首尾相接围成的封闭的图形叫做四边形,由此即可判断.
【解答】解:由分析可知,四边形的对边不一定相等;
故答案为:×.
【点评】此题主要考查四边形与正方形的定义.
15.【答案】见试题解答内容
【分析】因为梯形的上下底是平行的,所以夹在两平行线之间的距离是处处相等,据此可知:梯形上底与下底间的距离处处相等的说法是正确的.
【解答】解:梯形上底与下底间的距离就是这个梯形的高,所以处处相等的说法是正确的.
故判断为:√.
【点评】此题考查梯形的特征,即上下底平行,还要明确夹在两平行线之间的距离是处处相等的.
16.【答案】√
【分析】根据任何三角形内角和都是180°即可解决。
【解答】解:因为任何三角形内角和都是180°,所以原题说法是正确的。
故答案为:√。
【点评】此题考查了三角形的内角和是180°。
17.【答案】√
【分析】四条边都相等的是正方形;也就是说:正方形的两组对边分别平行,它是特殊的平行四边形;由此解答即可.
【解答】解:正方形的两组对边分别平行,说法正确;
故答案为:√.
【点评】此题应根据正方形的特征进行解答.
18.【答案】见试题解答内容
【分析】根据平行四边行的定义可知,有两组对边平行的四边行叫平行四边形,平行四边形的高为两组边的距离,所以平行四边形有两组高,每组的高都相等且有无数条.
【解答】解:根据平行四边行的定义可知,有两组对边平行的四边行叫平行四边形,所以平行四边形有两组高;
所以上面的说法是错误的.
故答案为:×.
【点评】此题考查了平行四边形高的有关知识.
19.【答案】×
【分析】根据正方形的特征及性质可知:具有四条边都相等且四个角都是直角的四边形为正方形,据此判断即可.
【解答】解:因为四边相等,四个角都角是直角的四边形是正方形,
所以题干的说法不全面,四个角都是直角的四边形还可能是长方形,
因此题干的说法是错误的;
故答案为:×.
【点评】本题主要考查正方形的特征及性质.
20.【答案】√
【分析】四边形就是四条线段围成的图形,有四条边,四个角。
【解答】解:长方形与正方形都是四边形。原题说法正确。
故答案为:√。
【点评】本题考查了四边形的特征。
四.计算题(共1小题)
21.【答案】见试题解答内容
【分析】根据三角形的内角和是180°,用180°减去已知的2个角的度数,就是要求的角的度数,列式解答即可.
【解答】解:∠1=180°﹣70°﹣38°
=110°﹣38°
=72°
答:∠1等于72度.
180°﹣120°﹣30°
=60°﹣30°
=30°
答:第三个角等于30度.
∠6=180°﹣90°﹣30°
=90°﹣30°
=60°
答:∠1等于60度.
180°﹣90°﹣60°
=90°﹣60°
=30°
答:第三个角等于30度.
【点评】本题考查的是三角形的内角和的运用,注意直角等于90°,三角形的内角和等于180°.
五.应用题(共8小题)
22.【答案】见试题解答内容
【分析】70厘米即围成平行四边形的周长,根据平行四边形特征:两组对边分别相等,所以平行四边形的周长等于两条相邻边的和乘2,即可解答.
【解答】解:70÷2﹣20
=35﹣20
=15(厘米)
答:另一条边长是15厘米.
【点评】此题应结合题意,并根据平行四边形的特点进行分析、解答.
23.【答案】96度。
【分析】根据三角形的内角和等于180°和等腰三角形的两个底角相等,解答此题即可。
【解答】解:180°﹣42°×2
=180°﹣84°
=96°
答:这个风筝的顶角是96度。
【点评】熟练掌握三角形的内角和定理,是解答此题的关键。
24.【答案】见试题解答内容
【分析】根据三角形的内角和定理,可由两个已知角算出第三个内角的度数,而只有第三块玻璃含有2个内角,据此解答即可.
【解答】解:兰兰不小心打碎了一块三角形的玻璃,现在要配一个完全一样的玻璃.
答:兰兰只需要带第3块就可以.
【点评】解答此题的关键是明确第3块玻璃不仅含有2个内角还含有三角形的一条完整的边,这样配出的三角形玻璃就与原来的玻璃完全一样.
25.【答案】见试题解答内容
【分析】根据题意,先利用“求一个数的几倍是多少,用乘法计算”,求∠B的度数;然后利用三角形内角和定理:三角形的内角和是180°,求∠C的度数,进而判断三角形的形状.
【解答】解:∠B=27.5°×1.6=44°
∠C=180°﹣(27.5°+44°)=108.5°
108.8°>90°
答:∠C=108.5°,这是一个钝角三角形.
【点评】本题主要考查三角形的内角和,关键利用三角形内角和定理做题.
26.【答案】58°;52°。
【分析】三角形内角和等于180°,等腰三角形的两个底角相等;180°减顶角的度数,再除以2等于一个底角的度数;180°减两个底角的度数,等于顶角的度数;据此即可解答。
【解答】解:(180°﹣64°)÷2
=116°÷2
=58°
180°﹣64°×5
=180°﹣128°
=52°
答:一个等腰三角的一个顶角是64°,它的一个底角是58°,它的顶角是52°。
【点评】本题主要考查学生对三角形的内角和及等腰三角形的特征的掌握和灵活运用。
27.【答案】52°、52°或76°、28°。
【分析】根据三角形的内角和是180°,当76°是顶角时,用180°减去76°,再除以2,求出底角的度数;当76°是底角时,用三角形的内角和减去两个76°就是顶角的度数。
【解答】解:(180°﹣76°)÷2
=104°÷2
=52°
180°﹣76°×4
=180°﹣152°
=28°
答:这个等腰三角形的另外两个内角是52°、52°或76°。
【点评】熟练掌握三角形的内角和以及等腰三角形的特征是解题的关键。
28.【答案】9分米;110度。
【分析】根据三角形任意两边之和大于第三边,和三角形的内角和等于180°,解答此题即可。
【解答】解:第3根小棒<5+2
第三根小棒<10(分米)
答:第3根小棒最长是9分米。
180°﹣35°×5
=180°﹣70°
=110°
答:顶角是110度。
【点评】熟练掌握三角形的三边关系和三角形内角和定理,是解答此题的关键。
29.【答案】30 度。
【分析】根据三角形的内角和等于180°和等腰三角形的两个底角相等,解答此题即可。
【解答】解:180﹣2×75
=180﹣150
=30(度)
答:它的顶角是 30 度。
【点评】熟练掌握三角形的内角和,是解答此题的关键。
2023-2024学年四年级下册数学重难点单元培优讲义
(北师大版)
1.立体图形的分类及识别
【知识点归纳】
1.立体几何图形:
从实物中抽象出来的各种图形,统称为几何图形,几何图形是数学研究的主要对象之一.有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是立体图形.由一个或多个面围成的可以存在于现实生活中的三维图形.点动成线,线动成面,面动成体.即由面围成体,看一个体最多看到立体图形实物三个面.
2.常见立体几何图形及性质:
(1)正方体:
有8个顶点,6个面.每个面面积相等(或每个面都有正方形组成).有12条棱,每条棱长的长度都相等.(正方体是特殊的长方体)
(2)长方体:
有8个顶点,6个面.每个面都由长方形或相对的一组正方形组成.有12条棱,相对的4条棱的棱长相等.
(3)圆柱:
上下两个面为大小相同的圆形.有一个曲面叫侧面.展开后为长方形或正方形或平行四边形.有无数条高,这些高的长度都相等.
(4)圆锥:
有1个顶点,1个曲面,一个底面.展开后为扇形.只有1条高.四面体有1个顶点,四面六条棱高.
(5)直三棱柱:
三条侧棱切平行,上表面和下表面是平行且全等的三角形.
(6)球:
球是生活中最常见的图形之一,例如篮球、足球都是球,球是由一个面所围成的几何体.
2.平面图形的分类及识别
【知识点归纳】
1.概念:有些几何图形(如线段、角、三角形、长方形、圆等)的各个部分都在同一平面内,它们是平面图形.
2.平面图形分类:
(1)三角形:按边分有等腰三角形,不等腰三角形.按角分有:锐角三角形.直角三角形,钝角三角形.
(2)四边形:任意四边形,平行四边形,梯形.
(3)圆形:扇形.
3.正方形的特征及性质
【知识点归纳】
1.概念:有一组邻边相等且一个角是直角的平行四边形叫做正方形.
2.性质:
(1)边:两组对边分别平行;四条边都相等;相邻边互相垂直
(2)内角:四个角都是90°;
(3)对角线:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角;
(4)对称性:既是中心对称图形,又是轴对称图形(有四条对称轴).
(5)正方形具有平行四边形、菱形、矩形的一切性质.
(6)特殊性质:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
(7)正方形是特殊的长方形.
4.四边形的特点、分类及识别
【知识点归纳】
1.四边形的特点:四边形就是四条线段围成的图形,有四条边,四个角,且内角和是360°.
2.四边形的分类:
任意四边形:图形没有平行的边
平行四边形:图形两组平行的边
梯形:图形只有一组平行的边
3.四边形的识别:
根据分类特地进行识别即可.
5.三角形的分类
【知识点归纳】
1.按角分
判定法一:
锐角三角形:三个角都小于90°.
直角三角形:可记作Rt△.其中一个角必须等于90°.
钝角三角形:有一个角大于90°.
判定法二:
锐角三角形:最大角小于90°.
直角三角形:最大角等于90°.
钝角三角形:最大角大于90°.
其中锐角三角形和钝角三角形统称为斜三角形.
2.按边分
不等边三角形;
等腰三角形;
等边三角形.
6.三角形的内角和
【知识点归纳】
三角形内角和为180°.
直角三角形的两个锐角互余.
7.三角形边的关系
【知识点归纳】
1、两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
2、三角形任意两边的和大于第三边。
8.平行四边形的特征及性质
【知识点归纳】
平行四边形的概念:
1.两组对边分别平行的四边形叫做平行四边形.
平行四边形用符号“ ABCD”,如平行四边形ABCD记作“ ABCD”.
(1)平行四边形属于平面图形.
(2)平行四边形属于四边形.
(3)平行四边形中还包括特殊的平行四边形:矩形,正方形和菱形等.
(4)平行四边形属于中心对称图形.
2.平行四边形的性质:
主要性质
(矩形、菱形、正方形都是特殊的平行四边形.)
(1)如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等.
(简述为“平行四边形的两组对边分别相等”)
(2)如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等.
(简述为“平行四边形的两组对角分别相等”)
(3)夹在两条平行线间的平行线段相等.
(4)平行四边形的面积等于底和高的积.(可视为矩形)
(5)过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形.
(6)平行四边形是中心对称图形,对称中心是两对角线的交点.
(7)平行四边形不是轴对称图形,矩形和菱形是轴对称图形.
注:正方形,矩形以及菱形也是一种特殊的平行四边形,三者具有平行四边形的性质.
9.梯形的特征及分类
【知识点归纳】
1.概念:梯形是指一组对边平行而另一组对边不平行的四边形.
2.分类:
(1)直角梯形:有一个角为直角的梯形为直角梯形
(2)等腰梯形:两腰相等的梯形叫做等腰梯形
(3)一般梯形.
一.选择题(共7小题)
1.这学期我们又认识了很多平面图形,它们之间有着密切的联系。下面选项中,表示它们之间关系错误的是( )
A. B.
C. D.
2.信封盖住了图形的一部分,可能是平行四边形的是( )
A. B. C. D.
3.把平角分成两个角,已知其中一个角是锐角,那么另一个角是( )
A.锐角 B.直角 C.钝角
4.小雪准备用整厘米的小棒摆三角形,她先拿了两根分别是6厘米和8厘米的小棒,正准备拿第三根小棒时,应该是多少厘米?”,她思索片刻( )厘米。
A.10cm B.14cm C.13cm D.16cm
5.数学活动课上,淘气用一条橡皮筋在钉子板上围成如图的四边形。将A点分别拉动至B、C、D、E这4个点的位置后会得到新图形。下面四位同学的说法错误的是( )
A.拉动A点至B点出现的是梯形。
B.拉动A点至E点出现的是直角三角形。
C.拉动A点至C点出现的是平行四边形。
D.拉动A点至D点出现的是梯形。
6.如图,用四根小棒摆成了一个平行四边形,要画出与这个平行四边形完全一样的平行四边形( )
A.一组对边的长度
B.相邻两条边的长度
C.相邻两条边的长度和它们之间夹角的大小
D.四条边的长度
7.用四根木条钉成一个长方形,用手拉动一组对边,使它变成一个平行四边形( )
A.周长不变,面积也不变
B.周长变大,面积也变大
C.周长变小,面积也变小
D.周长不变,面积变小
二.填空题(共6小题)
8.
有 个,
有 个,
有 个,
有 个。
9.任意一个三角形,最多有 个锐角,最少有 个锐角;任意一个三角形,最多有 个钝角,最少有 个钝角。
10.通过研究发现当梯形的上底和下底 时就成了平行四边形,当梯形的上底 时就成了三角形。
11.下面是7根小棒的长度,用来围四边形。
上面的①~⑦根小棒,能围成平行四边形的4根小棒是 ;能围成等腰梯形的4根小棒是 。(填序号)
12.梯形有 组对边互相平行,平行四边形有 组对边互相平行。平行四边形具有 的特性,请写出一个生活中利用这一特性的事例: 。
13.在直角三角形中,其中一个锐角是a°,另一个锐角是 。
三.判断题(共7小题)
14.四边形的对边相等.
15.一个梯形上底与下底间的距离处处相等.
16.钝角三角形的内角和等于锐角三角形的内角和。
17.正方形的两组对边分别平行.
18.平行四边形有无数条高,所有的高都相等.
19.4个角都是直角的四边形一定是正方形.
20.长方形与正方形都是四边形。
四.计算题(共1小题)
21.求出下面三角形中未知角的度数.
五.应用题(共8小题)
22.王师傅用一根70厘米长的木条做了一个平行四边形框架,其中一条边的长是20厘米,另一条边长是多少厘米?
23.向阳小学要举行一次风筝比赛。设计要求这个风筝的造型是等腰三角形,它的一个底角是42°,计算一下这个风筝的顶角是多少度?
24.兰兰不小心打碎了一块三角形的玻璃,现在要配一个完全一样的玻璃,那么兰兰只需要带其中哪一块就可以?
25.一个三角形中,∠A的度数是27.5°,∠B的度数是∠A的1.6倍
26.一个等腰三角的一个顶角是64°,它的一个底角是多少度?如果它的底角是64°,那么它的顶角是多少度?
27.一个等腰三角形的其中一个内角是76°,这个等腰三角形的另外两个内角分别是多少度?
28.曲米有两根同样长的小棒,长5dm,如果她想用3根小棒摆成一个三角形(取整分米数)?曲婷给了她一根小棒,结果摆成的三角形一个底角是35°。顶角是多少度?
29.小嘉有一个等腰三角形的风筝,它的一个底角是75°,它的顶角是多少度?
第二单元认识三角形和四边形(知识精讲+典题精练)-2023-2024学年四年级下册(北师大版)
参考答案与试题解析
一.选择题(共7小题)
1.【答案】D
【分析】根据平行四边形的对边平行且相等,梯形只有一组对边平行,所以平行四边形不包含梯形,据此解答即可。
【解答】解:分析可知,它们之间关系错误的是。
故选:D。
【点评】本题考查了平行四边形和梯形的特征,结合题意分析解答即可。
2.【答案】A
【分析】两组对边分别平行的四边形叫做平行四边形,据此解答。
【解答】解:信封盖住了图形的一部分,可能是平行四边形的是。
故选:A。
【点评】本题考查了平行四边形的特征。
3.【答案】C
【分析】根据锐角、直角、钝角、平角的意义,小于90度的角叫做锐角;等于90度的角叫做直角;等于90度小于180度的角叫做钝角,等于180度的角叫做平角.据此解答即可.
【解答】解:由分析可知:平角=锐角+钝角,
答:把平角分成两个角,已知其中一个角是锐角.
故选:C.
【点评】此题考查的目的是理解掌握锐角、直角、钝角、平角的意义.
4.【答案】C
【分析】根据三角形两边之和大于第三边,两边之差小于第三边,解答此题即可。
【解答】解:8厘米﹣6厘米=4厘米
8厘米+6厘米=14厘米
4厘米<第三边<14厘米
答:她拿的第三根小棒长度是13厘米。
故选:C。
【点评】熟练掌握三角形的三边关系,是解答此题的关键。
5.【答案】A
【分析】梯形是指一组对边平行而另一组对边不平行的四边形,两组对边分别平行的四边形叫做平行四边形,有一个角是直角的三角形是直角三角形,据此解答即可。
【解答】解:A. 拉动A点至B点出现的不是梯形,所以本选项说法错误。
B. 拉动A点至E点出现的是直角三角形,所以本选项说法正确。
C. 拉动A点至C点出现的是平行四边形,所以本选项说法正确。
D. 拉动A点至D点出现的是梯形,所以本选项说法正确。
故选:A。
【点评】本题考查了梯形、直角三角形、平行四边形的特征和认识,结合题意分析解答即可。
6.【答案】C
【分析】根据平行四边形的对边平行且相等,用四根小棒摆成了一个平行四边形,要画出与这个平行四边形完全一样的平行四边形,需要知道这个平行四边形相邻两条边的长度和它们之间夹角的大小,据此解答即可。
【解答】解:用四根小棒摆成了一个平行四边形,要画出与这个平行四边形完全一样的平行四边形。
故选:C。
【点评】本题考查了平行四边形的特征和画法,结合题意分析解答即可。
7.【答案】D
【分析】根据长方形和平行四边形的特征和性质可知,把一个长方形框架拉成一个平行四边形,四条边的长度不变,只是高变小了;所以根据周长的求法,可知周长不变;根据面积的求法,可知面积变小了;据此解答。
【解答】解:把一个长方形拉成一个平行四边形,四条边的长度不变;所以周长不变。
故选:D。
【点评】解决此题的关键是弄清:把一个长方形拉成一个平行四边形,四条边的长度不变,只是高变小了。
二.填空题(共6小题)
8.【答案】3;3;3;4。
【分析】根据正方体、长方体、圆柱、球的特征进行分类识别,再数出相应的数量即可。
【解答】解:有3个,
有3个,
有3个,
有4个。
故答案为:3;4;3;4。
【点评】本题考查了正方体、长方体、圆柱、球的特征,从而进行分类识别。
9.【答案】3;2;1;0。
【分析】根据三角形的内角和是180度,锐角:大于0°,小于90°的角;钝角:大于90°,小于180°的角;进行解答即可。
【解答】解:任意一个三角形,最多有3个锐角;任意一个三角形,最少有0个钝角。
故答案为:5;2;1;8。
【点评】此题考查了三角形的内角和及钝角、锐角的概念,结合题意分析解答即可。
10.【答案】相等,为0。
【分析】如图:
由图可知:当梯形的上底逐渐缩小到一点时,梯形就转化成三角形;当梯形的上底增大到与下底相等时,梯形就转化成平行四边形,据此解答即可。
【解答】解:研究发现当梯形的上底和下底相等时就成了平行四边形,当梯形的上底为0时就成了三角形。
故答案为:相等,为0。
【点评】本题考查了三角形、梯形和平行四边形的特征,解答此题的关键是通过画图,进行分析,继而得出结论。
11.【答案】①②③④; ③④⑤⑥。(答案不唯一)
【分析】平行四边形的对边平行且相等,等腰梯形的两条腰相等,且上下底互相平行,据此解答。
【解答】解:上面的①~⑦根小棒,能围成平行四边形的4根小棒是①②③④。
故答案为:①②③④; ③④⑤⑥
【点评】本题考查了平行四边形及等腰梯形的特征。
12.【答案】一,两,易变形,平行四边形伸缩门(答案不唯一)。
【分析】根据平行四边形、梯形的特征,可得平行四边形的两组对边互相平行,并且相等,梯形只有一组对边互相平行;
平行四边形具有易变形的特性,生活中的平行四边形伸缩门就利用这个特性制作,据此解答。
【解答】解:梯形有一组对边互相平行,平行四边形有两组对边互相平行,生活中的平行四边形伸缩门就利用这个特性制作
故答案为:一,两,易变形。
【点评】此题主要考查了平行四边形、梯形的特征和应用,要熟练掌握,解答此题的关键是要明确:平行四边形的两组对边互相平行,并且相等,梯形只有一组对边互相平行,平行四边形具有易变形的特性。
13.【答案】(90﹣a)°。
【分析】根据三角形的内角和是180度可知,直角三角形中两个锐角的和是90度;用90度减去其中一个锐角的度数,就是另一个锐角的度数。
【解答】解:在一个直角三角形中,其中一个锐角是a度。
故答案为:(90﹣a)°。
【点评】本题考查了三角形的内角和,掌握三角形的内角和以及用含字母的式子表示数量关系是解题的关键。
三.判断题(共7小题)
14.【答案】×
【分析】在同一平面内,由不在同一直线上四条线段依次首尾相接围成的封闭的图形叫做四边形,由此即可判断.
【解答】解:由分析可知,四边形的对边不一定相等;
故答案为:×.
【点评】此题主要考查四边形与正方形的定义.
15.【答案】见试题解答内容
【分析】因为梯形的上下底是平行的,所以夹在两平行线之间的距离是处处相等,据此可知:梯形上底与下底间的距离处处相等的说法是正确的.
【解答】解:梯形上底与下底间的距离就是这个梯形的高,所以处处相等的说法是正确的.
故判断为:√.
【点评】此题考查梯形的特征,即上下底平行,还要明确夹在两平行线之间的距离是处处相等的.
16.【答案】√
【分析】根据任何三角形内角和都是180°即可解决。
【解答】解:因为任何三角形内角和都是180°,所以原题说法是正确的。
故答案为:√。
【点评】此题考查了三角形的内角和是180°。
17.【答案】√
【分析】四条边都相等的是正方形;也就是说:正方形的两组对边分别平行,它是特殊的平行四边形;由此解答即可.
【解答】解:正方形的两组对边分别平行,说法正确;
故答案为:√.
【点评】此题应根据正方形的特征进行解答.
18.【答案】见试题解答内容
【分析】根据平行四边行的定义可知,有两组对边平行的四边行叫平行四边形,平行四边形的高为两组边的距离,所以平行四边形有两组高,每组的高都相等且有无数条.
【解答】解:根据平行四边行的定义可知,有两组对边平行的四边行叫平行四边形,所以平行四边形有两组高;
所以上面的说法是错误的.
故答案为:×.
【点评】此题考查了平行四边形高的有关知识.
19.【答案】×
【分析】根据正方形的特征及性质可知:具有四条边都相等且四个角都是直角的四边形为正方形,据此判断即可.
【解答】解:因为四边相等,四个角都角是直角的四边形是正方形,
所以题干的说法不全面,四个角都是直角的四边形还可能是长方形,
因此题干的说法是错误的;
故答案为:×.
【点评】本题主要考查正方形的特征及性质.
20.【答案】√
【分析】四边形就是四条线段围成的图形,有四条边,四个角。
【解答】解:长方形与正方形都是四边形。原题说法正确。
故答案为:√。
【点评】本题考查了四边形的特征。
四.计算题(共1小题)
21.【答案】见试题解答内容
【分析】根据三角形的内角和是180°,用180°减去已知的2个角的度数,就是要求的角的度数,列式解答即可.
【解答】解:∠1=180°﹣70°﹣38°
=110°﹣38°
=72°
答:∠1等于72度.
180°﹣120°﹣30°
=60°﹣30°
=30°
答:第三个角等于30度.
∠6=180°﹣90°﹣30°
=90°﹣30°
=60°
答:∠1等于60度.
180°﹣90°﹣60°
=90°﹣60°
=30°
答:第三个角等于30度.
【点评】本题考查的是三角形的内角和的运用,注意直角等于90°,三角形的内角和等于180°.
五.应用题(共8小题)
22.【答案】见试题解答内容
【分析】70厘米即围成平行四边形的周长,根据平行四边形特征:两组对边分别相等,所以平行四边形的周长等于两条相邻边的和乘2,即可解答.
【解答】解:70÷2﹣20
=35﹣20
=15(厘米)
答:另一条边长是15厘米.
【点评】此题应结合题意,并根据平行四边形的特点进行分析、解答.
23.【答案】96度。
【分析】根据三角形的内角和等于180°和等腰三角形的两个底角相等,解答此题即可。
【解答】解:180°﹣42°×2
=180°﹣84°
=96°
答:这个风筝的顶角是96度。
【点评】熟练掌握三角形的内角和定理,是解答此题的关键。
24.【答案】见试题解答内容
【分析】根据三角形的内角和定理,可由两个已知角算出第三个内角的度数,而只有第三块玻璃含有2个内角,据此解答即可.
【解答】解:兰兰不小心打碎了一块三角形的玻璃,现在要配一个完全一样的玻璃.
答:兰兰只需要带第3块就可以.
【点评】解答此题的关键是明确第3块玻璃不仅含有2个内角还含有三角形的一条完整的边,这样配出的三角形玻璃就与原来的玻璃完全一样.
25.【答案】见试题解答内容
【分析】根据题意,先利用“求一个数的几倍是多少,用乘法计算”,求∠B的度数;然后利用三角形内角和定理:三角形的内角和是180°,求∠C的度数,进而判断三角形的形状.
【解答】解:∠B=27.5°×1.6=44°
∠C=180°﹣(27.5°+44°)=108.5°
108.8°>90°
答:∠C=108.5°,这是一个钝角三角形.
【点评】本题主要考查三角形的内角和,关键利用三角形内角和定理做题.
26.【答案】58°;52°。
【分析】三角形内角和等于180°,等腰三角形的两个底角相等;180°减顶角的度数,再除以2等于一个底角的度数;180°减两个底角的度数,等于顶角的度数;据此即可解答。
【解答】解:(180°﹣64°)÷2
=116°÷2
=58°
180°﹣64°×5
=180°﹣128°
=52°
答:一个等腰三角的一个顶角是64°,它的一个底角是58°,它的顶角是52°。
【点评】本题主要考查学生对三角形的内角和及等腰三角形的特征的掌握和灵活运用。
27.【答案】52°、52°或76°、28°。
【分析】根据三角形的内角和是180°,当76°是顶角时,用180°减去76°,再除以2,求出底角的度数;当76°是底角时,用三角形的内角和减去两个76°就是顶角的度数。
【解答】解:(180°﹣76°)÷2
=104°÷2
=52°
180°﹣76°×4
=180°﹣152°
=28°
答:这个等腰三角形的另外两个内角是52°、52°或76°。
【点评】熟练掌握三角形的内角和以及等腰三角形的特征是解题的关键。
28.【答案】9分米;110度。
【分析】根据三角形任意两边之和大于第三边,和三角形的内角和等于180°,解答此题即可。
【解答】解:第3根小棒<5+2
第三根小棒<10(分米)
答:第3根小棒最长是9分米。
180°﹣35°×5
=180°﹣70°
=110°
答:顶角是110度。
【点评】熟练掌握三角形的三边关系和三角形内角和定理,是解答此题的关键。
29.【答案】30 度。
【分析】根据三角形的内角和等于180°和等腰三角形的两个底角相等,解答此题即可。
【解答】解:180﹣2×75
=180﹣150
=30(度)
答:它的顶角是 30 度。
【点评】熟练掌握三角形的内角和,是解答此题的关键。
