苏教版数学选修2-3离散型随机变量的数学期望
文档属性
| 名称 | 苏教版数学选修2-3离散型随机变量的数学期望 |

|
|
| 格式 | rar | ||
| 文件大小 | 158.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-17 00:00:00 | ||
图片预览



文档简介
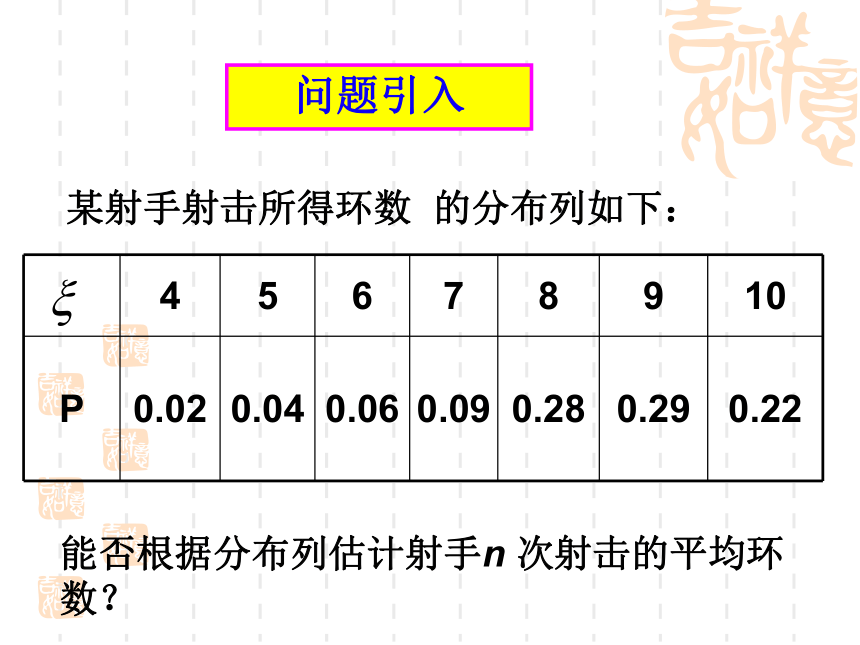
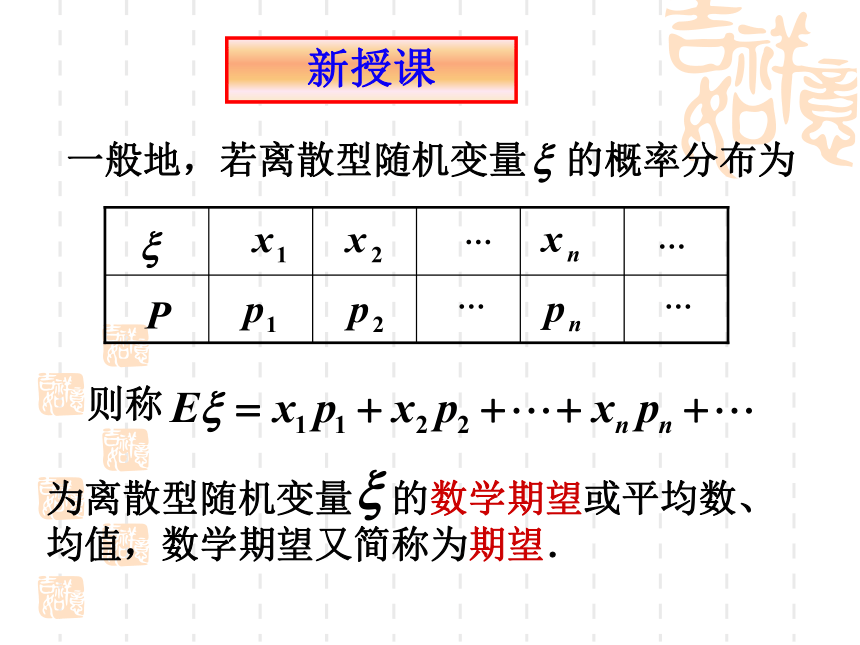
课件11张PPT。离散型随机变量的数学期望学习目标(1)理解数学期望所表达的实际意义 (2)数学期望的求法(3)常见分布的数学期望的求法问题引入某射手射击所得环数 的分布列如下:能否根据分布列估计射手n 次射击的平均环数?新授课一般地,若离散型随机变量 的概率分布为 则称为离散型随机变量 的数学期望或平均数、
均值,数学期望又简称为期望.注意:(1)随机变量的数学期望反映的是离散型
随机变量的平均水平(2)求随机变量的期望关键在于写出它
的分布列例题讲解思考:例题中的随机变量属于什么类型的分布?
数学期望值与罚球命中的概率p相等吗?
有没有一般的结论?
例题讲解例2,高二(4)班的联欢会上设计了一项戏,在一个口袋中一共装有10个球,其中有2个红球,8个白球,这些球除了颜色外完全同,某学生一次从中摸出3个球,其中红球的个数为X,求X的数学期望.思考:例题中的随机变量服从什么分布?超几何分布
的数学期望有没有一般结论?例题讲解例3:求随机抛掷均匀硬币5次,随机变量X表示出现正面的次数,求随机变量的X的数学期望思考:问题中的X服从什么分布?你有什么发现?
二项分布的数学期望有一般的结论吗?证明:服从二项分布 的随机变量的期望所以,证明:为 1、随机变量的数学期望实际意义。
2、几种常见分布的数学期望
①若ξ~B(n,p),则Eξ=np
②若ξ~两点分布,则Eξ=p
③若ξ~H(n,M,N),则课堂小结课堂练习3.一袋中有6个球,编号为1,2,3,4,56,在袋中同时取3个,则三只球中的最大号码X的数学期望2.已知100个产品中有10个次品,求任意取出5个产品中的次品数的数学期望
均值,数学期望又简称为期望.注意:(1)随机变量的数学期望反映的是离散型
随机变量的平均水平(2)求随机变量的期望关键在于写出它
的分布列例题讲解思考:例题中的随机变量属于什么类型的分布?
数学期望值与罚球命中的概率p相等吗?
有没有一般的结论?
例题讲解例2,高二(4)班的联欢会上设计了一项戏,在一个口袋中一共装有10个球,其中有2个红球,8个白球,这些球除了颜色外完全同,某学生一次从中摸出3个球,其中红球的个数为X,求X的数学期望.思考:例题中的随机变量服从什么分布?超几何分布
的数学期望有没有一般结论?例题讲解例3:求随机抛掷均匀硬币5次,随机变量X表示出现正面的次数,求随机变量的X的数学期望思考:问题中的X服从什么分布?你有什么发现?
二项分布的数学期望有一般的结论吗?证明:服从二项分布 的随机变量的期望所以,证明:为 1、随机变量的数学期望实际意义。
2、几种常见分布的数学期望
①若ξ~B(n,p),则Eξ=np
②若ξ~两点分布,则Eξ=p
③若ξ~H(n,M,N),则课堂小结课堂练习3.一袋中有6个球,编号为1,2,3,4,56,在袋中同时取3个,则三只球中的最大号码X的数学期望2.已知100个产品中有10个次品,求任意取出5个产品中的次品数的数学期望
