北京市三帆中学2023—2024学年下学期九年级开学考数学试卷(pdf版 无答案)
文档属性
| 名称 | 北京市三帆中学2023—2024学年下学期九年级开学考数学试卷(pdf版 无答案) |  | |
| 格式 | |||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 18:30:13 | ||
图片预览



文档简介
班级 分层班级 学号 姓名
北京三帆中学第二学期初三数学阶段性学习反馈
注意:(1)时间 120分钟,满分 100分;(2)答案一律填写在答题纸上.
一、选择题(本题共 16分,每小题 2分)
1. 抛物线 y=x2-2mx+3的对称轴为直线 x=2,则 m的值为( )
A. -2 B. 2 C.-4 D.4
2. 围棋起源于中国,古代称之为“弈”,至今已有 4000多年的历史.2017年 5月,世界围棋冠
军柯洁与人工智能机器人 AlphaGo 进行围棋人机大战.截取首局对战棋谱中的四个部分,
由黑白棋子摆成的图案是中心对称的是( )
A. B. C. D.
3. 在 Rt△ABC中, C 90 , AB 5 , AC 2,则 tanB的值为( )
1 5 2 5
A. B. 2 C. D.
2 5 5
4.下列函数中,当 x 0时, y随 x的增大而增大的是( )
3 4
A. y=-x2+3 B. y=-2x+5 C. y D. y
x x
5. 大约在两千四五百年前,墨子和他的学生做了世界上第一个小孔成倒像的实验,如图 1,并在
《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”. 翻译:影像倒立,在光
线交会处有一小孔; 关于影像的大小,在于小孔相对物、像的位置.
图 1 图 2
在如图 2所示的小孔成像实验中,若物距为 10cm,像距为 15cm,则蜡烛火焰倒立的像的
高度与蜡烛火焰的高度的比为( )
A.1:1 B.2:1 C.2:3 D.3:2
1 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
6. 一个不透明的盒子里装有红色和白色的小球共 20个,除颜色外无其它区别,随机摸出一个
小球,记录颜色后放回并摇匀,再随机摸出一个,下图是某数学学习小组开展上述摸球活动
的实验结果,下列推断合理的是( )
A. 当摸球次数是 300时,记录“摸到红球”的次数是 99,所以“摸到红球”的概率是 0.33;
B. 若再次开展上述摸球活动,则当摸球次数为 500时,“摸到红球”的概率一定是 0.40;
C. 随着试验次数的增加,“摸到红球”的频率总在 0.35附近摆动,显示出一定的稳定性,可
以估计“摸到红球”的概率是 0.35;
D. 可以根据本次实验结果,计算出盒子中约有红球 8个.
7. 如图,点 O为线段 AB的中点,点 B,C,D到点 O的距离相等,
连接 AC,BD. 则下面结论不.一.定.成立的是( )
A.∠ACB=∠ADB B. ∠ABC+∠ADC=180°
C.∠ABD=∠ACD D. 若∠ABD=2∠CBD ,则 AD=2CD
8. 如图,抛物线 y ax2 bx c(a 0)的对称轴是直线 x=1,其部分图象如图,则下面结论中:
① bc<0; ② 2a+b=0; ③ 3a+c>0; ④ 4a+b2>4ac;
⑤ 若点 P(m,n)在此抛物线上,且 n<c,则 m<0.
所有正确结论的序号为( )
A. ①② B. ②④ C. ②③ D.④⑤
二、填空题(本题共 16分,每小题 2分)
9. 2已知关于 x的方程 x 2x m 0有两个不相等的实数根,则 m的取值范围是 .
10. 将抛物线 y=-2x2向右平移 2个单位,向上平移 3个单位得到 .
11. 某小区草坪上的自动喷水装置的旋转角为 200°,且它的喷灌区域是一个扇形.若它能喷灌
的扇形草坪面积为 5π平方米,则这个扇形的半径是 米.
2 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
班级 分层班级 学号 姓名
12.若点(-1,a),(-2,b) 4都在反比例函数 y 的图象上,则 a与 b的大小关系是:a b
x
(填“>”、“=”或“<”).
13. 如图,在△ABC中,点D在 AB上(不与点 A,B重合),连接CD.只
需添加一个条件即可证明△ACD∽△ABC ,这个条件可以是
___________________(写出一个即可).
14. 若关于 x的一元二次方程 (a 1)x2 a2x a 0有一个根是 x=1,则 a=_____.
15. 如图,等边△ABC的边长为 2,点 A,B在⊙O上,点 C在⊙O内,
⊙O的半径为 2 ,将△ABC 绕点 A 逆时针旋转,当 AC 第一次与
⊙O相切时,旋转角为 °.
16. 在平面直角坐标系 xOy中,点 P在 y轴上,点 A(2,0),B(8,0),
⊙Q为△ABP的外接圆.当∠APB最大时,点 P的坐标为 .
三、解答题(共 68分,第 17-19、21-23题各 5分、20、24-26题各 6分、27、28题各 7分)
17.解方程: 2x2 3x 1 0.
18.关于 的一元二次方程 x2-(m+3)x+m+2=0.
(1)求证:方程总有两个实数根;
(2)若方程的两个实数根都是正整数,求 的最小值.
19. 在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个
引理.如图,已知劣弧 AB,C是弦 AB上一点.
(1)根据提示完成尺规作图(保留作图痕迹,不写作法);
①作线段 AC的垂直平分线 DE,分别交劣弧 AB于点 D,垂足为 E;
②以点 D为圆心,DA长为半径作弧,交劣弧 AB于点 F(F,A两点不重合),连接 BF.
(2)引理的结论为:BC=BF.
证明:连接 DA, DC, DF, DB.
∴ DA为 AC的垂直平分线
3 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
∴ DA=DC
∴ ∠DAC=∠DCA
又∵ 四边形 ABFD为圆的内接四边形
∴ ∠DAC+∠_____=180°( )
又∵ ∠DCA+∠DCB=180°
∴ ∠DCB =∠DFB
又∵ AD=FD
∴ AD =
∴ ∠ABD=∠DBF( )
∴ △BCD≌△BFD (AAS)
∴ BC=BF.
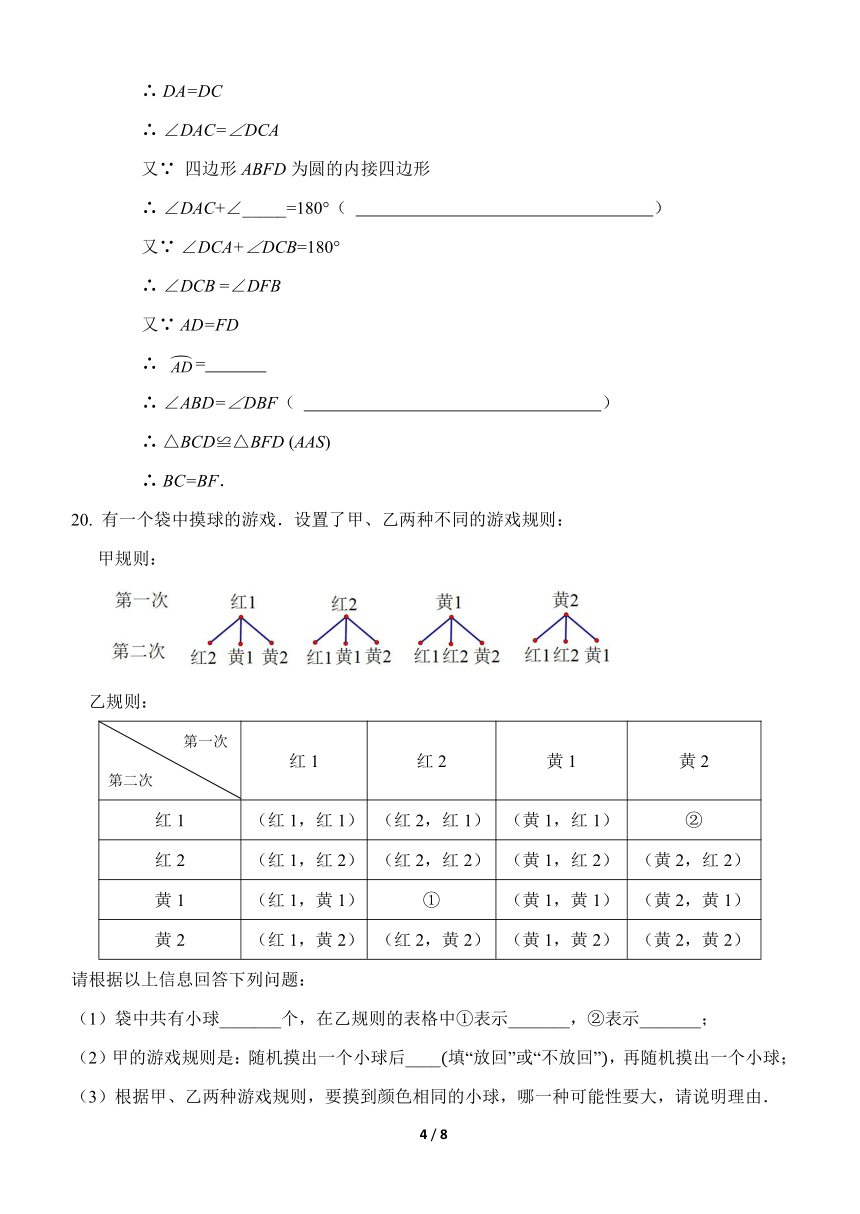
20. 有一个袋中摸球的游戏.设置了甲、乙两种不同的游戏规则:
甲规则:
乙规则:
第一次
红 1 红 2 黄 1 黄 2
第二次
红 1 (红 1,红 1) (红 2,红 1) (黄 1,红 1) ②
红 2 (红 1,红 2) (红 2,红 2) (黄 1,红 2) (黄 2,红 2)
黄 1 (红 1,黄 1) ① (黄 1,黄 1) (黄 2,黄 1)
黄 2 (红 1,黄 2) (红 2,黄 2) (黄 1,黄 2) (黄 2,黄 2)
请根据以上信息回答下列问题:
(1)袋中共有小球_______个,在乙规则的表格中①表示_______,②表示_______;
(2)甲的游戏规则是:随机摸出一个小球后____(填“放回”或“不放回”),再随机摸出一个小球;
(3)根据甲、乙两种游戏规则,要摸到颜色相同的小球,哪一种可能性要大,请说明理由.
4 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
班级 分层班级 学号 姓名
21. 如图,已知二次函数 y x2 ax 3的图象经过点 P(-2,3)
(1)求 a的值和图象的顶点坐标;
(2)点 Q(m,n)在该二次函数图象上.
①当m 2时,求 n的值;
②若点 Q到 y轴的距离小于 2,根据图象直接写出 n的取值范围.
22. 如图,在 Rt△ABC中,∠ACB=90°,AB的中垂线交边 BC于点 E,交 AC的延长线于点 F,
连接 AE.
(1)求证:△ADE∽△FDA;
(2)若 DE=2EF=2,求 AE的长.
23. 如图,在平面直角坐标系 xOy中,直线 y x b与 x轴、
y 3轴分别交于点 A,B.与双曲线 y 的交点为 M,N.
x
(1)当点 M的横坐标为 1时,求b的值;
(2)若MN 2AB,结合函数图象,直接写出 b的取值
范围.
24.如图 AB是⊙O的直径,PB,PC与⊙O分别相切于点 B,C,PC交 BA的延长线于点 D,
DE⊥PO交 PO的延长线于点 E.
(1)求证:∠EPD=∠EDO;
3
(2)若 PC=6,tan∠PDB= ,求 OE的长.
4
5 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
25. “城市轨道交通是现代大城市交通的发展方向,发展轨道交通是解决大城市病的有效途径.”
如图,北京地铁(BeijingSubway)是中华人民共和国北京市的城市轨道交通系统,规划于
1953年,始建于 1965年,运营于 1969年,是中国第一个地铁系统.小华了解到列车从慈寿寺
站开往花园桥站时,在距离停车线 256米处开始减速.他想知道列车从减速开始,经过多少秒
停下来,以及最后一秒滑行的距离.为了解决这个问题,小华通过建立函数模型来描述列车离
停车线的距离 s(米)与滑行时间 t(秒)的函数关系,再应用该函数解决相应的问题.
(1)建立模型
①收集数据
r(秒) 0 4 8 12 16 20 24
s(米) 256 196 144 100 64 36 16
②建立平面直角坐标系
为了观察 s(米)与 t(秒)的关系,建立如图所示的平面直角坐标系;
6 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
班级 分层班级 学号 姓名
③描点连线
请在平面直角坐标系中将表中未描出的点补充完整,并用平滑的曲线依次连接;
④选择函数模型
观察这条曲线的形状,它可能是________函数的图象;
⑤求函数解析式
(2)应用模型
列车从减速开始经过_______秒,列车停止;最后一秒钟,列车滑行的距离为_______米.
26.在平面直角坐标系 xoy中,已知抛物线 y x2 4x c
(1)抛物线经过点 (0, y1)和 (3, y2 ),请比较 y1和 y2的大小;
(2)若抛物线与 x轴的一个交点的坐标为(1,0),
①求抛物线与 x轴的另一个交点的坐标;
②抛物线上两点 A(x0 ,m),B(x0 3,n),满足 mn<0, 求 x0的取值范围.
27. 如图,在△ABC中,AB=AC,点 D是边 BC上的一点,将线段 DB绕点 D顺时针旋转得到
线段 DE,使点 E落在线段 AB上,连接 CE, 点 F为线段 CE的中点,连接 AF,DF.
(1) ①依题意补全图形;
②若 AF⊥DF,判断△ABC的形状,并证明;
(2)若∠BAC=120°,AB=6,当点 D在线段 BC上运动,且 BD≤DC时,线段 AF的最小值
为______________.
7 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
28. 已知平面上的点 P和直线 l1,l2,定义点 P关于直线 l1,l2的“和距离”如下:若点 P到直线
l1,l2的距离分别为 d1,d2,则称 d1+d2为点 P关于直线 l1,l2的“和距离”,记作 dP.特别
地,当点 P在直线 l1上时,d1=0;当点 P在直线 l2上时,d2=0.
若对于不同的两点 P,Q,他们关于直线 l1,l2的“和距离”相等,即 dP=dQ,则称点 P,
点 Q互为“等和距点”.
在平面直角坐标系 xOy中,已知直线 l : y 3x 6 .
(1)若点 P(3,0),则在点 Q1(3,1),Q2(4,-1),Q3(-1,2)中,是点 P关于 x轴和 y轴的“等和距
点”的是___________;
(2)若点 P是直线 y=-x+6上的动点.
① 已知 Q(5,-3)是点 P关于 x轴和 y轴的“等和距点”,则点 P的坐标为__________;
② 对于任一点 P,在直线 y=-x+6上是否都能找到它关于 x轴和直线 l的“等和距点”?说
明理由;
(3)已知点 A(a,0),动点 P在 x轴上方且 PA=1. 若存在点 P,使它关于 x轴和直线 l的“和距
离”dP=6,求 a的取值范围.
8 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
北京三帆中学第二学期初三数学阶段性学习反馈
注意:(1)时间 120分钟,满分 100分;(2)答案一律填写在答题纸上.
一、选择题(本题共 16分,每小题 2分)
1. 抛物线 y=x2-2mx+3的对称轴为直线 x=2,则 m的值为( )
A. -2 B. 2 C.-4 D.4
2. 围棋起源于中国,古代称之为“弈”,至今已有 4000多年的历史.2017年 5月,世界围棋冠
军柯洁与人工智能机器人 AlphaGo 进行围棋人机大战.截取首局对战棋谱中的四个部分,
由黑白棋子摆成的图案是中心对称的是( )
A. B. C. D.
3. 在 Rt△ABC中, C 90 , AB 5 , AC 2,则 tanB的值为( )
1 5 2 5
A. B. 2 C. D.
2 5 5
4.下列函数中,当 x 0时, y随 x的增大而增大的是( )
3 4
A. y=-x2+3 B. y=-2x+5 C. y D. y
x x
5. 大约在两千四五百年前,墨子和他的学生做了世界上第一个小孔成倒像的实验,如图 1,并在
《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”. 翻译:影像倒立,在光
线交会处有一小孔; 关于影像的大小,在于小孔相对物、像的位置.
图 1 图 2
在如图 2所示的小孔成像实验中,若物距为 10cm,像距为 15cm,则蜡烛火焰倒立的像的
高度与蜡烛火焰的高度的比为( )
A.1:1 B.2:1 C.2:3 D.3:2
1 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
6. 一个不透明的盒子里装有红色和白色的小球共 20个,除颜色外无其它区别,随机摸出一个
小球,记录颜色后放回并摇匀,再随机摸出一个,下图是某数学学习小组开展上述摸球活动
的实验结果,下列推断合理的是( )
A. 当摸球次数是 300时,记录“摸到红球”的次数是 99,所以“摸到红球”的概率是 0.33;
B. 若再次开展上述摸球活动,则当摸球次数为 500时,“摸到红球”的概率一定是 0.40;
C. 随着试验次数的增加,“摸到红球”的频率总在 0.35附近摆动,显示出一定的稳定性,可
以估计“摸到红球”的概率是 0.35;
D. 可以根据本次实验结果,计算出盒子中约有红球 8个.
7. 如图,点 O为线段 AB的中点,点 B,C,D到点 O的距离相等,
连接 AC,BD. 则下面结论不.一.定.成立的是( )
A.∠ACB=∠ADB B. ∠ABC+∠ADC=180°
C.∠ABD=∠ACD D. 若∠ABD=2∠CBD ,则 AD=2CD
8. 如图,抛物线 y ax2 bx c(a 0)的对称轴是直线 x=1,其部分图象如图,则下面结论中:
① bc<0; ② 2a+b=0; ③ 3a+c>0; ④ 4a+b2>4ac;
⑤ 若点 P(m,n)在此抛物线上,且 n<c,则 m<0.
所有正确结论的序号为( )
A. ①② B. ②④ C. ②③ D.④⑤
二、填空题(本题共 16分,每小题 2分)
9. 2已知关于 x的方程 x 2x m 0有两个不相等的实数根,则 m的取值范围是 .
10. 将抛物线 y=-2x2向右平移 2个单位,向上平移 3个单位得到 .
11. 某小区草坪上的自动喷水装置的旋转角为 200°,且它的喷灌区域是一个扇形.若它能喷灌
的扇形草坪面积为 5π平方米,则这个扇形的半径是 米.
2 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
班级 分层班级 学号 姓名
12.若点(-1,a),(-2,b) 4都在反比例函数 y 的图象上,则 a与 b的大小关系是:a b
x
(填“>”、“=”或“<”).
13. 如图,在△ABC中,点D在 AB上(不与点 A,B重合),连接CD.只
需添加一个条件即可证明△ACD∽△ABC ,这个条件可以是
___________________(写出一个即可).
14. 若关于 x的一元二次方程 (a 1)x2 a2x a 0有一个根是 x=1,则 a=_____.
15. 如图,等边△ABC的边长为 2,点 A,B在⊙O上,点 C在⊙O内,
⊙O的半径为 2 ,将△ABC 绕点 A 逆时针旋转,当 AC 第一次与
⊙O相切时,旋转角为 °.
16. 在平面直角坐标系 xOy中,点 P在 y轴上,点 A(2,0),B(8,0),
⊙Q为△ABP的外接圆.当∠APB最大时,点 P的坐标为 .
三、解答题(共 68分,第 17-19、21-23题各 5分、20、24-26题各 6分、27、28题各 7分)
17.解方程: 2x2 3x 1 0.
18.关于 的一元二次方程 x2-(m+3)x+m+2=0.
(1)求证:方程总有两个实数根;
(2)若方程的两个实数根都是正整数,求 的最小值.
19. 在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个
引理.如图,已知劣弧 AB,C是弦 AB上一点.
(1)根据提示完成尺规作图(保留作图痕迹,不写作法);
①作线段 AC的垂直平分线 DE,分别交劣弧 AB于点 D,垂足为 E;
②以点 D为圆心,DA长为半径作弧,交劣弧 AB于点 F(F,A两点不重合),连接 BF.
(2)引理的结论为:BC=BF.
证明:连接 DA, DC, DF, DB.
∴ DA为 AC的垂直平分线
3 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
∴ DA=DC
∴ ∠DAC=∠DCA
又∵ 四边形 ABFD为圆的内接四边形
∴ ∠DAC+∠_____=180°( )
又∵ ∠DCA+∠DCB=180°
∴ ∠DCB =∠DFB
又∵ AD=FD
∴ AD =
∴ ∠ABD=∠DBF( )
∴ △BCD≌△BFD (AAS)
∴ BC=BF.
20. 有一个袋中摸球的游戏.设置了甲、乙两种不同的游戏规则:
甲规则:
乙规则:
第一次
红 1 红 2 黄 1 黄 2
第二次
红 1 (红 1,红 1) (红 2,红 1) (黄 1,红 1) ②
红 2 (红 1,红 2) (红 2,红 2) (黄 1,红 2) (黄 2,红 2)
黄 1 (红 1,黄 1) ① (黄 1,黄 1) (黄 2,黄 1)
黄 2 (红 1,黄 2) (红 2,黄 2) (黄 1,黄 2) (黄 2,黄 2)
请根据以上信息回答下列问题:
(1)袋中共有小球_______个,在乙规则的表格中①表示_______,②表示_______;
(2)甲的游戏规则是:随机摸出一个小球后____(填“放回”或“不放回”),再随机摸出一个小球;
(3)根据甲、乙两种游戏规则,要摸到颜色相同的小球,哪一种可能性要大,请说明理由.
4 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
班级 分层班级 学号 姓名
21. 如图,已知二次函数 y x2 ax 3的图象经过点 P(-2,3)
(1)求 a的值和图象的顶点坐标;
(2)点 Q(m,n)在该二次函数图象上.
①当m 2时,求 n的值;
②若点 Q到 y轴的距离小于 2,根据图象直接写出 n的取值范围.
22. 如图,在 Rt△ABC中,∠ACB=90°,AB的中垂线交边 BC于点 E,交 AC的延长线于点 F,
连接 AE.
(1)求证:△ADE∽△FDA;
(2)若 DE=2EF=2,求 AE的长.
23. 如图,在平面直角坐标系 xOy中,直线 y x b与 x轴、
y 3轴分别交于点 A,B.与双曲线 y 的交点为 M,N.
x
(1)当点 M的横坐标为 1时,求b的值;
(2)若MN 2AB,结合函数图象,直接写出 b的取值
范围.
24.如图 AB是⊙O的直径,PB,PC与⊙O分别相切于点 B,C,PC交 BA的延长线于点 D,
DE⊥PO交 PO的延长线于点 E.
(1)求证:∠EPD=∠EDO;
3
(2)若 PC=6,tan∠PDB= ,求 OE的长.
4
5 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
25. “城市轨道交通是现代大城市交通的发展方向,发展轨道交通是解决大城市病的有效途径.”
如图,北京地铁(BeijingSubway)是中华人民共和国北京市的城市轨道交通系统,规划于
1953年,始建于 1965年,运营于 1969年,是中国第一个地铁系统.小华了解到列车从慈寿寺
站开往花园桥站时,在距离停车线 256米处开始减速.他想知道列车从减速开始,经过多少秒
停下来,以及最后一秒滑行的距离.为了解决这个问题,小华通过建立函数模型来描述列车离
停车线的距离 s(米)与滑行时间 t(秒)的函数关系,再应用该函数解决相应的问题.
(1)建立模型
①收集数据
r(秒) 0 4 8 12 16 20 24
s(米) 256 196 144 100 64 36 16
②建立平面直角坐标系
为了观察 s(米)与 t(秒)的关系,建立如图所示的平面直角坐标系;
6 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
班级 分层班级 学号 姓名
③描点连线
请在平面直角坐标系中将表中未描出的点补充完整,并用平滑的曲线依次连接;
④选择函数模型
观察这条曲线的形状,它可能是________函数的图象;
⑤求函数解析式
(2)应用模型
列车从减速开始经过_______秒,列车停止;最后一秒钟,列车滑行的距离为_______米.
26.在平面直角坐标系 xoy中,已知抛物线 y x2 4x c
(1)抛物线经过点 (0, y1)和 (3, y2 ),请比较 y1和 y2的大小;
(2)若抛物线与 x轴的一个交点的坐标为(1,0),
①求抛物线与 x轴的另一个交点的坐标;
②抛物线上两点 A(x0 ,m),B(x0 3,n),满足 mn<0, 求 x0的取值范围.
27. 如图,在△ABC中,AB=AC,点 D是边 BC上的一点,将线段 DB绕点 D顺时针旋转得到
线段 DE,使点 E落在线段 AB上,连接 CE, 点 F为线段 CE的中点,连接 AF,DF.
(1) ①依题意补全图形;
②若 AF⊥DF,判断△ABC的形状,并证明;
(2)若∠BAC=120°,AB=6,当点 D在线段 BC上运动,且 BD≤DC时,线段 AF的最小值
为______________.
7 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
28. 已知平面上的点 P和直线 l1,l2,定义点 P关于直线 l1,l2的“和距离”如下:若点 P到直线
l1,l2的距离分别为 d1,d2,则称 d1+d2为点 P关于直线 l1,l2的“和距离”,记作 dP.特别
地,当点 P在直线 l1上时,d1=0;当点 P在直线 l2上时,d2=0.
若对于不同的两点 P,Q,他们关于直线 l1,l2的“和距离”相等,即 dP=dQ,则称点 P,
点 Q互为“等和距点”.
在平面直角坐标系 xOy中,已知直线 l : y 3x 6 .
(1)若点 P(3,0),则在点 Q1(3,1),Q2(4,-1),Q3(-1,2)中,是点 P关于 x轴和 y轴的“等和距
点”的是___________;
(2)若点 P是直线 y=-x+6上的动点.
① 已知 Q(5,-3)是点 P关于 x轴和 y轴的“等和距点”,则点 P的坐标为__________;
② 对于任一点 P,在直线 y=-x+6上是否都能找到它关于 x轴和直线 l的“等和距点”?说
明理由;
(3)已知点 A(a,0),动点 P在 x轴上方且 PA=1. 若存在点 P,使它关于 x轴和直线 l的“和距
离”dP=6,求 a的取值范围.
8 / 8
{#{QQABKYSUggiAAhBAAAhCEwGaCkOQkBCAAIoGhAAAoAABCBNABAA=}#}
同课章节目录
