5.1.3同位角、内错角、同旁内角 同步练习(含解析)
文档属性
| 名称 | 5.1.3同位角、内错角、同旁内角 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 17:55:49 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版七年级下册数学5.1.1同位角、内错角、同旁内角
同步练习
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.如图,直线AD、BC被直线AC所截,则∠1和∠2是( ).
A.内错角 B.同位角 C.同旁内角 D.对顶角
2.如图,能与构成同位角的有( ).
A.4个 B.3个 C.2个 D.1个
3.下列命题中,真命题有( )
(1)直线外一点与直线上各点连接的所有线段中,垂线段最短;
(2)两条直线被第三条直线所截,内错角相等;
(3)经过两点有一条直线,并且只有一条直线;
(4)如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直.
A.1个 B.2个 C.3个 D.4个
4.若∠1与∠2是同位角,则它们之间的关系是( ).
A.∠1=∠2 ; B.∠1>∠2 ;
C.∠1<∠2; D.∠1=∠2或∠1>∠2或∠1<∠2.
5.如图所示,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
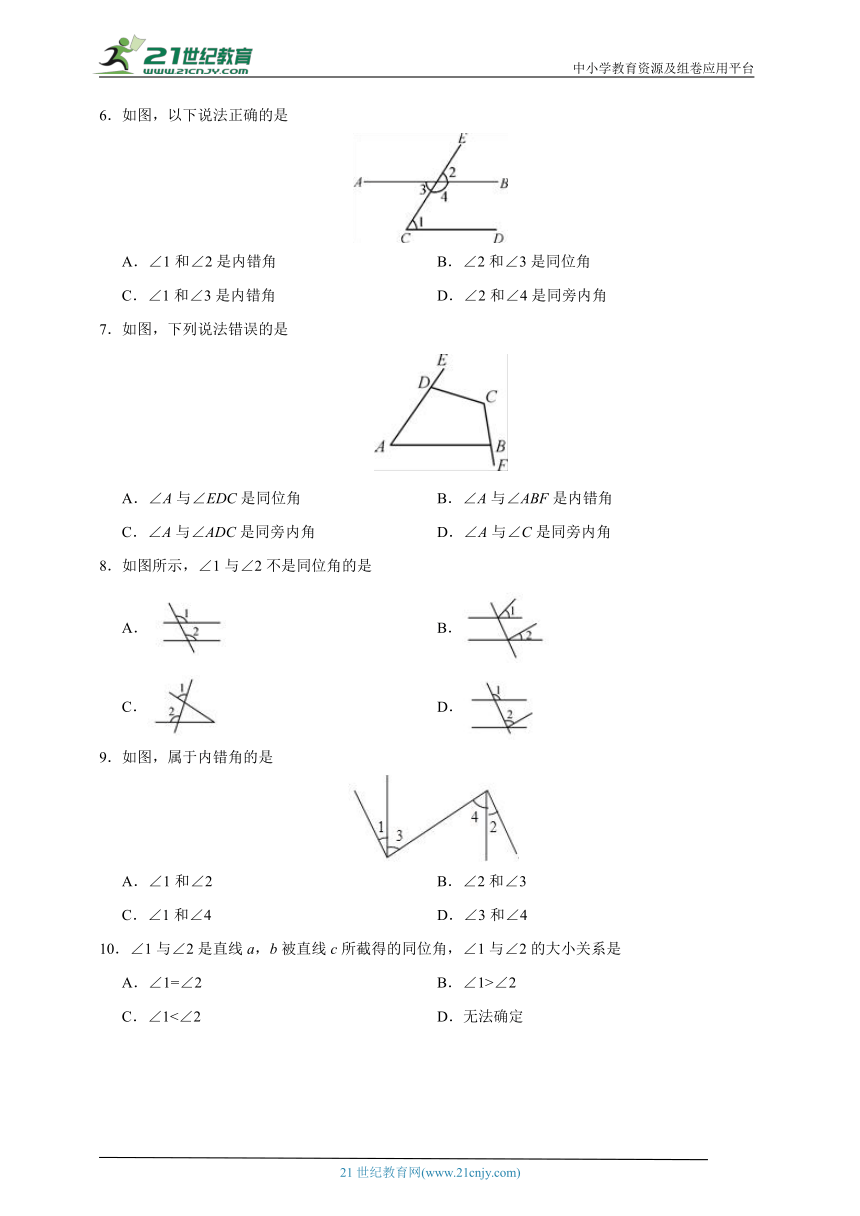
6.如图,以下说法正确的是
A.∠1和∠2是内错角 B.∠2和∠3是同位角
C.∠1和∠3是内错角 D.∠2和∠4是同旁内角
7.如图,下列说法错误的是
A.∠A与∠EDC是同位角 B.∠A与∠ABF是内错角
C.∠A与∠ADC是同旁内角 D.∠A与∠C是同旁内角
8.如图所示,∠1与∠2不是同位角的是
A. B.
C. D.
9.如图,属于内错角的是
A.∠1和∠2 B.∠2和∠3
C.∠1和∠4 D.∠3和∠4
10.∠1与∠2是直线a,b被直线c所截得的同位角,∠1与∠2的大小关系是
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
二、填空题(本大题共5小题,每小题4分,共20分。)
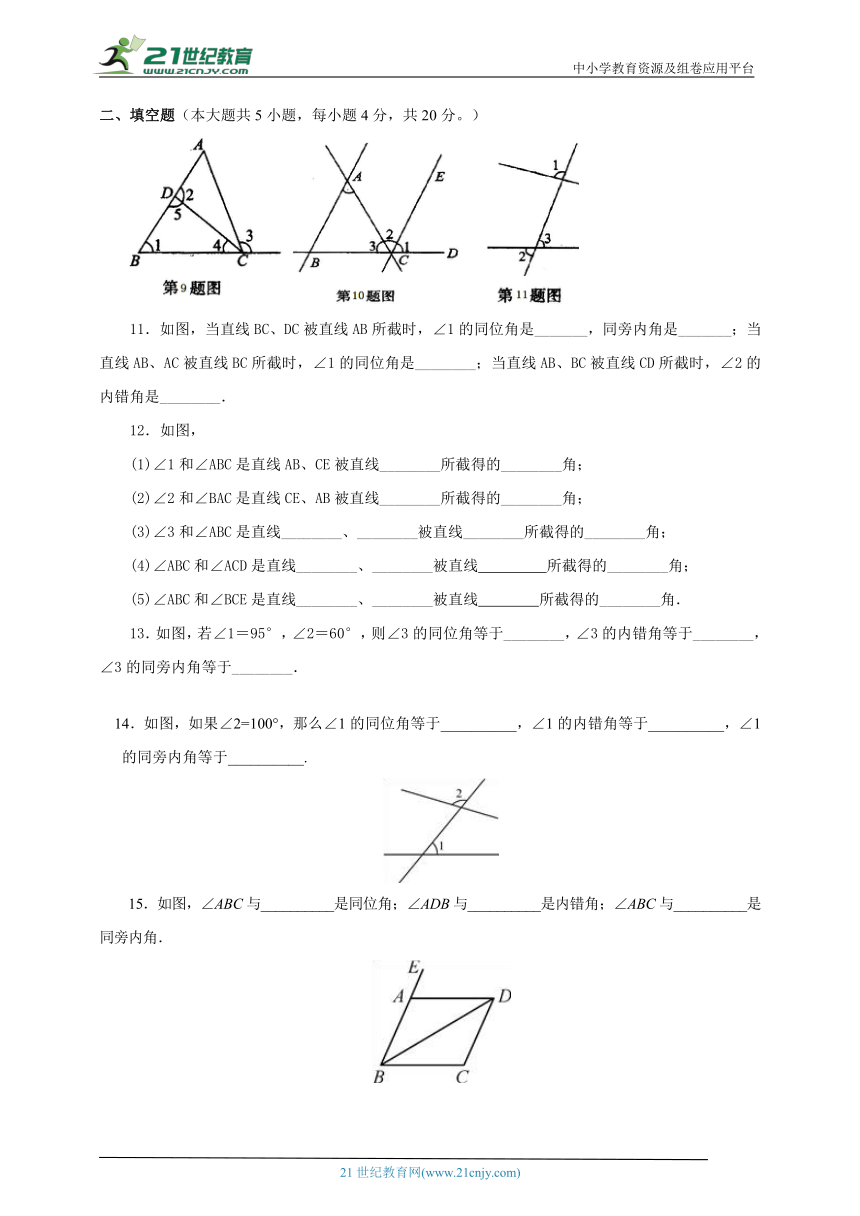
11.如图,当直线BC、DC被直线AB所截时,∠1的同位角是_______,同旁内角是_______;当直线AB、AC被直线BC所截时,∠1的同位角是________;当直线AB、BC被直线CD所截时,∠2的内错角是________.
12.如图,
(1)∠1和∠ABC是直线AB、CE被直线________所截得的________角;
(2)∠2和∠BAC是直线CE、AB被直线________所截得的________角;
(3)∠3和∠ABC是直线________、________被直线________所截得的________角;
(4)∠ABC和∠ACD是直线________、________被直线 所截得的________角;
(5)∠ABC和∠BCE是直线________、________被直线 所截得的________角.
13.如图,若∠1=95°,∠2=60°,则∠3的同位角等于________,∠3的内错角等于________,∠3的同旁内角等于________.
14.如图,如果∠2=100°,那么∠1的同位角等于__________,∠1的内错角等于__________,∠1的同旁内角等于__________.
15.如图,∠ABC与__________是同位角;∠ADB与__________是内错角;∠ABC与__________是同旁内角.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,∠1和哪些角是内错角 ∠1和哪些角是同旁内角 ∠2和哪些角是内错角 ∠2和哪些角是同旁内角 它们分别是由哪两条直线被哪一条线截成的
17.指出图中的同位角、内错角、同旁内角.
18.指出图中各对角的位置关系:
(1)∠C和∠D是 角;
(2)∠B和∠GEF是 角;
(3)∠A和∠D是 角;
(4)∠AGE和∠BGE是 角;
(5)∠CFD和∠AFB是 角.
19.如图:
(1)找出直线DC,AC被直线BE所截形成的同旁内角;
(2)指出∠DEF与∠CFE是由哪两条直线被哪一条直线所截形成的什么角;
(3)试找出图中与∠DAC是同位角的所有角.
20.如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.
一、选择题
1. 【答案】A
【解析】∠1与∠2是直线AD、BC被直线AC所截而成,且这两角都在被截线AD、BC之间,在截线AC两侧,所以为内错角.
2.【答案】B
【解析】如图,与能构成同位角的有:∠1,∠2,∠3.
3. 【答案】B
【解析】(1)直线外一点与直线上各点连接的所有线段中,垂线段最短,正确;
(2)应为两条平行直线被第三条直线所截,内错角相等,故本选项错误;
(3)经过两点有一条直线,并且只有一条直线,正确;
(4)应为如果一条直线和两条平行直线中的一条垂直,那么这条直线也和另一条垂直,故本选项错误.
所以(1)(3)两项是真命题.
4. 【答案】D
【解析】由两角是同位角,内错角或同旁内角得不出它们大小之间的关系.
5. 【答案】A.
6.【答案】C
【解析】观察图形可得,∠1和∠2是同位角、∠2和∠3是对顶角、∠1和∠3是内错角、∠2和∠4是邻补角,所以正确的答案为C,故选C.
7.【答案】D
8.【答案】B
【解析】A中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
B中,∠1与∠2的两条边都不在同一条直线上,不是同位角,符合题意;
C中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
D中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意.
故选B.
9.【答案】D
10.【答案】D
【解析】因为不知道直线a、b之间的位置关系,所以∠1与∠2的大小关系无法确定.故选D.
填空题
11【答案】∠2, ∠5, ∠3, ∠4
【解析】先看哪两条线被哪一条线所截,再判断它们的关系.
12.【答案】(1)BD(或BC), 同位; (2)AC, 内错; (3)AB, AC, BC, 同旁内;
(4)AB, AC, BC,同位; (5)AB, CE, BC,同旁内.
【解析】可以从复杂图形中抽出简单图形进行分析.
13.【答案】85°, 85°, 95°
【解析】∠3的同位角和内错角均与∠1互补,故它们的度数均为:180°-95°=85°,
而∠3的同旁内角是∠1的对顶角,所以∠3的同旁内角的度数等于∠1的度数.
14.
【答案】80°,80°,100°
15.
【答案】∠EAD,∠DBC和∠EAD,∠DAB和∠BCD
【解析】根据同位角,内错角和同旁内角的概念进行判断,
(1) EMBED Equation.DSMT4 与是同位角;
(2)与是内错角;
(3)与是同旁内角.
故答案为:∠EAD,∠DBC和∠EAD,∠DAB和∠BCD.
三、解答题
16. 【解析】
解:∠1和∠DAB是内错角,由直线DE和BC被直线AB所截而成;
∠1和∠BAC是同旁内角,由直线BC和AC被直线AB所截而成;
∠1和∠2也是同旁内角,是直线AB和AC被直线BC所截而成;
∠1和∠BAE也是同旁内角,是直线DE和BC被直线AB所截而成;
∠2和∠EAC是内错角,是直线DE和BC被直线AC所截而成;
∠2和∠BAC是同旁内角,是直线AB和BC被直线AC所截而成;
∠2和∠1也是同旁内角,是直线AB和AC被直线BC所截而成;
∠2和∠DAC也是同旁内角,是直线DE和BC被直线AC所截而成.
17.【解析】
解:如图,可分解成三个基本图形,由图(1)得内错角:∠BAD和∠B;
由图(2)得同位角:∠DAE和∠C,同旁内角:∠CAD和∠C;
由图(3)得同位角:∠BAE和∠C,内错角:∠B和∠BAE,同旁内角:∠B和∠C,∠B和∠BAC,∠C和∠BAC.
即原图形中共有两组同位角,两组内错角,四组同旁内角.
18.【解析】
解:(1)∠C和∠D是同旁内角;
(2)∠B和∠GEF是同位角;
(3)∠A和∠D是内错角;
(4)∠AGE和∠BGE是邻补角;
(5)∠CFD和∠AFB是对顶角;
故答案为:(1)同旁内角 (2)同位角 (3)内错角 (4)邻补角 (5)对顶角
19.
20.【解析】∠1=∠2,与∠1互补的角有∠3和∠4.
理由:因为∠1=∠5,∠5=∠2,
所以∠1=∠2.
因为∠1=∠5,且∠5与∠3和∠4互补,
所以与∠1互补的角有∠3和∠4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版七年级下册数学5.1.1同位角、内错角、同旁内角
同步练习
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.如图,直线AD、BC被直线AC所截,则∠1和∠2是( ).
A.内错角 B.同位角 C.同旁内角 D.对顶角
2.如图,能与构成同位角的有( ).
A.4个 B.3个 C.2个 D.1个
3.下列命题中,真命题有( )
(1)直线外一点与直线上各点连接的所有线段中,垂线段最短;
(2)两条直线被第三条直线所截,内错角相等;
(3)经过两点有一条直线,并且只有一条直线;
(4)如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直.
A.1个 B.2个 C.3个 D.4个
4.若∠1与∠2是同位角,则它们之间的关系是( ).
A.∠1=∠2 ; B.∠1>∠2 ;
C.∠1<∠2; D.∠1=∠2或∠1>∠2或∠1<∠2.
5.如图所示,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
6.如图,以下说法正确的是
A.∠1和∠2是内错角 B.∠2和∠3是同位角
C.∠1和∠3是内错角 D.∠2和∠4是同旁内角
7.如图,下列说法错误的是
A.∠A与∠EDC是同位角 B.∠A与∠ABF是内错角
C.∠A与∠ADC是同旁内角 D.∠A与∠C是同旁内角
8.如图所示,∠1与∠2不是同位角的是
A. B.
C. D.
9.如图,属于内错角的是
A.∠1和∠2 B.∠2和∠3
C.∠1和∠4 D.∠3和∠4
10.∠1与∠2是直线a,b被直线c所截得的同位角,∠1与∠2的大小关系是
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
二、填空题(本大题共5小题,每小题4分,共20分。)
11.如图,当直线BC、DC被直线AB所截时,∠1的同位角是_______,同旁内角是_______;当直线AB、AC被直线BC所截时,∠1的同位角是________;当直线AB、BC被直线CD所截时,∠2的内错角是________.
12.如图,
(1)∠1和∠ABC是直线AB、CE被直线________所截得的________角;
(2)∠2和∠BAC是直线CE、AB被直线________所截得的________角;
(3)∠3和∠ABC是直线________、________被直线________所截得的________角;
(4)∠ABC和∠ACD是直线________、________被直线 所截得的________角;
(5)∠ABC和∠BCE是直线________、________被直线 所截得的________角.
13.如图,若∠1=95°,∠2=60°,则∠3的同位角等于________,∠3的内错角等于________,∠3的同旁内角等于________.
14.如图,如果∠2=100°,那么∠1的同位角等于__________,∠1的内错角等于__________,∠1的同旁内角等于__________.
15.如图,∠ABC与__________是同位角;∠ADB与__________是内错角;∠ABC与__________是同旁内角.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,∠1和哪些角是内错角 ∠1和哪些角是同旁内角 ∠2和哪些角是内错角 ∠2和哪些角是同旁内角 它们分别是由哪两条直线被哪一条线截成的
17.指出图中的同位角、内错角、同旁内角.
18.指出图中各对角的位置关系:
(1)∠C和∠D是 角;
(2)∠B和∠GEF是 角;
(3)∠A和∠D是 角;
(4)∠AGE和∠BGE是 角;
(5)∠CFD和∠AFB是 角.
19.如图:
(1)找出直线DC,AC被直线BE所截形成的同旁内角;
(2)指出∠DEF与∠CFE是由哪两条直线被哪一条直线所截形成的什么角;
(3)试找出图中与∠DAC是同位角的所有角.
20.如图所示,如果内错角∠1与∠5相等,那么与∠1相等的角还有吗?与∠1互补的角有吗?如果有,请写出来,并说明你的理由.
一、选择题
1. 【答案】A
【解析】∠1与∠2是直线AD、BC被直线AC所截而成,且这两角都在被截线AD、BC之间,在截线AC两侧,所以为内错角.
2.【答案】B
【解析】如图,与能构成同位角的有:∠1,∠2,∠3.
3. 【答案】B
【解析】(1)直线外一点与直线上各点连接的所有线段中,垂线段最短,正确;
(2)应为两条平行直线被第三条直线所截,内错角相等,故本选项错误;
(3)经过两点有一条直线,并且只有一条直线,正确;
(4)应为如果一条直线和两条平行直线中的一条垂直,那么这条直线也和另一条垂直,故本选项错误.
所以(1)(3)两项是真命题.
4. 【答案】D
【解析】由两角是同位角,内错角或同旁内角得不出它们大小之间的关系.
5. 【答案】A.
6.【答案】C
【解析】观察图形可得,∠1和∠2是同位角、∠2和∠3是对顶角、∠1和∠3是内错角、∠2和∠4是邻补角,所以正确的答案为C,故选C.
7.【答案】D
8.【答案】B
【解析】A中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
B中,∠1与∠2的两条边都不在同一条直线上,不是同位角,符合题意;
C中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
D中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意.
故选B.
9.【答案】D
10.【答案】D
【解析】因为不知道直线a、b之间的位置关系,所以∠1与∠2的大小关系无法确定.故选D.
填空题
11【答案】∠2, ∠5, ∠3, ∠4
【解析】先看哪两条线被哪一条线所截,再判断它们的关系.
12.【答案】(1)BD(或BC), 同位; (2)AC, 内错; (3)AB, AC, BC, 同旁内;
(4)AB, AC, BC,同位; (5)AB, CE, BC,同旁内.
【解析】可以从复杂图形中抽出简单图形进行分析.
13.【答案】85°, 85°, 95°
【解析】∠3的同位角和内错角均与∠1互补,故它们的度数均为:180°-95°=85°,
而∠3的同旁内角是∠1的对顶角,所以∠3的同旁内角的度数等于∠1的度数.
14.
【答案】80°,80°,100°
15.
【答案】∠EAD,∠DBC和∠EAD,∠DAB和∠BCD
【解析】根据同位角,内错角和同旁内角的概念进行判断,
(1) EMBED Equation.DSMT4 与是同位角;
(2)与是内错角;
(3)与是同旁内角.
故答案为:∠EAD,∠DBC和∠EAD,∠DAB和∠BCD.
三、解答题
16. 【解析】
解:∠1和∠DAB是内错角,由直线DE和BC被直线AB所截而成;
∠1和∠BAC是同旁内角,由直线BC和AC被直线AB所截而成;
∠1和∠2也是同旁内角,是直线AB和AC被直线BC所截而成;
∠1和∠BAE也是同旁内角,是直线DE和BC被直线AB所截而成;
∠2和∠EAC是内错角,是直线DE和BC被直线AC所截而成;
∠2和∠BAC是同旁内角,是直线AB和BC被直线AC所截而成;
∠2和∠1也是同旁内角,是直线AB和AC被直线BC所截而成;
∠2和∠DAC也是同旁内角,是直线DE和BC被直线AC所截而成.
17.【解析】
解:如图,可分解成三个基本图形,由图(1)得内错角:∠BAD和∠B;
由图(2)得同位角:∠DAE和∠C,同旁内角:∠CAD和∠C;
由图(3)得同位角:∠BAE和∠C,内错角:∠B和∠BAE,同旁内角:∠B和∠C,∠B和∠BAC,∠C和∠BAC.
即原图形中共有两组同位角,两组内错角,四组同旁内角.
18.【解析】
解:(1)∠C和∠D是同旁内角;
(2)∠B和∠GEF是同位角;
(3)∠A和∠D是内错角;
(4)∠AGE和∠BGE是邻补角;
(5)∠CFD和∠AFB是对顶角;
故答案为:(1)同旁内角 (2)同位角 (3)内错角 (4)邻补角 (5)对顶角
19.
20.【解析】∠1=∠2,与∠1互补的角有∠3和∠4.
理由:因为∠1=∠5,∠5=∠2,
所以∠1=∠2.
因为∠1=∠5,且∠5与∠3和∠4互补,
所以与∠1互补的角有∠3和∠4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
