平行四边行的性质(1)
图片预览





文档简介
课件24张PPT。19.1 平行四边形的性质(1)南门学校 八年(1)(2)班拼一拼 取出两张全等的三角形纸片拼平行四边形,你能拼出几种不同的平行四边形?观察:平行四边形相对的两边有怎样的位置关系?1、定义:
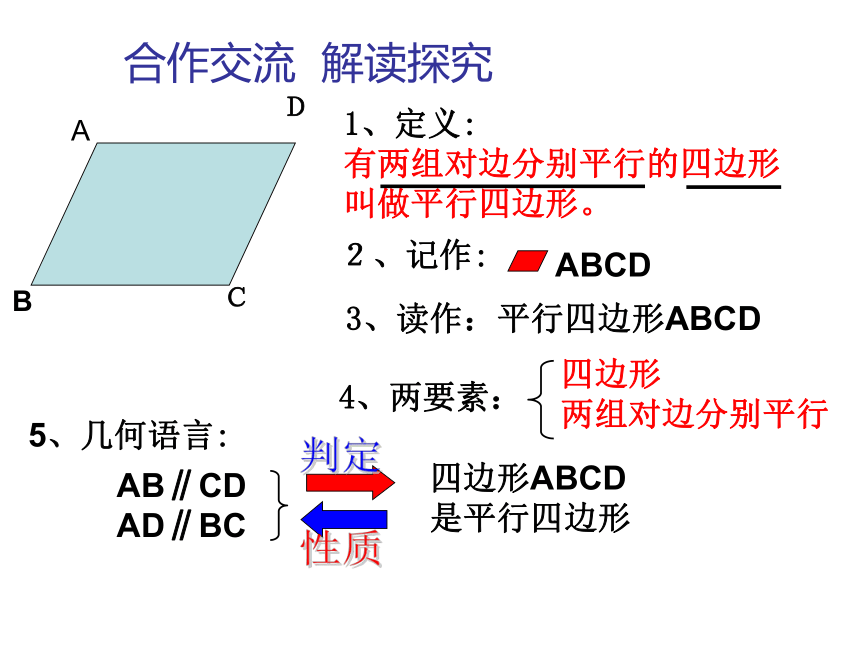
有两组对边分别平行的四边形 叫做平行四边形。2、记作:5、几何语言:
4、两要素: ABDC合作交流 解读探究四边形ABCD是平行四边形ABCD
AB∥CD AD∥BC3、读作:平行四边形ABCD性质判定ABCD1.平行四边形中
相对的边称为对边,
相对的角称为对角。2.平行四边形中相邻的边称为邻边,
相邻的角称为邻角。平行四边形的有关概念:3.平行四边形不相邻的两个顶点连成的
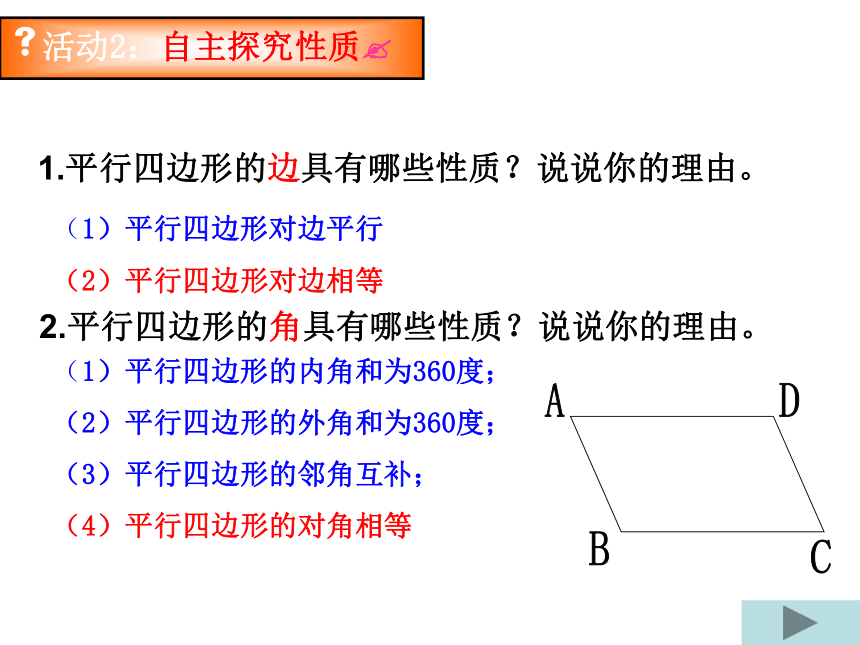
线段叫它的对角线。?活动2:自主探究性质? 1.平行四边形的边具有哪些性质?说说你的理由。2.平行四边形的角具有哪些性质?说说你的理由。(1)平行四边形对边平行
(2)平行四边形对边相等(1)平行四边形的内角和为360度;
(2)平行四边形的外角和为360度;
(3)平行四边形的邻角互补;
(4)平行四边形的对角相等即∠BAD=∠DCB证明:连结AC∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,AC=CA,∠3=∠4∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠3=∠2+∠4ABCD方法小结:有关四边形的问题常常
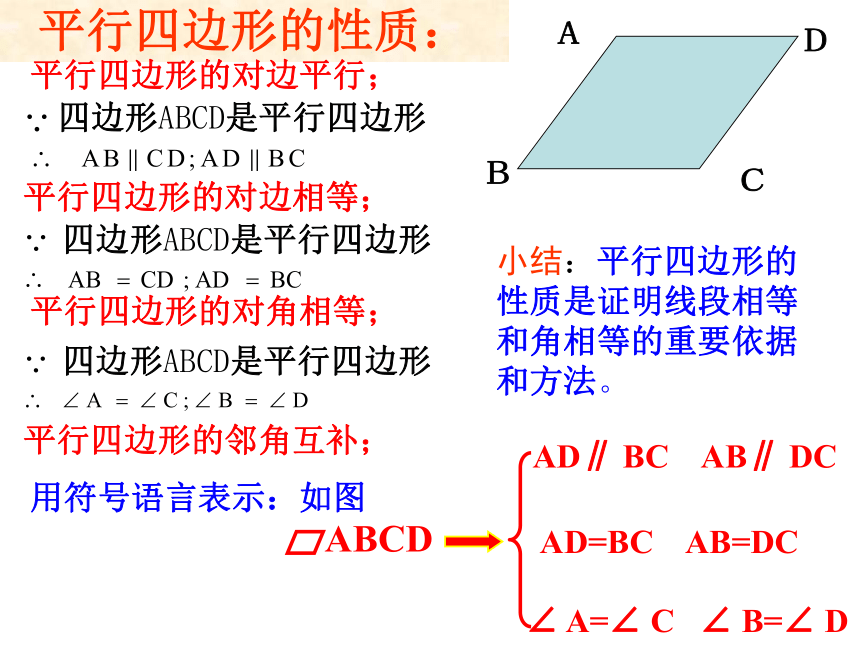
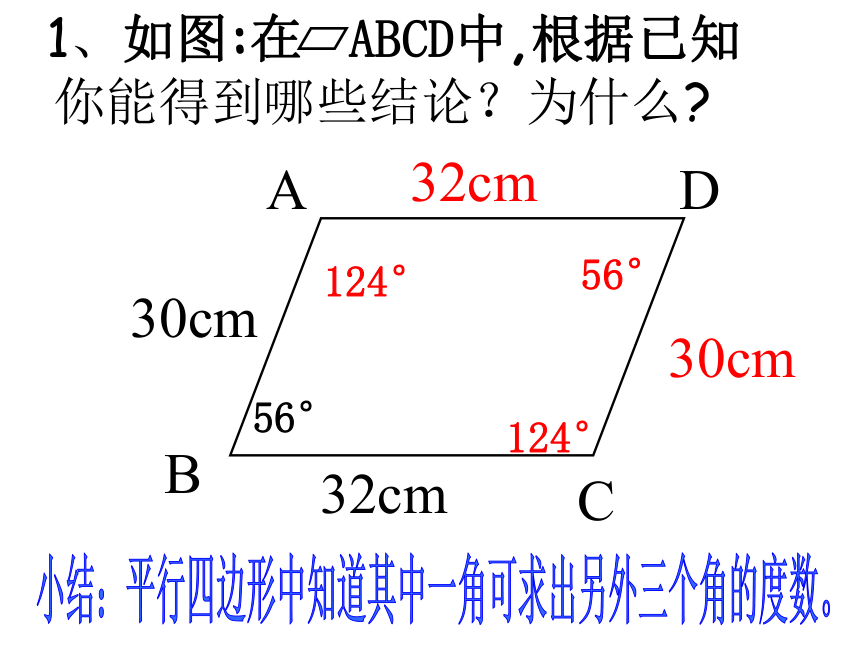
可转化为三角形问题来处理。平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;四边形ABCD是平行四边形四边形ABCD是平行四边形平行四边形的对边平行;四边形ABCD是平行四边形用符号语言表示:如图小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。32cm30cm56°124°124°小结:平行四边形中知道其中一角可求出另外三个角的度数。例2 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?∠A+∠C=200o,则∠A=?
∠B=?,∠C=?∠D=?ABCD解:ABCD∵四边形ABCD是平行四边形∴ AB=CD, AD=BC∵AB=3,又∵AB+BC+CD+AD=18解:例4:在平行四边形ABCD中,若周长为18cm,
且AB=3cm,求四边形其它三边的长?
3例5:如图,已知 ABCD中,AE⊥BD,CF⊥BD,垂足为E、F,
求证:EB=DF例6 如图,已知 ABCD中,∠A=1500,AB=8cm,BC=10cm,求四边形ABCD的面积。E 7.如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________。92. ABCD的周长为12cm,AD=xcm
BC= ;CD= .xcm (6-x)cm 4030120°120°60°等腰44.在 ABCD中,BE、DF为∠ABC与∠ADC的角平分线。说明: ②BF=DE①△AEB≌ △CFD5.已知如图, 在 ABCD中,
求证:①△ABE≌△CDF②AE=CFE、F分别是边BC和AD上的点,且BE=DF。ABCDEF小结:运用平行四边形的性质可证明线段、角相等或三角形全等。6.如图所示,△ABC中,AB=AC,点P是BC上任意一点,PE∥AC,PF∥AB,分别交AB、AC于E、F。
根据已知条件,你能得到哪些结论?线段PE,PF及其AB之间有何联系?并给予证明.
C 8.小明准备在自己书房的三角形透光窗ABC中加如图所示的横条,已知边AB=80cm,BC=100cm, 所加的横条平行于边AB或BC,请你利用所学的知识帮小明算一算加这些横条共需要多长木料?9.已知点A(3,0)、B(-1,0)、C(0,2),以A、B、C为顶点画平行四边形,你能求出第四个顶点D吗?(4,2)(2,-2)10.已知:如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,BE平分∠ABC交AD于E,交CD的延长线于F.
⑴△ABE与△DFE全等吗?⑵求CF的长.⑶若连结CE,则CE与BE有怎样的位置关系?⑷能否求出CE的长?勇攀高峰11如图, ABCD中,AB=8㎝,BC=6㎝,∠A=30°,点P从点A 出发沿AB以每秒1厘米的速度向点B移动。
(1)当P点运动了几秒时,△PBC为等腰三角形;
(2)设△PBC的面积为y,请写出y关于点P的运动时间t的函数关系式,并写出t的取值范围;
(3)是否存在一点P,使S△PBC= S ABCD?ABCDP8-tt6E)30°)30° 12.如图 在?ABC中,AD平分∠BAC,点M,E,F分别
是AB,AD,AC上的点,四边形BEFM是平行四边形
求证:AF=BM
BDCEFAM 证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BA
∴∠BAD=∠CAD
∵AB//EF
∴ ∠BAD=∠AEF
∴∠CAD =∠AEF
∴ AF=EF
∴ AF=BM练一练两组对边分别平行的四边形 ∵AB//CD, BC// AD,
∴四边形ABCD是平行四边形。 平行四边形的
对角相等,
对边相等,
对边平行,
AB = CD, AD = BC, AB//CD, AD//BC再 见
有两组对边分别平行的四边形 叫做平行四边形。2、记作:5、几何语言:
4、两要素: ABDC合作交流 解读探究四边形ABCD是平行四边形ABCD
AB∥CD AD∥BC3、读作:平行四边形ABCD性质判定ABCD1.平行四边形中
相对的边称为对边,
相对的角称为对角。2.平行四边形中相邻的边称为邻边,
相邻的角称为邻角。平行四边形的有关概念:3.平行四边形不相邻的两个顶点连成的
线段叫它的对角线。?活动2:自主探究性质? 1.平行四边形的边具有哪些性质?说说你的理由。2.平行四边形的角具有哪些性质?说说你的理由。(1)平行四边形对边平行
(2)平行四边形对边相等(1)平行四边形的内角和为360度;
(2)平行四边形的外角和为360度;
(3)平行四边形的邻角互补;
(4)平行四边形的对角相等即∠BAD=∠DCB证明:连结AC∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,AC=CA,∠3=∠4∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠3=∠2+∠4ABCD方法小结:有关四边形的问题常常
可转化为三角形问题来处理。平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;四边形ABCD是平行四边形四边形ABCD是平行四边形平行四边形的对边平行;四边形ABCD是平行四边形用符号语言表示:如图小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。32cm30cm56°124°124°小结:平行四边形中知道其中一角可求出另外三个角的度数。例2 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?∠A+∠C=200o,则∠A=?
∠B=?,∠C=?∠D=?ABCD解:ABCD∵四边形ABCD是平行四边形∴ AB=CD, AD=BC∵AB=3,又∵AB+BC+CD+AD=18解:例4:在平行四边形ABCD中,若周长为18cm,
且AB=3cm,求四边形其它三边的长?
3例5:如图,已知 ABCD中,AE⊥BD,CF⊥BD,垂足为E、F,
求证:EB=DF例6 如图,已知 ABCD中,∠A=1500,AB=8cm,BC=10cm,求四边形ABCD的面积。E 7.如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________。92. ABCD的周长为12cm,AD=xcm
BC= ;CD= .xcm (6-x)cm 4030120°120°60°等腰44.在 ABCD中,BE、DF为∠ABC与∠ADC的角平分线。说明: ②BF=DE①△AEB≌ △CFD5.已知如图, 在 ABCD中,
求证:①△ABE≌△CDF②AE=CFE、F分别是边BC和AD上的点,且BE=DF。ABCDEF小结:运用平行四边形的性质可证明线段、角相等或三角形全等。6.如图所示,△ABC中,AB=AC,点P是BC上任意一点,PE∥AC,PF∥AB,分别交AB、AC于E、F。
根据已知条件,你能得到哪些结论?线段PE,PF及其AB之间有何联系?并给予证明.
C 8.小明准备在自己书房的三角形透光窗ABC中加如图所示的横条,已知边AB=80cm,BC=100cm, 所加的横条平行于边AB或BC,请你利用所学的知识帮小明算一算加这些横条共需要多长木料?9.已知点A(3,0)、B(-1,0)、C(0,2),以A、B、C为顶点画平行四边形,你能求出第四个顶点D吗?(4,2)(2,-2)10.已知:如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,BE平分∠ABC交AD于E,交CD的延长线于F.
⑴△ABE与△DFE全等吗?⑵求CF的长.⑶若连结CE,则CE与BE有怎样的位置关系?⑷能否求出CE的长?勇攀高峰11如图, ABCD中,AB=8㎝,BC=6㎝,∠A=30°,点P从点A 出发沿AB以每秒1厘米的速度向点B移动。
(1)当P点运动了几秒时,△PBC为等腰三角形;
(2)设△PBC的面积为y,请写出y关于点P的运动时间t的函数关系式,并写出t的取值范围;
(3)是否存在一点P,使S△PBC= S ABCD?ABCDP8-tt6E)30°)30° 12.如图 在?ABC中,AD平分∠BAC,点M,E,F分别
是AB,AD,AC上的点,四边形BEFM是平行四边形
求证:AF=BM
BDCEFAM 证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BA
∴∠BAD=∠CAD
∵AB//EF
∴ ∠BAD=∠AEF
∴∠CAD =∠AEF
∴ AF=EF
∴ AF=BM练一练两组对边分别平行的四边形 ∵AB//CD, BC// AD,
∴四边形ABCD是平行四边形。 平行四边形的
对角相等,
对边相等,
对边平行,
AB = CD, AD = BC, AB//CD, AD//BC再 见
