16.1.2 二次根式的性质
图片预览










文档简介
(共32张PPT)
16.1 二次根式
第十六章 二次根式
第2课时 二次根式的性质
八年级数学下(RJ)教学课件
学习目标
1.理解二次根式的两个性质:
2.会用上述性质进行有关的计算和化简.
重点:理解二次根式的两个性质.
难点:利用性质进行计算和化简.
课前预习
阅读课本第3~4页内容,学习本节主要内容.
a
a
-a
新课导入
正方形的边长为 ,
用边长表示正方形的面积为 ,
又∵面积为a,
即 .
(a≥0)的性质
一
活动1 如图是一块具有民族风的正方形方巾,面积为a,求它的边长,并用所求得的边长表示出面积,你发现了什么?
这个式子是不是对所有的二次根式都成立呢?
新知讲解
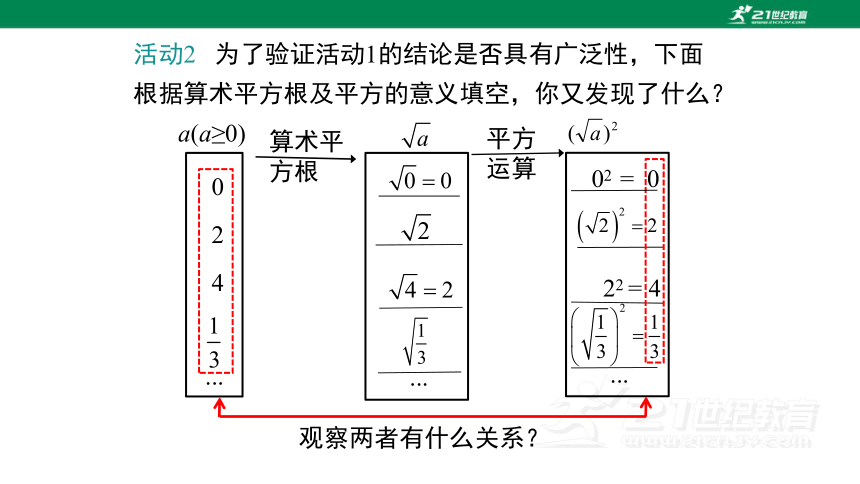
活动2 为了验证活动1的结论是否具有广泛性,下面根据算术平方根及平方的意义填空,你又发现了什么?
...
算术平方根
平方运算
0
2
4
...
a(a≥0)
02 = 0
...
观察两者有什么关系?
22 = 4
4
2
0
根据活动2直接写出结果,然后根据活动2的探究过程说明理由:
是2的算术平方根,根据算术平方根的意义,
是一个平方等于2的非负数.因此 .
同理, 分别是0,4, 的算术平方根,即得上面的等式.
归纳总结
的性质:
一般地, =a (a ≥0).
即一个非负数的算术平方根的平方等于它本身.
注意:不要忽略a≥0这一限制条件.这是使二次根式 有意义的前提条件.
例1 计算:
解:
(2)可以用到幂的哪条基本性质呢?
积的乘方:
(ab)2=a2b2
典例分析
例2 在实数范围内分解因式:
解:
本题逆用了 在实数范围内分解因式.在实数范围内分解因式时,原来在有理数范围内分解因式的方法和公式仍然适用.
归纳
练一练
计算:
解:
...
平方运算
算术平方根
2
0.1
0
...
a(a≥0)
2
...
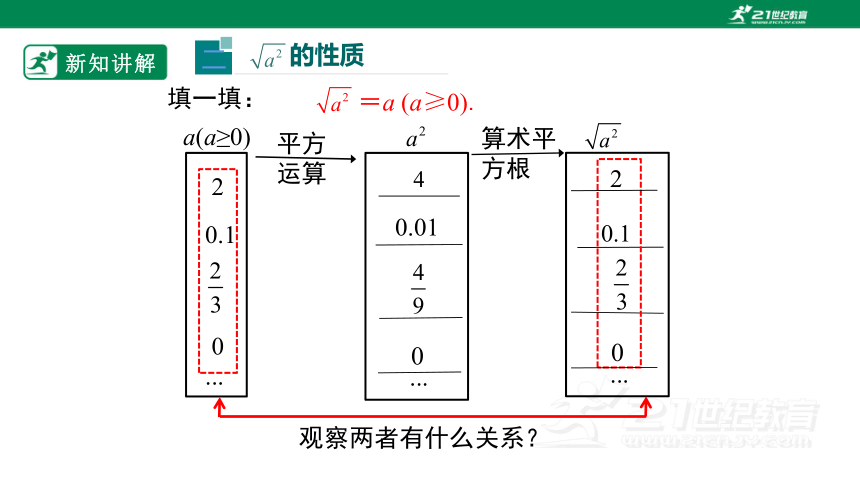
观察两者有什么关系?
的性质
二
填一填:
=a (a≥0).
新知讲解
...
平方运算
算术平方根
-2
-0.1
...
2
...
观察两者有什么关系?
a(a<0)
思考:当a<0时, =
?
-a
归纳总结
a (a≥0)
-a (a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值.
的性质:
例3 化简:
解:
,而3.14<π,要注意a的正负性.
注意
计算:
练一练
解:
辨一辨:请同学们快速分辨下列各题的对错.
( )
( )
( )
( )
×
×
√
√
议一议:如何区别 与 ?
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
例4 实数a、b在数轴上的对应点如图所示,请你化简:
解:由数轴可知a<0,b>0,a-b<0,
∴原式=|a|-|b|+|a-b|
=-a-b-(a-b)
=-2a.
a
b
【变式题】 实数a、b在数轴上的对应点如图所示,化简: .
解:根据数轴可知b<a<0,
∴a+2b<0,a-b>0,
则
=|a+2b|+|a-b|
=-a-2b+a-b=-3b.
利用数轴和二次根式的性质进行化简,关键是要要根据a,b的大小讨论绝对值内式子的符号.
注意
例5 已知a、b、c是△ABC的三边长,化简:
解:∵a、b、c是△ABC的三边长,
∴a+b>c,b+c>a,b+a>c,
∴原式=|a+b+c|-|b+c-a|+|c-b-a|
=a+b+c-(b+c-a)+(b+a-c)
=a+b+c-b-c+a+b+a-c
=3a+b-c.
分析:
利用三角形三边关系
三边长均为正数,a+b>c
两边之和大于第三边,b+c-a>0,c-b-a<0
用基本运算符号(包括加、减、乘、除、乘方和开方)把 或 连接起来的式子,我们称这样的式子为代数式.
概念学习
数
表示数的字母
想一想 到现在为止,初中阶段所学的代数式主要有哪几类?
代数式
整式
分式
二次根式
代数式的定义
三
新知讲解
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用代数式表示船在这条河中顺水行驶和逆水行驶时的速度;
例6
解:(1)船在这条河中顺水行驶的速度是 km/h,逆水行驶的速度是 km/h.
(2)如图,小语要制作一个长与宽之比为5:3的长方形贺卡,若面积为S,用代数式表示出它的长.
(2)设贺卡的长为5x,则宽为3x.依题意得15x2=S,所以 所以它的长为
列代数式的要点:
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
归纳总结
1.在下列各式中,不是代数式的是( )
A.7 B.3>2 C. D.
B
2.如图是一圆形挂钟,正面面积为S,用代数式表示出钟的半径为__________.
随堂练习
1.化简 得( )
A. ±4 B. ±2 C. 4 D.-4
C
2. 当1A.3 B.-3 C.1 D.-1
D
3.下列式子是代数式的有 ( )
①a2+b2 ; ② ; ③13; ④x=2; ⑤3×(4 -5);
⑥x-1≤0; ⑦10x+5y=15 ; ⑧
A.3个 B.4个 C.5个 D.6个
C
4.化简:
(1) = ; (2) = ;
(3) ; (4) .
3
7
4
81
-1
0
1
2
a
5. 实数a在数轴上的位置如图所示,化简
的结果是 .
1
6.利用a = (a≥0),把下列非负数分别写成一个非负数的平方的形式:
(1) 9 ; (2)5 ; (3) 2.5 ;
(4) 0.25 ; (5) ; (6)0 .
7.(1)已知a为实数,求代数式 的值.
解:由题意得a+2≥0,-4-2a≥0,
∴a=-2,
∴ .
(2)已知a为实数,求代数式 的值.
解:由题意得-a2≥0,又∵a2≥0,
∴a2=0,∴a=0,
∴
8. 已知 a、b、c 是△ABC 的三边长,化简:
分析:
| a + b + c| - | b + c - a | + | c - b - a |
上式
a + b + c - ( b + c - a ) + ( b + a - c)
3a + b - c
三角形三边关系:a + b + c>0
b + c - a>0,c - b - a<0
二次根式
性质
=a (a ≥0).
拓展性质
|a|(a为全体实数)
课堂小结
本课结束
*
*
16.1 二次根式
第十六章 二次根式
第2课时 二次根式的性质
八年级数学下(RJ)教学课件
学习目标
1.理解二次根式的两个性质:
2.会用上述性质进行有关的计算和化简.
重点:理解二次根式的两个性质.
难点:利用性质进行计算和化简.
课前预习
阅读课本第3~4页内容,学习本节主要内容.
a
a
-a
新课导入
正方形的边长为 ,
用边长表示正方形的面积为 ,
又∵面积为a,
即 .
(a≥0)的性质
一
活动1 如图是一块具有民族风的正方形方巾,面积为a,求它的边长,并用所求得的边长表示出面积,你发现了什么?
这个式子是不是对所有的二次根式都成立呢?
新知讲解
活动2 为了验证活动1的结论是否具有广泛性,下面根据算术平方根及平方的意义填空,你又发现了什么?
...
算术平方根
平方运算
0
2
4
...
a(a≥0)
02 = 0
...
观察两者有什么关系?
22 = 4
4
2
0
根据活动2直接写出结果,然后根据活动2的探究过程说明理由:
是2的算术平方根,根据算术平方根的意义,
是一个平方等于2的非负数.因此 .
同理, 分别是0,4, 的算术平方根,即得上面的等式.
归纳总结
的性质:
一般地, =a (a ≥0).
即一个非负数的算术平方根的平方等于它本身.
注意:不要忽略a≥0这一限制条件.这是使二次根式 有意义的前提条件.
例1 计算:
解:
(2)可以用到幂的哪条基本性质呢?
积的乘方:
(ab)2=a2b2
典例分析
例2 在实数范围内分解因式:
解:
本题逆用了 在实数范围内分解因式.在实数范围内分解因式时,原来在有理数范围内分解因式的方法和公式仍然适用.
归纳
练一练
计算:
解:
...
平方运算
算术平方根
2
0.1
0
...
a(a≥0)
2
...
观察两者有什么关系?
的性质
二
填一填:
=a (a≥0).
新知讲解
...
平方运算
算术平方根
-2
-0.1
...
2
...
观察两者有什么关系?
a(a<0)
思考:当a<0时, =
?
-a
归纳总结
a (a≥0)
-a (a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值.
的性质:
例3 化简:
解:
,而3.14<π,要注意a的正负性.
注意
计算:
练一练
解:
辨一辨:请同学们快速分辨下列各题的对错.
( )
( )
( )
( )
×
×
√
√
议一议:如何区别 与 ?
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
例4 实数a、b在数轴上的对应点如图所示,请你化简:
解:由数轴可知a<0,b>0,a-b<0,
∴原式=|a|-|b|+|a-b|
=-a-b-(a-b)
=-2a.
a
b
【变式题】 实数a、b在数轴上的对应点如图所示,化简: .
解:根据数轴可知b<a<0,
∴a+2b<0,a-b>0,
则
=|a+2b|+|a-b|
=-a-2b+a-b=-3b.
利用数轴和二次根式的性质进行化简,关键是要要根据a,b的大小讨论绝对值内式子的符号.
注意
例5 已知a、b、c是△ABC的三边长,化简:
解:∵a、b、c是△ABC的三边长,
∴a+b>c,b+c>a,b+a>c,
∴原式=|a+b+c|-|b+c-a|+|c-b-a|
=a+b+c-(b+c-a)+(b+a-c)
=a+b+c-b-c+a+b+a-c
=3a+b-c.
分析:
利用三角形三边关系
三边长均为正数,a+b>c
两边之和大于第三边,b+c-a>0,c-b-a<0
用基本运算符号(包括加、减、乘、除、乘方和开方)把 或 连接起来的式子,我们称这样的式子为代数式.
概念学习
数
表示数的字母
想一想 到现在为止,初中阶段所学的代数式主要有哪几类?
代数式
整式
分式
二次根式
代数式的定义
三
新知讲解
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用代数式表示船在这条河中顺水行驶和逆水行驶时的速度;
例6
解:(1)船在这条河中顺水行驶的速度是 km/h,逆水行驶的速度是 km/h.
(2)如图,小语要制作一个长与宽之比为5:3的长方形贺卡,若面积为S,用代数式表示出它的长.
(2)设贺卡的长为5x,则宽为3x.依题意得15x2=S,所以 所以它的长为
列代数式的要点:
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
归纳总结
1.在下列各式中,不是代数式的是( )
A.7 B.3>2 C. D.
B
2.如图是一圆形挂钟,正面面积为S,用代数式表示出钟的半径为__________.
随堂练习
1.化简 得( )
A. ±4 B. ±2 C. 4 D.-4
C
2. 当1
D
3.下列式子是代数式的有 ( )
①a2+b2 ; ② ; ③13; ④x=2; ⑤3×(4 -5);
⑥x-1≤0; ⑦10x+5y=15 ; ⑧
A.3个 B.4个 C.5个 D.6个
C
4.化简:
(1) = ; (2) = ;
(3) ; (4) .
3
7
4
81
-1
0
1
2
a
5. 实数a在数轴上的位置如图所示,化简
的结果是 .
1
6.利用a = (a≥0),把下列非负数分别写成一个非负数的平方的形式:
(1) 9 ; (2)5 ; (3) 2.5 ;
(4) 0.25 ; (5) ; (6)0 .
7.(1)已知a为实数,求代数式 的值.
解:由题意得a+2≥0,-4-2a≥0,
∴a=-2,
∴ .
(2)已知a为实数,求代数式 的值.
解:由题意得-a2≥0,又∵a2≥0,
∴a2=0,∴a=0,
∴
8. 已知 a、b、c 是△ABC 的三边长,化简:
分析:
| a + b + c| - | b + c - a | + | c - b - a |
上式
a + b + c - ( b + c - a ) + ( b + a - c)
3a + b - c
三角形三边关系:a + b + c>0
b + c - a>0,c - b - a<0
二次根式
性质
=a (a ≥0).
拓展性质
|a|(a为全体实数)
课堂小结
本课结束
*
*
