2023-2024学年数学七年级二元一次方程组单元测试试题(鲁教版(五四制))提升卷一含解析
文档属性
| 名称 | 2023-2024学年数学七年级二元一次方程组单元测试试题(鲁教版(五四制))提升卷一含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 992.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 19:36:48 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学七年级二元一次方程组(鲁教版(五四制))单元测试 提升卷一 含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题,译文为:现有几个人共同购买一个物品,每人出8元,则多3元;每人出7元,则差4元.问这个物品的价格是多少元?有多少人共同购买?设这个物品的价格是元,有人共同购买,则可列出的方程组为( )
A. B. C. D.
2.(本题3分)一次函数与的图象如图所示,则关于x,y的方程组的解是( )
A. B. C. D.
3.(本题3分)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”意思是:笼子里有鸡和兔若干只,共有个头,共有只足,问笼子里鸡和兔各有多少只?设鸡有只,兔有只,下列方程组正确的是()
A. B.
C. D.
4.(本题3分)已知直线与直线相交于点,则关于x,y的方程组的解是( )
A. B. C. D.
5.(本题3分)我国古典数学文献《增删算法统宗 六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详.甲云得乙九只羊,多乙一倍之上,乙说得甲九只,两家之数相当,二人闲坐恼心肠,画地算了半晌”其大意为:甲,乙两人一起放牧,两人心里暗中数羊.如果乙给甲9只羊,那么甲的羊数为乙的2倍;如果甲给乙9只羊,那么两人的羊数相同.请问甲,乙各有多少只羊?设甲有羊x只,乙有羊y只,根据题意列方程组正确的为( )
A. B.
C. D.
6.(本题3分)在同一平面直角坐标系中,函数 和 交于点 ,则点 的纵坐标为( )
A.2 B. C. D.
7.(本题3分)已知多项式中,,,为常数,的取值与多项式对应的值如下表:
1 2
7
则值为( )
A.15 B.19 C.21 D.23
8.(本题3分)《九章算术》是中国古代第一部数学专著,在其方程章中有一道题:“今有甲、乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而亦钱五十.甲、乙持钱几何?”.题意大意是:甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半,那么甲共有钱.如果乙得到甲所有钱的,那么乙也共有钱.甲、乙两人各带了多少钱?若设甲带钱为,乙带钱为,则可列方程组( )
A. B.
C. D.
9.(本题3分)把方程改写成含x的式子表示y的形式为( )
A. B. C. D.
10.(本题3分)正比例函数(为整数)与直线的交点坐标恰好是格点(横、纵坐标都是整数的点称为格点),那么满足条件的正比例函数有( ).
A.个 B.个 C.个 D.无数个
评卷人得分
二、填空题(共24分)
11.(本题3分)定义运算“*”,规定,其中为常数,且,,则 .
12.(本题3分)若方程组的解是,则直线与交点的坐标为 .
13.(本题3分)如图,直线与直线相交于点,则关于,的方程组的解是 .
14.(本题3分)如图,在同一直角坐标系中,直线与直线相交于点,则方程组的解为 .
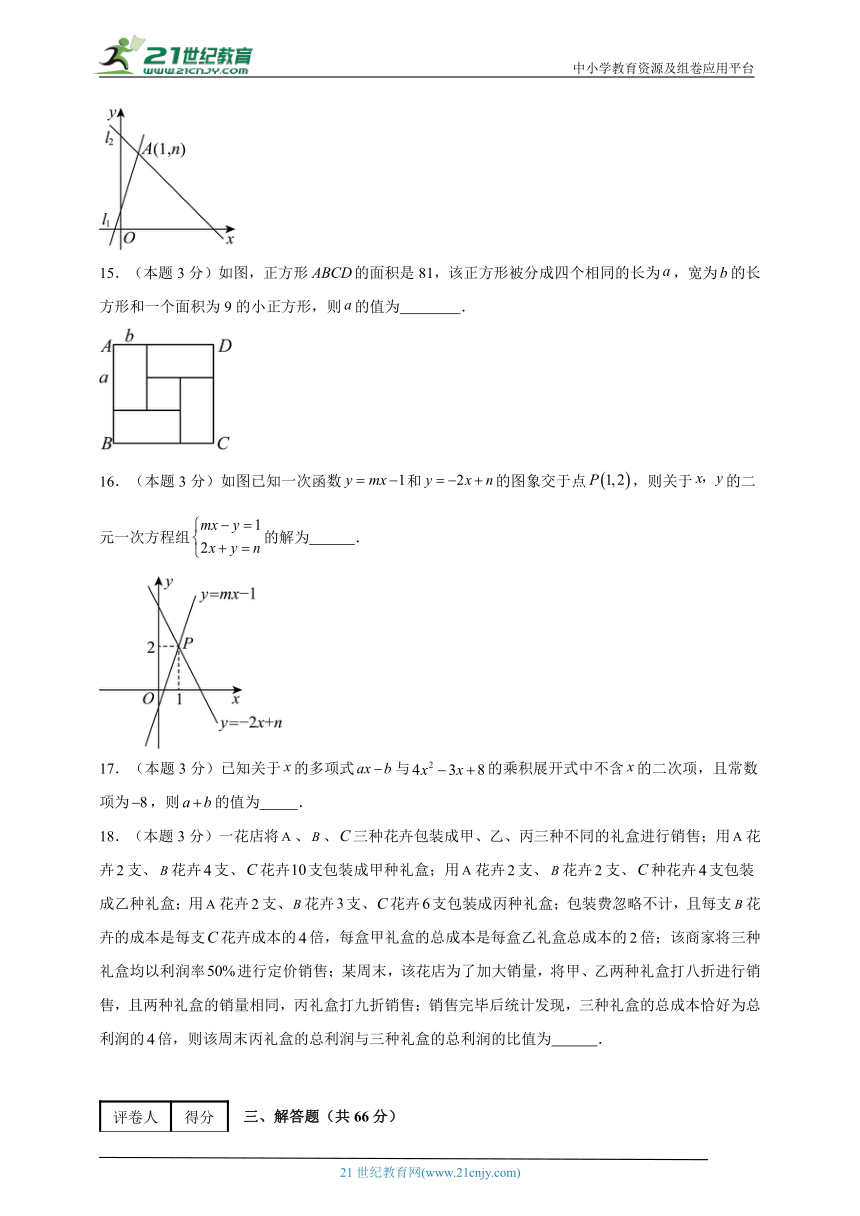
15.(本题3分)如图,正方形的面积是81,该正方形被分成四个相同的长为,宽为的长方形和一个面积为9的小正方形,则的值为 .
16.(本题3分)如图已知一次函数和的图象交于点,则关于的二元一次方程组的解为 .
17.(本题3分)已知关于的多项式与的乘积展开式中不含的二次项,且常数项为,则的值为 .
18.(本题3分)一花店将、、三种花卉包装成甲、乙、丙三种不同的礼盒进行销售;用花卉支、花卉支、花卉支包装成甲种礼盒;用花卉支、花卉支、种花卉支包装成乙种礼盒;用花卉支、花卉支、花卉支包装成丙种礼盒;包装费忽略不计,且每支花卉的成本是每支花卉成本的倍,每盒甲礼盒的总成本是每盒乙礼盒总成本的倍;该商家将三种礼盒均以利润率进行定价销售;某周末,该花店为了加大销量,将甲、乙两种礼盒打八折进行销售,且两种礼盒的销量相同,丙礼盒打九折销售;销售完毕后统计发现,三种礼盒的总成本恰好为总利润的倍,则该周末丙礼盒的总利润与三种礼盒的总利润的比值为 .
评卷人得分
三、解答题(共66分)
19.(本题8分)解方程组:
(1); (2).
20.(本题8分)已知,
(1)求的值;
(2)求和的值.
21.(本题10分)某水果零售商店在水蜜桃销售季节分两批次从批发市场共购进水蜜桃80箱,已知第一、二次进货价分别为每箱60元、50元,且第二次比第一次多付款700元.
(1)求第一、二次各购进水蜜桃多少箱;
(2)若商店对这80箱水蜜桃先按每箱80元销售了45箱,其余的每箱打八折销售,求该商店销售完全部水蜜桃所获得的利润.(注:按整箱出售,利润﹣销售总收入﹣进货总成本)
22.(本题10分)用5张大小完全相同的长方形纸片在平面直角坐标系中摆成如图图案,已知点的坐标为,求点的坐标.
23.(本题10分)某校开设智能机器人编程的校本课程,购买了A,B两种型号的机器人模型.已知A型机器人模型单价比B型机器人模型单价多200元,购买5台A型机器人模型的费用比购买7台B型机器人模型的费用多400元.
(1)求A型,B型机器人模型的单价分别是多少元?
(2)现在需要购买A型号机器人模型5台,B型号机器人模型7台,求共需要花费多少钱?
24.(本题10分)某中学为了在11月中旬举办体育文化节,学校委托后勤处张主任去购买奖品,张主任回校后向财务处的陈老师交账说:“我买了足球和篮球共20个,足球每个60元,篮球每个80元,去买之前我领了1500元,现在还余70元.”陈老师算了一下,说:“你肯定搞错了.”
(1)陈老师为什么说张主任肯定搞错了?试用方程的知识给予解释.
(2)张主任连忙拿出购物发票,发现的确弄错了,因为他还买了几个(大于1小于4)单价为15元的水龙头,但是发票上的个数看不清了,请你帮他算一算,他买了几个水龙头?
25.(本题10分)如图,直线与轴交于点,与轴交于点.直线与直线交于点,与轴交于点.
(1)求的值及点的坐标.
(2)求的面积.
(3)连接,在轴上有一点,使得的面积等于面积的.直接写出此时点的坐标.
参考答案:
1.B
【分析】本题主要考查了从实际问题中抽象出二元一次方程组,设这个物品的价格是元,有人共同购买,根据每人出8元,则多3元可得方程,根据每人出7元,则差4元可得方程,据此列出方程组即可.
【详解】解:设这个物品的价格是元,有人共同购买,
由题意得,,
故选:B.
2.A
【分析】本题考查了一次函数与二元一次方程(组):方程组的解就是两个相应的一次函数图象的交点坐标.先利用确定交点坐标,然后根据方程组的解就是两个相应的一次函数图象的交点坐标进行判断.
【详解】解:对于,当时,,
∴两直线交点坐标为,
∴方程组的解,
故选:A.
3.C
【分析】本题主要考查由实际问题抽象出二元一次方程组,解题的关键是理解题意,找到题目的等量关系.根据“鸡的数量兔的数量,鸡的脚的数量兔子的脚的数量”可列方程组.
【详解】解:设鸡有只,兔有只,
根据题意,可列方程组为,
故选:C.
4.A
【分析】此题主要考查了二元一次方程组与一次函数的关系,关键是掌握两函数图象的交点坐标就是两函数解析式组成的二元一次方程组的解.根据二元一次方程组的解的定义知,该方程组的解就是组成方程组的两个二元一次方程的图象的交点坐标.
【详解】解:直线与直线相交于点,
关于,的方程组的解为.
故选:A.
5.D
【分析】根据“如果乙给甲9只羊,那么甲的羊数为乙的2倍;如果甲给乙9只羊,那么两人的羊数相同”,列出二元一次方程组,即可求解,本题考查了二元一次方程组的实际应用,解题的关键是:正确理解题意,列出等量关系.
【详解】解:由“如果乙给甲9只羊,那么甲的羊数为乙的2倍,”可列式:,
由“如果甲给乙9只羊,那么两人的羊数相同,”可列式:,
根据题意可列二元一次方程组:,
故选:.
6.A
【分析】本题考查两条直线的交点问题,先联立方程组,然后两式相加消去,即可求出y,从而得解,掌握求两直线交点的方法是解题的关键.
【详解】解:联立方程组得:,
得:,
解得:,
即点A的纵坐标为2,
故选:A.
7.D
【分析】本题考查的是三元一次方程组的特殊解法,先根据表格信息建立方程组,再利用整体未知数的方法解方程即可;先求解,,再利用整体代入法可得答案.
【详解】解:当时,①,
当时,②,
当时,③,
当时,④,
③①得:,即,
④②得:,
∴,
∴,
∴;
故选D
8.A
【分析】本题考查了二元一次方程组的应用,设甲带钱为,乙带钱为,根据题意列出方程组即可求解,根据题意,找到等量关系,列出方程组是解题的关键.
【详解】解:设甲带钱为,乙带钱为,
由题意可得,
故选:.
9.B
【分析】本题考查了二元一次方程的变形,把x看作已知数求出y即可.
【详解】解:,
,
,
故选:B.
10.C
【分析】本题考查了一次函数与二元一次方程组之间的关系,联立函数式得方程组,由方程组得,根据点坐标恰好是格点,即可得到,解之即可求解,解题的关键是根据题意,联立方程组,对方程组的解进行分析.
【详解】解:由得,,
为整数,
,
,
又,
满足条件的有个,正比例函数解析式也有个,
故选:.
11.17
【分析】本题考查了解二元一次方程组和有理数的混合运算,得出关于a、b的方程组是解题的关键.
根据已知定义得出方程,,整理后得出关于a、b的方程组,求出a、b的值,再根据定义得出算式,最后求出答案即可.
【详解】解:根据题中的新定义化简已知等式,得,解得,
所以,
则.
故答案为:17.
12./
【分析】本题考查了一次函数与二元一次方程组.二元一次方程可以化为一次函数,两个二元一次方程组的解就是两个函数的交点坐标.
【详解】解:∵方程组的解是,
∴直线与的交点坐标是.
故答案为:.
13./
【分析】本题主要考查了一次函数与二元一次方程组之间的关系,先求出,再由两直线的交点的横纵坐标即为两直线解析式对应的二元一次方程组的解可得答案.
【详解】解:在中,当时,则,解得,
∴,
∵直线与直线相交于点,
∴关于,的方程组的解是,
故答案为:.
14.
【分析】此题主要考查了一次函数与二元一次方程组的关系,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数解析式,因此方程组的解就是两个相应的一次函数图象的交点坐标.把代入求出值可得出点坐标,即可得答案.
【详解】解:∵直线与直线相交于点,
∴,
∴,
∴方程组的解为.
故答案为:
15.6
【分析】本题考查了二元一次方程的应用,根据正方形的面积为81,可得正方形的边长为9,即,可列出一个关于a、b的方程,解方程组即可.
【详解】解:根据正方形的面积为81,可得正方形的边长为9,即,
小正方形的面积为9,则其边长为3,
∵大正方形边长为9,小正方形边长为3,
∴根据图示和题意得:,
解得:.
故答案为:6.
16.
【分析】本题考查了一次函数的交点与二元一次方程组解的关系,根据:一次函数的交点坐标就是以一次函数解析式所构成的二元一次方程组的解,即可求解,掌握一次函数的交点与二元一次方程组解的关系是解题的关键.
【详解】解:∵一次函数和的图象交于点,
∴关于的二元一次方程组的解为,
故答案为:.
17.
【分析】本题考查多项式乘以多项式,二元一次方程组的应用,代数式求值,解题的关键是明确不含的二次项,则二次项的系数为0.先利用多项式乘以多项式展开,进而得出二元一次方程组,求出、的值,代入计算即可.
【详解】解:
,
多项式与的乘积展开式中不含的二次项,且常数项为,
,
,
故.
故答案为:.
18.
【分析】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
设每支花卉成本是元,每支花卉成本是元,则每支花卉成本是元,根据每盒甲礼盒的总成本是每盒乙礼盒总成本的倍,可列出关于,的二元一次方程,解之可得出,继而可用含的代数式表示出每盒甲、乙、丙种礼盒的总成本,设该周末花店售出盒甲种礼盒,盒丙种礼盒,则售出盒乙种礼盒,根据三种礼盒的总成本恰好为总利润的倍,可列出关于,的二元一次方程,解之可得出,再用含,的代数式表示出该周末丙礼盒的总利润及三种礼盒的总利润,作比后即可得出结论.
【详解】解:设每支花卉成本是元,每支花卉成本是元,则每支花卉成本是元,
根据题意得:,
,
每盒甲种礼盒的总成本为:(元);
每盒乙种礼盒的总成本为:(元);
每盒丙种礼盒的总成本为:(元).
设该周末花店售出盒甲种礼盒,盒丙种礼盒,则售出盒乙种礼盒,
根据题意得:,
,
∴,
该周末丙礼盒的总利润为:(元),
三种礼盒的总利润为:(元),
该周末丙礼盒的总利润与三种礼盒的总利润的比值为:,
故答案为:.
19.(1)
(2)
【分析】本题考查了二元一次方程组的求解,掌握消元法是解题关键.
(1)利用代入消元法即可求解;
(2)综合利用代入消元法和加减消元法即可求解;
【详解】(1)解:
得:,
将①代入③得:,
解得:
将代入①得:
∴原方程组的解为:
(2)解:
得:
解得:
将代入①得:,
解得:
∴原方程组的解为:
20.(1)
(2)
【分析】此题考查了平方差公式,以及解二元一次方程组;熟练掌握公式及法则是解本题的关键.
(1)已知第二个等式左边利用平方差公式化简,把第一个等式代入求出的值即可;
(2)联立求出与的值即可.
【详解】(1)解:,,
,
;
(2)解:联立得:,
①+②得:,
解得:,
将代入②得
,
.
21.(1)第一、二次各购进水蜜桃30和50箱;
(2)利润为1540元
【分析】本题考查的是二元一次方程的应用,混合运算的实际应用,理解题意确定相等关系是解本题的关键;
(1)设第一、二次各购进水蜜桃a箱和b箱,利用“共购进水蜜桃80箱,已知第一、二次进货价分别为每箱60元、50元,且第二次比第一次多付款700元”,再建立方程求解即可;
(2)把打折前与打折后的利润相加即可.
【详解】(1)解:设第一、二次各购进水蜜桃a箱和b箱,由题意可得,
,
解得,,
答:第一、二次各购进水蜜桃30和50箱;
(2)该商店销售完全部水蜜桃所获得的利润为:
(元),
答:利润为1540元.
22.
【分析】本题主要考查了坐标与图形、二元一次方程组的应用等知识,正确列出二元一次方程并求解是解题关键.设小长方形的长为,宽为,根据题意列出二元一次方程组并求解,然后确定点的坐标即可.
【详解】解:设小长方形的长为,宽为,
依题意,得,
解得,
∴,,
∴点的坐标为.
23.(1)A型机器人模型的单价为500元,B型机器人模型的单价为300元
(2)一共需要4600元
【分析】本题主要考查了二元一次方程组的实际应用,有理数四则混合计算的实际应用:
(1)设A型机器人模型的单价为x元,B型机器人模型的单价为y元,根据A型机器人模型单价比B型机器人模型单价多200元,购买5台A型机器人模型的费用比购买7台B型机器人模型的费用多400元列出方程组求解即可;
(2)根据(1)所求分别求出两种机器人的费用,然后求和即可得到答案.
【详解】(1)解:设A型机器人模型的单价为x元,B型机器人模型的单价为y元.
由题意得,,
解得:,
答:A型机器人模型的单价为500元,B型机器人模型的单价为300元.
(2)解:元
答:一共需要4600元.
24.(1)张主任肯定搞错了,理由见解析
(2)2个水龙头
【分析】本题考查二元一次方程(组)的应用:
(1)设足球买了个,篮球买了个.根据题意列二元一次方程组,根据方程组的解是否为正整数即可解释;
(2)设张主任买了个足球,个水龙头,根据题意列二元一次方程,由,都是整数,且,确定n可能的取值,进而求出m的值,判断是否符合题意即可.
【详解】(1)解:设足球买了个,篮球买了个.
依题意,得,
解得,
,均为正整数,
不符合题意,即张主任肯定搞错了.
(2)解:设张主任买了个足球,个水龙头,则买的篮球的个数为个.
依题意,得,
整理,得.
,都是整数,且,
可能为2或3.
当时,,解得,符合题意;
当时,,解得,不符合题意,
他买了2个水龙头.
25.(1)
(2)
(3)或
【分析】(1)根据直线与x轴的交点可求得b的值,进而得到解析式,即可求得点的坐标;
(2)根据两个直线的解析式联立求得交点坐标D,以及点C的坐标,的面积以为底,以点D的横坐标的绝对值为高,即可求得面积;
(3)先求出的面积,根据两个三角形面积之间的关系求得面积,然后设出的长,根据面积分割法列得等式,求解即可,注意分情况讨论.
【详解】(1)解:∵直线与轴交于点,
∴,
解得:,
∴直线,
令,解得,
∴;
(2)解:∵直线与直线交于点,
∴,解得,
∴,
∵直线与轴交于点,
∴令,解得,
∴,
即,
∴;
(3)解:由(1)(2)可得,,,
∴,
∵的面积等于面积的,
∴,
设,
则,
即,
解得:,
∵,点在轴上,
当点E在点A左侧时,点E的横坐标为:,此时点,
当点E在点A右侧时,点E的横坐标为:,此时点,
∴点E的坐标为或.
【点睛】本题考查了直线围成的三角形的面积,待定系数法求一次函数的解析式,一次函数图像上点的坐标特征,分割法求三角形的面积,运用数形结合是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学七年级二元一次方程组(鲁教版(五四制))单元测试 提升卷一 含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题,译文为:现有几个人共同购买一个物品,每人出8元,则多3元;每人出7元,则差4元.问这个物品的价格是多少元?有多少人共同购买?设这个物品的价格是元,有人共同购买,则可列出的方程组为( )
A. B. C. D.
2.(本题3分)一次函数与的图象如图所示,则关于x,y的方程组的解是( )
A. B. C. D.
3.(本题3分)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”意思是:笼子里有鸡和兔若干只,共有个头,共有只足,问笼子里鸡和兔各有多少只?设鸡有只,兔有只,下列方程组正确的是()
A. B.
C. D.
4.(本题3分)已知直线与直线相交于点,则关于x,y的方程组的解是( )
A. B. C. D.
5.(本题3分)我国古典数学文献《增删算法统宗 六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详.甲云得乙九只羊,多乙一倍之上,乙说得甲九只,两家之数相当,二人闲坐恼心肠,画地算了半晌”其大意为:甲,乙两人一起放牧,两人心里暗中数羊.如果乙给甲9只羊,那么甲的羊数为乙的2倍;如果甲给乙9只羊,那么两人的羊数相同.请问甲,乙各有多少只羊?设甲有羊x只,乙有羊y只,根据题意列方程组正确的为( )
A. B.
C. D.
6.(本题3分)在同一平面直角坐标系中,函数 和 交于点 ,则点 的纵坐标为( )
A.2 B. C. D.
7.(本题3分)已知多项式中,,,为常数,的取值与多项式对应的值如下表:
1 2
7
则值为( )
A.15 B.19 C.21 D.23
8.(本题3分)《九章算术》是中国古代第一部数学专著,在其方程章中有一道题:“今有甲、乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而亦钱五十.甲、乙持钱几何?”.题意大意是:甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半,那么甲共有钱.如果乙得到甲所有钱的,那么乙也共有钱.甲、乙两人各带了多少钱?若设甲带钱为,乙带钱为,则可列方程组( )
A. B.
C. D.
9.(本题3分)把方程改写成含x的式子表示y的形式为( )
A. B. C. D.
10.(本题3分)正比例函数(为整数)与直线的交点坐标恰好是格点(横、纵坐标都是整数的点称为格点),那么满足条件的正比例函数有( ).
A.个 B.个 C.个 D.无数个
评卷人得分
二、填空题(共24分)
11.(本题3分)定义运算“*”,规定,其中为常数,且,,则 .
12.(本题3分)若方程组的解是,则直线与交点的坐标为 .
13.(本题3分)如图,直线与直线相交于点,则关于,的方程组的解是 .
14.(本题3分)如图,在同一直角坐标系中,直线与直线相交于点,则方程组的解为 .
15.(本题3分)如图,正方形的面积是81,该正方形被分成四个相同的长为,宽为的长方形和一个面积为9的小正方形,则的值为 .
16.(本题3分)如图已知一次函数和的图象交于点,则关于的二元一次方程组的解为 .
17.(本题3分)已知关于的多项式与的乘积展开式中不含的二次项,且常数项为,则的值为 .
18.(本题3分)一花店将、、三种花卉包装成甲、乙、丙三种不同的礼盒进行销售;用花卉支、花卉支、花卉支包装成甲种礼盒;用花卉支、花卉支、种花卉支包装成乙种礼盒;用花卉支、花卉支、花卉支包装成丙种礼盒;包装费忽略不计,且每支花卉的成本是每支花卉成本的倍,每盒甲礼盒的总成本是每盒乙礼盒总成本的倍;该商家将三种礼盒均以利润率进行定价销售;某周末,该花店为了加大销量,将甲、乙两种礼盒打八折进行销售,且两种礼盒的销量相同,丙礼盒打九折销售;销售完毕后统计发现,三种礼盒的总成本恰好为总利润的倍,则该周末丙礼盒的总利润与三种礼盒的总利润的比值为 .
评卷人得分
三、解答题(共66分)
19.(本题8分)解方程组:
(1); (2).
20.(本题8分)已知,
(1)求的值;
(2)求和的值.
21.(本题10分)某水果零售商店在水蜜桃销售季节分两批次从批发市场共购进水蜜桃80箱,已知第一、二次进货价分别为每箱60元、50元,且第二次比第一次多付款700元.
(1)求第一、二次各购进水蜜桃多少箱;
(2)若商店对这80箱水蜜桃先按每箱80元销售了45箱,其余的每箱打八折销售,求该商店销售完全部水蜜桃所获得的利润.(注:按整箱出售,利润﹣销售总收入﹣进货总成本)
22.(本题10分)用5张大小完全相同的长方形纸片在平面直角坐标系中摆成如图图案,已知点的坐标为,求点的坐标.
23.(本题10分)某校开设智能机器人编程的校本课程,购买了A,B两种型号的机器人模型.已知A型机器人模型单价比B型机器人模型单价多200元,购买5台A型机器人模型的费用比购买7台B型机器人模型的费用多400元.
(1)求A型,B型机器人模型的单价分别是多少元?
(2)现在需要购买A型号机器人模型5台,B型号机器人模型7台,求共需要花费多少钱?
24.(本题10分)某中学为了在11月中旬举办体育文化节,学校委托后勤处张主任去购买奖品,张主任回校后向财务处的陈老师交账说:“我买了足球和篮球共20个,足球每个60元,篮球每个80元,去买之前我领了1500元,现在还余70元.”陈老师算了一下,说:“你肯定搞错了.”
(1)陈老师为什么说张主任肯定搞错了?试用方程的知识给予解释.
(2)张主任连忙拿出购物发票,发现的确弄错了,因为他还买了几个(大于1小于4)单价为15元的水龙头,但是发票上的个数看不清了,请你帮他算一算,他买了几个水龙头?
25.(本题10分)如图,直线与轴交于点,与轴交于点.直线与直线交于点,与轴交于点.
(1)求的值及点的坐标.
(2)求的面积.
(3)连接,在轴上有一点,使得的面积等于面积的.直接写出此时点的坐标.
参考答案:
1.B
【分析】本题主要考查了从实际问题中抽象出二元一次方程组,设这个物品的价格是元,有人共同购买,根据每人出8元,则多3元可得方程,根据每人出7元,则差4元可得方程,据此列出方程组即可.
【详解】解:设这个物品的价格是元,有人共同购买,
由题意得,,
故选:B.
2.A
【分析】本题考查了一次函数与二元一次方程(组):方程组的解就是两个相应的一次函数图象的交点坐标.先利用确定交点坐标,然后根据方程组的解就是两个相应的一次函数图象的交点坐标进行判断.
【详解】解:对于,当时,,
∴两直线交点坐标为,
∴方程组的解,
故选:A.
3.C
【分析】本题主要考查由实际问题抽象出二元一次方程组,解题的关键是理解题意,找到题目的等量关系.根据“鸡的数量兔的数量,鸡的脚的数量兔子的脚的数量”可列方程组.
【详解】解:设鸡有只,兔有只,
根据题意,可列方程组为,
故选:C.
4.A
【分析】此题主要考查了二元一次方程组与一次函数的关系,关键是掌握两函数图象的交点坐标就是两函数解析式组成的二元一次方程组的解.根据二元一次方程组的解的定义知,该方程组的解就是组成方程组的两个二元一次方程的图象的交点坐标.
【详解】解:直线与直线相交于点,
关于,的方程组的解为.
故选:A.
5.D
【分析】根据“如果乙给甲9只羊,那么甲的羊数为乙的2倍;如果甲给乙9只羊,那么两人的羊数相同”,列出二元一次方程组,即可求解,本题考查了二元一次方程组的实际应用,解题的关键是:正确理解题意,列出等量关系.
【详解】解:由“如果乙给甲9只羊,那么甲的羊数为乙的2倍,”可列式:,
由“如果甲给乙9只羊,那么两人的羊数相同,”可列式:,
根据题意可列二元一次方程组:,
故选:.
6.A
【分析】本题考查两条直线的交点问题,先联立方程组,然后两式相加消去,即可求出y,从而得解,掌握求两直线交点的方法是解题的关键.
【详解】解:联立方程组得:,
得:,
解得:,
即点A的纵坐标为2,
故选:A.
7.D
【分析】本题考查的是三元一次方程组的特殊解法,先根据表格信息建立方程组,再利用整体未知数的方法解方程即可;先求解,,再利用整体代入法可得答案.
【详解】解:当时,①,
当时,②,
当时,③,
当时,④,
③①得:,即,
④②得:,
∴,
∴,
∴;
故选D
8.A
【分析】本题考查了二元一次方程组的应用,设甲带钱为,乙带钱为,根据题意列出方程组即可求解,根据题意,找到等量关系,列出方程组是解题的关键.
【详解】解:设甲带钱为,乙带钱为,
由题意可得,
故选:.
9.B
【分析】本题考查了二元一次方程的变形,把x看作已知数求出y即可.
【详解】解:,
,
,
故选:B.
10.C
【分析】本题考查了一次函数与二元一次方程组之间的关系,联立函数式得方程组,由方程组得,根据点坐标恰好是格点,即可得到,解之即可求解,解题的关键是根据题意,联立方程组,对方程组的解进行分析.
【详解】解:由得,,
为整数,
,
,
又,
满足条件的有个,正比例函数解析式也有个,
故选:.
11.17
【分析】本题考查了解二元一次方程组和有理数的混合运算,得出关于a、b的方程组是解题的关键.
根据已知定义得出方程,,整理后得出关于a、b的方程组,求出a、b的值,再根据定义得出算式,最后求出答案即可.
【详解】解:根据题中的新定义化简已知等式,得,解得,
所以,
则.
故答案为:17.
12./
【分析】本题考查了一次函数与二元一次方程组.二元一次方程可以化为一次函数,两个二元一次方程组的解就是两个函数的交点坐标.
【详解】解:∵方程组的解是,
∴直线与的交点坐标是.
故答案为:.
13./
【分析】本题主要考查了一次函数与二元一次方程组之间的关系,先求出,再由两直线的交点的横纵坐标即为两直线解析式对应的二元一次方程组的解可得答案.
【详解】解:在中,当时,则,解得,
∴,
∵直线与直线相交于点,
∴关于,的方程组的解是,
故答案为:.
14.
【分析】此题主要考查了一次函数与二元一次方程组的关系,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数解析式,因此方程组的解就是两个相应的一次函数图象的交点坐标.把代入求出值可得出点坐标,即可得答案.
【详解】解:∵直线与直线相交于点,
∴,
∴,
∴方程组的解为.
故答案为:
15.6
【分析】本题考查了二元一次方程的应用,根据正方形的面积为81,可得正方形的边长为9,即,可列出一个关于a、b的方程,解方程组即可.
【详解】解:根据正方形的面积为81,可得正方形的边长为9,即,
小正方形的面积为9,则其边长为3,
∵大正方形边长为9,小正方形边长为3,
∴根据图示和题意得:,
解得:.
故答案为:6.
16.
【分析】本题考查了一次函数的交点与二元一次方程组解的关系,根据:一次函数的交点坐标就是以一次函数解析式所构成的二元一次方程组的解,即可求解,掌握一次函数的交点与二元一次方程组解的关系是解题的关键.
【详解】解:∵一次函数和的图象交于点,
∴关于的二元一次方程组的解为,
故答案为:.
17.
【分析】本题考查多项式乘以多项式,二元一次方程组的应用,代数式求值,解题的关键是明确不含的二次项,则二次项的系数为0.先利用多项式乘以多项式展开,进而得出二元一次方程组,求出、的值,代入计算即可.
【详解】解:
,
多项式与的乘积展开式中不含的二次项,且常数项为,
,
,
故.
故答案为:.
18.
【分析】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
设每支花卉成本是元,每支花卉成本是元,则每支花卉成本是元,根据每盒甲礼盒的总成本是每盒乙礼盒总成本的倍,可列出关于,的二元一次方程,解之可得出,继而可用含的代数式表示出每盒甲、乙、丙种礼盒的总成本,设该周末花店售出盒甲种礼盒,盒丙种礼盒,则售出盒乙种礼盒,根据三种礼盒的总成本恰好为总利润的倍,可列出关于,的二元一次方程,解之可得出,再用含,的代数式表示出该周末丙礼盒的总利润及三种礼盒的总利润,作比后即可得出结论.
【详解】解:设每支花卉成本是元,每支花卉成本是元,则每支花卉成本是元,
根据题意得:,
,
每盒甲种礼盒的总成本为:(元);
每盒乙种礼盒的总成本为:(元);
每盒丙种礼盒的总成本为:(元).
设该周末花店售出盒甲种礼盒,盒丙种礼盒,则售出盒乙种礼盒,
根据题意得:,
,
∴,
该周末丙礼盒的总利润为:(元),
三种礼盒的总利润为:(元),
该周末丙礼盒的总利润与三种礼盒的总利润的比值为:,
故答案为:.
19.(1)
(2)
【分析】本题考查了二元一次方程组的求解,掌握消元法是解题关键.
(1)利用代入消元法即可求解;
(2)综合利用代入消元法和加减消元法即可求解;
【详解】(1)解:
得:,
将①代入③得:,
解得:
将代入①得:
∴原方程组的解为:
(2)解:
得:
解得:
将代入①得:,
解得:
∴原方程组的解为:
20.(1)
(2)
【分析】此题考查了平方差公式,以及解二元一次方程组;熟练掌握公式及法则是解本题的关键.
(1)已知第二个等式左边利用平方差公式化简,把第一个等式代入求出的值即可;
(2)联立求出与的值即可.
【详解】(1)解:,,
,
;
(2)解:联立得:,
①+②得:,
解得:,
将代入②得
,
.
21.(1)第一、二次各购进水蜜桃30和50箱;
(2)利润为1540元
【分析】本题考查的是二元一次方程的应用,混合运算的实际应用,理解题意确定相等关系是解本题的关键;
(1)设第一、二次各购进水蜜桃a箱和b箱,利用“共购进水蜜桃80箱,已知第一、二次进货价分别为每箱60元、50元,且第二次比第一次多付款700元”,再建立方程求解即可;
(2)把打折前与打折后的利润相加即可.
【详解】(1)解:设第一、二次各购进水蜜桃a箱和b箱,由题意可得,
,
解得,,
答:第一、二次各购进水蜜桃30和50箱;
(2)该商店销售完全部水蜜桃所获得的利润为:
(元),
答:利润为1540元.
22.
【分析】本题主要考查了坐标与图形、二元一次方程组的应用等知识,正确列出二元一次方程并求解是解题关键.设小长方形的长为,宽为,根据题意列出二元一次方程组并求解,然后确定点的坐标即可.
【详解】解:设小长方形的长为,宽为,
依题意,得,
解得,
∴,,
∴点的坐标为.
23.(1)A型机器人模型的单价为500元,B型机器人模型的单价为300元
(2)一共需要4600元
【分析】本题主要考查了二元一次方程组的实际应用,有理数四则混合计算的实际应用:
(1)设A型机器人模型的单价为x元,B型机器人模型的单价为y元,根据A型机器人模型单价比B型机器人模型单价多200元,购买5台A型机器人模型的费用比购买7台B型机器人模型的费用多400元列出方程组求解即可;
(2)根据(1)所求分别求出两种机器人的费用,然后求和即可得到答案.
【详解】(1)解:设A型机器人模型的单价为x元,B型机器人模型的单价为y元.
由题意得,,
解得:,
答:A型机器人模型的单价为500元,B型机器人模型的单价为300元.
(2)解:元
答:一共需要4600元.
24.(1)张主任肯定搞错了,理由见解析
(2)2个水龙头
【分析】本题考查二元一次方程(组)的应用:
(1)设足球买了个,篮球买了个.根据题意列二元一次方程组,根据方程组的解是否为正整数即可解释;
(2)设张主任买了个足球,个水龙头,根据题意列二元一次方程,由,都是整数,且,确定n可能的取值,进而求出m的值,判断是否符合题意即可.
【详解】(1)解:设足球买了个,篮球买了个.
依题意,得,
解得,
,均为正整数,
不符合题意,即张主任肯定搞错了.
(2)解:设张主任买了个足球,个水龙头,则买的篮球的个数为个.
依题意,得,
整理,得.
,都是整数,且,
可能为2或3.
当时,,解得,符合题意;
当时,,解得,不符合题意,
他买了2个水龙头.
25.(1)
(2)
(3)或
【分析】(1)根据直线与x轴的交点可求得b的值,进而得到解析式,即可求得点的坐标;
(2)根据两个直线的解析式联立求得交点坐标D,以及点C的坐标,的面积以为底,以点D的横坐标的绝对值为高,即可求得面积;
(3)先求出的面积,根据两个三角形面积之间的关系求得面积,然后设出的长,根据面积分割法列得等式,求解即可,注意分情况讨论.
【详解】(1)解:∵直线与轴交于点,
∴,
解得:,
∴直线,
令,解得,
∴;
(2)解:∵直线与直线交于点,
∴,解得,
∴,
∵直线与轴交于点,
∴令,解得,
∴,
即,
∴;
(3)解:由(1)(2)可得,,,
∴,
∵的面积等于面积的,
∴,
设,
则,
即,
解得:,
∵,点在轴上,
当点E在点A左侧时,点E的横坐标为:,此时点,
当点E在点A右侧时,点E的横坐标为:,此时点,
∴点E的坐标为或.
【点睛】本题考查了直线围成的三角形的面积,待定系数法求一次函数的解析式,一次函数图像上点的坐标特征,分割法求三角形的面积,运用数形结合是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
