平行四边形的判定
图片预览
文档简介
班别:_ ____学号:______姓名:_______________ _
学案5 19.1.2 平行四边形的判定 (四)
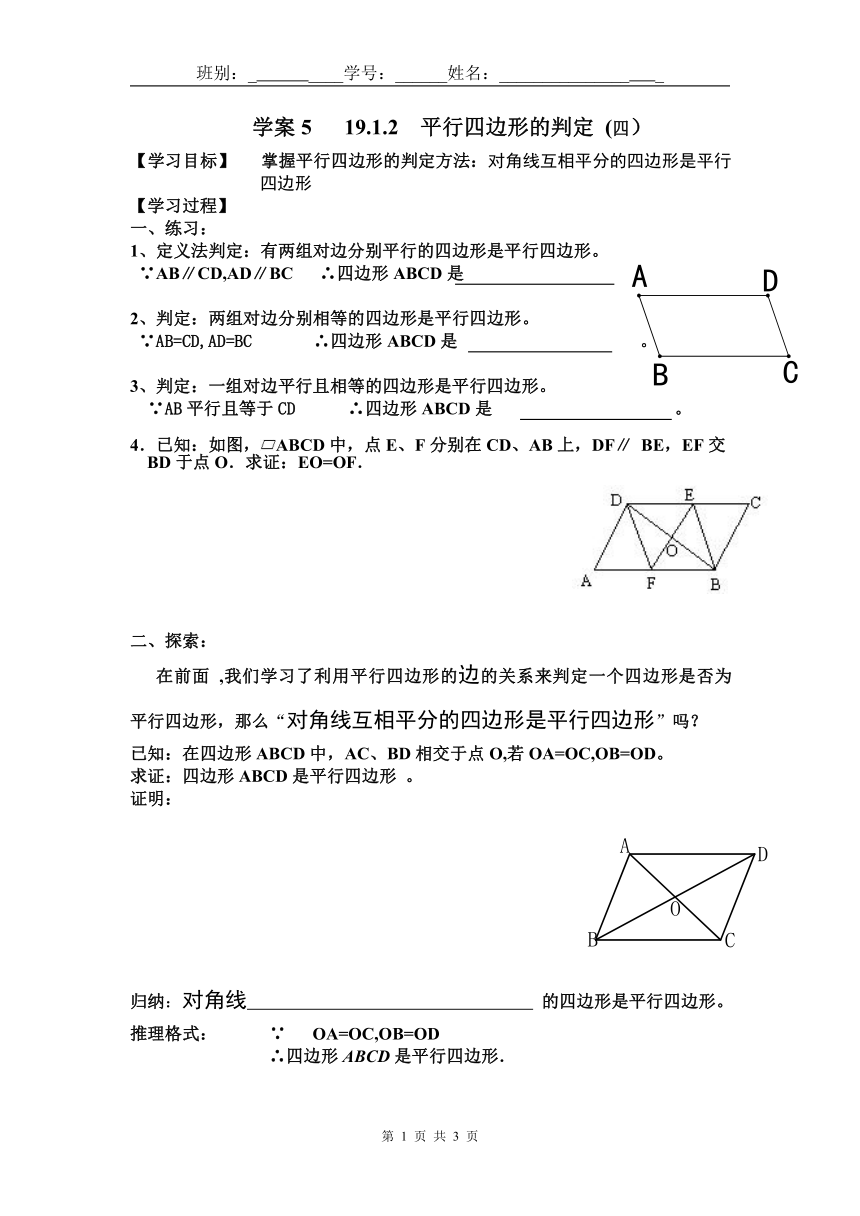
【学习目标】 掌握平行四边形的判定方法:对角线互相平分的四边形是平行四边形
【学习过程】
一、练习:
1、定义法判定:有两组对边分别平行的四边形是平行四边形。
∵AB∥CD,AD∥BC ∴四边形ABCD是
2、判定:两组对边分别相等的四边形是平行四边形。
∵AB=CD,AD=BC ∴四边形ABCD是 。
3、判定:一组对边平行且相等的四边形是平行四边形。
∵AB平行且等于CD ∴四边形ABCD是 。
4.已知:如图,ABCD中,点E、F分别在CD、AB上,DF∥ BE,EF交BD于点O.求证:EO=OF.
二、探索:
在前面 ,我们学习了利用平行四边形的边的关系来判定一个四边形是否为平行四边形,那么“对角线互相平分的四边形是平行四边形”吗?
已知:在四边形ABCD中,AC、BD相交于点O,若OA=OC,OB=OD。
求证:四边形ABCD是平行四边形 。
证明:
归纳:对角线 的四边形是平行四边形。
推理格式: ∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形.
三、例题:
已知:如图ABCD的对角线AC、BD交于点O,E、F是AC上的两点,
并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:
四、课堂练习:
1、如图,四边形ABCD,AC、BD相交于点O,若OA=OC,OB=OD,则四边形
ABCD是__________,根据是_____________________
2.如图,在四边形ABCD中,AC、BD相交于点O,若AC=10cm,BD=8cm,
那么当AO=__ _cm,DO=_ __cm时,四边形ABCD为平行四边形.
3、在 ABCD中,两条对角线AC、BD相交于点O,如图与△ABO面积相等的三角形有( )个。
A、1 B、2 C、3 D、4
4、如右图,在 ABCD中,对角线AC与BD交于O点,已知点E、F分别是
BD上的点,请你添加一个件 ,
使得四边形AFCE是一个平行四边形。
课外作业
1、判断题:
(1)对角线相等的四边形是平行四边形 ( )
(2)对角线互相平分的四边形是平行四边形 ( )
2、在四边形ABCD中,AC交BD 于点O,若AO=1/2AC,BO=1/2BD,则四边形 ABCD 是平行四边形。( )
3、下列条件中能判断四边形是平行四边形的是( ).
A、对角线互相垂直 B、对角线相等
C对角线互相垂直且相等 D对角线互相平分
4、已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN,且BM=DN 。
5、已知:在平行四边形ABCD中,对角线AC 、BD相交于点,M 、 N 、 P、 Q分别是OA 、OB 、OC 、 OD的中点。
求证 : 四边形MNPQ是平行四边形
第 3 页 共 3 页
学案5 19.1.2 平行四边形的判定 (四)
【学习目标】 掌握平行四边形的判定方法:对角线互相平分的四边形是平行四边形
【学习过程】
一、练习:
1、定义法判定:有两组对边分别平行的四边形是平行四边形。
∵AB∥CD,AD∥BC ∴四边形ABCD是
2、判定:两组对边分别相等的四边形是平行四边形。
∵AB=CD,AD=BC ∴四边形ABCD是 。
3、判定:一组对边平行且相等的四边形是平行四边形。
∵AB平行且等于CD ∴四边形ABCD是 。
4.已知:如图,ABCD中,点E、F分别在CD、AB上,DF∥ BE,EF交BD于点O.求证:EO=OF.
二、探索:
在前面 ,我们学习了利用平行四边形的边的关系来判定一个四边形是否为平行四边形,那么“对角线互相平分的四边形是平行四边形”吗?
已知:在四边形ABCD中,AC、BD相交于点O,若OA=OC,OB=OD。
求证:四边形ABCD是平行四边形 。
证明:
归纳:对角线 的四边形是平行四边形。
推理格式: ∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形.
三、例题:
已知:如图ABCD的对角线AC、BD交于点O,E、F是AC上的两点,
并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:
四、课堂练习:
1、如图,四边形ABCD,AC、BD相交于点O,若OA=OC,OB=OD,则四边形
ABCD是__________,根据是_____________________
2.如图,在四边形ABCD中,AC、BD相交于点O,若AC=10cm,BD=8cm,
那么当AO=__ _cm,DO=_ __cm时,四边形ABCD为平行四边形.
3、在 ABCD中,两条对角线AC、BD相交于点O,如图与△ABO面积相等的三角形有( )个。
A、1 B、2 C、3 D、4
4、如右图,在 ABCD中,对角线AC与BD交于O点,已知点E、F分别是
BD上的点,请你添加一个件 ,
使得四边形AFCE是一个平行四边形。
课外作业
1、判断题:
(1)对角线相等的四边形是平行四边形 ( )
(2)对角线互相平分的四边形是平行四边形 ( )
2、在四边形ABCD中,AC交BD 于点O,若AO=1/2AC,BO=1/2BD,则四边形 ABCD 是平行四边形。( )
3、下列条件中能判断四边形是平行四边形的是( ).
A、对角线互相垂直 B、对角线相等
C对角线互相垂直且相等 D对角线互相平分
4、已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN,且BM=DN 。
5、已知:在平行四边形ABCD中,对角线AC 、BD相交于点,M 、 N 、 P、 Q分别是OA 、OB 、OC 、 OD的中点。
求证 : 四边形MNPQ是平行四边形
第 3 页 共 3 页
