1.4整式的乘法第1课时-2023-2024学年七年级数学下册同步课件(北师大版)
文档属性
| 名称 | 1.4整式的乘法第1课时-2023-2024学年七年级数学下册同步课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 721.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第1课时
北师大版 数学 七年级下册
4 整式的乘法
第一章 整式的乘除
学习目标
1.掌握单项式与单项式相乘的运算法则.(重点)
2.能够灵活地进行单项式与单项式相乘的运算.(难点)
一、导入新课
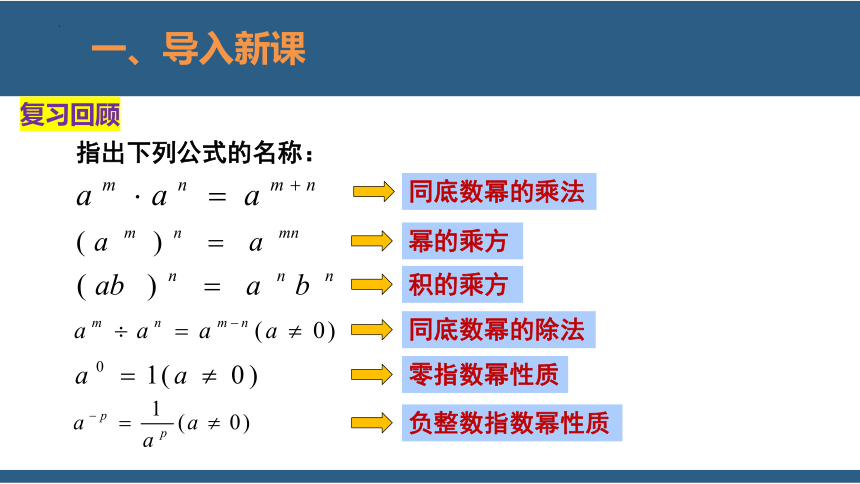
复习回顾
指出下列公式的名称:
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
零指数幂性质
负整数指数幂性质
一、导入新课
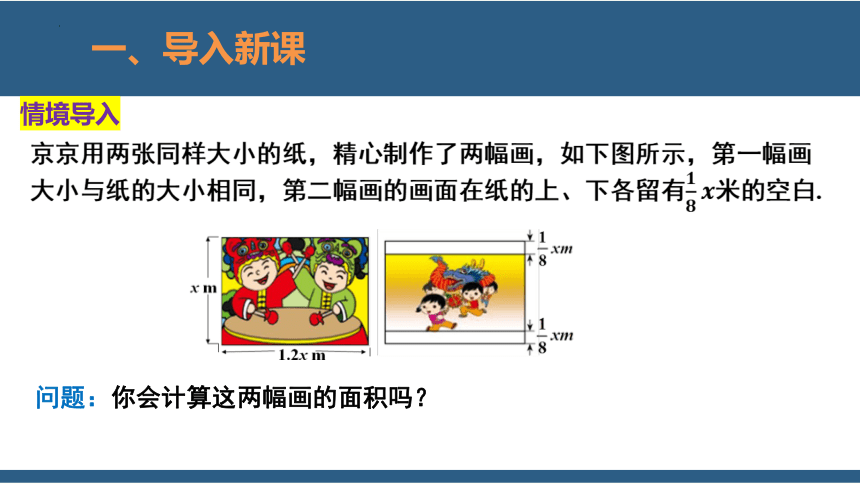
情境导入
京京用两张同样大小的纸,精心制作了两幅画,如下图所示,第一幅画大小与纸的大小相同,第二幅画的画面在纸的上、下各留有米的空白.
问题:你会计算这两幅画的面积吗?
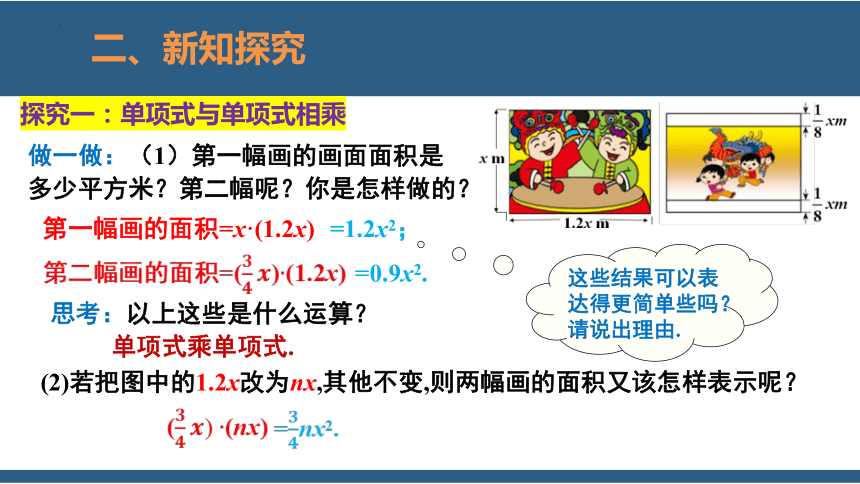
做一做:(1)第一幅画的画面面积是多少平方米?第二幅呢?你是怎样做的?
二、新知探究
探究一:单项式与单项式相乘
第一幅画的面积=x·(1.2x)
第二幅画的面积=()(1.2x)
=1.2x2;
=0.9x2.
这些结果可以表达得更简单些吗?请说出理由.
思考:以上这些是什么运算?
单项式乘单项式.
(2)若把图中的1.2x改为nx,其他不变,则两幅画的面积又该怎样表示呢?
((nx)
=nx2.
二、新知探究
想一想:(1)3a2b·2ab3及xyz·y2z等于什么?你是怎样计算的?
在你探索单项式乘法运算法则的过程中,运用了哪些运算律和运算法则?
3a2b·2ab3
=(3×2)·(a2·a)(b·b3)
=6a3b4.
xyz·2y2z
=x·(y·y2)(z·z)
=xy3z2.
运用了乘法交换律和结合律.
二、新知探究
知识归纳
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式与单项式的乘法法则
注意:(1)系数相乘;
(2)相同字母的幂相乘;
(3)其余字母连同它的指数不变,作为积的因式;
(4)单项式乘单项式的结果仍是一个单项式。
二、新知探究
(2)原式=[(-2)×(-3)] (a2a) b3 =6a3b3;
(3)原式=7xy2z 4x2y2z2
=(7×4) (xx2) (y2y2) (zz2)
=28x3y4z3.
跟踪练习
解:(1)原式=(2×) (x x) (y2 y)=;
1.计算:(1)2xy2 xy; (2) (-2a2b3 (-3a); (3)7xy2z (2xyz)2.
二、新知探究
单项式与单项式相乘
有理数的乘法与同底数幂的乘法
乘法交换律和结合律
转化
方法归纳
2.计算:(1) (-3x)2 ·4x2; (2)(-2a)3(-3a)2;
(3)(-4a2bc3)·(-5c5)·(ab2c).
二、新知探究
解:(1)原式=9x2·4x2
=(9×4)(x2·x2)
=36x4;
(2)原式=-8a3·9a2
=[(-8)×9](a3·a2)
=-72a5;
跟踪练习
解:原式=[(-4)×(-5)×](a2·a) (b·b2)(c3·c5·c)
=a3b3c9.
二、新知探究
单项式乘单项式的几点注意:
(1)在计算时,应先进行符号运算,积的系数等于各因式系数的积.
(2)注意按运算顺序计算,若有乘方,先算乘方.
(3)只在一个单项式里含有的字母,最后不要漏乘.
(4)单项式的法则适用于三个及以上的单项式相乘.
知识归纳
二、新知探究
探究二:单项式与单项式的乘法法则的应用
解:长方形的面积是xym2,
则绿化的面积是 x×y=xy(m2),
所以剩下的面积是xy-xy=xy(m2).
有一块长为xm,宽为ym的长方形空地,现在要在这块地中规划一块长xm,宽ym的长方形空地用于绿化,求绿化的面积和剩下的面积.
三、典例精析
解:(1)原式=-abc·a2b2·b2c4
=-(aa2)·(bb2b2)·(cc4)
=-a3b5c5.
例1 计算:-abc·a2b2·(-bc2)2;
(2)-6m2n·(x-y)3·mn2(y-x)2.
(2)原式=-6m2n·(x-y)3·mn2·(x-y)2
=-6×m3n3(x-y)5
=-2m3n3(x-y)5.
三、典例精析
例2:已知一个长方体包装箱,长为3a m,宽为2b m,高为ab m.
(1)求这个包装箱的体积;
(2)如果给这个包装箱的外表面都喷上油漆,那么共需喷多少平方米的油漆
解:因为3a·2b·ab=6a2b2(m3),
所以这个包装箱的体积为6a2b2 m3.
解:包装箱的表面积为2(3a·2b+3a·ab+2b·ab)=(12ab+6a2b+4ab2)m2,
所以共需喷(12ab+6a2b+4ab2)m2的油漆.
三、典例精析
例3:已知-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,求m2+n的值.
解:因为-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,
所以m2+n=22+3=4+3=7.
3.小刘做了四道题目:①3x3y·2xyz2=5x4y2z2;②2a2·(-3a)3=-54a6;
③(-m2n)2·(-8mn2)=-2m5n4;④-3a3b·(-3ab)=9a4b2.他做对的题目是( )A.①② B.③④ C.①②③ D.②③④
2.计算3a·(-2a)2的结果为 ( )
A.-12a3 B.-6a2 C.12a3 D.6a2
四、当堂练习
1.计算2a·ab的结果是 ( )
A.2ab B.2a2b C.3ab D.3a2b
B
C
B
5.若(-5am+1b2n-1)·2ab3=-10a4b4,则m-n的值为 ( )
A.-3 B.-1
C.1 D.3
四、当堂练习
4.一块长方形草坪的长是3xa+1 m,宽是2xb-1 m(a,b均为大于1的正整数),则长方形草坪的面积是 ( )
A.6xa-b m2 B.6xa+b m2
C.6xa+b-1 m2 D.6xa+b-2 m2
B
C
6.计算:x2y3·xyz= .
9.若单项式-12x2y2m与xn-2y6是同类项,则这两个单项式的积是 .
8.计算:3x2y·(-x6y)·y2z= .
(2)(-m3n)3·(-2m2n)4= .
7.计算:(1)(2xy2)2·x2y= ;
四、当堂练习
2x4y5
-2m17n7
-4x8y4z
-2x4y12
10.计算:3(a-b)2·[9(a-b)n+2]·(b-a)5= .
-27(a-b)n+9
x3y4z
四、当堂练习
解:(1)4xy2z·(-0.5x2y)3=4xy2z·(-x6y3)=-x7y5z.
(2)原式=3a2·(-ab)·(-8a6b3)=3a9b4.
(3)(-a4b)3·a-(2a4b)2·(-a5b)
=(-a12b3)·a-4a8b2·(-a5b)=-a13b3+3a13b3
=2a13b3.
11.计算:(1)4xy2z·(-0.5x2y)3; (2)3a2·(-ab)·(-2a2b)3; (3)(-a4b)3·a-(2a4b)2·(-a5b).
12.求图中阴影部分的面积.(列式写过程)
四、当堂练习
解:5a·(2a+a)-2a(5a-3a)
=5a·3a-2a·2a
=15a2-4a2
=11a2.
故阴影部分的面积为11a2.
四、当堂练习
13.已知9an-6b-2-n与-2a3m+1b2n的积与5a4b是同类项,求(m-n)2024的值.
解:因为9an-6b-2-n与-2a3m+1b2n的积与5a4b是同类项,
所以n-6+3m+1=4,-2-n+2n=1,
解得m=2,n=3,
所以(m-n)2022=(2-3)2022=1.
五、课堂小结
整式的乘法
单项式乘单项式法则
注意
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(1)在计算时,应先进行符号运算,积的系数等于各因式系数的积.(2)注意按运算顺序计算,若有乘方,先算乘方.(3)只在一个单项式里含有的字母,最后不要漏乘.(4)单项式的法则适用于三个及以上的单项式相乘.
六、作业布置
习题1.6
第1课时
北师大版 数学 七年级下册
4 整式的乘法
第一章 整式的乘除
学习目标
1.掌握单项式与单项式相乘的运算法则.(重点)
2.能够灵活地进行单项式与单项式相乘的运算.(难点)
一、导入新课
复习回顾
指出下列公式的名称:
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
零指数幂性质
负整数指数幂性质
一、导入新课
情境导入
京京用两张同样大小的纸,精心制作了两幅画,如下图所示,第一幅画大小与纸的大小相同,第二幅画的画面在纸的上、下各留有米的空白.
问题:你会计算这两幅画的面积吗?
做一做:(1)第一幅画的画面面积是多少平方米?第二幅呢?你是怎样做的?
二、新知探究
探究一:单项式与单项式相乘
第一幅画的面积=x·(1.2x)
第二幅画的面积=()(1.2x)
=1.2x2;
=0.9x2.
这些结果可以表达得更简单些吗?请说出理由.
思考:以上这些是什么运算?
单项式乘单项式.
(2)若把图中的1.2x改为nx,其他不变,则两幅画的面积又该怎样表示呢?
((nx)
=nx2.
二、新知探究
想一想:(1)3a2b·2ab3及xyz·y2z等于什么?你是怎样计算的?
在你探索单项式乘法运算法则的过程中,运用了哪些运算律和运算法则?
3a2b·2ab3
=(3×2)·(a2·a)(b·b3)
=6a3b4.
xyz·2y2z
=x·(y·y2)(z·z)
=xy3z2.
运用了乘法交换律和结合律.
二、新知探究
知识归纳
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式与单项式的乘法法则
注意:(1)系数相乘;
(2)相同字母的幂相乘;
(3)其余字母连同它的指数不变,作为积的因式;
(4)单项式乘单项式的结果仍是一个单项式。
二、新知探究
(2)原式=[(-2)×(-3)] (a2a) b3 =6a3b3;
(3)原式=7xy2z 4x2y2z2
=(7×4) (xx2) (y2y2) (zz2)
=28x3y4z3.
跟踪练习
解:(1)原式=(2×) (x x) (y2 y)=;
1.计算:(1)2xy2 xy; (2) (-2a2b3 (-3a); (3)7xy2z (2xyz)2.
二、新知探究
单项式与单项式相乘
有理数的乘法与同底数幂的乘法
乘法交换律和结合律
转化
方法归纳
2.计算:(1) (-3x)2 ·4x2; (2)(-2a)3(-3a)2;
(3)(-4a2bc3)·(-5c5)·(ab2c).
二、新知探究
解:(1)原式=9x2·4x2
=(9×4)(x2·x2)
=36x4;
(2)原式=-8a3·9a2
=[(-8)×9](a3·a2)
=-72a5;
跟踪练习
解:原式=[(-4)×(-5)×](a2·a) (b·b2)(c3·c5·c)
=a3b3c9.
二、新知探究
单项式乘单项式的几点注意:
(1)在计算时,应先进行符号运算,积的系数等于各因式系数的积.
(2)注意按运算顺序计算,若有乘方,先算乘方.
(3)只在一个单项式里含有的字母,最后不要漏乘.
(4)单项式的法则适用于三个及以上的单项式相乘.
知识归纳
二、新知探究
探究二:单项式与单项式的乘法法则的应用
解:长方形的面积是xym2,
则绿化的面积是 x×y=xy(m2),
所以剩下的面积是xy-xy=xy(m2).
有一块长为xm,宽为ym的长方形空地,现在要在这块地中规划一块长xm,宽ym的长方形空地用于绿化,求绿化的面积和剩下的面积.
三、典例精析
解:(1)原式=-abc·a2b2·b2c4
=-(aa2)·(bb2b2)·(cc4)
=-a3b5c5.
例1 计算:-abc·a2b2·(-bc2)2;
(2)-6m2n·(x-y)3·mn2(y-x)2.
(2)原式=-6m2n·(x-y)3·mn2·(x-y)2
=-6×m3n3(x-y)5
=-2m3n3(x-y)5.
三、典例精析
例2:已知一个长方体包装箱,长为3a m,宽为2b m,高为ab m.
(1)求这个包装箱的体积;
(2)如果给这个包装箱的外表面都喷上油漆,那么共需喷多少平方米的油漆
解:因为3a·2b·ab=6a2b2(m3),
所以这个包装箱的体积为6a2b2 m3.
解:包装箱的表面积为2(3a·2b+3a·ab+2b·ab)=(12ab+6a2b+4ab2)m2,
所以共需喷(12ab+6a2b+4ab2)m2的油漆.
三、典例精析
例3:已知-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,求m2+n的值.
解:因为-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,
所以m2+n=22+3=4+3=7.
3.小刘做了四道题目:①3x3y·2xyz2=5x4y2z2;②2a2·(-3a)3=-54a6;
③(-m2n)2·(-8mn2)=-2m5n4;④-3a3b·(-3ab)=9a4b2.他做对的题目是( )A.①② B.③④ C.①②③ D.②③④
2.计算3a·(-2a)2的结果为 ( )
A.-12a3 B.-6a2 C.12a3 D.6a2
四、当堂练习
1.计算2a·ab的结果是 ( )
A.2ab B.2a2b C.3ab D.3a2b
B
C
B
5.若(-5am+1b2n-1)·2ab3=-10a4b4,则m-n的值为 ( )
A.-3 B.-1
C.1 D.3
四、当堂练习
4.一块长方形草坪的长是3xa+1 m,宽是2xb-1 m(a,b均为大于1的正整数),则长方形草坪的面积是 ( )
A.6xa-b m2 B.6xa+b m2
C.6xa+b-1 m2 D.6xa+b-2 m2
B
C
6.计算:x2y3·xyz= .
9.若单项式-12x2y2m与xn-2y6是同类项,则这两个单项式的积是 .
8.计算:3x2y·(-x6y)·y2z= .
(2)(-m3n)3·(-2m2n)4= .
7.计算:(1)(2xy2)2·x2y= ;
四、当堂练习
2x4y5
-2m17n7
-4x8y4z
-2x4y12
10.计算:3(a-b)2·[9(a-b)n+2]·(b-a)5= .
-27(a-b)n+9
x3y4z
四、当堂练习
解:(1)4xy2z·(-0.5x2y)3=4xy2z·(-x6y3)=-x7y5z.
(2)原式=3a2·(-ab)·(-8a6b3)=3a9b4.
(3)(-a4b)3·a-(2a4b)2·(-a5b)
=(-a12b3)·a-4a8b2·(-a5b)=-a13b3+3a13b3
=2a13b3.
11.计算:(1)4xy2z·(-0.5x2y)3; (2)3a2·(-ab)·(-2a2b)3; (3)(-a4b)3·a-(2a4b)2·(-a5b).
12.求图中阴影部分的面积.(列式写过程)
四、当堂练习
解:5a·(2a+a)-2a(5a-3a)
=5a·3a-2a·2a
=15a2-4a2
=11a2.
故阴影部分的面积为11a2.
四、当堂练习
13.已知9an-6b-2-n与-2a3m+1b2n的积与5a4b是同类项,求(m-n)2024的值.
解:因为9an-6b-2-n与-2a3m+1b2n的积与5a4b是同类项,
所以n-6+3m+1=4,-2-n+2n=1,
解得m=2,n=3,
所以(m-n)2022=(2-3)2022=1.
五、课堂小结
整式的乘法
单项式乘单项式法则
注意
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(1)在计算时,应先进行符号运算,积的系数等于各因式系数的积.(2)注意按运算顺序计算,若有乘方,先算乘方.(3)只在一个单项式里含有的字母,最后不要漏乘.(4)单项式的法则适用于三个及以上的单项式相乘.
六、作业布置
习题1.6
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
