9.3 平行四边形(第1课时)(同步课件)-2023-2024学年八年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 9.3 平行四边形(第1课时)(同步课件)-2023-2024学年八年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第9章 · 中心对称图形——平行四边形
9.3 平行四边形(1)
第1课时 平行四边形及其性质
学习目标
1. 理解平行四边形的概念;
2.掌握平行四边形的基本性质并能简单应用.
问题情境
这些图片中有你熟悉的图形吗?这些图形有什么特征?
概念学习
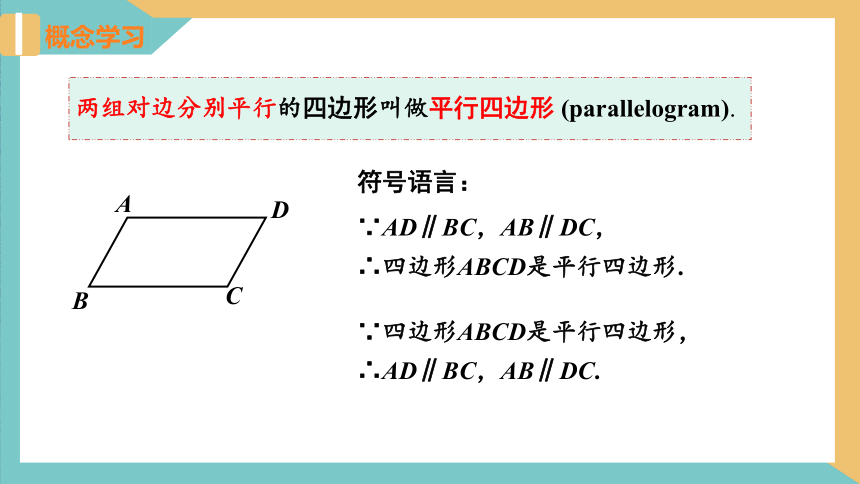
两组对边分别平行的四边形叫做平行四边形 (parallelogram).
A
B
C
D
如图,四边形ABCD是平行四边形,
记作:
读作:
(要注意字母顺序);
“ ABCD”
“平行四边形ABCD”.
概念学习
两组对边分别平行的四边形叫做平行四边形 (parallelogram).
A
B
C
D
符号语言:
∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC.
操作与探索
如图,O是 ABCD对角线AC的中点,用透明纸覆盖在图上,描出 ABCD,再用大头针钉在点O处,将透明纸上的 ABCD旋转180°,你有什么发现?
B
A
D
C
O
ABCD绕点O旋转180°后,能与原来的图形重合.
ABCD是中心对称图形,点O是它的对称中心.
B
A
D
C
操作与探索
如何证实呢?
∵O是AC的中点,
∴点A与点C重合,点C与点A重合;
B
A
D
C
O
由两条直线相交只有一个交点,可知AB和CB的交点B与CD和AD的交点D重合.
1
2
∵AB∥CD,可知∠1=∠2,
∴AB落在射线CD上;
3
4
∵ AB∥CD,可知∠3=∠4,
∴CB落在射线AD上.
同理,点D与点B重合.
∴ ABCD是中心对称图形.
操作与探索
B
A
D
C
1
2
3
4
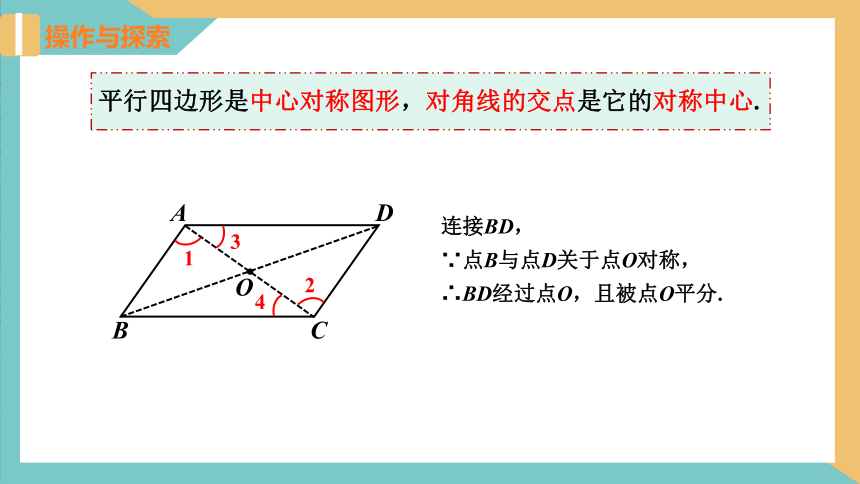
连接BD,
∵点B与点D关于点O对称,
∴BD经过点O,且被点O平分.
如何证实呢?
平行四边形是中心对称图形,对角线的交点是它的对称中心.
O
B
A
D
C
O
从证实 ABCD是中心对称图形的过程中,你发现平行四边形还有哪些性质?
操作与探索
B
A
D
C
对角线
边
角
对边相等
对角相等
互相平分
O
新知归纳
平行四边形的对边相等,对角相等,对角线互相平分.
B
A
D
C
∵四边形ABCD是平行四边形
∴AB=CD,____________.
( )
平行四边形的对边相等
∵四边形ABCD是平行四边形
∴_______________ ,∠BAD=∠DCB.
( )
∵四边形ABCD是平行四边形
∴OA=OC,__________.
( )
AD=BC
平行四边形的对角相等
OB=OD
平行四边形的对角线互相平分
∠ABC=∠ADC
A
B
C
D
E
F
例题讲解
例 已知:如图,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD.
(1) 图中有几个平行四边形?
解:(1)∵AB//DE,BC//EF,
∴四边形ABCE是平行四边形.
(两组对边分别平行的四边形叫做平行四边形)
同理,∵CA//FD,BC//EF,
∴四边形AFBC是平行四边形.
∵AB//DE,CA//FD,
∴四边形ABDC是平行四边形.
图中有哪些相等的线段、相等的角
例题讲解
例 已知:如图,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD.
(2)求证:A、B、C分别是△DEF各边的中点.
(2)证明:由(1)得四边形ABCE是平行四边形,
∴AE=BC(平行四边形的对边相等).
∵四边形AFBC是平行四边形
∴AF=BC(平行四边形的对边相等).
∴AE=AF.
同理BD=BF,CD=CE.
∴A、B、C分别是△DEF各边的中点.
A
B
C
D
E
F
例题讲解
A
B
C
D
E
F
例 已知:如图,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD.
(3)在图中,△ABC和△DEF的内角分别相等吗?为什么?
(3)证明:由(1)得四边形ABCE是平行四边形,
∴∠ABC=∠E(平行四边形的对角相等).
∵四边形AFBC是平行四边形
∴∠ACB=∠F(平行四边形的对角相等).
∵四边形ABDC是平行四边形
∴∠BAC=∠D(平行四边形的对角相等).
∴△ABC和△DEF的内角分别相等.
你还能得到哪些结论?
新知巩固
1. 如图所示,在 ABCD中,GH∥AB,EF∥AD,EF与GH相交于点O,则图中平行四边形的个数为______.
D
A
B
C
H
G
F
E
O
9个
新知巩固
2.如图,在 ABCD中,∠B=50°.求这个四边形的其他内角的度数.
A
D
C
B
证明:∵四边形ABCD是平行四边形,
∴AD//BC (平行四边形的对边平行).
∴∠A+∠B=180°(两直线平行,同旁内角互补).
∵∠B=50°,
∴∠A=130°.
∵四边形ABCD是平行四边形,
∴∠C=∠A=130°,∠D=∠B=50°
(平行四边形的对角相等).
新知巩固
变式1 在平行四边形ABCD中,若∠B+∠D=260°,你能很快求出∠A、∠B、∠C、∠D的度数吗?
A
D
C
B
证明:∵四边形ABCD是平行四边形,
∴∠C=∠A,∠B=∠D(平行四边形的对角相等).
∵∠B+∠D=260°,
∴∠B=∠D=130°.
∵四边形ABCD是平行四边形,
∴AD//BC,AB//DC (平行四边形的对边平行).
∴∠A+∠B=180°,∠B+∠C=180°
(两直线平行,同旁内角互补).
∴∠A=∠C=50°.
变式2 在平行四边形ABCD中,若∠A:∠B=2:1,你能求出∠C、 ∠D的度数吗?
新知巩固
B
A
D
C
O
3.如图, ABCD的对角线相交于点O,BC=7cm,BD=10cm,AC=6cm,求△AOD的周长.
证明:∵四边形ABCD是平行四边形,
∴AD=BC (平行四边形的对边相等).
OA=OC=AC,OA=OC=AC
(平行四边形的对角线互相平分).
∵BC=7cm,BD=10cm,AC=6cm,
∴AD=7cm,OA=×6=3cm,OD=×10=5cm,
△AOD的周长=AD+OA+OD=7+3+5=15cm.
新知巩固
变式 已知 ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F,则OE=OF吗?
B
A
D
C
O
E
F
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠OAE=∠OCF.
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴OE=OF.
课堂小结
9.3 平行四边形(1)
概念与符号表示
性质
对边平行且相等
对角相等,邻角互补
对角线互相平分
当堂检测
1. 平行四边形不一定具有的性质是( )A.对角线相等 B.对角相等C.对边平行且相等 D.对边相等
A
2. 在平行四边形ABCD中,下列结论一定成立的是( )A.AC⊥BD B.AB=ADC.∠A≠∠C D.∠A+∠B=180°
D
当堂检测
3.如图,BD∥EF,BC∥AF,CD∥EA,则图中平行四边形有( )A.2个 B.3个 C.4个 D.5个
C
D
B
A
E
F
B
当堂检测
4.如图,在 ABCD中,全等三角形共有( )A.2对 B.3对 C.4对 D.5对
B
A
D
C
O
C
5.在 ABCD中,∠A∶∠B∶∠C∶∠D可能是( )A.1∶2∶3∶4 B.2∶3∶2∶3 C.2∶2∶1∶1 D.2∶3∶3∶2
B
当堂检测
6.如图,在平行四边形ABCD中,BE平分∠ABC,若BC=6,DE=1,则平行四边形ABCD的周长等于________.
22
B
A
D
C
E
7.如图,在 ABCD中,AE⊥BC,AF⊥CD,E,F为垂足,若∠EAF=59°,则∠B=________°.
(6)
59
B
A
D
C
E
F
(7)
当堂检测
8.在 ABCD中,对角线AC和BD相交于点O,如果AC=10,BD=6,AB=m,那么m的取值范围是___________.
2<m<8
9. 已知在 ABCD中,AE平分∠BAD交BC于点E,点E将BC分成4 cm和6 cm长的两部分,则 ABCD的周长为_______________.
28 cm或32 cm
B
A
D
C
E
当堂检测
10.如图,四边形ABCD为平行四边形,则点B的坐标为___________.
B
A(-1, 2)
D(3, 2)
C(2, -1)
x
y
O
(-2,-1)
当堂检测
11.如图,已知 ABCD的周长为36 cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长多2 cm,求 ABCD各边的长.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AO=CO
(平行四边形的对边相等,对角线互相平分).
∵AB+CD+AD+BC=36 cm,
AO+AB+OB-(OB+BC+CO)=2 cm,
∴AB+BC=18 cm,AB-BC=2 cm,
∴AB=CD=10 cm,BC=AD=8 cm.
A
D
C
B
O
12.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.
E
D
C
F
B
A
(1)若∠EAF=56°,求∠B的度数;
解:(1)∵AE⊥BC,AF⊥CD,∴∠AEC=∠AFC=90°,在四边形AECF中,
∠C=360°-∠EAF-∠AEC-∠AFC
=360°-56°-90°-90°=124°,在 ABCD中,∠B=180°-∠C=180°-124°=56°.
当堂检测
12.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.
E
D
C
F
B
A
(2)若 ABCD的周长为48,AE=5,AF=10,求 ABCD的面积.
解:(2)设AB=x,则BC=24-x,
根据平行四边形的面积公式可得
10x=5(24-x),解得x=8,
∴平行四边形ABCD的面积为8×10=80.
当堂检测
第9章 · 中心对称图形——平行四边形
9.3 平行四边形(1)
第1课时 平行四边形及其性质
学习目标
1. 理解平行四边形的概念;
2.掌握平行四边形的基本性质并能简单应用.
问题情境
这些图片中有你熟悉的图形吗?这些图形有什么特征?
概念学习
两组对边分别平行的四边形叫做平行四边形 (parallelogram).
A
B
C
D
如图,四边形ABCD是平行四边形,
记作:
读作:
(要注意字母顺序);
“ ABCD”
“平行四边形ABCD”.
概念学习
两组对边分别平行的四边形叫做平行四边形 (parallelogram).
A
B
C
D
符号语言:
∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC.
操作与探索
如图,O是 ABCD对角线AC的中点,用透明纸覆盖在图上,描出 ABCD,再用大头针钉在点O处,将透明纸上的 ABCD旋转180°,你有什么发现?
B
A
D
C
O
ABCD绕点O旋转180°后,能与原来的图形重合.
ABCD是中心对称图形,点O是它的对称中心.
B
A
D
C
操作与探索
如何证实呢?
∵O是AC的中点,
∴点A与点C重合,点C与点A重合;
B
A
D
C
O
由两条直线相交只有一个交点,可知AB和CB的交点B与CD和AD的交点D重合.
1
2
∵AB∥CD,可知∠1=∠2,
∴AB落在射线CD上;
3
4
∵ AB∥CD,可知∠3=∠4,
∴CB落在射线AD上.
同理,点D与点B重合.
∴ ABCD是中心对称图形.
操作与探索
B
A
D
C
1
2
3
4
连接BD,
∵点B与点D关于点O对称,
∴BD经过点O,且被点O平分.
如何证实呢?
平行四边形是中心对称图形,对角线的交点是它的对称中心.
O
B
A
D
C
O
从证实 ABCD是中心对称图形的过程中,你发现平行四边形还有哪些性质?
操作与探索
B
A
D
C
对角线
边
角
对边相等
对角相等
互相平分
O
新知归纳
平行四边形的对边相等,对角相等,对角线互相平分.
B
A
D
C
∵四边形ABCD是平行四边形
∴AB=CD,____________.
( )
平行四边形的对边相等
∵四边形ABCD是平行四边形
∴_______________ ,∠BAD=∠DCB.
( )
∵四边形ABCD是平行四边形
∴OA=OC,__________.
( )
AD=BC
平行四边形的对角相等
OB=OD
平行四边形的对角线互相平分
∠ABC=∠ADC
A
B
C
D
E
F
例题讲解
例 已知:如图,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD.
(1) 图中有几个平行四边形?
解:(1)∵AB//DE,BC//EF,
∴四边形ABCE是平行四边形.
(两组对边分别平行的四边形叫做平行四边形)
同理,∵CA//FD,BC//EF,
∴四边形AFBC是平行四边形.
∵AB//DE,CA//FD,
∴四边形ABDC是平行四边形.
图中有哪些相等的线段、相等的角
例题讲解
例 已知:如图,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD.
(2)求证:A、B、C分别是△DEF各边的中点.
(2)证明:由(1)得四边形ABCE是平行四边形,
∴AE=BC(平行四边形的对边相等).
∵四边形AFBC是平行四边形
∴AF=BC(平行四边形的对边相等).
∴AE=AF.
同理BD=BF,CD=CE.
∴A、B、C分别是△DEF各边的中点.
A
B
C
D
E
F
例题讲解
A
B
C
D
E
F
例 已知:如图,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD.
(3)在图中,△ABC和△DEF的内角分别相等吗?为什么?
(3)证明:由(1)得四边形ABCE是平行四边形,
∴∠ABC=∠E(平行四边形的对角相等).
∵四边形AFBC是平行四边形
∴∠ACB=∠F(平行四边形的对角相等).
∵四边形ABDC是平行四边形
∴∠BAC=∠D(平行四边形的对角相等).
∴△ABC和△DEF的内角分别相等.
你还能得到哪些结论?
新知巩固
1. 如图所示,在 ABCD中,GH∥AB,EF∥AD,EF与GH相交于点O,则图中平行四边形的个数为______.
D
A
B
C
H
G
F
E
O
9个
新知巩固
2.如图,在 ABCD中,∠B=50°.求这个四边形的其他内角的度数.
A
D
C
B
证明:∵四边形ABCD是平行四边形,
∴AD//BC (平行四边形的对边平行).
∴∠A+∠B=180°(两直线平行,同旁内角互补).
∵∠B=50°,
∴∠A=130°.
∵四边形ABCD是平行四边形,
∴∠C=∠A=130°,∠D=∠B=50°
(平行四边形的对角相等).
新知巩固
变式1 在平行四边形ABCD中,若∠B+∠D=260°,你能很快求出∠A、∠B、∠C、∠D的度数吗?
A
D
C
B
证明:∵四边形ABCD是平行四边形,
∴∠C=∠A,∠B=∠D(平行四边形的对角相等).
∵∠B+∠D=260°,
∴∠B=∠D=130°.
∵四边形ABCD是平行四边形,
∴AD//BC,AB//DC (平行四边形的对边平行).
∴∠A+∠B=180°,∠B+∠C=180°
(两直线平行,同旁内角互补).
∴∠A=∠C=50°.
变式2 在平行四边形ABCD中,若∠A:∠B=2:1,你能求出∠C、 ∠D的度数吗?
新知巩固
B
A
D
C
O
3.如图, ABCD的对角线相交于点O,BC=7cm,BD=10cm,AC=6cm,求△AOD的周长.
证明:∵四边形ABCD是平行四边形,
∴AD=BC (平行四边形的对边相等).
OA=OC=AC,OA=OC=AC
(平行四边形的对角线互相平分).
∵BC=7cm,BD=10cm,AC=6cm,
∴AD=7cm,OA=×6=3cm,OD=×10=5cm,
△AOD的周长=AD+OA+OD=7+3+5=15cm.
新知巩固
变式 已知 ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F,则OE=OF吗?
B
A
D
C
O
E
F
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠OAE=∠OCF.
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴OE=OF.
课堂小结
9.3 平行四边形(1)
概念与符号表示
性质
对边平行且相等
对角相等,邻角互补
对角线互相平分
当堂检测
1. 平行四边形不一定具有的性质是( )A.对角线相等 B.对角相等C.对边平行且相等 D.对边相等
A
2. 在平行四边形ABCD中,下列结论一定成立的是( )A.AC⊥BD B.AB=ADC.∠A≠∠C D.∠A+∠B=180°
D
当堂检测
3.如图,BD∥EF,BC∥AF,CD∥EA,则图中平行四边形有( )A.2个 B.3个 C.4个 D.5个
C
D
B
A
E
F
B
当堂检测
4.如图,在 ABCD中,全等三角形共有( )A.2对 B.3对 C.4对 D.5对
B
A
D
C
O
C
5.在 ABCD中,∠A∶∠B∶∠C∶∠D可能是( )A.1∶2∶3∶4 B.2∶3∶2∶3 C.2∶2∶1∶1 D.2∶3∶3∶2
B
当堂检测
6.如图,在平行四边形ABCD中,BE平分∠ABC,若BC=6,DE=1,则平行四边形ABCD的周长等于________.
22
B
A
D
C
E
7.如图,在 ABCD中,AE⊥BC,AF⊥CD,E,F为垂足,若∠EAF=59°,则∠B=________°.
(6)
59
B
A
D
C
E
F
(7)
当堂检测
8.在 ABCD中,对角线AC和BD相交于点O,如果AC=10,BD=6,AB=m,那么m的取值范围是___________.
2<m<8
9. 已知在 ABCD中,AE平分∠BAD交BC于点E,点E将BC分成4 cm和6 cm长的两部分,则 ABCD的周长为_______________.
28 cm或32 cm
B
A
D
C
E
当堂检测
10.如图,四边形ABCD为平行四边形,则点B的坐标为___________.
B
A(-1, 2)
D(3, 2)
C(2, -1)
x
y
O
(-2,-1)
当堂检测
11.如图,已知 ABCD的周长为36 cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长多2 cm,求 ABCD各边的长.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AO=CO
(平行四边形的对边相等,对角线互相平分).
∵AB+CD+AD+BC=36 cm,
AO+AB+OB-(OB+BC+CO)=2 cm,
∴AB+BC=18 cm,AB-BC=2 cm,
∴AB=CD=10 cm,BC=AD=8 cm.
A
D
C
B
O
12.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.
E
D
C
F
B
A
(1)若∠EAF=56°,求∠B的度数;
解:(1)∵AE⊥BC,AF⊥CD,∴∠AEC=∠AFC=90°,在四边形AECF中,
∠C=360°-∠EAF-∠AEC-∠AFC
=360°-56°-90°-90°=124°,在 ABCD中,∠B=180°-∠C=180°-124°=56°.
当堂检测
12.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.
E
D
C
F
B
A
(2)若 ABCD的周长为48,AE=5,AF=10,求 ABCD的面积.
解:(2)设AB=x,则BC=24-x,
根据平行四边形的面积公式可得
10x=5(24-x),解得x=8,
∴平行四边形ABCD的面积为8×10=80.
当堂检测
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
