第16章二次根式复盘提升 单元复习课件(共31张PPT)
文档属性
| 名称 | 第16章二次根式复盘提升 单元复习课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 22.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 07:49:42 | ||
图片预览










文档简介
(共31张PPT)
第16章
二次根式
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
单元复盘提升
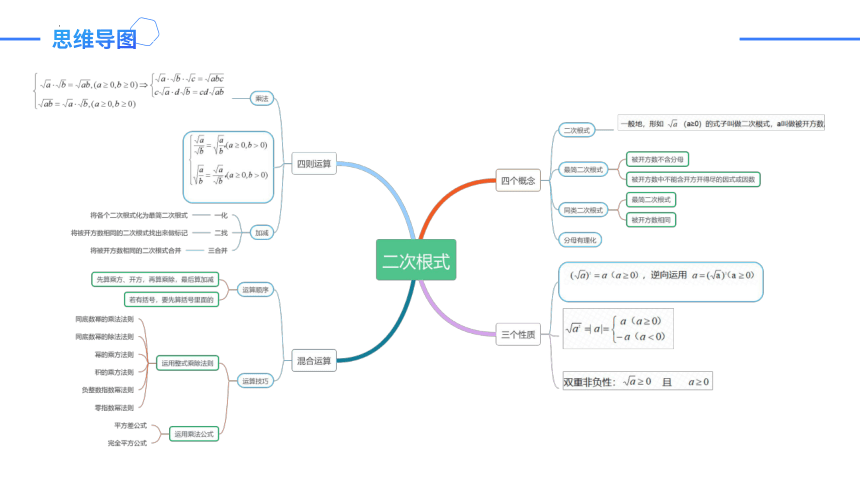
思维导图
知识串讲
平方、开平方、平方根、算数平方根的概念识别
01
①平方:平方是一种运算。比如:a的平方表示a×a,简写成a2.
例如:4的平方,为4×4=42=16
②开平方:开平方指一种数学的运算方式,求一个数的平方根的运算叫做开平方.
例如:4进行开平方,为
③平方根:平方根又叫二次方根,表示为( ).
例如:4的平方根,为
一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根.
④算数平方根:正数的平方根有两个,它们互为相反数,
其中属于非负数的平方根就是这个数的算术平方根.
例如:4的算术平方根,为2.
知识串讲
二次根式的定义及性质
02
①定义:一般地,形如 (a≥0)的式子叫做二次根式,a叫做被开方数。
②有意义的条件: 在实数范围内有意义
③性质:
,逆向运用
双重非负性: 且
知识串讲
二次根式的乘除
03
①二次根式的乘法:
②二次根式的除法:
知识串讲
二次根式的相关概念
04
①最简二次根式:
②同类二次根式:
被开方数不含分母
被开方数中不含能开得尽方的因数或因式
最简二次根式
被开方数相同
定义:几个二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式叫做同类二次根式.
知识串讲
二次根式的加减
05
二次根式的加减:
类似合并同类项:
一化:将各个二次根式化为最简二次根式
二找:将被开方数相同的二次根式找出做标记
三合并:将被开方数相同的二次根式合并
被开方数相同
最简二次根式
可以先将二次根式化成_____________,再将________________的二次根式进行合并.
知识串讲
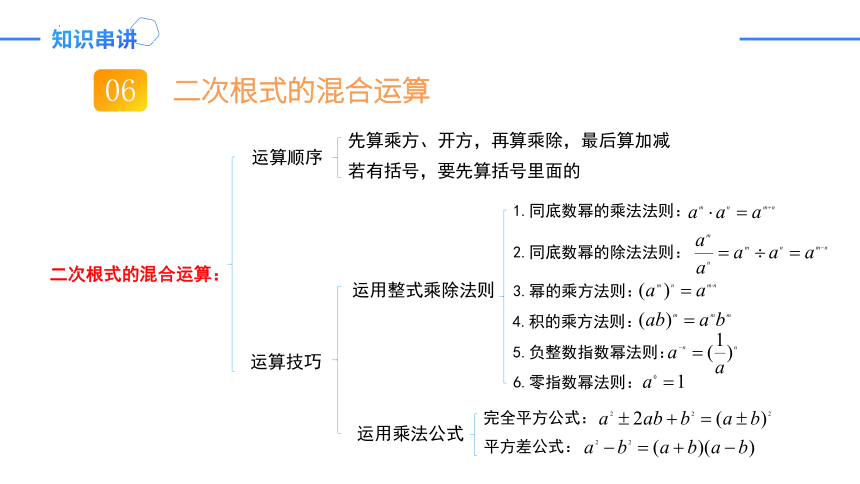
二次根式的混合运算
06
二次根式的混合运算:
运算顺序
运算技巧
先算乘方、开方,再算乘除,最后算加减
若有括号,要先算括号里面的
运用整式乘除法则
运用乘法公式
1.同底数幂的乘法法则:
2.同底数幂的除法法则:
4.积的乘方法则:
3.幂的乘方法则:
5.负整数指数幂法则:
6.零指数幂法则:
完全平方公式:
平方差公式:
考点梳理
考点一:二次根式的相关概念有意义的条件
例1
(2)使代数式 有意义的自变量x的取值范围是( )
A. B. C. D.
(1)下列式子中,是二次根式的是( )
A. B. C. D.
A
(3)若 有意义,则 .
3
C
刻意练习
练1
求下列二次根式中字母a的取值范围:
解:(1)由题意得
(3)∵(a+3)2≥0,∴a为全体实数;
(4)由题意得 ∴a≥0且a≠1.
考点梳理
考点二:二次根式的性质
例2
(2)若 ,求a -b+c的值.
解:
由题意可知a-2=0,b-3=0,c-4=0,
解得a=2,b=3,c=4.
所以a-b+c=2-3+4=3.
C
考点梳理
考点二:二次根式的性质
例3
化简:
解:
刻意练习
练2
(2) 比较下列两组数的大小(在横线上填“>”“<”
或“=”):
>
<
(1)计算:
考点梳理
考点三:二次根式的运算及应用
例4
计算:
解:
考点梳理
考点三:二次根式的运算及应用
例5
计算:
解:
考点梳理
例6
已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
考点三:二次根式的运算及应用
刻意练习
练3
(1)下列运算正确的是( )
C
A
刻意练习
练4
A
(2)若等腰三角形底边长为 ,底边的高为
则三角形的面积为 .
刻意练习
练5
考点梳理
考点四:二次根式的化简求值
例7
刻意练习
练6
刻意练习
练7
C
B
模型总结
模型一:分类讨论
已知a是实数,求 的值.
解: 分三种情况讨论:
当a≤-2时,原式=(-a-2)-[-(a-1)]=-a-2+a-1=-3;
当-2<a≤1时,原式=(a+2)+(a-1)= 2a+1;
当a>1时,原式=(a+2)-(a-1)=3.
刻意练习
练习
2
-1或-7
模型总结
模型一:整体代换
已知 ,求 的值.
∴
刻意练习
练习
2
2024
模型总结
模型三:类比思维
阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 ,善于思考的小明进行了以下探索:
设 (其中a、b、m、n均为整数),则有 这样小明就找到了一种把类似 的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
模型总结
模型三:类比思维
(1)当a、b、m、n均为正整数时,若 ,
用含m、n的式子分别表示a,b,得
a=_______;b=______;
(2)利用所探索的结论,用完全平方式表示出:
(3)请化简:
m2+3n2
2mn
解:
刻意练习
练习
课程小结
加、减、乘、除运算
二次根式
性质
最简二次根式
第16章
二次根式
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
单元复盘提升
思维导图
知识串讲
平方、开平方、平方根、算数平方根的概念识别
01
①平方:平方是一种运算。比如:a的平方表示a×a,简写成a2.
例如:4的平方,为4×4=42=16
②开平方:开平方指一种数学的运算方式,求一个数的平方根的运算叫做开平方.
例如:4进行开平方,为
③平方根:平方根又叫二次方根,表示为( ).
例如:4的平方根,为
一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根.
④算数平方根:正数的平方根有两个,它们互为相反数,
其中属于非负数的平方根就是这个数的算术平方根.
例如:4的算术平方根,为2.
知识串讲
二次根式的定义及性质
02
①定义:一般地,形如 (a≥0)的式子叫做二次根式,a叫做被开方数。
②有意义的条件: 在实数范围内有意义
③性质:
,逆向运用
双重非负性: 且
知识串讲
二次根式的乘除
03
①二次根式的乘法:
②二次根式的除法:
知识串讲
二次根式的相关概念
04
①最简二次根式:
②同类二次根式:
被开方数不含分母
被开方数中不含能开得尽方的因数或因式
最简二次根式
被开方数相同
定义:几个二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式叫做同类二次根式.
知识串讲
二次根式的加减
05
二次根式的加减:
类似合并同类项:
一化:将各个二次根式化为最简二次根式
二找:将被开方数相同的二次根式找出做标记
三合并:将被开方数相同的二次根式合并
被开方数相同
最简二次根式
可以先将二次根式化成_____________,再将________________的二次根式进行合并.
知识串讲
二次根式的混合运算
06
二次根式的混合运算:
运算顺序
运算技巧
先算乘方、开方,再算乘除,最后算加减
若有括号,要先算括号里面的
运用整式乘除法则
运用乘法公式
1.同底数幂的乘法法则:
2.同底数幂的除法法则:
4.积的乘方法则:
3.幂的乘方法则:
5.负整数指数幂法则:
6.零指数幂法则:
完全平方公式:
平方差公式:
考点梳理
考点一:二次根式的相关概念有意义的条件
例1
(2)使代数式 有意义的自变量x的取值范围是( )
A. B. C. D.
(1)下列式子中,是二次根式的是( )
A. B. C. D.
A
(3)若 有意义,则 .
3
C
刻意练习
练1
求下列二次根式中字母a的取值范围:
解:(1)由题意得
(3)∵(a+3)2≥0,∴a为全体实数;
(4)由题意得 ∴a≥0且a≠1.
考点梳理
考点二:二次根式的性质
例2
(2)若 ,求a -b+c的值.
解:
由题意可知a-2=0,b-3=0,c-4=0,
解得a=2,b=3,c=4.
所以a-b+c=2-3+4=3.
C
考点梳理
考点二:二次根式的性质
例3
化简:
解:
刻意练习
练2
(2) 比较下列两组数的大小(在横线上填“>”“<”
或“=”):
>
<
(1)计算:
考点梳理
考点三:二次根式的运算及应用
例4
计算:
解:
考点梳理
考点三:二次根式的运算及应用
例5
计算:
解:
考点梳理
例6
已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
考点三:二次根式的运算及应用
刻意练习
练3
(1)下列运算正确的是( )
C
A
刻意练习
练4
A
(2)若等腰三角形底边长为 ,底边的高为
则三角形的面积为 .
刻意练习
练5
考点梳理
考点四:二次根式的化简求值
例7
刻意练习
练6
刻意练习
练7
C
B
模型总结
模型一:分类讨论
已知a是实数,求 的值.
解: 分三种情况讨论:
当a≤-2时,原式=(-a-2)-[-(a-1)]=-a-2+a-1=-3;
当-2<a≤1时,原式=(a+2)+(a-1)= 2a+1;
当a>1时,原式=(a+2)-(a-1)=3.
刻意练习
练习
2
-1或-7
模型总结
模型一:整体代换
已知 ,求 的值.
∴
刻意练习
练习
2
2024
模型总结
模型三:类比思维
阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 ,善于思考的小明进行了以下探索:
设 (其中a、b、m、n均为整数),则有 这样小明就找到了一种把类似 的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
模型总结
模型三:类比思维
(1)当a、b、m、n均为正整数时,若 ,
用含m、n的式子分别表示a,b,得
a=_______;b=______;
(2)利用所探索的结论,用完全平方式表示出:
(3)请化简:
m2+3n2
2mn
解:
刻意练习
练习
课程小结
加、减、乘、除运算
二次根式
性质
最简二次根式
