8.3.2 平方差公式 课时作业(含答案) 2023-2024学年初中数学沪科版七年级下册
文档属性
| 名称 | 8.3.2 平方差公式 课时作业(含答案) 2023-2024学年初中数学沪科版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 159.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 12:48:56 | ||
图片预览


文档简介
8.3 完全平方公式与平方差公式
第2课时 平方差公式
【基础达标作业】
1.下列各式中不能用平方差公式进行计算的是 ( )
A.(m-n)(m+n)
B.(2x+y)(y-2x)
C.(-x-y)(x+y)
D.(a+b-c)(a-b+c)
2.下列计算错误的是 ( )
A.(2a+b)(2a-b)=4a2-b2
B.(2x+3)(2y-3)=4xy-9
C.(a-2b)(a+2b)=a2-4b2
D.(2x+1)(2x-1)=4x2-1
3.若实数m,n满足(m2+2n2+5)(m2+2n2-5)=0,则m2+2n2的值为(A)
A.5 B.2.5
C.2.5或5 D.5或-5
4.填空:
(1)(-5s+6t)( )=25s2-36t2.
(2)(x-2y)2-(x+2y)(2y-x)= .
(3)999×1001-10002= .
5.运用平方差公式计算:
(1)(-3m+2n)(-3m-2n);
(2)(a+b)(a-b)+(a+2b)(a-2b).
6.解方程:2(x+3)(x-3)=x2+(x-1)(x+1)+2x.
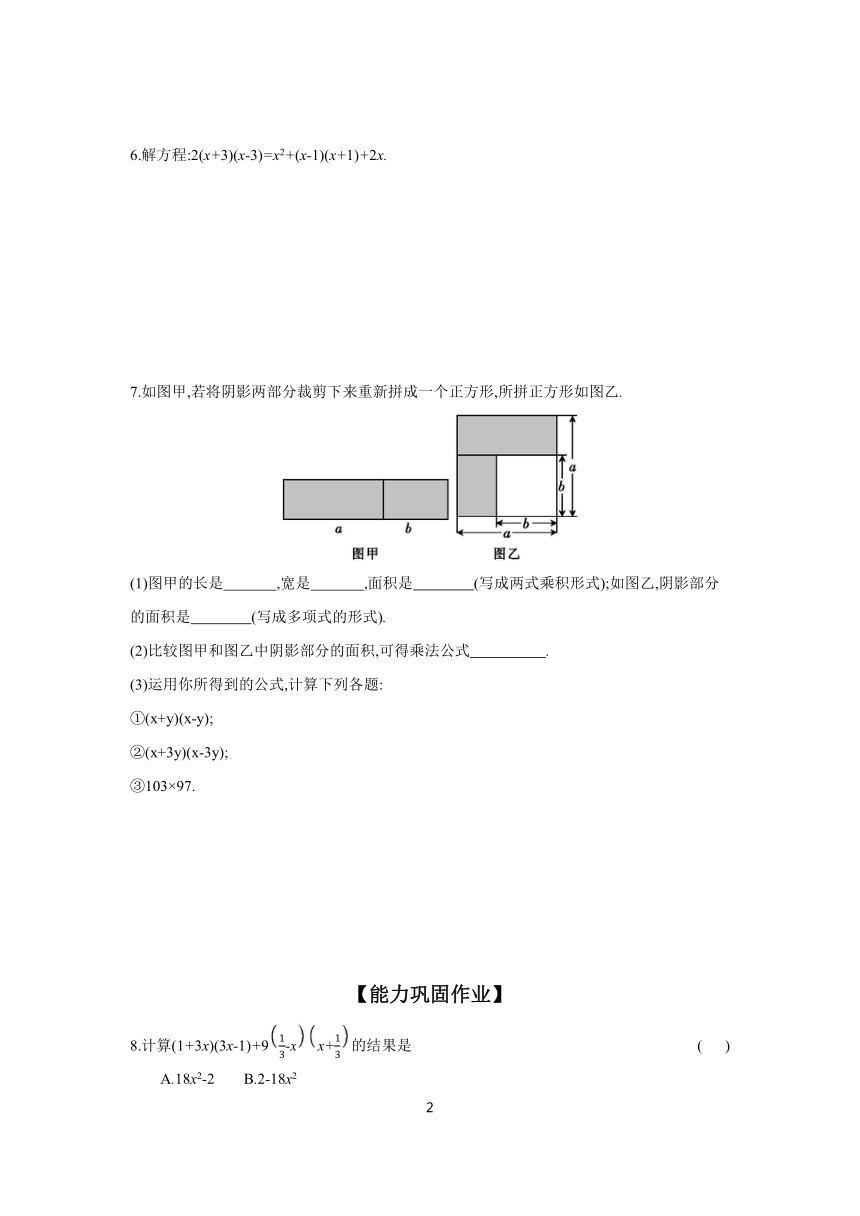
7.如图甲,若将阴影两部分裁剪下来重新拼成一个正方形,所拼正方形如图乙.
(1)图甲的长是 ,宽是 ,面积是 (写成两式乘积形式);如图乙,阴影部分的面积是 (写成多项式的形式).
(2)比较图甲和图乙中阴影部分的面积,可得乘法公式 .
(3)运用你所得到的公式,计算下列各题:
①(x+y)(x-y);
②(x+3y)(x-3y);
③103×97.
【能力巩固作业】
8.计算(1+3x)(3x-1)+9-xx+的结果是 ( )
A.18x2-2 B.2-18x2
C.0 D.8x2
9.对实数a,b定义运算:a※b=a(b+1),例如2※3=2(3+1)=8,则(x-1)※x的结果为 .
10.已知x-y=2,y-z=2,x+z=-14,则x2-z2的值为 .
11.已知(a+b-3)2+|a-b+5|=0,则a2-b2= .
12.计算:(1)(3n+1)(3n-1)-(3-n)(3+n);
(2)(m4+16)(m2+4)(m+2)(m-2).
【素养拓展作业】
13.已知a+b=4,a2-b2=12,求a、b的值.
14.观察下列等式:1×3=22-1,2×4=32-1,3×5=42-1,4×6=52-1,…,10×12=112-1,….请你将发现的规律用只含有一个字母的式子表示出来.
15.(a-b)(a+b)=a2-b2;
(a-b)(a2+ab+b2)=a3-b3;
(a-b)(a3+a2b+ab2+b3)=a4-b4;…
利用你的发现的规律解决下列问题.
(1)(a-b)(a4+a3b+a2b2+ab3+b4)= (直接填空).
(2)(a-b)(an-1+an-2b+an-3b2+…+abn-2+bn-1)= (直接填空).
(3)利用(2)中得出的结论求62023+62022+…+62+6+1的值.
参考答案
基础达标作业
1.C 2.B 3.A
4.(1)-5s-6t (2)2x2-4xy (3)-1
5.解:(1)原式=9m2-4n2.
(2)原式=a2-b2+a2-4b2=2a2-5b2.
6.解:2x2-18=x2+x2-1+2x,
所以2x=-17,x=-.
7.解:(1)图甲的长是a+b,宽是a-b,面积是(a+b)(a-b)(写成两式乘积形式);如图乙所示,阴影部分的面积是a2-b2(写成多项式的形式).故答案为(a+b),(a-b),(a+b)(a-b),a2-b2.
(2)比较图甲和图乙中阴影部分的面积,可得乘法公式(a+b)(a-b)=a2-b2.故答案为(a+b)(a-b)=a2-b2.
(3)①(x+y)(x-y)=x2-y2;
②(x+3y)(x-3y)=x2-9y2;
③103×97=(100+3)(100-3)=1002-9=9991.
能力巩固作业
8.C
9.x2-1 10.-56 11.-15
12.解:(1)原式=(3n+1)(3n-1)-(3-n)(3+n)
=9n2-1-(9-n2)
=10n2-10.
(2)原式=(m4+16)(m2+4)(m2-4)
=(m4+16)(m4-16)
=m8-256.
素养拓展作业
13.解:因为(a+b)(a-b)=a2-b2,
所以a-b=3,解方程组得
所以a、b的值分别为、.
14.解:因为2×4=(3-1)(3+1)=32-1,3×5=(4-1)(4+1)=42-1,…,所以得出规律(n-1)(n+1)=n2-1(n为大于1的整数).
15.解:(1)(a-b)(a4+a3b+a2b2+ab3+b4)=a5-b5.故答案为a5-b5.
(2)(a-b)(an-1+an-2b+an-3b2+…+abn-2+bn-1)=an-bn.故答案为an-bn.
(3)62019+62018+…+62+6+1=(6-1)(62019+62018+…+62+6)×=.
2
第2课时 平方差公式
【基础达标作业】
1.下列各式中不能用平方差公式进行计算的是 ( )
A.(m-n)(m+n)
B.(2x+y)(y-2x)
C.(-x-y)(x+y)
D.(a+b-c)(a-b+c)
2.下列计算错误的是 ( )
A.(2a+b)(2a-b)=4a2-b2
B.(2x+3)(2y-3)=4xy-9
C.(a-2b)(a+2b)=a2-4b2
D.(2x+1)(2x-1)=4x2-1
3.若实数m,n满足(m2+2n2+5)(m2+2n2-5)=0,则m2+2n2的值为(A)
A.5 B.2.5
C.2.5或5 D.5或-5
4.填空:
(1)(-5s+6t)( )=25s2-36t2.
(2)(x-2y)2-(x+2y)(2y-x)= .
(3)999×1001-10002= .
5.运用平方差公式计算:
(1)(-3m+2n)(-3m-2n);
(2)(a+b)(a-b)+(a+2b)(a-2b).
6.解方程:2(x+3)(x-3)=x2+(x-1)(x+1)+2x.
7.如图甲,若将阴影两部分裁剪下来重新拼成一个正方形,所拼正方形如图乙.
(1)图甲的长是 ,宽是 ,面积是 (写成两式乘积形式);如图乙,阴影部分的面积是 (写成多项式的形式).
(2)比较图甲和图乙中阴影部分的面积,可得乘法公式 .
(3)运用你所得到的公式,计算下列各题:
①(x+y)(x-y);
②(x+3y)(x-3y);
③103×97.
【能力巩固作业】
8.计算(1+3x)(3x-1)+9-xx+的结果是 ( )
A.18x2-2 B.2-18x2
C.0 D.8x2
9.对实数a,b定义运算:a※b=a(b+1),例如2※3=2(3+1)=8,则(x-1)※x的结果为 .
10.已知x-y=2,y-z=2,x+z=-14,则x2-z2的值为 .
11.已知(a+b-3)2+|a-b+5|=0,则a2-b2= .
12.计算:(1)(3n+1)(3n-1)-(3-n)(3+n);
(2)(m4+16)(m2+4)(m+2)(m-2).
【素养拓展作业】
13.已知a+b=4,a2-b2=12,求a、b的值.
14.观察下列等式:1×3=22-1,2×4=32-1,3×5=42-1,4×6=52-1,…,10×12=112-1,….请你将发现的规律用只含有一个字母的式子表示出来.
15.(a-b)(a+b)=a2-b2;
(a-b)(a2+ab+b2)=a3-b3;
(a-b)(a3+a2b+ab2+b3)=a4-b4;…
利用你的发现的规律解决下列问题.
(1)(a-b)(a4+a3b+a2b2+ab3+b4)= (直接填空).
(2)(a-b)(an-1+an-2b+an-3b2+…+abn-2+bn-1)= (直接填空).
(3)利用(2)中得出的结论求62023+62022+…+62+6+1的值.
参考答案
基础达标作业
1.C 2.B 3.A
4.(1)-5s-6t (2)2x2-4xy (3)-1
5.解:(1)原式=9m2-4n2.
(2)原式=a2-b2+a2-4b2=2a2-5b2.
6.解:2x2-18=x2+x2-1+2x,
所以2x=-17,x=-.
7.解:(1)图甲的长是a+b,宽是a-b,面积是(a+b)(a-b)(写成两式乘积形式);如图乙所示,阴影部分的面积是a2-b2(写成多项式的形式).故答案为(a+b),(a-b),(a+b)(a-b),a2-b2.
(2)比较图甲和图乙中阴影部分的面积,可得乘法公式(a+b)(a-b)=a2-b2.故答案为(a+b)(a-b)=a2-b2.
(3)①(x+y)(x-y)=x2-y2;
②(x+3y)(x-3y)=x2-9y2;
③103×97=(100+3)(100-3)=1002-9=9991.
能力巩固作业
8.C
9.x2-1 10.-56 11.-15
12.解:(1)原式=(3n+1)(3n-1)-(3-n)(3+n)
=9n2-1-(9-n2)
=10n2-10.
(2)原式=(m4+16)(m2+4)(m2-4)
=(m4+16)(m4-16)
=m8-256.
素养拓展作业
13.解:因为(a+b)(a-b)=a2-b2,
所以a-b=3,解方程组得
所以a、b的值分别为、.
14.解:因为2×4=(3-1)(3+1)=32-1,3×5=(4-1)(4+1)=42-1,…,所以得出规律(n-1)(n+1)=n2-1(n为大于1的整数).
15.解:(1)(a-b)(a4+a3b+a2b2+ab3+b4)=a5-b5.故答案为a5-b5.
(2)(a-b)(an-1+an-2b+an-3b2+…+abn-2+bn-1)=an-bn.故答案为an-bn.
(3)62019+62018+…+62+6+1=(6-1)(62019+62018+…+62+6)×=.
2
