10.2 平行线的判定 第2课时 课时作业 2023-2024学年初中数学沪科版七年级下册
文档属性
| 名称 | 10.2 平行线的判定 第2课时 课时作业 2023-2024学年初中数学沪科版七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 268.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 09:57:06 | ||
图片预览

文档简介
10.2 平行线的判定
第2课时 同位角相等,两直线平行
【基础达标作业】
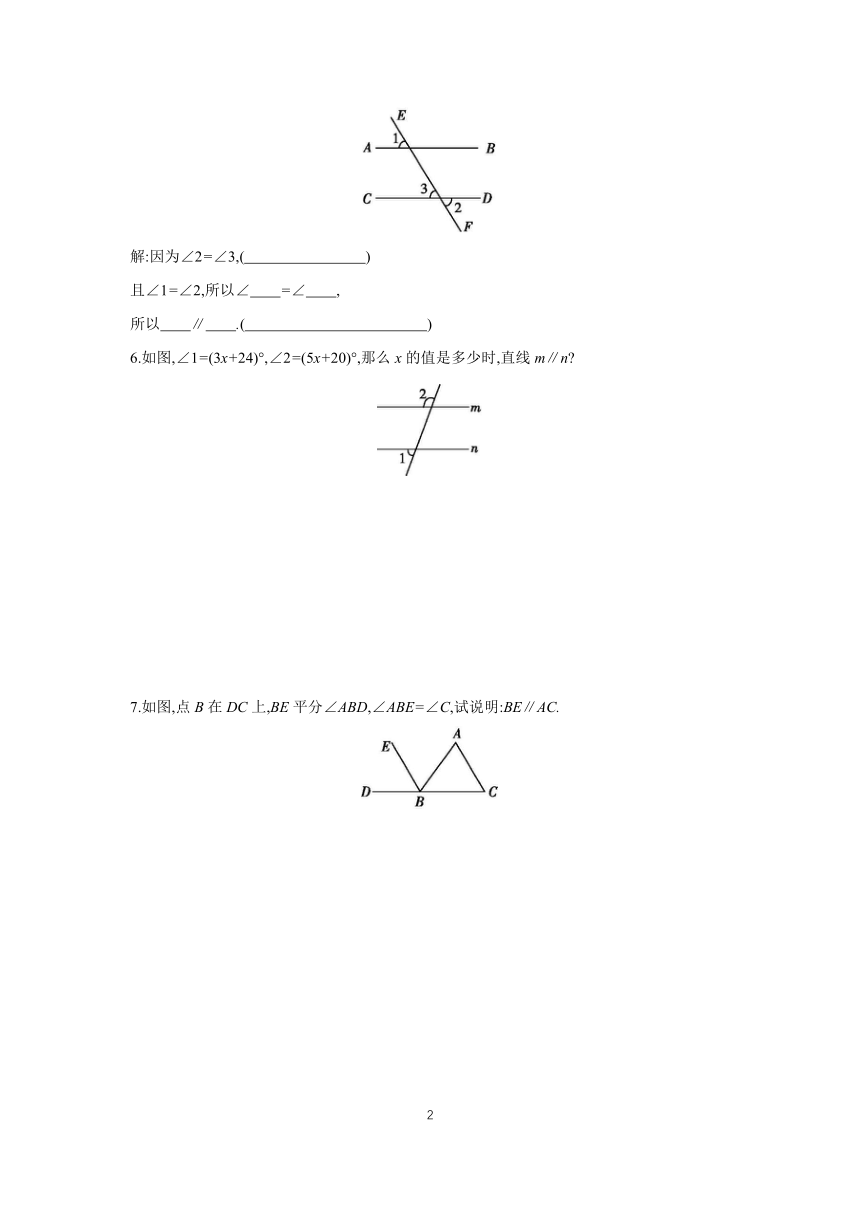
1.如图,直线AB,CD被直线EF所截,要使AB∥CD,则需∠EMB等于 ( )
A.∠AME B.∠BMF
C.∠ENC D.∠END
2.如图,∠C=31°,当∠ABE= 时,BE∥CD.
3.如图,若∠1=∠2,则 AB ∥ ;若∠2= ,则BC∥B'C',理由是 .
4.如图,为了加强房屋的牢固性,要在屋架上加一根栋梁DE,使DE∥BC,如果∠ADE=30°,那么∠ABC= .
5.按图填空,在括号内注明理由.
如图,直线AB、CD被EF所截,∠1=∠2,说明AB平行CD的理由.
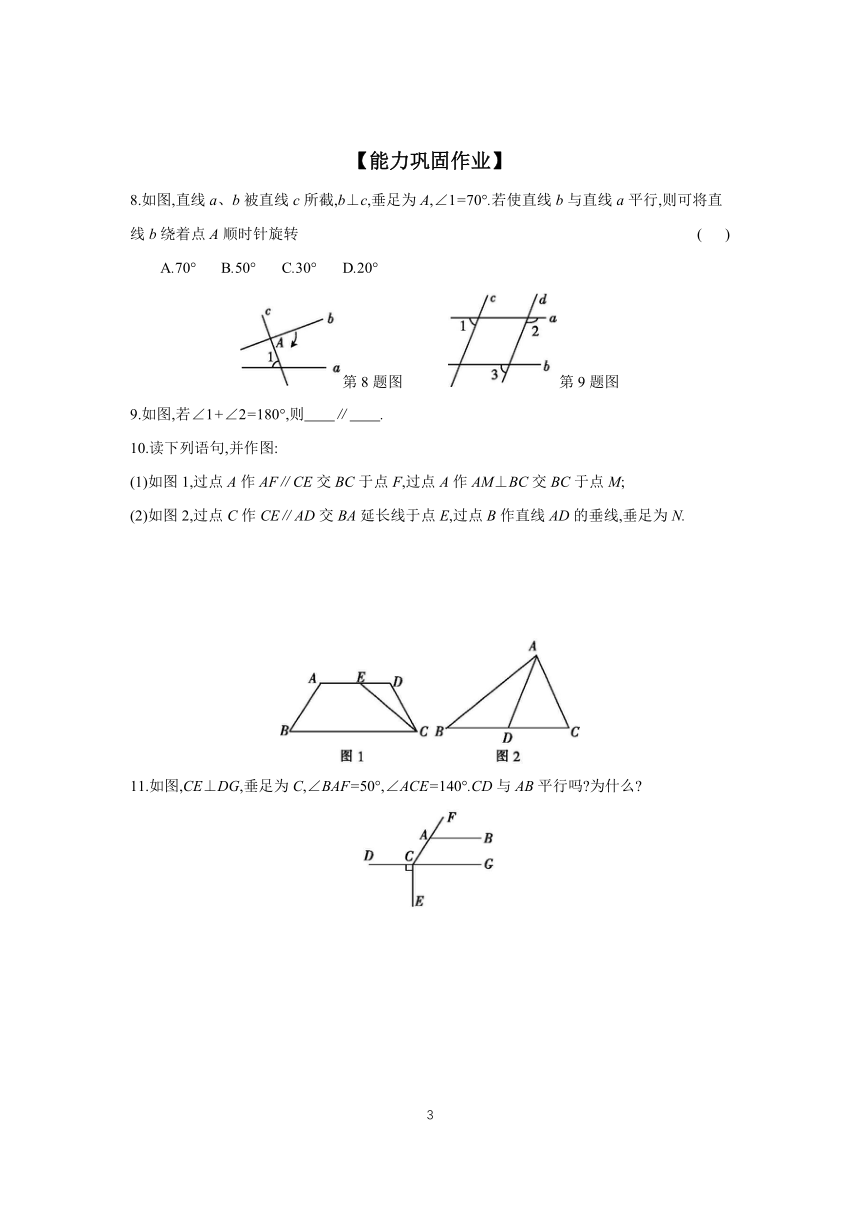
解:因为∠2=∠3,( )
且∠1=∠2,所以∠ =∠ ,
所以 ∥ .( )
6.如图,∠1=(3x+24)°,∠2=(5x+20)°,那么x的值是多少时,直线m∥n
7.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.
【能力巩固作业】
8.如图,直线a、b被直线c所截,b⊥c,垂足为A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转 ( )
A.70° B.50° C.30° D.20°
第8题图 第9题图
9.如图,若∠1+∠2=180°,则 ∥ .
10.读下列语句,并作图:
(1)如图1,过点A作AF∥CE交BC于点F,过点A作AM⊥BC交BC于点M;
(2)如图2,过点C作CE∥AD交BA延长线于点E,过点B作直线AD的垂线,垂足为N.
11.如图,CE⊥DG,垂足为C,∠BAF=50°,∠ACE=140°.CD与AB平行吗 为什么
【素养拓展作业】
12.如图,∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB.试说明:AF∥CE.
解:因为AF平分∠DAB(已知),所以 =∠DAB( ).
因为CE平分∠DCB,所以 =∠DCB( ).
因为∠DAB=∠DCB(已知),所以∠FAE=∠FCE(等量代换).
因为∠FCE=∠CEB(已知),所以∠FAE=∠CEB( ).
所以AF∥CE( ).
13.如图,若∠1=42°,∠2=53°,∠3=85°,则直线l1与l2平行吗 判断并说明理由.
14.如图,DE平分∠BDF,AF平分∠BAC,且∠1=∠2,试说明DF∥AC.
参考答案
基础达标作业
1.D 2.31° 3.A'B' ∠3 同位角相等,两直线平行
4.30°
5.对顶角相等 1 3 AB CD 同位角相等,两直线平行
6.
解:如图,因为∠1+∠3=180°,∠1=(3x+24)°,
所以∠3=180°-(3x+24)°.
又当∠3=∠2=(5x+20)°时,直线m∥n,
所以180°-(3x+24)°=(5x+20)°.
解得x=17.
答:当x=17时,直线m∥n.
7.解:因为BE平分∠ABD,
所以∠DBE=∠ABE.
因为∠ABE=∠C,
所以∠DBE=∠C,
所以BE∥AC.
能力巩固作业
8.D 9.c d
10.解:(1)(2)如图所示:
11.解:平行.
理由:因为CE⊥DG,所以∠ECG=90°,因为∠ACE=140°,所以∠ACG=50°,因为∠BAF=50°,所以∠BAF=∠ACG,所以AB∥DG,即AB∥CD.
素养拓展作业
12.∠FAE 角平分线的定义 ∠FCE 角平分线的定义 等量代换 同位角相等,两直线平行
13.解:直线l1与l2平行.理由:如图,
因为∠2=53°(已知),所以∠4=∠2=53°(对顶角相等).
因为∠3=85°(已知),
所以∠5=180°-∠3-∠4=180°-85°-53°=42°(平角的定义).
因为∠1=42°(已知),所以∠1=∠5(等量代换).
所以l1∥l2(同位角相等,两直线平行).
14.解:因为DE平分∠BDF,AF平分∠BAC,所以∠BDF=2∠1,∠BAC=2∠2.又因为∠1=∠2,所以∠BDF=∠BAC,所以DF∥AC.
2
第2课时 同位角相等,两直线平行
【基础达标作业】
1.如图,直线AB,CD被直线EF所截,要使AB∥CD,则需∠EMB等于 ( )
A.∠AME B.∠BMF
C.∠ENC D.∠END
2.如图,∠C=31°,当∠ABE= 时,BE∥CD.
3.如图,若∠1=∠2,则 AB ∥ ;若∠2= ,则BC∥B'C',理由是 .
4.如图,为了加强房屋的牢固性,要在屋架上加一根栋梁DE,使DE∥BC,如果∠ADE=30°,那么∠ABC= .
5.按图填空,在括号内注明理由.
如图,直线AB、CD被EF所截,∠1=∠2,说明AB平行CD的理由.
解:因为∠2=∠3,( )
且∠1=∠2,所以∠ =∠ ,
所以 ∥ .( )
6.如图,∠1=(3x+24)°,∠2=(5x+20)°,那么x的值是多少时,直线m∥n
7.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.
【能力巩固作业】
8.如图,直线a、b被直线c所截,b⊥c,垂足为A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转 ( )
A.70° B.50° C.30° D.20°
第8题图 第9题图
9.如图,若∠1+∠2=180°,则 ∥ .
10.读下列语句,并作图:
(1)如图1,过点A作AF∥CE交BC于点F,过点A作AM⊥BC交BC于点M;
(2)如图2,过点C作CE∥AD交BA延长线于点E,过点B作直线AD的垂线,垂足为N.
11.如图,CE⊥DG,垂足为C,∠BAF=50°,∠ACE=140°.CD与AB平行吗 为什么
【素养拓展作业】
12.如图,∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB.试说明:AF∥CE.
解:因为AF平分∠DAB(已知),所以 =∠DAB( ).
因为CE平分∠DCB,所以 =∠DCB( ).
因为∠DAB=∠DCB(已知),所以∠FAE=∠FCE(等量代换).
因为∠FCE=∠CEB(已知),所以∠FAE=∠CEB( ).
所以AF∥CE( ).
13.如图,若∠1=42°,∠2=53°,∠3=85°,则直线l1与l2平行吗 判断并说明理由.
14.如图,DE平分∠BDF,AF平分∠BAC,且∠1=∠2,试说明DF∥AC.
参考答案
基础达标作业
1.D 2.31° 3.A'B' ∠3 同位角相等,两直线平行
4.30°
5.对顶角相等 1 3 AB CD 同位角相等,两直线平行
6.
解:如图,因为∠1+∠3=180°,∠1=(3x+24)°,
所以∠3=180°-(3x+24)°.
又当∠3=∠2=(5x+20)°时,直线m∥n,
所以180°-(3x+24)°=(5x+20)°.
解得x=17.
答:当x=17时,直线m∥n.
7.解:因为BE平分∠ABD,
所以∠DBE=∠ABE.
因为∠ABE=∠C,
所以∠DBE=∠C,
所以BE∥AC.
能力巩固作业
8.D 9.c d
10.解:(1)(2)如图所示:
11.解:平行.
理由:因为CE⊥DG,所以∠ECG=90°,因为∠ACE=140°,所以∠ACG=50°,因为∠BAF=50°,所以∠BAF=∠ACG,所以AB∥DG,即AB∥CD.
素养拓展作业
12.∠FAE 角平分线的定义 ∠FCE 角平分线的定义 等量代换 同位角相等,两直线平行
13.解:直线l1与l2平行.理由:如图,
因为∠2=53°(已知),所以∠4=∠2=53°(对顶角相等).
因为∠3=85°(已知),
所以∠5=180°-∠3-∠4=180°-85°-53°=42°(平角的定义).
因为∠1=42°(已知),所以∠1=∠5(等量代换).
所以l1∥l2(同位角相等,两直线平行).
14.解:因为DE平分∠BDF,AF平分∠BAC,所以∠BDF=2∠1,∠BAC=2∠2.又因为∠1=∠2,所以∠BDF=∠BAC,所以DF∥AC.
2
