10.2 平行线的判定 第3课时 课时作业 2023-2024学年初中数学沪科版七年级下册
文档属性
| 名称 | 10.2 平行线的判定 第3课时 课时作业 2023-2024学年初中数学沪科版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 229.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 00:00:00 | ||
图片预览

文档简介
10.2 平行线的判定
第3课时 内错角相等或同旁内角互补,两直线平行
【基础达标作业】
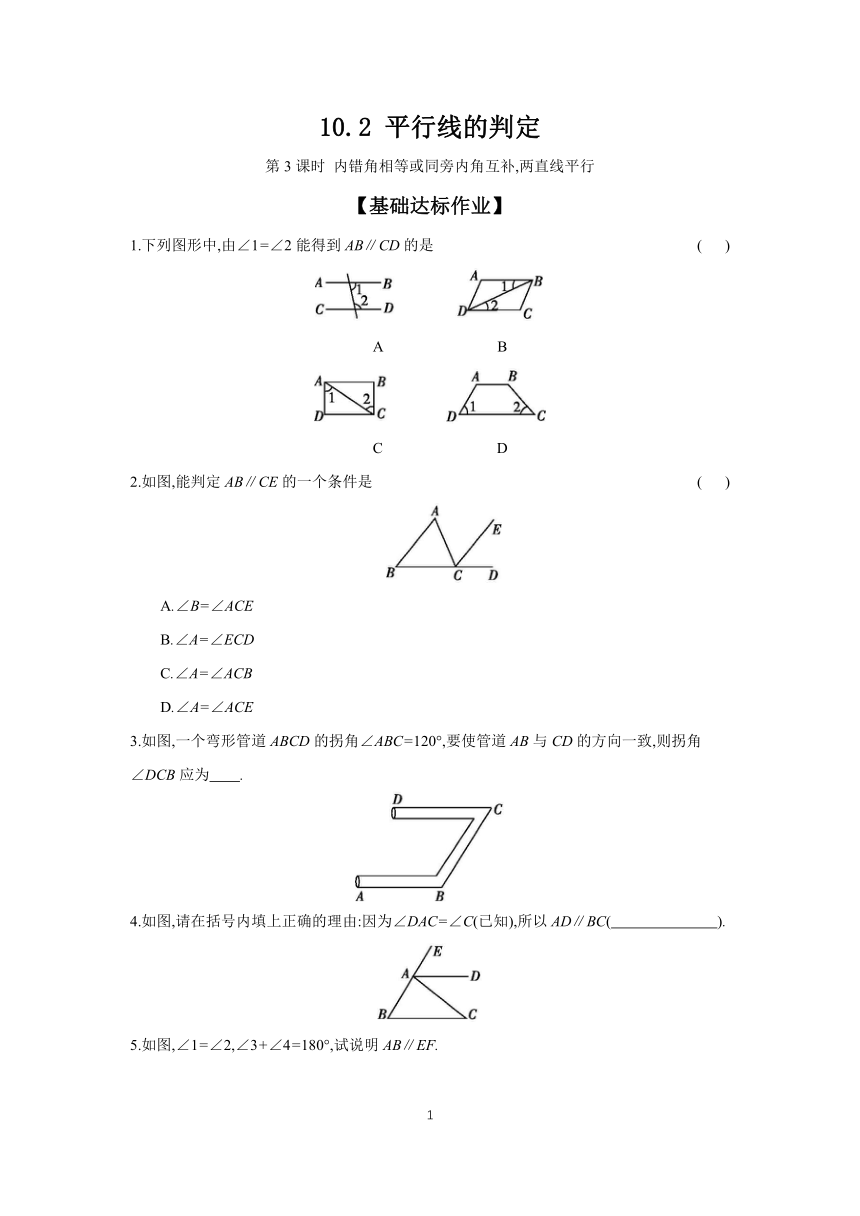
1.下列图形中,由∠1=∠2能得到AB∥CD的是 ( )
A B
C D
2.如图,能判定AB∥CE的一个条件是 ( )
A.∠B=∠ACE
B.∠A=∠ECD
C.∠A=∠ACB
D.∠A=∠ACE
3.如图,一个弯形管道ABCD的拐角∠ABC=120°,要使管道AB与CD的方向一致,则拐角∠DCB应为 .
4.如图,请在括号内填上正确的理由:因为∠DAC=∠C(已知),所以AD∥BC( ).
5.如图,∠1=∠2,∠3+∠4=180°,试说明AB∥EF.
【能力巩固作业】
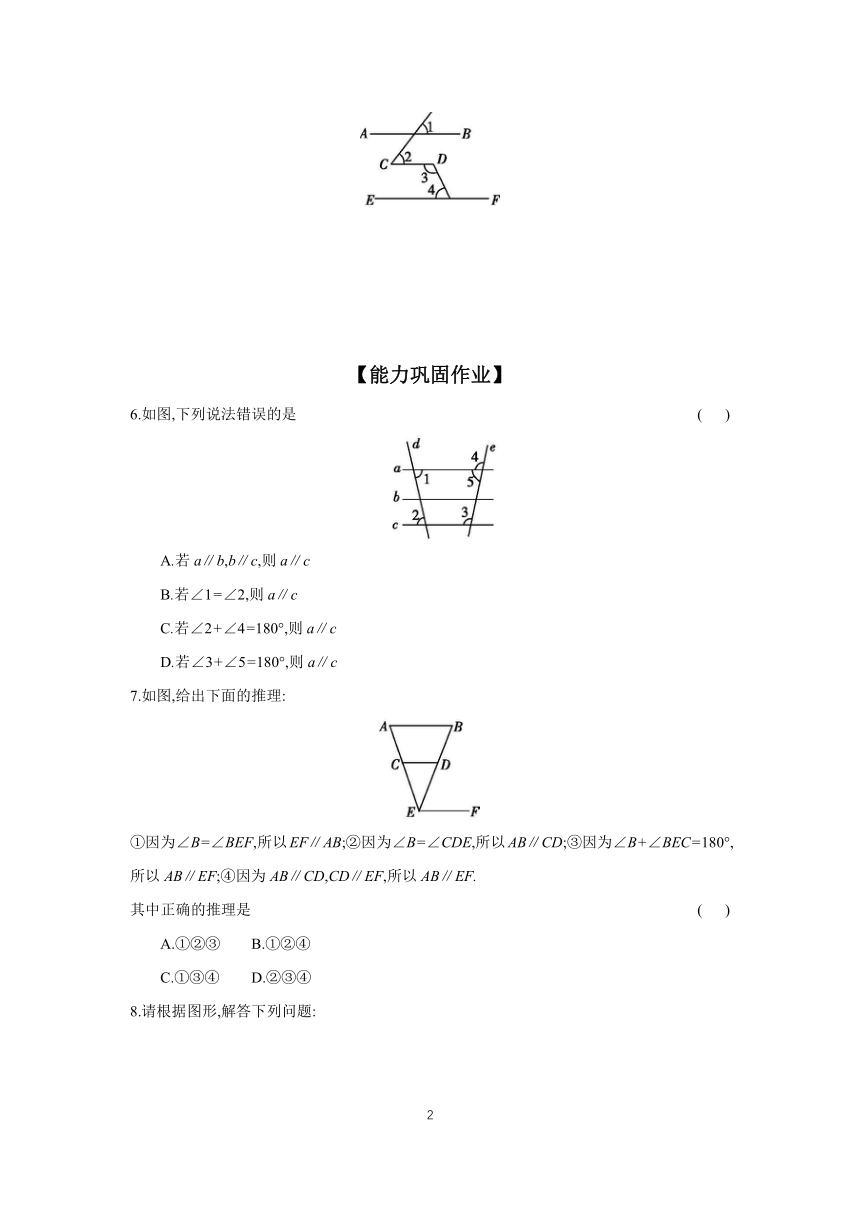
6.如图,下列说法错误的是 ( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠2+∠4=180°,则a∥c
D.若∠3+∠5=180°,则a∥c
7.如图,给出下面的推理:
①因为∠B=∠BEF,所以EF∥AB;②因为∠B=∠CDE,所以AB∥CD;③因为∠B+∠BEC=180°,所以AB∥EF;④因为AB∥CD,CD∥EF,所以AB∥EF.
其中正确的推理是 ( )
A.①②③ B.①②④
C.①③④ D.②③④
8.请根据图形,解答下列问题:
(1)若∠1=∠2,则 ,依据是 ;
(2)若∠3=∠4,则 ,依据是 ;
(3)若∠6=∠7,则 ,依据是 ;
(4)若∠DAB+∠ADC=180°,则 ,依据是 ;
(5)若∠ADC+∠BCD=180°,则 ,依据是 .
9.如图,∠ABC=∠ADC,BE,DF分别是∠ABC,∠ADC的平分线,且∠2=∠3,请说明:BC∥AD.
【素养拓展作业】
10.如图,∠1与∠D互余,CF⊥DF,则AB与CD平行吗 为什么
11.如图,某工程队从点A出发,沿北偏西67°方向铺设管道AD,由于某些原因,BD段不适宜铺设,需改变方向,由B点沿北偏东23°的方向继续铺设BC段,到达C点又改变方向,从C点继续铺设CE段,∠ECB应为多少度,可使所铺管道CE∥AB 试说明理由.此时CE与BC有怎样的位置关系
参考答案
基础达标作业
1.B 2.D 3.60°
4.内错角相等,两直线平行
5.解:因为∠1=∠2,所以AB∥CD.
因为∠3+∠4=180°,所以CD∥EF,
所以AB∥EF.
能力巩固作业
6.C 7.B
8.(1)AD∥BC 内错角相等,两直线平行 (2)AB∥CD 内错角相等,两直线平行 (3)BD∥CF 同位角相等,两直线平行 (4)AB∥CD 同旁内角互补,两直线平行 (5)AD∥BC 同旁内角互补,两直线平行
9.解:因为BE,DF分别是∠ABC和∠ADC的平分线,
所以∠1=∠ABC,∠2=∠ADC.
因为∠ABC=∠ADC,所以∠1=∠2.
因为∠2=∠3,所以∠1=∠3,所以BC∥AD.
素养拓展作业
10.解:AB∥CD.理由:因为CF⊥DF,所以∠CFD=90°.又∠1+∠CFD+∠BFD=180°,所以∠1+∠BFD=90°.又∠1+∠D=90°,所以∠BFD=∠D,所以AB∥CD(内错角相等,两直线平行).
11.解:因为分别过A,B两点的指北方向是平行的,所以∠1=∠A=67°(两直线平行,同位角相等),所以∠CBD=23°+67°=90°,当∠ECB+∠CBD=180°时,CE∥AB(同旁内角互补,两直线平行),所以∠ECB=90°,所以CE⊥BC(垂直定义).
2
第3课时 内错角相等或同旁内角互补,两直线平行
【基础达标作业】
1.下列图形中,由∠1=∠2能得到AB∥CD的是 ( )
A B
C D
2.如图,能判定AB∥CE的一个条件是 ( )
A.∠B=∠ACE
B.∠A=∠ECD
C.∠A=∠ACB
D.∠A=∠ACE
3.如图,一个弯形管道ABCD的拐角∠ABC=120°,要使管道AB与CD的方向一致,则拐角∠DCB应为 .
4.如图,请在括号内填上正确的理由:因为∠DAC=∠C(已知),所以AD∥BC( ).
5.如图,∠1=∠2,∠3+∠4=180°,试说明AB∥EF.
【能力巩固作业】
6.如图,下列说法错误的是 ( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠2+∠4=180°,则a∥c
D.若∠3+∠5=180°,则a∥c
7.如图,给出下面的推理:
①因为∠B=∠BEF,所以EF∥AB;②因为∠B=∠CDE,所以AB∥CD;③因为∠B+∠BEC=180°,所以AB∥EF;④因为AB∥CD,CD∥EF,所以AB∥EF.
其中正确的推理是 ( )
A.①②③ B.①②④
C.①③④ D.②③④
8.请根据图形,解答下列问题:
(1)若∠1=∠2,则 ,依据是 ;
(2)若∠3=∠4,则 ,依据是 ;
(3)若∠6=∠7,则 ,依据是 ;
(4)若∠DAB+∠ADC=180°,则 ,依据是 ;
(5)若∠ADC+∠BCD=180°,则 ,依据是 .
9.如图,∠ABC=∠ADC,BE,DF分别是∠ABC,∠ADC的平分线,且∠2=∠3,请说明:BC∥AD.
【素养拓展作业】
10.如图,∠1与∠D互余,CF⊥DF,则AB与CD平行吗 为什么
11.如图,某工程队从点A出发,沿北偏西67°方向铺设管道AD,由于某些原因,BD段不适宜铺设,需改变方向,由B点沿北偏东23°的方向继续铺设BC段,到达C点又改变方向,从C点继续铺设CE段,∠ECB应为多少度,可使所铺管道CE∥AB 试说明理由.此时CE与BC有怎样的位置关系
参考答案
基础达标作业
1.B 2.D 3.60°
4.内错角相等,两直线平行
5.解:因为∠1=∠2,所以AB∥CD.
因为∠3+∠4=180°,所以CD∥EF,
所以AB∥EF.
能力巩固作业
6.C 7.B
8.(1)AD∥BC 内错角相等,两直线平行 (2)AB∥CD 内错角相等,两直线平行 (3)BD∥CF 同位角相等,两直线平行 (4)AB∥CD 同旁内角互补,两直线平行 (5)AD∥BC 同旁内角互补,两直线平行
9.解:因为BE,DF分别是∠ABC和∠ADC的平分线,
所以∠1=∠ABC,∠2=∠ADC.
因为∠ABC=∠ADC,所以∠1=∠2.
因为∠2=∠3,所以∠1=∠3,所以BC∥AD.
素养拓展作业
10.解:AB∥CD.理由:因为CF⊥DF,所以∠CFD=90°.又∠1+∠CFD+∠BFD=180°,所以∠1+∠BFD=90°.又∠1+∠D=90°,所以∠BFD=∠D,所以AB∥CD(内错角相等,两直线平行).
11.解:因为分别过A,B两点的指北方向是平行的,所以∠1=∠A=67°(两直线平行,同位角相等),所以∠CBD=23°+67°=90°,当∠ECB+∠CBD=180°时,CE∥AB(同旁内角互补,两直线平行),所以∠ECB=90°,所以CE⊥BC(垂直定义).
2
