5.3.1 平行线的性质同步练习(含解析)
文档属性
| 名称 | 5.3.1 平行线的性质同步练习(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 20:22:58 | ||
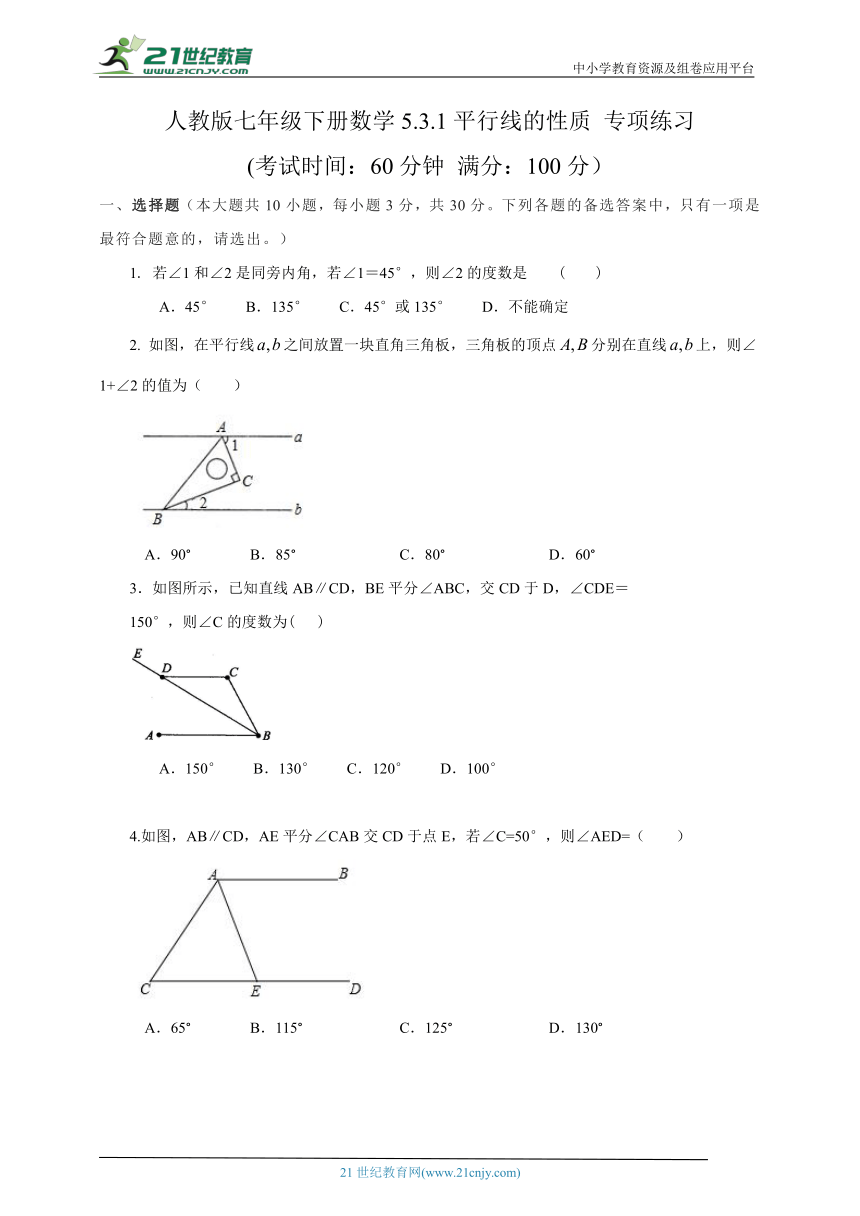
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版七年级下册数学5.3.1平行线的性质 专项练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1. 若∠1和∠2是同旁内角,若∠1=45°,则∠2的度数是 ( )
A.45° B.135° C.45°或135° D.不能确定
如图,在平行线之间放置一块直角三角板,三角板的顶点分别在直线上,则∠1+∠2的值为( )
A.90° B. 85° C. 80° D. 60°
3.如图所示,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=
150°,则∠C的度数为( )
A.150° B.130° C.120° D.100°
4.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
A.65° B.115° C.125° D. 130°
5.如图所示,已知a∥b∥c,∠1=105°,∠2=140°,则∠3的度数是( )
A.75° B.65° C.55° D.50°
6.如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且交EF于点O,则与∠AOE相等的角有( )
A.5个 B.4个 C.3个 D.2个
7.如果两个角的两边分别平行,且其中一个角比另一个角的4倍少,那么这两个角是
A.和 B.都是
C.和或都是 D.以上都不对
8.如图AB∥CD,那么
A.∠1=∠4 B.∠1=∠3
C.∠2=∠3 D.∠1=∠5
9.如图∥,∠=,平分∠,则∠的度数为
A. B.
C. D.
10.小明同学把一个含有角的直角三角板放在如图所示的两条平行线上,测得∠=,则∠的度数是
A. B.
C. D.
二、填空题(本大题共5小题,每小题4分,共20分。)
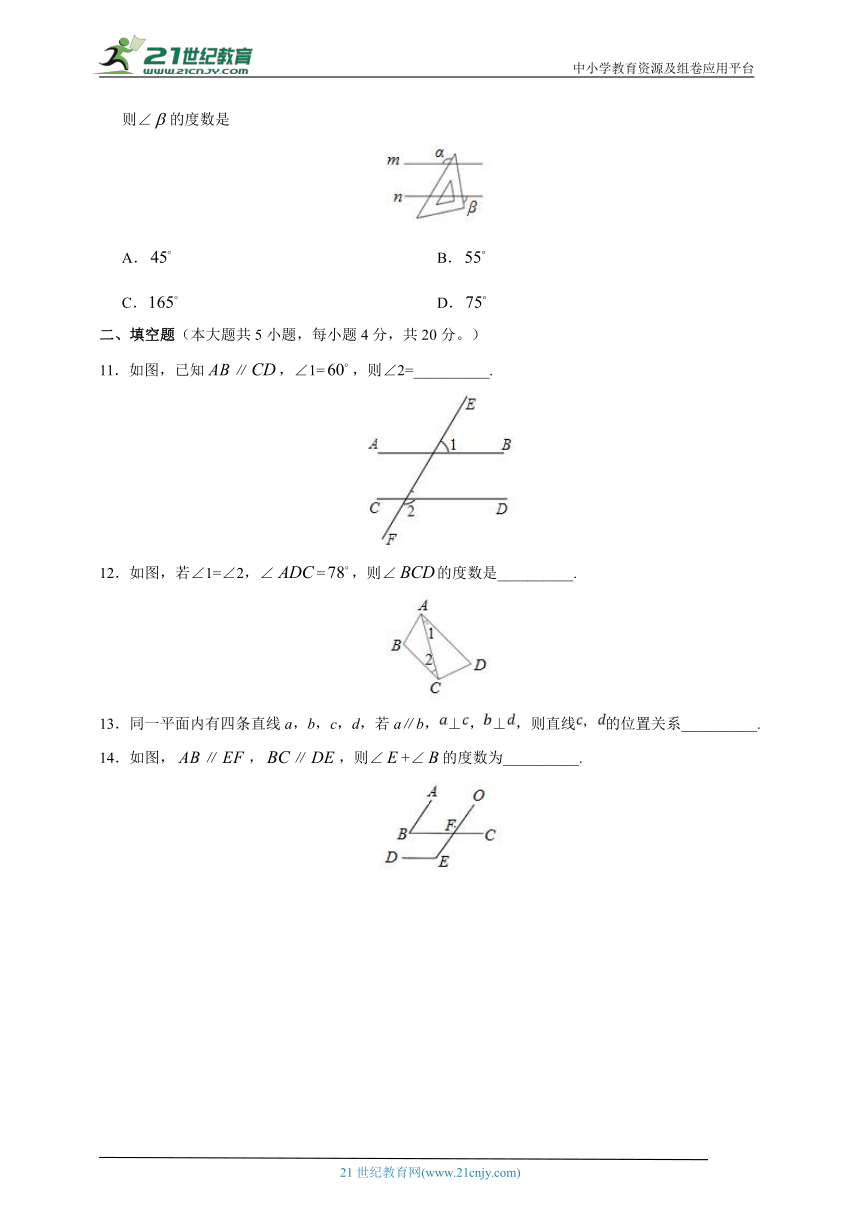
11.如图,已知∥,∠1=,则∠2=__________.
12.如图,若∠1=∠2,∠=,则∠的度数是__________.
13.同一平面内有四条直线a,b,c,d,若a∥b,⊥,⊥,则直线的位置关系__________.
14.如图,∥,∥,则∠+∠的度数为__________.
15.如图所示,直线∥.直线与直线,分别相交于点、点,,垂足为点,若,则= _____,直线之间的距离_____.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,AB∥CD,EF分别交AB、CD与M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数.
17.已知 如图(1),CE∥AB,所以∠1=∠A,∠2=∠B,∴ ∠ACD=∠1+∠2=∠A+∠B.这是一个有用的事实,请用这个结论,在图(2)的四边形ABCD内引一条和边平行的直线,求∠A+∠B+∠C+∠D的度数.
18.如图,AB∥CD,AE,DF分别是∠BAD,∠CDA的平分线,AE与DF平行吗?为什么?
19.如图,是小明设计的智力拼图玩具,现在小明遇到了下面两个问题,请你帮助解决.
(1)如图(1),∠D=,∠ACD=.为保证AB∥DE,∠A应等于多少度?请说明理由;
(2)如图(2),若GP∥HQ,则∠G,∠F,∠H之间有什么样的关系?请说明理由.
20.如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).
一、选择题
1. 【答案】D;
【解析】本题没有给出两条直线平行的条件,因此同旁内角的数量关系是不确定的.
2. 【答案】A.
【解析】过点C作CD∥,则∠1=∠ACD.因∥ ,得CD∥,∴∠2=∠DCB.
又∠ACD+∠DCB=90°,则∠1+∠2=90°.
3. 【答案】C;
【解析】解:如图,
∠3=30°,∠1=∠2=30°,∠C=180°-30°-30°=120°.
4.【答案】B.
【解析】
解:∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠C=50°,
∴∠CAB=180°-50°=130°,
∵AE平分∠CAB,
∴∠EAB=65°,
∵AB∥CD,
∴∠AED=180°﹣∠EAB=180°-65°=115°.
【答案】B
6. 【答案】A
【解析】与∠AOE相等的角有:∠DCA,∠ACB,∠COF,∠CAB,∠DAC.
7.【答案】C
8.【答案】D
【解析】A选项:根据AB∥CD不能推出∠1=∠4,故本选项错误;
B选项:根据AB∥CD不能推出∠1=∠3,故本选项错误;
C选项:根据AB∥CD不能推出∠2=∠3,故本选项错误;
D选项:根据AB∥CD能推出∠1=∠5,故本选项正确;
故选D.
9.【答案】B
10.【答案】D
【解析】如图,
∵m∥n,∴∠1=∠2,
∵∠α=∠2+∠3,而∠3=45°,∠α=120°,
∴∠2=120°–45°=75°,∴∠1=75°,∴∠β=75°.故选D.
填空题
11.答案
12.【答案】
【解析】∵∠1=∠2,∴AD∥BC,∴∠+∠=180°,
又∵∠=,∴∠=(180–78)°=.
故答案是:.
13.【答案】c∥d
【解析】如图:
∵a∥b,a⊥c,∴c⊥b,又∵b⊥d,∴c∥d.故答案是:c∥d.
14.【答案】180°
【解析】∵BC∥DE,∴∠E=∠BFO;∵AB∥EF,∴∠B+∠OFB=180°;∴∠E+∠B=180°.
故答案为:180°.
15.【答案】32°,线段AM的长;
【解析】因为,所以∠ABM=∠1=58°.又因为AM⊥,所以∠2+∠ABM=90°,所以∠2=90°-58°=32°.
解答题
16.【解析】
解:∵∠EMB=50°,
∴∠BMF=180°﹣50°=130°.
∵MG平分∠BMF,
∴∠BMG=∠BMF=65°.
∵AB∥CD,
∴∠MGC=∠BMG=65°.
17.【解析】
解:如图,过点D作DE∥AB交BC于点E.
∴ ∠A+∠2=180°,∠B+∠3=180°(两直线平行,同旁内角互补).
又∵ ∠3=∠1+∠C,
∴ ∠A+∠B+∠C+∠1+∠2=360°,
即∠A+∠B+∠C+∠ADC=360°.
18.
19.
20.
【解析】(1)∠1+∠2=∠3.
理由:过点P作l1的平行线PQ.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版七年级下册数学5.3.1平行线的性质 专项练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1. 若∠1和∠2是同旁内角,若∠1=45°,则∠2的度数是 ( )
A.45° B.135° C.45°或135° D.不能确定
如图,在平行线之间放置一块直角三角板,三角板的顶点分别在直线上,则∠1+∠2的值为( )
A.90° B. 85° C. 80° D. 60°
3.如图所示,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=
150°,则∠C的度数为( )
A.150° B.130° C.120° D.100°
4.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
A.65° B.115° C.125° D. 130°
5.如图所示,已知a∥b∥c,∠1=105°,∠2=140°,则∠3的度数是( )
A.75° B.65° C.55° D.50°
6.如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且交EF于点O,则与∠AOE相等的角有( )
A.5个 B.4个 C.3个 D.2个
7.如果两个角的两边分别平行,且其中一个角比另一个角的4倍少,那么这两个角是
A.和 B.都是
C.和或都是 D.以上都不对
8.如图AB∥CD,那么
A.∠1=∠4 B.∠1=∠3
C.∠2=∠3 D.∠1=∠5
9.如图∥,∠=,平分∠,则∠的度数为
A. B.
C. D.
10.小明同学把一个含有角的直角三角板放在如图所示的两条平行线上,测得∠=,则∠的度数是
A. B.
C. D.
二、填空题(本大题共5小题,每小题4分,共20分。)
11.如图,已知∥,∠1=,则∠2=__________.
12.如图,若∠1=∠2,∠=,则∠的度数是__________.
13.同一平面内有四条直线a,b,c,d,若a∥b,⊥,⊥,则直线的位置关系__________.
14.如图,∥,∥,则∠+∠的度数为__________.
15.如图所示,直线∥.直线与直线,分别相交于点、点,,垂足为点,若,则= _____,直线之间的距离_____.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,AB∥CD,EF分别交AB、CD与M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数.
17.已知 如图(1),CE∥AB,所以∠1=∠A,∠2=∠B,∴ ∠ACD=∠1+∠2=∠A+∠B.这是一个有用的事实,请用这个结论,在图(2)的四边形ABCD内引一条和边平行的直线,求∠A+∠B+∠C+∠D的度数.
18.如图,AB∥CD,AE,DF分别是∠BAD,∠CDA的平分线,AE与DF平行吗?为什么?
19.如图,是小明设计的智力拼图玩具,现在小明遇到了下面两个问题,请你帮助解决.
(1)如图(1),∠D=,∠ACD=.为保证AB∥DE,∠A应等于多少度?请说明理由;
(2)如图(2),若GP∥HQ,则∠G,∠F,∠H之间有什么样的关系?请说明理由.
20.如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).
一、选择题
1. 【答案】D;
【解析】本题没有给出两条直线平行的条件,因此同旁内角的数量关系是不确定的.
2. 【答案】A.
【解析】过点C作CD∥,则∠1=∠ACD.因∥ ,得CD∥,∴∠2=∠DCB.
又∠ACD+∠DCB=90°,则∠1+∠2=90°.
3. 【答案】C;
【解析】解:如图,
∠3=30°,∠1=∠2=30°,∠C=180°-30°-30°=120°.
4.【答案】B.
【解析】
解:∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠C=50°,
∴∠CAB=180°-50°=130°,
∵AE平分∠CAB,
∴∠EAB=65°,
∵AB∥CD,
∴∠AED=180°﹣∠EAB=180°-65°=115°.
【答案】B
6. 【答案】A
【解析】与∠AOE相等的角有:∠DCA,∠ACB,∠COF,∠CAB,∠DAC.
7.【答案】C
8.【答案】D
【解析】A选项:根据AB∥CD不能推出∠1=∠4,故本选项错误;
B选项:根据AB∥CD不能推出∠1=∠3,故本选项错误;
C选项:根据AB∥CD不能推出∠2=∠3,故本选项错误;
D选项:根据AB∥CD能推出∠1=∠5,故本选项正确;
故选D.
9.【答案】B
10.【答案】D
【解析】如图,
∵m∥n,∴∠1=∠2,
∵∠α=∠2+∠3,而∠3=45°,∠α=120°,
∴∠2=120°–45°=75°,∴∠1=75°,∴∠β=75°.故选D.
填空题
11.答案
12.【答案】
【解析】∵∠1=∠2,∴AD∥BC,∴∠+∠=180°,
又∵∠=,∴∠=(180–78)°=.
故答案是:.
13.【答案】c∥d
【解析】如图:
∵a∥b,a⊥c,∴c⊥b,又∵b⊥d,∴c∥d.故答案是:c∥d.
14.【答案】180°
【解析】∵BC∥DE,∴∠E=∠BFO;∵AB∥EF,∴∠B+∠OFB=180°;∴∠E+∠B=180°.
故答案为:180°.
15.【答案】32°,线段AM的长;
【解析】因为,所以∠ABM=∠1=58°.又因为AM⊥,所以∠2+∠ABM=90°,所以∠2=90°-58°=32°.
解答题
16.【解析】
解:∵∠EMB=50°,
∴∠BMF=180°﹣50°=130°.
∵MG平分∠BMF,
∴∠BMG=∠BMF=65°.
∵AB∥CD,
∴∠MGC=∠BMG=65°.
17.【解析】
解:如图,过点D作DE∥AB交BC于点E.
∴ ∠A+∠2=180°,∠B+∠3=180°(两直线平行,同旁内角互补).
又∵ ∠3=∠1+∠C,
∴ ∠A+∠B+∠C+∠1+∠2=360°,
即∠A+∠B+∠C+∠ADC=360°.
18.
19.
20.
【解析】(1)∠1+∠2=∠3.
理由:过点P作l1的平行线PQ.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
