2023-2024学年初中数学人教版七年级下册5.1.1 相交线 分层作业 (含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版七年级下册5.1.1 相交线 分层作业 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 165.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 00:00:00 | ||
图片预览

文档简介
5.1.1 相交线
【练基础】
必备知识1 对顶角定义、性质
1.【教材P7习题5.1T1变式】【张家口期末】下列四个图形中,∠1与∠2互为对顶角的是( )
A B C D
2.如图,直线a,b相交于点O,若∠1=40°,则∠2=( )
A.40° B.50° C.60° D.140°
3.【石家庄期末】如图,直线a,b相交于点O,将半圆形量角器的圆心与点O重合,发现表示60°的刻度与直线a重合,表示138°的刻度与直线b重合,则∠1的度数为____________.
4.【张家口期中】如图,AB,CD,EF相交于点O,∠1=35°,∠2=35°,则∠3的度数是______________.
必备知识2 邻补角定义、性质
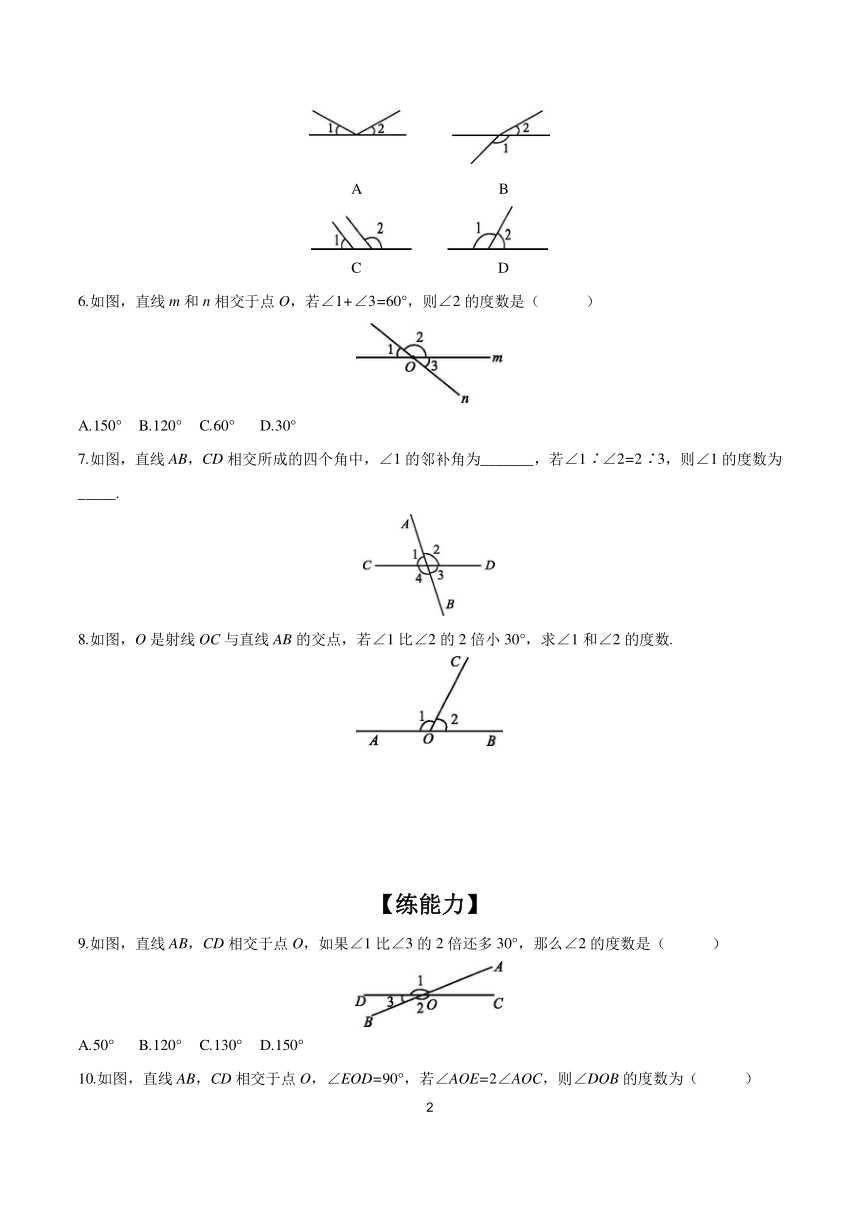
5.下列图形中,∠1与∠2互为邻补角的是( )
A B
C D
6.如图,直线m和n相交于点O,若∠1+∠3=60°,则∠2的度数是( )
A.150° B.120° C.60° D.30°
7.如图,直线AB,CD相交所成的四个角中,∠1的邻补角为_______,若∠1∶∠2=2∶3,则∠1的度数为_____.
8.如图,O是射线OC与直线AB的交点,若∠1比∠2的2倍小30°,求∠1和∠2的度数.
【练能力】
9.如图,直线AB,CD相交于点O,如果∠1比∠3的2倍还多30°,那么∠2的度数是( )
A.50° B.120° C.130° D.150°
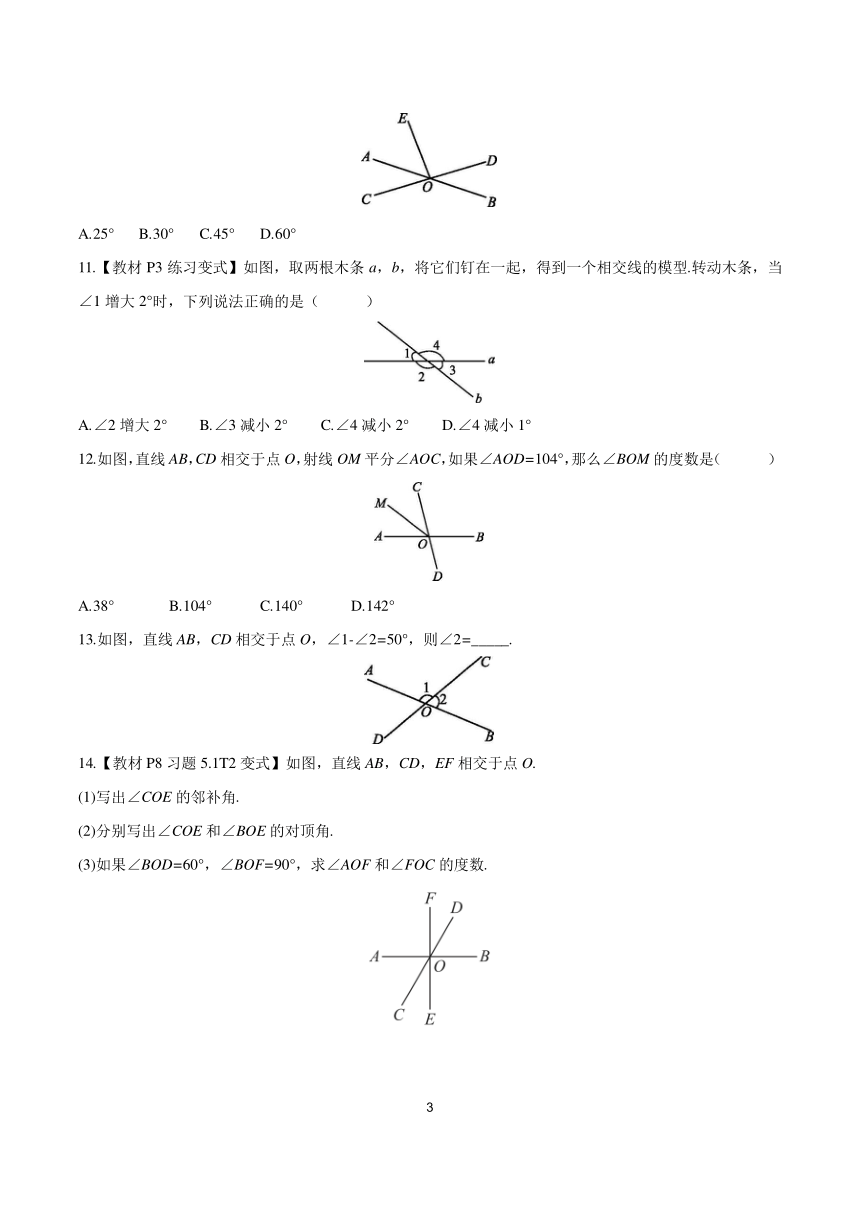
10.如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )
A.25° B.30° C.45° D.60°
11.【教材P3练习变式】如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型.转动木条,当∠1增大2°时,下列说法正确的是( )
A.∠2增大2° B.∠3减小2° C.∠4减小2° D.∠4减小1°
12.如图,直线AB,CD相交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM的度数是( )
A.38° B.104° C.140° D.142°
13.如图,直线AB,CD相交于点O,∠1-∠2=50°,则∠2=_____.
14.【教材P8习题5.1T2变式】如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角.
(2)分别写出∠COE和∠BOE的对顶角.
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
【练素养】
15.通过画图,寻找对顶角和邻补角(不含平角):
(1)若2条直线相交于一点,则有____对对顶角,____对邻补角.
(2)若3条直线相交于同一点,则有____对对顶角,____对邻补角.
(3)若4条直线相交于同一点,则有____对对顶角,____对邻补角.
(4)通过(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于同一点,则可形成____对对顶角,____对邻补角.
16.如图,直线AB,CD相交于点O,已知∠BOC=75°,ON将∠AOD分成两个角,且∠AON∶∠NOD=2∶3.
(1)求∠AON的度数.
(2)若OM平分∠BON,则OB是∠COM的平分线吗 判断并说明理由.
参考答案
【练基础】
1.C 2.A
3.78°
4.110°
5.D 6.A
7.∠2和∠4 72°
8.【解析】设∠2=x,则∠1=2x-30°.
因为∠1+∠2=180°,所以2x-30°+x=180°,
解得x=70°,
所以∠1=110°,∠2=70°.
【练能力】
9.C 10.B 11.C
12.D 【解析】解法一 因为∠AOD=104°,所以∠AOC=180°-104°=76°,∠BOC=∠AOD=104°.因为射线OM平分∠AOC,所以∠COM=∠AOC=38°,所以∠BOM=∠BOC+∠COM=104°+38°=142°.
解法二 因为∠AOD=104°,所以∠AOC=180°-104°=76°.因为射线OM平分∠AOC,所以∠AOM=∠AOC=38°,所以∠BOM=180°-∠AOM=180°-38°=142°.
13.65°
14.【解析】(1)∠COE的邻补角为∠COF和∠EOD.
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF.
(3)因为∠BOF=90°,
所以∠AOF=180°-∠BOF=90°.
因为∠BOD=60°,所以∠AOC=∠BOD=60°,
所以∠FOC=∠AOF+∠AOC=90°+60°=150°.
【练素养】
15.【解析】由画图可知,
(1)2,4.(2)6,12.(3)12,24.
(4)n(n-1),2n(n-1).
16.【解析】(1)设∠AON=2x,则∠NOD=3x,
所以∠AOD=5x.
因为∠BOC=75°,所以∠AOD=5x=75°,
所以x=15°,所以∠AON=30°.
(2)OB是∠COM的平分线.
理由:因为∠AON=30°,
所以∠BON=180°-∠AON=150°.
因为OM平分∠BON,所以∠BOM=75°,
所以∠BOM=∠BOC,
所以OB是∠COM的平分线.
2
【练基础】
必备知识1 对顶角定义、性质
1.【教材P7习题5.1T1变式】【张家口期末】下列四个图形中,∠1与∠2互为对顶角的是( )
A B C D
2.如图,直线a,b相交于点O,若∠1=40°,则∠2=( )
A.40° B.50° C.60° D.140°
3.【石家庄期末】如图,直线a,b相交于点O,将半圆形量角器的圆心与点O重合,发现表示60°的刻度与直线a重合,表示138°的刻度与直线b重合,则∠1的度数为____________.
4.【张家口期中】如图,AB,CD,EF相交于点O,∠1=35°,∠2=35°,则∠3的度数是______________.
必备知识2 邻补角定义、性质
5.下列图形中,∠1与∠2互为邻补角的是( )
A B
C D
6.如图,直线m和n相交于点O,若∠1+∠3=60°,则∠2的度数是( )
A.150° B.120° C.60° D.30°
7.如图,直线AB,CD相交所成的四个角中,∠1的邻补角为_______,若∠1∶∠2=2∶3,则∠1的度数为_____.
8.如图,O是射线OC与直线AB的交点,若∠1比∠2的2倍小30°,求∠1和∠2的度数.
【练能力】
9.如图,直线AB,CD相交于点O,如果∠1比∠3的2倍还多30°,那么∠2的度数是( )
A.50° B.120° C.130° D.150°
10.如图,直线AB,CD相交于点O,∠EOD=90°,若∠AOE=2∠AOC,则∠DOB的度数为( )
A.25° B.30° C.45° D.60°
11.【教材P3练习变式】如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型.转动木条,当∠1增大2°时,下列说法正确的是( )
A.∠2增大2° B.∠3减小2° C.∠4减小2° D.∠4减小1°
12.如图,直线AB,CD相交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM的度数是( )
A.38° B.104° C.140° D.142°
13.如图,直线AB,CD相交于点O,∠1-∠2=50°,则∠2=_____.
14.【教材P8习题5.1T2变式】如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角.
(2)分别写出∠COE和∠BOE的对顶角.
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
【练素养】
15.通过画图,寻找对顶角和邻补角(不含平角):
(1)若2条直线相交于一点,则有____对对顶角,____对邻补角.
(2)若3条直线相交于同一点,则有____对对顶角,____对邻补角.
(3)若4条直线相交于同一点,则有____对对顶角,____对邻补角.
(4)通过(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于同一点,则可形成____对对顶角,____对邻补角.
16.如图,直线AB,CD相交于点O,已知∠BOC=75°,ON将∠AOD分成两个角,且∠AON∶∠NOD=2∶3.
(1)求∠AON的度数.
(2)若OM平分∠BON,则OB是∠COM的平分线吗 判断并说明理由.
参考答案
【练基础】
1.C 2.A
3.78°
4.110°
5.D 6.A
7.∠2和∠4 72°
8.【解析】设∠2=x,则∠1=2x-30°.
因为∠1+∠2=180°,所以2x-30°+x=180°,
解得x=70°,
所以∠1=110°,∠2=70°.
【练能力】
9.C 10.B 11.C
12.D 【解析】解法一 因为∠AOD=104°,所以∠AOC=180°-104°=76°,∠BOC=∠AOD=104°.因为射线OM平分∠AOC,所以∠COM=∠AOC=38°,所以∠BOM=∠BOC+∠COM=104°+38°=142°.
解法二 因为∠AOD=104°,所以∠AOC=180°-104°=76°.因为射线OM平分∠AOC,所以∠AOM=∠AOC=38°,所以∠BOM=180°-∠AOM=180°-38°=142°.
13.65°
14.【解析】(1)∠COE的邻补角为∠COF和∠EOD.
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF.
(3)因为∠BOF=90°,
所以∠AOF=180°-∠BOF=90°.
因为∠BOD=60°,所以∠AOC=∠BOD=60°,
所以∠FOC=∠AOF+∠AOC=90°+60°=150°.
【练素养】
15.【解析】由画图可知,
(1)2,4.(2)6,12.(3)12,24.
(4)n(n-1),2n(n-1).
16.【解析】(1)设∠AON=2x,则∠NOD=3x,
所以∠AOD=5x.
因为∠BOC=75°,所以∠AOD=5x=75°,
所以x=15°,所以∠AON=30°.
(2)OB是∠COM的平分线.
理由:因为∠AON=30°,
所以∠BON=180°-∠AON=150°.
因为OM平分∠BON,所以∠BOM=75°,
所以∠BOM=∠BOC,
所以OB是∠COM的平分线.
2
