2023-2024学年初中数学人教版七年级下册5.1.2.1 垂线 分层作业(含解析)
文档属性
| 名称 | 2023-2024学年初中数学人教版七年级下册5.1.2.1 垂线 分层作业(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 195.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 15:32:38 | ||
图片预览


文档简介
5.1.2.1垂线
【练基础】
必备知识1 垂直定义
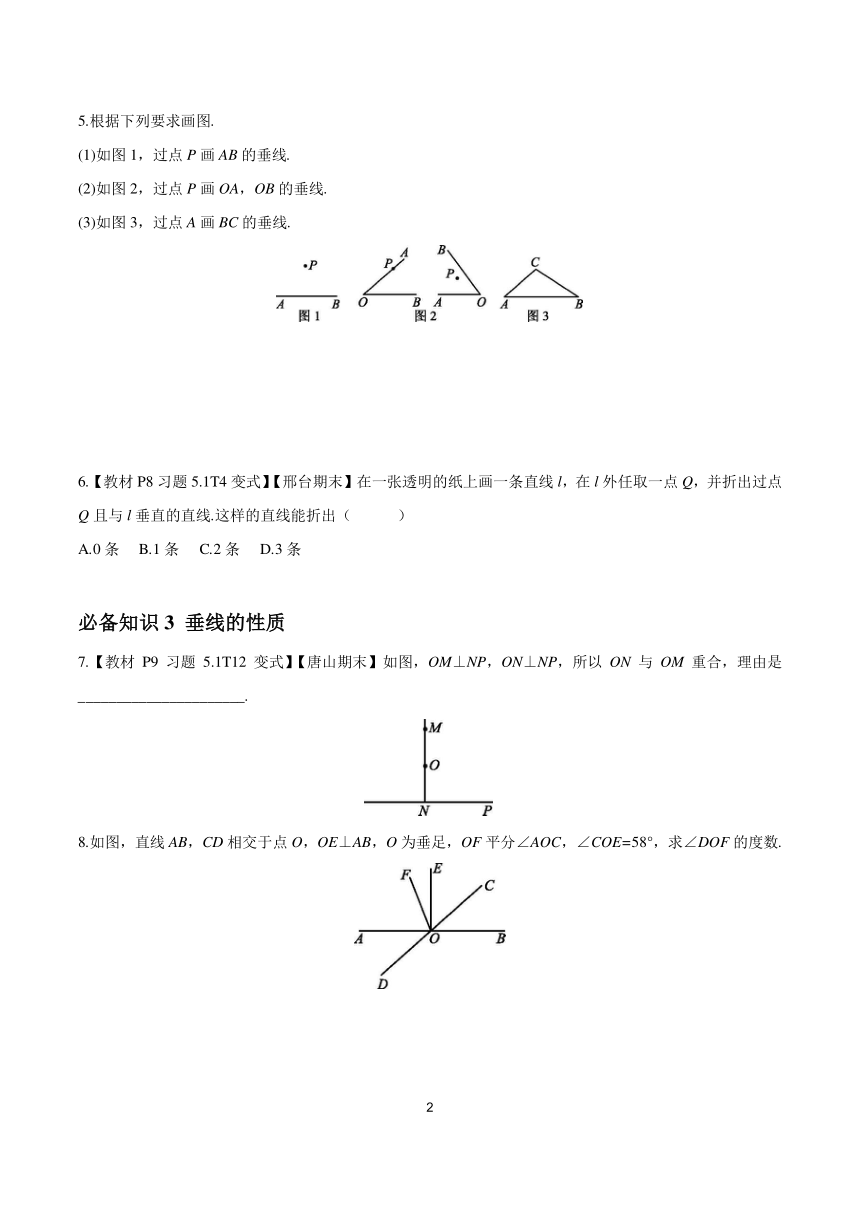
1.如图,OA⊥OB,若∠1=35°,则∠2的度数为( )
A.35° B.45° C.55° D.70°
2.如图,点O在直线AB上,OC⊥OD.若∠AOC=120°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
3.【沧州期中】如图,直线AB,CD相交于点O,OM⊥AB,垂足为O.
(1)若∠1=∠2,求∠NOD的度数.
(2)若∠AOD=4∠1,求∠AOC和∠MOD的度数.
必备知识2 垂线的画法
4.下列选项中,过点P画AB的垂线CD,三角板放法正确的是( )
A B C D
5.根据下列要求画图.
(1)如图1,过点P画AB的垂线.
(2)如图2,过点P画OA,OB的垂线.
(3)如图3,过点A画BC的垂线.
6.【教材P8习题5.1T4变式】【邢台期末】在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线.这样的直线能折出( )
A.0条 B.1条 C.2条 D.3条
必备知识3 垂线的性质
7.【教材P9习题5.1T12变式】【唐山期末】如图,OM⊥NP,ON⊥NP,所以ON与OM重合,理由是______________________.
8.如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,OF平分∠AOC,∠COE=58°,求∠DOF的度数.
【练能力】
9.【唐山期末】如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF,则∠GEB的度数为( )
A.10° B.20° C.30° D.40°
10.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,其中正确的是( )
A B C D
11.已知OA⊥OC,∠AOB∶∠BOC=1∶4,则∠BOC的度数为( )
A.54° B.54°或120°·C.72°或120° D.54°或72°
12.如图,已知AO⊥OB,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化 说明理由.
(2)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.
13. 【六安期末】如图,直线AB,CD相交于点O,且OE⊥AB.
(1)过点O画CD的垂线MN.
(2)若F是(1)中所画直线MN上任意一点(点O除外),且∠AOC=34°,求∠EOF的度数.
【练素养】
14.如图,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM,ON分别是∠AOC,∠BOD的平分线.
(1)猜想OC与OD的位置关系,并说明理由.
(2)求∠MON的度数.
(3)若只改变∠AOC和∠BOD的度数,其他条件不变,则∠AOM+∠BON与∠AOC+∠BOD有什么样的数量关系 请直接写出结论.
参考答案
【练基础】
1.C 2.A
3.【解析】(1)因为OM⊥AB,所以∠AOM=90°,
即∠AOC+∠1=90°.
因为∠1=∠2,
所以∠AOC+∠2=90°,即∠NOC=90°,
所以∠NOD=180°-∠NOC=180°-90°=90°.
(2)由(1)知∠AOC+∠1=90°,
所以∠AOC=90°-∠1.
因为∠AOC+∠AOD=180°,∠AOD=4∠1,
所以90°-∠1+4∠1=180°,解得∠1=30°,
所以∠AOC=90°-∠1=90°-30°=60°,
∠MOD=180°-∠1=180°-30°=150°.
4.C
5.【解析】(1)如图1所示.
(2)如图2所示.
(3)如图3所示.
6.B
7.在同一平面内,过一点有且只有一条直线与已知直线垂直
8.【解析】因为OE⊥AB,
所以∠AOE=∠BOE=90°.
因为∠COE=58°,
所以∠BOC=32°,∠AOC=∠AOE+∠COE=148°.
因为OF平分∠AOC,
所以∠AOF=∠AOC=74°.
因为∠BOC=∠AOD,
所以∠DOF=∠AOD+∠AOF=32°+74°=106°.
【练能力】
9.B 10.A
11.C 【解析】因为OA⊥OC,所以∠AOC=90°.如图1,因为∠AOB∶∠BOC=1∶4,所以∠BOC=∠AOC=72°;如图2,因为∠AOB∶∠BOC=1∶4,所以∠BOC∶∠AOC=4∶3,所以∠BOC=∠AOC=120°.综上所述,∠BOC的度数为72°或120°.
12.【解析】(1)∠DOE的大小不变.理由如下:
因为AO⊥OB,所以∠AOB=90°.
因为OD,OE分别平分∠AOC和∠BOC,
所以∠COD=∠AOC,∠COE=∠BOC,
所以∠DOE=∠COD+∠COE=∠AOC+∠COB=(∠AOC+∠COB)=∠AOB=45°,
所以∠DOE的大小不变.
(2)如图1,∠DOE的度数为45°;
如图2,∠DOE的度数为135°.
13.【解析】(1)如图1所示.
(2)①如图2,当点F在射线OM上时,
因为EO⊥AB,MN⊥CD,
所以∠AOE=∠COM=90°,
所以∠MOE+∠AOM=90°,∠AOM+∠AOC=90°,
所以∠EOF=∠AOC=34°.
②如图2,当点F在射线ON上时,
因为OE⊥AB,所以∠EOB=90°.
因为MN⊥CD,所以∠MOC=∠AOC+∠AOM=90°,
所以∠AOM=90°-∠AOC=56°,
所以∠BON=∠AOM=56°,
所以∠EOF=∠EOB+∠BON=90°+56°=146°.
综上所述,∠EOF的度数是34°或146°.
【练素养】
14.【解析】(1)OC与OD垂直.
理由:因为∠AOB是平角,∠AOC=30°,∠BOD=60°,
所以∠COD=∠AOB-∠AOC-∠BOD=180°-30°-60°=90°.
故OC与OD垂直.
(2)因为OM,ON分别是∠AOC,∠BOD的平分线,
所以∠COM=∠AOC=15°,∠DON=∠BOD=30°,
所以∠MON=∠COM+∠COD+∠DON=15°+90°+30°=135°,
即∠MON的度数为135°.
(3)∠AOM+∠BON=(∠AOC+∠BOD).
提示:因为OM,ON分别是∠AOC,∠BOD的平分线,
所以∠AOM=∠AOC,∠BON=∠BOD,
所以∠AOM+∠BON=∠AOC+∠BOD=(∠AOC+∠BOD).
2
【练基础】
必备知识1 垂直定义
1.如图,OA⊥OB,若∠1=35°,则∠2的度数为( )
A.35° B.45° C.55° D.70°
2.如图,点O在直线AB上,OC⊥OD.若∠AOC=120°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
3.【沧州期中】如图,直线AB,CD相交于点O,OM⊥AB,垂足为O.
(1)若∠1=∠2,求∠NOD的度数.
(2)若∠AOD=4∠1,求∠AOC和∠MOD的度数.
必备知识2 垂线的画法
4.下列选项中,过点P画AB的垂线CD,三角板放法正确的是( )
A B C D
5.根据下列要求画图.
(1)如图1,过点P画AB的垂线.
(2)如图2,过点P画OA,OB的垂线.
(3)如图3,过点A画BC的垂线.
6.【教材P8习题5.1T4变式】【邢台期末】在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线.这样的直线能折出( )
A.0条 B.1条 C.2条 D.3条
必备知识3 垂线的性质
7.【教材P9习题5.1T12变式】【唐山期末】如图,OM⊥NP,ON⊥NP,所以ON与OM重合,理由是______________________.
8.如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,OF平分∠AOC,∠COE=58°,求∠DOF的度数.
【练能力】
9.【唐山期末】如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF,则∠GEB的度数为( )
A.10° B.20° C.30° D.40°
10.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,其中正确的是( )
A B C D
11.已知OA⊥OC,∠AOB∶∠BOC=1∶4,则∠BOC的度数为( )
A.54° B.54°或120°·C.72°或120° D.54°或72°
12.如图,已知AO⊥OB,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化 说明理由.
(2)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.
13. 【六安期末】如图,直线AB,CD相交于点O,且OE⊥AB.
(1)过点O画CD的垂线MN.
(2)若F是(1)中所画直线MN上任意一点(点O除外),且∠AOC=34°,求∠EOF的度数.
【练素养】
14.如图,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM,ON分别是∠AOC,∠BOD的平分线.
(1)猜想OC与OD的位置关系,并说明理由.
(2)求∠MON的度数.
(3)若只改变∠AOC和∠BOD的度数,其他条件不变,则∠AOM+∠BON与∠AOC+∠BOD有什么样的数量关系 请直接写出结论.
参考答案
【练基础】
1.C 2.A
3.【解析】(1)因为OM⊥AB,所以∠AOM=90°,
即∠AOC+∠1=90°.
因为∠1=∠2,
所以∠AOC+∠2=90°,即∠NOC=90°,
所以∠NOD=180°-∠NOC=180°-90°=90°.
(2)由(1)知∠AOC+∠1=90°,
所以∠AOC=90°-∠1.
因为∠AOC+∠AOD=180°,∠AOD=4∠1,
所以90°-∠1+4∠1=180°,解得∠1=30°,
所以∠AOC=90°-∠1=90°-30°=60°,
∠MOD=180°-∠1=180°-30°=150°.
4.C
5.【解析】(1)如图1所示.
(2)如图2所示.
(3)如图3所示.
6.B
7.在同一平面内,过一点有且只有一条直线与已知直线垂直
8.【解析】因为OE⊥AB,
所以∠AOE=∠BOE=90°.
因为∠COE=58°,
所以∠BOC=32°,∠AOC=∠AOE+∠COE=148°.
因为OF平分∠AOC,
所以∠AOF=∠AOC=74°.
因为∠BOC=∠AOD,
所以∠DOF=∠AOD+∠AOF=32°+74°=106°.
【练能力】
9.B 10.A
11.C 【解析】因为OA⊥OC,所以∠AOC=90°.如图1,因为∠AOB∶∠BOC=1∶4,所以∠BOC=∠AOC=72°;如图2,因为∠AOB∶∠BOC=1∶4,所以∠BOC∶∠AOC=4∶3,所以∠BOC=∠AOC=120°.综上所述,∠BOC的度数为72°或120°.
12.【解析】(1)∠DOE的大小不变.理由如下:
因为AO⊥OB,所以∠AOB=90°.
因为OD,OE分别平分∠AOC和∠BOC,
所以∠COD=∠AOC,∠COE=∠BOC,
所以∠DOE=∠COD+∠COE=∠AOC+∠COB=(∠AOC+∠COB)=∠AOB=45°,
所以∠DOE的大小不变.
(2)如图1,∠DOE的度数为45°;
如图2,∠DOE的度数为135°.
13.【解析】(1)如图1所示.
(2)①如图2,当点F在射线OM上时,
因为EO⊥AB,MN⊥CD,
所以∠AOE=∠COM=90°,
所以∠MOE+∠AOM=90°,∠AOM+∠AOC=90°,
所以∠EOF=∠AOC=34°.
②如图2,当点F在射线ON上时,
因为OE⊥AB,所以∠EOB=90°.
因为MN⊥CD,所以∠MOC=∠AOC+∠AOM=90°,
所以∠AOM=90°-∠AOC=56°,
所以∠BON=∠AOM=56°,
所以∠EOF=∠EOB+∠BON=90°+56°=146°.
综上所述,∠EOF的度数是34°或146°.
【练素养】
14.【解析】(1)OC与OD垂直.
理由:因为∠AOB是平角,∠AOC=30°,∠BOD=60°,
所以∠COD=∠AOB-∠AOC-∠BOD=180°-30°-60°=90°.
故OC与OD垂直.
(2)因为OM,ON分别是∠AOC,∠BOD的平分线,
所以∠COM=∠AOC=15°,∠DON=∠BOD=30°,
所以∠MON=∠COM+∠COD+∠DON=15°+90°+30°=135°,
即∠MON的度数为135°.
(3)∠AOM+∠BON=(∠AOC+∠BOD).
提示:因为OM,ON分别是∠AOC,∠BOD的平分线,
所以∠AOM=∠AOC,∠BON=∠BOD,
所以∠AOM+∠BON=∠AOC+∠BOD=(∠AOC+∠BOD).
2
