5.2.2 平行线的判定 分层作业(含答案) 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 5.2.2 平行线的判定 分层作业(含答案) 2023-2024学年初中数学人教版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 171.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 10:57:07 | ||
图片预览

文档简介
5.2.2 平行线的判定
【练基础】
必备知识1 同位角相等,两直线平行
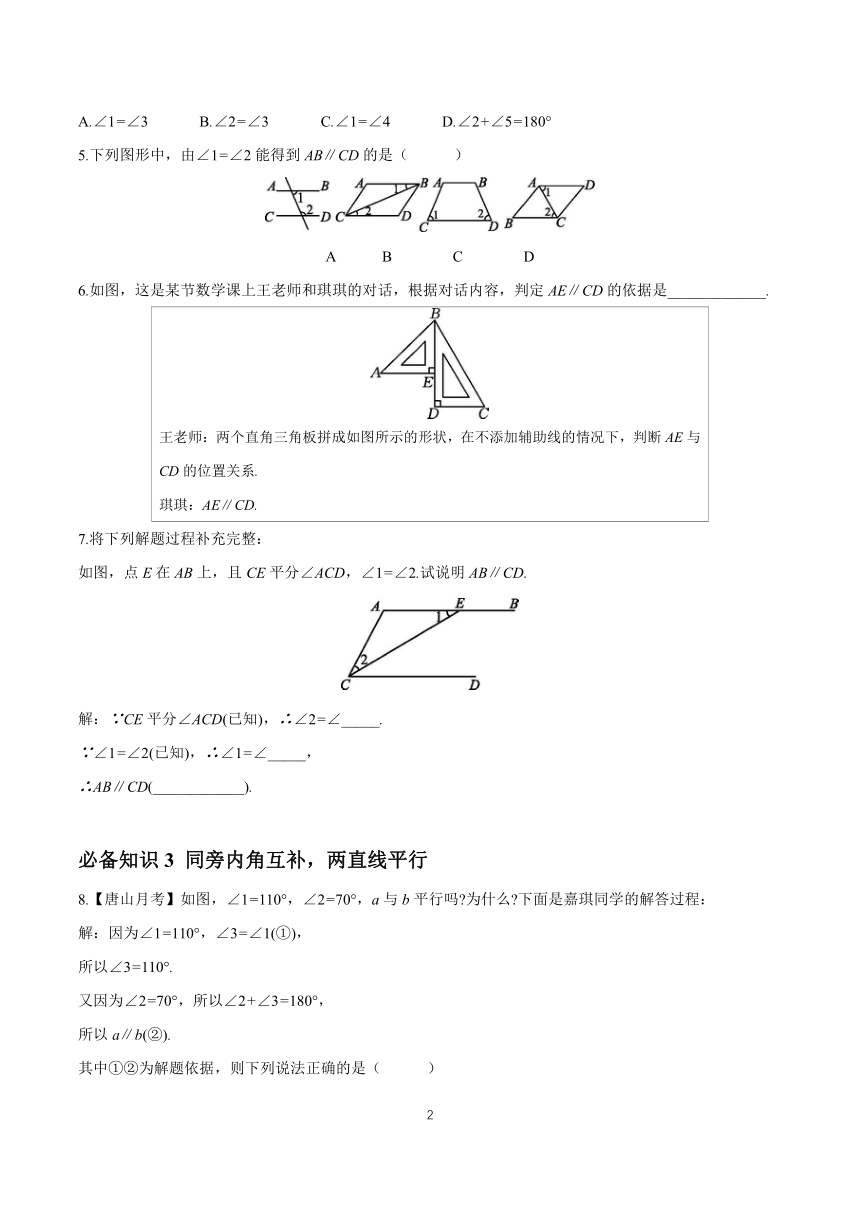
1.【教材P16习题5.2T7变式】如图,∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD C.AD∥EF D.EF∥BC
2.如图,将木条a,b与木条c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,则木条a旋转的度数至少是( )
A.10° B.20° C.50° D.70°
3.如图,已知A,B是直线GH上两点,AC⊥AE,BD⊥BF,∠1=∠2,试说明AE∥BF.
必备知识2 内错角相等,两直线平行
4.如图,直线a,b被直线c所截,下列条件能判定a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.∠2+∠5=180°
5.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A B C D
6.如图,这是某节数学课上王老师和琪琪的对话,根据对话内容,判定AE∥CD的依据是_____________.
王老师:两个直角三角板拼成如图所示的形状,在不添加辅助线的情况下,判断AE与CD的位置关系. 琪琪:AE∥CD.
7.将下列解题过程补充完整:
如图,点E在AB上,且CE平分∠ACD,∠1=∠2.试说明AB∥CD.
解:∵CE平分∠ACD(已知),∴∠2=∠_____.
∵∠1=∠2(已知),∴∠1=∠_____,
∴AB∥CD(____________).
必备知识3 同旁内角互补,两直线平行
8.【唐山月考】如图,∠1=110°,∠2=70°,a与b平行吗 为什么 下面是嘉琪同学的解答过程:
解:因为∠1=110°,∠3=∠1(①),
所以∠3=110°.
又因为∠2=70°,所以∠2+∠3=180°,
所以a∥b(②).
其中①②为解题依据,则下列说法正确的是( )
A.①代表内错角相等
B.②代表同位角相等,两直线平行
C.①代表对顶角相等
D.②代表同旁内角相等,两直线平行
9.如图,∠1=∠2,∠3+∠4=180°,试说明AB∥EF.
【练能力】
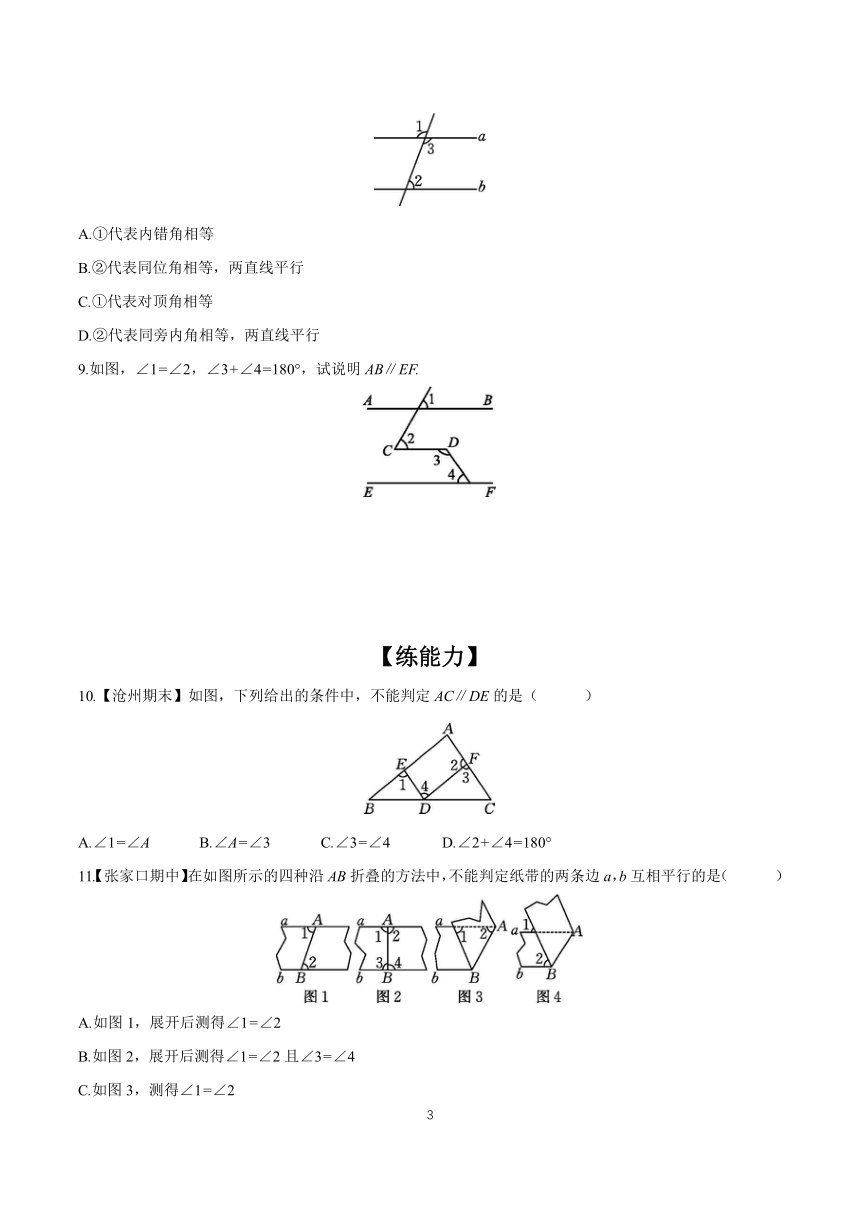
10.【沧州期末】如图,下列给出的条件中,不能判定AC∥DE的是( )
A.∠1=∠A B.∠A=∠3 C.∠3=∠4 D.∠2+∠4=180°
11.【张家口期中】在如图所示的四种沿AB折叠的方法中,不能判定纸带的两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,测得∠1=∠2
12.如图,填空:
(1)若∠A=∠3,则____∥____,理由是_____________.
(2)若∠2=∠E,则____∥____,理由是_____________.
(3)若∠A+∠ABE=180°,则____∥____,理由是________________.
(4)若∠2=∠___,则AD∥BE,理由是_____________.
(5)若∠DBC+∠___=180°,则DB∥EC,理由是____________________
【练素养】
13.如图,将一副三角板中的两个直角顶点C叠放在一起,其中∠A=30°,∠B=60°,∠D=∠E=45°.
【观察猜想】(1)∠BCD与∠ACE的数量关系是____;∠BCE与∠ACD的数量关系是____.
【类比探究】(2)若保持三角板ABC不动,绕直角顶点C顺时针转动三角板DCE,试探究当∠ACD等于多少度时,CE∥AB,画出图形并简要说明理由.
【拓展应用】(3)若∠BCE=3∠ACD,求∠ACD的度数,并直接写出此时DE与AC的位置关系.
参考答案
【练基础】
1.C 2.B
3.【解析】∵AC⊥AE,BD⊥BF,
∴∠CAE=∠DBF=90°.
又∵∠1=∠2,∴∠CAE+∠1=∠DBF+∠2,
即∠EAG=∠FBG,∴AE∥BF.
4.A 5.B
6.内错角相等,两直线平行
7.ECD ECD 内错角相等两直线平行
8.C
9.【解析】∵∠1=∠2,
∴AB∥CD.
∵∠3+∠4=180°,
∴CD∥EF,∴AB∥EF.
【练能力】
10.B 11.C
12.(1)AD BE 同位角相等,两直线平行
(2)BD CE 内错角相等,两直线平行
(3)AD BE 同旁内角互补,两直线平行
(4)D 内错角相等,两直线平行
(5)C 同旁内角互补,两直线平行
【练素养】
13.【解析】(1)∠BCD=∠ACE;∠BCE+∠ACD=180°.
提示:∵∠BCD+∠ACD=90°,∠ACE+∠ACD=90°,
∴∠BCD=∠ACE.
∵∠BCE=∠ACB+∠ACE=90°+∠ACE,
∴∠BCE+∠ACD=90°+∠ACE+∠ACD=90°+90°=180°,
∴∠BCE+∠ACD=180°.
(2)分两种情况:
①如图1,当CE∥AB时,∠ACE=∠A=30°,
∴∠ACD=∠DCE-∠ACE=90°-30°=60°.
②如图2,当CE∥AB时,∠BCE=∠B=60°,
∴∠ACD=360°-∠ACB-∠BCE-∠DCE=360°-90°-60°-90°=120°.
综上所述,当∠ACD等于60°或120°时,CE∥AB.
(3)设∠ACD=α,则∠BCE=3α.
由(1)可知,∠BCE+∠ACD=180°,
∴3α+α=180°,∴α=45°,即∠ACD=45°,
此时DE⊥AC或DE∥AC.
2
【练基础】
必备知识1 同位角相等,两直线平行
1.【教材P16习题5.2T7变式】如图,∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD C.AD∥EF D.EF∥BC
2.如图,将木条a,b与木条c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,则木条a旋转的度数至少是( )
A.10° B.20° C.50° D.70°
3.如图,已知A,B是直线GH上两点,AC⊥AE,BD⊥BF,∠1=∠2,试说明AE∥BF.
必备知识2 内错角相等,两直线平行
4.如图,直线a,b被直线c所截,下列条件能判定a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.∠2+∠5=180°
5.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A B C D
6.如图,这是某节数学课上王老师和琪琪的对话,根据对话内容,判定AE∥CD的依据是_____________.
王老师:两个直角三角板拼成如图所示的形状,在不添加辅助线的情况下,判断AE与CD的位置关系. 琪琪:AE∥CD.
7.将下列解题过程补充完整:
如图,点E在AB上,且CE平分∠ACD,∠1=∠2.试说明AB∥CD.
解:∵CE平分∠ACD(已知),∴∠2=∠_____.
∵∠1=∠2(已知),∴∠1=∠_____,
∴AB∥CD(____________).
必备知识3 同旁内角互补,两直线平行
8.【唐山月考】如图,∠1=110°,∠2=70°,a与b平行吗 为什么 下面是嘉琪同学的解答过程:
解:因为∠1=110°,∠3=∠1(①),
所以∠3=110°.
又因为∠2=70°,所以∠2+∠3=180°,
所以a∥b(②).
其中①②为解题依据,则下列说法正确的是( )
A.①代表内错角相等
B.②代表同位角相等,两直线平行
C.①代表对顶角相等
D.②代表同旁内角相等,两直线平行
9.如图,∠1=∠2,∠3+∠4=180°,试说明AB∥EF.
【练能力】
10.【沧州期末】如图,下列给出的条件中,不能判定AC∥DE的是( )
A.∠1=∠A B.∠A=∠3 C.∠3=∠4 D.∠2+∠4=180°
11.【张家口期中】在如图所示的四种沿AB折叠的方法中,不能判定纸带的两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,测得∠1=∠2
12.如图,填空:
(1)若∠A=∠3,则____∥____,理由是_____________.
(2)若∠2=∠E,则____∥____,理由是_____________.
(3)若∠A+∠ABE=180°,则____∥____,理由是________________.
(4)若∠2=∠___,则AD∥BE,理由是_____________.
(5)若∠DBC+∠___=180°,则DB∥EC,理由是____________________
【练素养】
13.如图,将一副三角板中的两个直角顶点C叠放在一起,其中∠A=30°,∠B=60°,∠D=∠E=45°.
【观察猜想】(1)∠BCD与∠ACE的数量关系是____;∠BCE与∠ACD的数量关系是____.
【类比探究】(2)若保持三角板ABC不动,绕直角顶点C顺时针转动三角板DCE,试探究当∠ACD等于多少度时,CE∥AB,画出图形并简要说明理由.
【拓展应用】(3)若∠BCE=3∠ACD,求∠ACD的度数,并直接写出此时DE与AC的位置关系.
参考答案
【练基础】
1.C 2.B
3.【解析】∵AC⊥AE,BD⊥BF,
∴∠CAE=∠DBF=90°.
又∵∠1=∠2,∴∠CAE+∠1=∠DBF+∠2,
即∠EAG=∠FBG,∴AE∥BF.
4.A 5.B
6.内错角相等,两直线平行
7.ECD ECD 内错角相等两直线平行
8.C
9.【解析】∵∠1=∠2,
∴AB∥CD.
∵∠3+∠4=180°,
∴CD∥EF,∴AB∥EF.
【练能力】
10.B 11.C
12.(1)AD BE 同位角相等,两直线平行
(2)BD CE 内错角相等,两直线平行
(3)AD BE 同旁内角互补,两直线平行
(4)D 内错角相等,两直线平行
(5)C 同旁内角互补,两直线平行
【练素养】
13.【解析】(1)∠BCD=∠ACE;∠BCE+∠ACD=180°.
提示:∵∠BCD+∠ACD=90°,∠ACE+∠ACD=90°,
∴∠BCD=∠ACE.
∵∠BCE=∠ACB+∠ACE=90°+∠ACE,
∴∠BCE+∠ACD=90°+∠ACE+∠ACD=90°+90°=180°,
∴∠BCE+∠ACD=180°.
(2)分两种情况:
①如图1,当CE∥AB时,∠ACE=∠A=30°,
∴∠ACD=∠DCE-∠ACE=90°-30°=60°.
②如图2,当CE∥AB时,∠BCE=∠B=60°,
∴∠ACD=360°-∠ACB-∠BCE-∠DCE=360°-90°-60°-90°=120°.
综上所述,当∠ACD等于60°或120°时,CE∥AB.
(3)设∠ACD=α,则∠BCE=3α.
由(1)可知,∠BCE+∠ACD=180°,
∴3α+α=180°,∴α=45°,即∠ACD=45°,
此时DE⊥AC或DE∥AC.
2
