5.3.1 平行线的性质 分层作业(含答案) 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 5.3.1 平行线的性质 分层作业(含答案) 2023-2024学年初中数学人教版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 152.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 00:00:00 | ||
图片预览

文档简介
5.3.1 平行线的性质
【练基础】
1.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A B C D
2.如图,∠ABE=80°,BF是∠ABE的平分线,且BF∥CD,求∠C的度数.
3.如图,AB∥CD,CE平分∠BCD,∠B=36°,则∠DCE的度数为( )
A.18° B.36° C.45° D.54°
4.如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为( )
A.20° B.35° C.55° D.70°
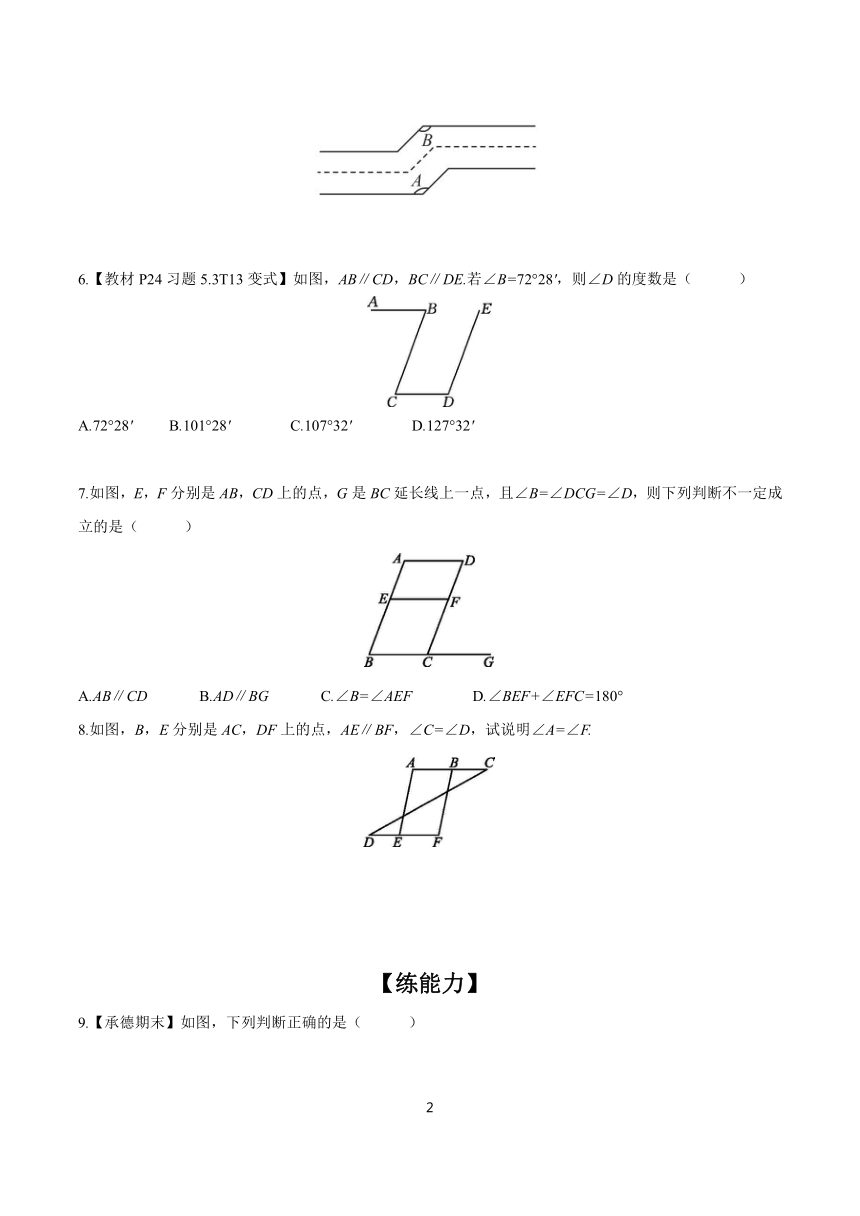
5.如图,一条公路两次转弯后和原来的方向相同,第一次的拐角∠A是130°,则第二次的拐角∠B也是130°的依据是_________.
6.【教材P24习题5.3T13变式】如图,AB∥CD,BC∥DE.若∠B=72°28',则∠D的度数是( )
A.72°28' B.101°28' C.107°32' D.127°32'
7.如图,E,F分别是AB,CD上的点,G是BC延长线上一点,且∠B=∠DCG=∠D,则下列判断不一定成立的是( )
A.AB∥CD B.AD∥BG C.∠B=∠AEF D.∠BEF+∠EFC=180°
8.如图,B,E分别是AC,DF上的点,AE∥BF,∠C=∠D,试说明∠A=∠F.
【练能力】
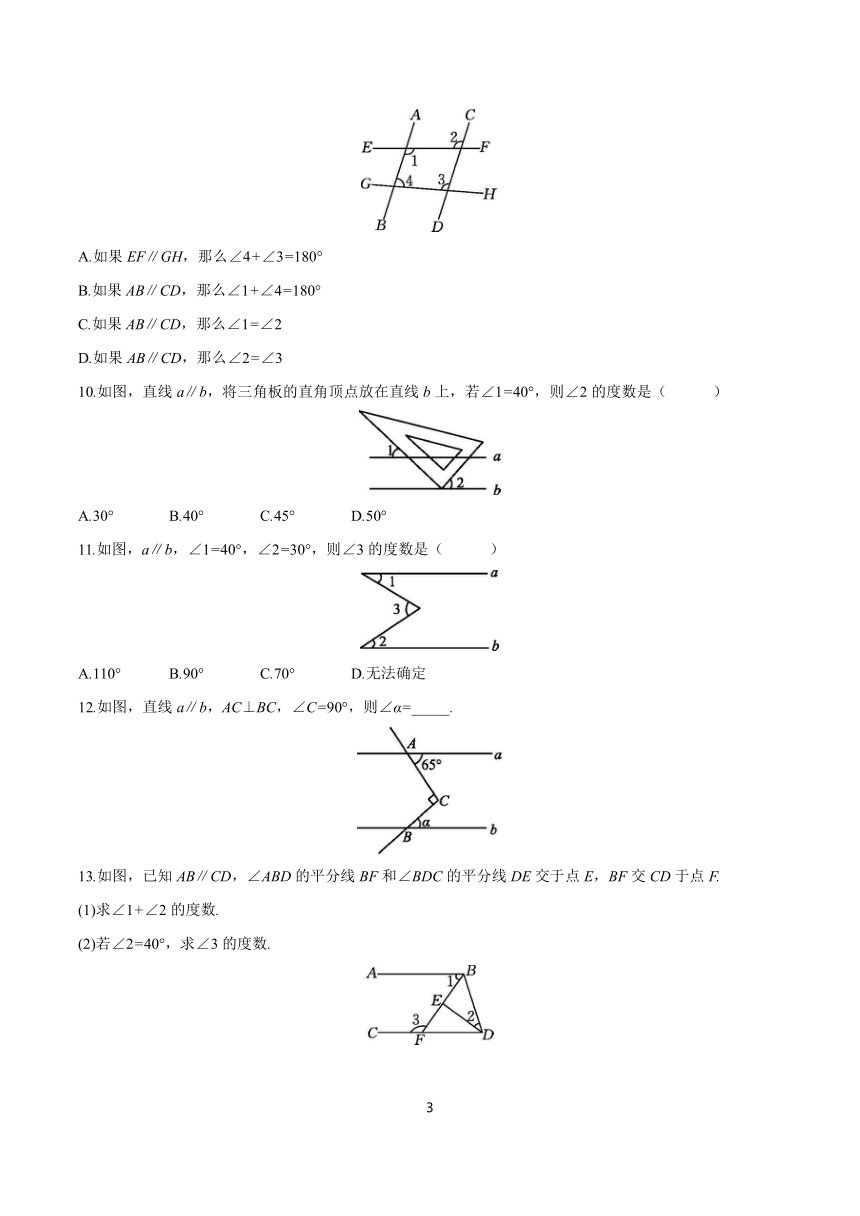
9.【承德期末】如图,下列判断正确的是( )
A.如果EF∥GH,那么∠4+∠3=180°
B.如果AB∥CD,那么∠1+∠4=180°
C.如果AB∥CD,那么∠1=∠2
D.如果AB∥CD,那么∠2=∠3
10.如图,直线a∥b,将三角板的直角顶点放在直线b上,若∠1=40°,则∠2的度数是( )
A.30° B.40° C.45° D.50°
11.如图,a∥b,∠1=40°,∠2=30°,则∠3的度数是( )
A.110° B.90° C.70° D.无法确定
12.如图,直线a∥b,AC⊥BC,∠C=90°,则∠α=_____.
13.如图,已知AB∥CD,∠ABD的平分线BF和∠BDC的平分线DE交于点E,BF交CD于点F.
(1)求∠1+∠2的度数.
(2)若∠2=40°,求∠3的度数.
【练素养】
14.课上数学老师呈现一个问题:
如图,AB∥CD,EF⊥AB于点O,FG交CD于点P,当∠1=30°时,求∠EFG的度数.
甲、乙、丙三位同学用不同的方法添加辅助线解决问题,如图所示:
甲同学辅助线的作法和分析思路如下.
辅助线:__________ 分析思路: (1)欲求∠EFG的度数,由图可知只需求出∠2和∠3的度数; (2)由MN∥CD可知,∠2=∠1,已知∠1的度数,可得∠2的度数; (3)由AB∥CD,MN∥CD推出AB∥MN,由此可推出∠3=∠4; (4)已知EF⊥AB,可得∠4=90°,所以可得∠3的度数; (5)从而可求出∠EFG的度数.
请你选择乙同学或丙同学所画的图形,描述辅助线的作法,并写出相应的分析思路.
参考答案
【练基础】
1.B
2.【解析】∵BF是∠ABE的平分线,
∴∠ABF=∠ABE.
∵∠ABE=80°,∴∠ABF=40°.
∵BF∥CD,∴∠C=∠ABF,
∴∠C=40°.
3.A 4.B
5.两直线平行,内错角相等
6.C 7.C
8.【解析】∵AE∥BF,∴∠AED=∠F.
∵∠C=∠D,∴AC∥DF,
∴∠AED=∠A,∴∠A=∠F.
【练能力】
9.C 10.D 11.C 12.25°
13.【解析】(1)因为BF,DE分别平分∠ABD和∠BDC,
所以∠ABD=2∠1,∠BDC=2∠2.
因为AB∥CD,所以∠ABD+∠BDC=180°,
即2∠1+2∠2=180°,所以∠1+∠2=90°.
(2)因为∠2=40°,
由(1)知∠1+∠2=90°,
所以∠1=90°-∠2=50°.
因为AB∥CD,所以∠1+∠3=180°,
所以∠3=180°-∠1=130°.
【练素养】
14.【解析】甲同学辅助线:过点F作MN∥CD.
选择乙同学所画的图形.
辅助线:过点P作PH∥EF,交AB于点H.
分析思路:
(1)欲求∠EFG的度数,由PH∥EF可知,∠EFG=∠HPG,因此,只需求出∠HPG的度数;
(2)欲求∠HPG的度数,由题图可知只需求出∠1和∠2的度数;
(3)已知∠1的度数,所以只需求出∠2的度数;
(4)已知EF⊥AB,可得∠4=90°;
(5)由PH∥EF可推出∠3=∠4,由AB∥CD可推出∠2=∠3,由此可推出∠2=∠4,所以可得∠2的度数;
(6)从而可求出∠EFG的度数.
选择丙同学所画的图形.
辅助线:过点O作OQ∥FG交CD于点K.
分析思路:
(1)欲求∠EFG的度数,由OQ∥FG可知,∠EFG=∠EOQ,因此,只需求出∠EOQ的度数;
(2)欲求∠EOQ的度数,由题图可知只需求出∠2和∠3的度数;
(3)已知EF⊥AB,可得∠3=90°;
(4)由AB∥CD可推出∠2=∠4,由OQ∥FG可推出∠4=∠1,由此可推出∠2=∠1,所以可得∠2的度数;
(5)从而可求出∠EFG的度数.
(选择任意一种即可)
2
【练基础】
1.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A B C D
2.如图,∠ABE=80°,BF是∠ABE的平分线,且BF∥CD,求∠C的度数.
3.如图,AB∥CD,CE平分∠BCD,∠B=36°,则∠DCE的度数为( )
A.18° B.36° C.45° D.54°
4.如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为( )
A.20° B.35° C.55° D.70°
5.如图,一条公路两次转弯后和原来的方向相同,第一次的拐角∠A是130°,则第二次的拐角∠B也是130°的依据是_________.
6.【教材P24习题5.3T13变式】如图,AB∥CD,BC∥DE.若∠B=72°28',则∠D的度数是( )
A.72°28' B.101°28' C.107°32' D.127°32'
7.如图,E,F分别是AB,CD上的点,G是BC延长线上一点,且∠B=∠DCG=∠D,则下列判断不一定成立的是( )
A.AB∥CD B.AD∥BG C.∠B=∠AEF D.∠BEF+∠EFC=180°
8.如图,B,E分别是AC,DF上的点,AE∥BF,∠C=∠D,试说明∠A=∠F.
【练能力】
9.【承德期末】如图,下列判断正确的是( )
A.如果EF∥GH,那么∠4+∠3=180°
B.如果AB∥CD,那么∠1+∠4=180°
C.如果AB∥CD,那么∠1=∠2
D.如果AB∥CD,那么∠2=∠3
10.如图,直线a∥b,将三角板的直角顶点放在直线b上,若∠1=40°,则∠2的度数是( )
A.30° B.40° C.45° D.50°
11.如图,a∥b,∠1=40°,∠2=30°,则∠3的度数是( )
A.110° B.90° C.70° D.无法确定
12.如图,直线a∥b,AC⊥BC,∠C=90°,则∠α=_____.
13.如图,已知AB∥CD,∠ABD的平分线BF和∠BDC的平分线DE交于点E,BF交CD于点F.
(1)求∠1+∠2的度数.
(2)若∠2=40°,求∠3的度数.
【练素养】
14.课上数学老师呈现一个问题:
如图,AB∥CD,EF⊥AB于点O,FG交CD于点P,当∠1=30°时,求∠EFG的度数.
甲、乙、丙三位同学用不同的方法添加辅助线解决问题,如图所示:
甲同学辅助线的作法和分析思路如下.
辅助线:__________ 分析思路: (1)欲求∠EFG的度数,由图可知只需求出∠2和∠3的度数; (2)由MN∥CD可知,∠2=∠1,已知∠1的度数,可得∠2的度数; (3)由AB∥CD,MN∥CD推出AB∥MN,由此可推出∠3=∠4; (4)已知EF⊥AB,可得∠4=90°,所以可得∠3的度数; (5)从而可求出∠EFG的度数.
请你选择乙同学或丙同学所画的图形,描述辅助线的作法,并写出相应的分析思路.
参考答案
【练基础】
1.B
2.【解析】∵BF是∠ABE的平分线,
∴∠ABF=∠ABE.
∵∠ABE=80°,∴∠ABF=40°.
∵BF∥CD,∴∠C=∠ABF,
∴∠C=40°.
3.A 4.B
5.两直线平行,内错角相等
6.C 7.C
8.【解析】∵AE∥BF,∴∠AED=∠F.
∵∠C=∠D,∴AC∥DF,
∴∠AED=∠A,∴∠A=∠F.
【练能力】
9.C 10.D 11.C 12.25°
13.【解析】(1)因为BF,DE分别平分∠ABD和∠BDC,
所以∠ABD=2∠1,∠BDC=2∠2.
因为AB∥CD,所以∠ABD+∠BDC=180°,
即2∠1+2∠2=180°,所以∠1+∠2=90°.
(2)因为∠2=40°,
由(1)知∠1+∠2=90°,
所以∠1=90°-∠2=50°.
因为AB∥CD,所以∠1+∠3=180°,
所以∠3=180°-∠1=130°.
【练素养】
14.【解析】甲同学辅助线:过点F作MN∥CD.
选择乙同学所画的图形.
辅助线:过点P作PH∥EF,交AB于点H.
分析思路:
(1)欲求∠EFG的度数,由PH∥EF可知,∠EFG=∠HPG,因此,只需求出∠HPG的度数;
(2)欲求∠HPG的度数,由题图可知只需求出∠1和∠2的度数;
(3)已知∠1的度数,所以只需求出∠2的度数;
(4)已知EF⊥AB,可得∠4=90°;
(5)由PH∥EF可推出∠3=∠4,由AB∥CD可推出∠2=∠3,由此可推出∠2=∠4,所以可得∠2的度数;
(6)从而可求出∠EFG的度数.
选择丙同学所画的图形.
辅助线:过点O作OQ∥FG交CD于点K.
分析思路:
(1)欲求∠EFG的度数,由OQ∥FG可知,∠EFG=∠EOQ,因此,只需求出∠EOQ的度数;
(2)欲求∠EOQ的度数,由题图可知只需求出∠2和∠3的度数;
(3)已知EF⊥AB,可得∠3=90°;
(4)由AB∥CD可推出∠2=∠4,由OQ∥FG可推出∠4=∠1,由此可推出∠2=∠1,所以可得∠2的度数;
(5)从而可求出∠EFG的度数.
(选择任意一种即可)
2
