5.3.2 命题、定理、证明 分层作业(含答案) 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 5.3.2 命题、定理、证明 分层作业(含答案) 2023-2024学年初中数学人教版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 79.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 16:28:12 | ||
图片预览


文档简介
5.3.2 命题、定理、证明
【练基础】
1.【唐山期中】下列语句中,是命题的是( )
A.美丽的天空 B.相等的角是对顶角 C.作线段AB=CD D.你喜欢运动吗
2.下列语句中不是命题的是( )
A.对顶角不相等 B.过A,B两点作直线 C.两点之间线段最短 D.内错角相等
3.命题“等角的补角相等”中,“等角的补角”是命题的( )
A.条件部分 B.是条件,也是结论 C.结论部分 D.不是条件,也不是结论
4.【沧州期中】证明命题“若(a-1)2>1,则a>2”是假命题,下面所举反例正确的是( )
A.a=2 B.a=1 C.a=0 D.a=-1
5.【唐山月考】把命题“同角的补角相等”改写成“如果……那么……”的形式:____________________.
6.判断下列命题是真命题还是假命题,如果是假命题,请举一反例.
(1)两个锐角的和是锐角.
(2)如果ab>0,那么a+b>0.
(3)如果一个有理数既不是正数,也不是负数,那么它一定是0.
7.下列说法不正确的是( )
A.证实命题正确与否的推理过程叫做证明
B.定理是命题,而且是真命题
C.“对顶角相等”是命题,但不是定理
D.要证明一个命题是假命题只要举出一个反例即可
8.对于命题“|a|=a(a为实数)”,能说明它是假命题的反例是a=___________(请写出一个符合条件的a的值).
9.在下面的括号内,填上推理的依据.
如图,C,P,D三点在同一条直线上,∠BAP与∠APD互补,∠1=∠2.求证:∠E=∠F.
证明:∵∠BAP+∠APD=180°(____),
∴AB∥CD(____________),
∴∠BAP=∠APC(_________________).
又∵∠1=∠2(____),
∴∠BAP-∠2=∠APC-∠1,
即∠EAP=∠APF(_______),
∴AE∥PF(_____________),
∴∠E=∠F(___________).
【练能力】
10.【邯郸期末】命题“垂直于同一条直线的两条直线互相平行”的题设是( )
A.垂直
B.两条直线
C.同一条直线
D.两条直线垂直于同一条直线
11.用一组a,b,c的整数值说明命题“若a>b>c,则ab>c”是假命题,则这组值可以是a=___,b=____,c=____.
12.将下列命题改写成“如果…那么…”的形式,并判断命题的真假,若是假命题请举反例.
(1)相等的角是对顶角.
(2)直角三角形的两个锐角互余.
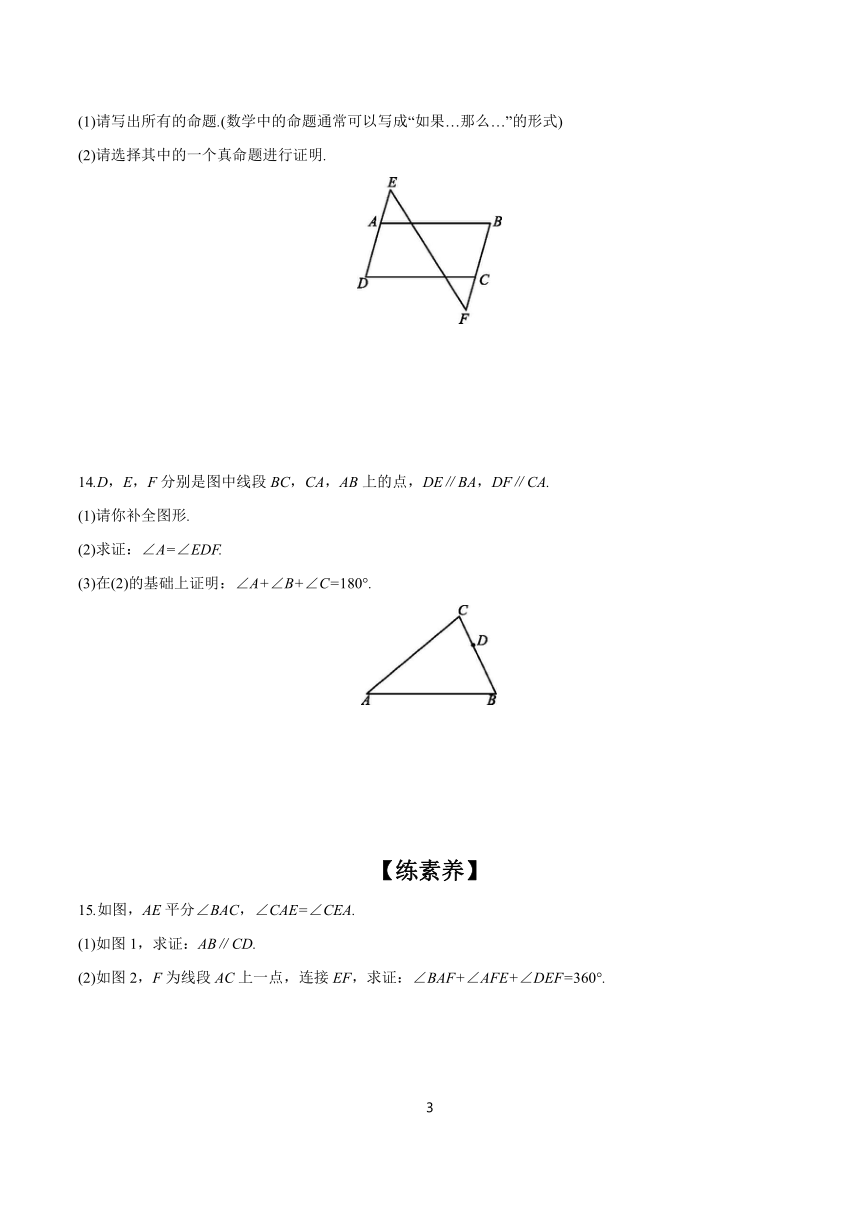
13.如图,现有以下三个条件:①AB∥CD;②∠B=∠D;③∠E=∠F.请以其中两个条件为条件,第三个条件为结论构造新的命题.
(1)请写出所有的命题.(数学中的命题通常可以写成“如果…那么…”的形式)
(2)请选择其中的一个真命题进行证明.
14.D,E,F分别是图中线段BC,CA,AB上的点,DE∥BA,DF∥CA.
(1)请你补全图形.
(2)求证:∠A=∠EDF.
(3)在(2)的基础上证明:∠A+∠B+∠C=180°.
【练素养】
15.如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD.
(2)如图2,F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°.
参考答案
【练基础】
1.B 2.B 3.A 4.D
5.如果两个角为同一个角的补角,那么这两个角相等
6.【解析】(1)假命题.反例:40°与60°.
(2)假命题.反例:a=-1,b=-2.
(3)真命题.
7.C
8.-1(答案不唯一)
9.已知 同旁内角互补,两直线平行 两直线平行,内错角相等 已知 等式的性质 内错角相等,两直线平行 两直线平行,内错角相等
【练能力】
10.D
11.3 -2 -5
【解析】(答案不唯一)在满足a>b>c的条件下,使ab≤c即可.
12.【解析】(1)如果两个角相等,那么这两个角是对顶角;假命题.
反例:角平分线形成的两个角相等,但不是对顶角.(表述不唯一)
(2)如果一个三角形是直角三角形,那么它的两锐角互余;真命题.
13.【解析】(1)第一种:如果AB∥CD,∠B=∠D,那么∠E=∠F.
第二种:如果AB∥CD,∠E=∠F,那么∠B=∠D.
第三种:如果∠B=∠D,∠E=∠F,那么AB∥CD.
(2)证明第一种;
∵AB∥CD,∴∠B=∠DCF.
∵∠B=∠D,∴∠D=∠DCF,
∴DE∥BF,∴∠E=∠F.
14.【解析】(1)如图所示.
(2)证明:∵DE∥BA,
∴∠EDF=∠BFD.
∵DF∥CA,
∴∠A=∠BFD,
∴∠A=∠EDF.
(3)证明:∵DE∥BA,
∴∠B=∠CDE(两直线平行,同位角相等).
∵DF∥CA,
∴∠C=∠BDF(两直线平行,同位角相等).
由(2)知∠A=∠EDF.
∵∠EDF+∠CDE+∠BDF=180°(平角的定义),
∴∠A+∠B+∠C=180°(等量代换).
【练素养】
15.【解析】(1)∵AE平分∠BAC,
∴∠BAE=∠CAE.
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD.
(2)如图,过点F作FM∥AB.
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFM=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°.
2
【练基础】
1.【唐山期中】下列语句中,是命题的是( )
A.美丽的天空 B.相等的角是对顶角 C.作线段AB=CD D.你喜欢运动吗
2.下列语句中不是命题的是( )
A.对顶角不相等 B.过A,B两点作直线 C.两点之间线段最短 D.内错角相等
3.命题“等角的补角相等”中,“等角的补角”是命题的( )
A.条件部分 B.是条件,也是结论 C.结论部分 D.不是条件,也不是结论
4.【沧州期中】证明命题“若(a-1)2>1,则a>2”是假命题,下面所举反例正确的是( )
A.a=2 B.a=1 C.a=0 D.a=-1
5.【唐山月考】把命题“同角的补角相等”改写成“如果……那么……”的形式:____________________.
6.判断下列命题是真命题还是假命题,如果是假命题,请举一反例.
(1)两个锐角的和是锐角.
(2)如果ab>0,那么a+b>0.
(3)如果一个有理数既不是正数,也不是负数,那么它一定是0.
7.下列说法不正确的是( )
A.证实命题正确与否的推理过程叫做证明
B.定理是命题,而且是真命题
C.“对顶角相等”是命题,但不是定理
D.要证明一个命题是假命题只要举出一个反例即可
8.对于命题“|a|=a(a为实数)”,能说明它是假命题的反例是a=___________(请写出一个符合条件的a的值).
9.在下面的括号内,填上推理的依据.
如图,C,P,D三点在同一条直线上,∠BAP与∠APD互补,∠1=∠2.求证:∠E=∠F.
证明:∵∠BAP+∠APD=180°(____),
∴AB∥CD(____________),
∴∠BAP=∠APC(_________________).
又∵∠1=∠2(____),
∴∠BAP-∠2=∠APC-∠1,
即∠EAP=∠APF(_______),
∴AE∥PF(_____________),
∴∠E=∠F(___________).
【练能力】
10.【邯郸期末】命题“垂直于同一条直线的两条直线互相平行”的题设是( )
A.垂直
B.两条直线
C.同一条直线
D.两条直线垂直于同一条直线
11.用一组a,b,c的整数值说明命题“若a>b>c,则ab>c”是假命题,则这组值可以是a=___,b=____,c=____.
12.将下列命题改写成“如果…那么…”的形式,并判断命题的真假,若是假命题请举反例.
(1)相等的角是对顶角.
(2)直角三角形的两个锐角互余.
13.如图,现有以下三个条件:①AB∥CD;②∠B=∠D;③∠E=∠F.请以其中两个条件为条件,第三个条件为结论构造新的命题.
(1)请写出所有的命题.(数学中的命题通常可以写成“如果…那么…”的形式)
(2)请选择其中的一个真命题进行证明.
14.D,E,F分别是图中线段BC,CA,AB上的点,DE∥BA,DF∥CA.
(1)请你补全图形.
(2)求证:∠A=∠EDF.
(3)在(2)的基础上证明:∠A+∠B+∠C=180°.
【练素养】
15.如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD.
(2)如图2,F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°.
参考答案
【练基础】
1.B 2.B 3.A 4.D
5.如果两个角为同一个角的补角,那么这两个角相等
6.【解析】(1)假命题.反例:40°与60°.
(2)假命题.反例:a=-1,b=-2.
(3)真命题.
7.C
8.-1(答案不唯一)
9.已知 同旁内角互补,两直线平行 两直线平行,内错角相等 已知 等式的性质 内错角相等,两直线平行 两直线平行,内错角相等
【练能力】
10.D
11.3 -2 -5
【解析】(答案不唯一)在满足a>b>c的条件下,使ab≤c即可.
12.【解析】(1)如果两个角相等,那么这两个角是对顶角;假命题.
反例:角平分线形成的两个角相等,但不是对顶角.(表述不唯一)
(2)如果一个三角形是直角三角形,那么它的两锐角互余;真命题.
13.【解析】(1)第一种:如果AB∥CD,∠B=∠D,那么∠E=∠F.
第二种:如果AB∥CD,∠E=∠F,那么∠B=∠D.
第三种:如果∠B=∠D,∠E=∠F,那么AB∥CD.
(2)证明第一种;
∵AB∥CD,∴∠B=∠DCF.
∵∠B=∠D,∴∠D=∠DCF,
∴DE∥BF,∴∠E=∠F.
14.【解析】(1)如图所示.
(2)证明:∵DE∥BA,
∴∠EDF=∠BFD.
∵DF∥CA,
∴∠A=∠BFD,
∴∠A=∠EDF.
(3)证明:∵DE∥BA,
∴∠B=∠CDE(两直线平行,同位角相等).
∵DF∥CA,
∴∠C=∠BDF(两直线平行,同位角相等).
由(2)知∠A=∠EDF.
∵∠EDF+∠CDE+∠BDF=180°(平角的定义),
∴∠A+∠B+∠C=180°(等量代换).
【练素养】
15.【解析】(1)∵AE平分∠BAC,
∴∠BAE=∠CAE.
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD.
(2)如图,过点F作FM∥AB.
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFM=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°.
2
