7.1.2 平面直角坐标系 分层作业 (含答案)2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 7.1.2 平面直角坐标系 分层作业 (含答案)2023-2024学年初中数学人教版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 124.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 17:40:09 | ||
图片预览


文档简介
7.1.2 平面直角坐标系
【练基础】
必备知识1 平面直角坐标系的概念
1.平面内两条互相____并且原点____的____,组成平面直角坐标系.其中,水平的数轴称为____或____,习惯上取______为正方向;竖直的数轴称为____或____,取______为正方向;两坐标轴的交点叫做平面直角坐标系的____.直角坐标系所在的____叫做坐标平面.
必备知识2 点的坐标的定义
2.在平面直角坐标系内,任何一点的坐标是( )
A.一对整数 B.一对实数 C.一对有序实数 D.一对有序有理数
3.如果点A既在x轴的上方,又在y轴的左边,且距离x轴,y轴分别为5个和4个单位长度,那么点A的坐标为( )
A.(5,-4) B.(4,-5) C.(-5,4) D.(-4,5)
4.已知点M到x轴的距离为1,到y轴的距离为2,则点M的坐标为( )
A.(1,2) B.(-1,-2) C.(1,-2) D.(2,1)或(2,-1)或(-2,1)或(-2,-1)
5.【教材P68练习T1变式】如图,点A,B,C,D的坐标分别为____________________.
必备知识3 平面内点的坐标的特征
6.下列各点中,位于平面直角坐标系第四象限的点是( )
A.(-2,1) B.(-2,-1) C.(2,-1) D.(0,-1)
7.在平面直角坐标系中,点(-6,a2+6)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.过A(-2,2),B(-2,-3)两点作直线,下列说法中,正确的是( )
A.AB⊥x轴 B.AB⊥y轴 C.AB∥x轴 D.AB过原点
9.若点A(m,-n)在第二象限,则点B(-m,|n|)在第_______象限.
【练能力】
10.【2022石家庄期中】已知点P的横坐标是-3,且到x轴的距离为5,则点P的坐标是( )
A.(-3,-5) B.(-3,5)或(-3,-5) C.(-3,5) D.(5,-3)或(-5,-3)
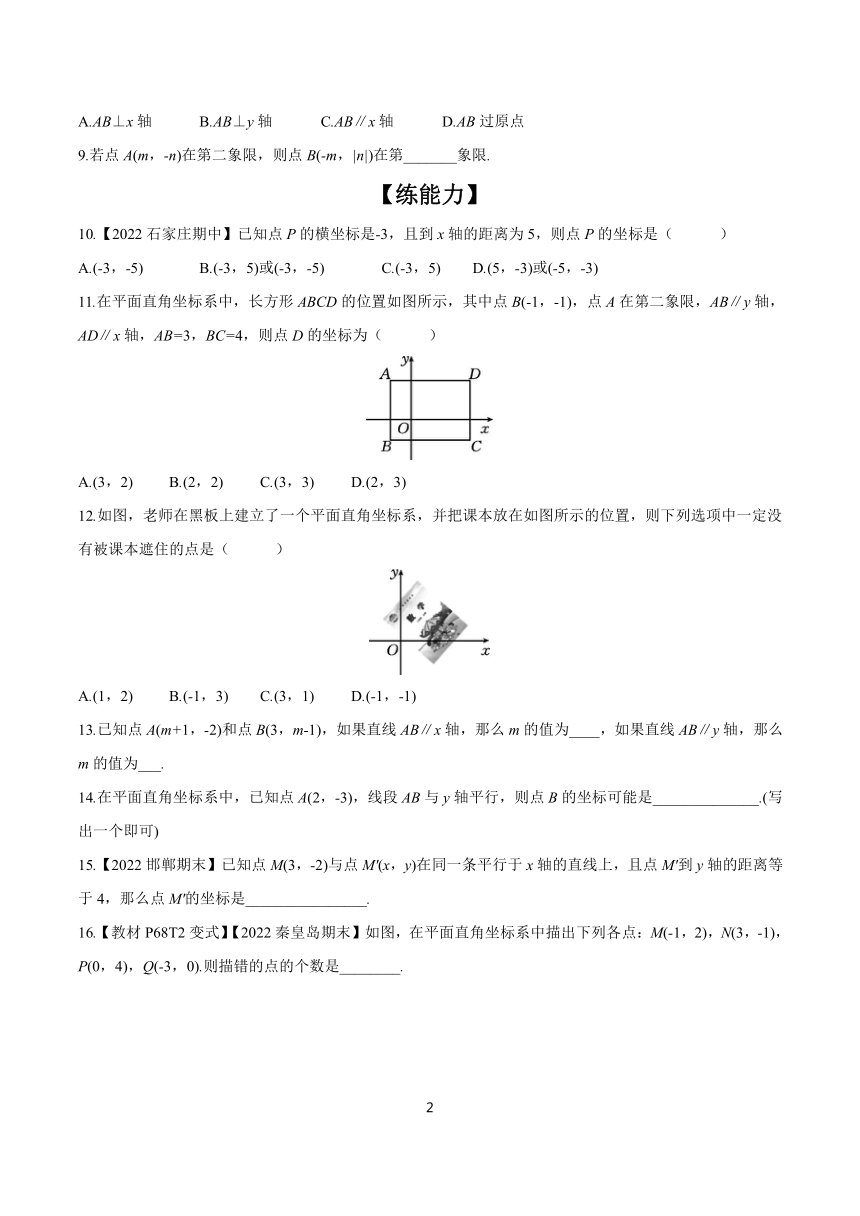
11.在平面直角坐标系中,长方形ABCD的位置如图所示,其中点B(-1,-1),点A在第二象限,AB∥y轴,AD∥x轴,AB=3,BC=4,则点D的坐标为( )
A.(3,2) B.(2,2) C.(3,3) D.(2,3)
12.如图,老师在黑板上建立了一个平面直角坐标系,并把课本放在如图所示的位置,则下列选项中一定没有被课本遮住的点是( )
A.(1,2) B.(-1,3) C.(3,1) D.(-1,-1)
13.已知点A(m+1,-2)和点B(3,m-1),如果直线AB∥x轴,那么m的值为____,如果直线AB∥y轴,那么m的值为___.
14.在平面直角坐标系中,已知点A(2,-3),线段AB与y轴平行,则点B的坐标可能是______________.(写出一个即可)
15.【2022邯郸期末】已知点M(3,-2)与点M'(x,y)在同一条平行于x轴的直线上,且点M'到y轴的距离等于4,那么点M'的坐标是________________.
16.【教材P68T2变式】【2022秦皇岛期末】如图,在平面直角坐标系中描出下列各点:M(-1,2),N(3,-1),P(0,4),Q(-3,0).则描错的点的个数是________.
17.【教材P68练习T2变式】在如图所示的平面直角坐标系中描出下列各点,并将这些点用线段依次连接起来.
(-2,3),(-1,-1),(0,3),(1,-1),(2,3).
18.已知点P(2m+4,m-1),请分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3.
(2)点P在第三象限,且点P到两坐标轴的距离之和为12.
(3)点P在坐标轴上.
【练素养】
19.已知当m,n都是实数,且满足2m=8+n时,称p为“开心点”.例如:A(5,3)为“开心点”.
因为当点A为(5,3)时,m-1=5,=3,得m=6,n=4,
所以2m=2×6=12,8+n=8+4=12,
所以2m=8+n.
所以A(5,3)是“开心点”.
(1)判断点B(4,10)是否为“开心点”,并说明理由.
(2)若点M(a,2a-1)是“开心点”,请判断点M在第几象限,并说明理由.
参考答案
【练基础】
1.垂直 重合 数轴 x轴 横轴 向右方向 y轴 纵轴 向上方向 原点 平面
2.C 3.D 4.D
5.(3,2),(2,3),(-2,3),(-1,-3)
【解析】【归纳总结】确定点的坐标的方法:
(1)确定横坐标:从该点向x轴作垂线,垂足对应的x轴上的数为该点的横坐标.(2)确定纵坐标:从该点向y轴作垂线,垂足对应的y轴上的数为该点的纵坐标.
6.C 7.B 8.A 9.一
【练能力】
10.B 【解析】因为点P到x轴的距离为5,所以点P的纵坐标是5或-5.又因为点P的横坐标是-3,所以点P的坐标是(-3,5)或(-3,-5).
11.A
12.D 【解析】由题图知,只有第三象限没有被课本遮挡,故一定没有被课本遮住的点是(-1,-1).
13.-1 2
【解析】由直线AB∥x轴,可知m-1=-2,所以m=-1.由直线AB∥y轴,可知m+1=3,所以m=2.
14.(2,3)(答案不唯一)
【解析】若线段AB与y轴平行,则点B的横坐标与点A的横坐标相同.
15.(4,-2)或(-4,-2)
16.1
【解析】题图中点P的坐标是(4,0).
17.【解析】如图所示.
【归纳总结】在平面直角坐标系中描点(a,b)的方法:①在x轴上找出表示数a的点,过该点作x轴的垂线;②在y轴上找出表示数b的点,过该点作y轴的垂线,两条垂线的交点就是点(a,b).
18.【解析】(1)由题意得m-1-(2m+4)=3,解得m=-8,
∴2m+4=-12,m-1=-9,
∴点P的坐标为(-12,-9).
(2)由题意得|m-1|+|2m+4|=12,2m+4<0,m-1<0,即-(m-1)-(2m+4)=12,解得m=-5,
∴2m+4=-6,m-1=-6,
∴点P的坐标为(-6,-6).
(3)分情况讨论:①当点P在x轴上时,m-1=0,解得m=1,
∴点P的坐标为(6,0);
②当点P在y轴上时,2m+4=0,解得m=-2,
∴点P的坐标为(0,-3).
综上所述,点P的坐标为(6,0)或(0,-3).
【练素养】
19.【解析】(1)(4,10)不是“开心点”,理由如下:
当B(4,10)时,m-1=4,=10,
解得m=5,n=18,
则2m=10,8+n=8+18=26,
所以2m≠8+n,
所以点B(4,10)不是“开心点”.
(2)点M在第三象限,理由如下:
∵点M(a,2a-1)是“开心点”,
∴m-1=a,=2a-1,
∴m=a+1,n=4a-4.
代入2m=8+n,有2a+2=8+4a-4,
∴a=-1,2a-1=-3,
∴M(-1,-3),
故点M在第三象限.
2
【练基础】
必备知识1 平面直角坐标系的概念
1.平面内两条互相____并且原点____的____,组成平面直角坐标系.其中,水平的数轴称为____或____,习惯上取______为正方向;竖直的数轴称为____或____,取______为正方向;两坐标轴的交点叫做平面直角坐标系的____.直角坐标系所在的____叫做坐标平面.
必备知识2 点的坐标的定义
2.在平面直角坐标系内,任何一点的坐标是( )
A.一对整数 B.一对实数 C.一对有序实数 D.一对有序有理数
3.如果点A既在x轴的上方,又在y轴的左边,且距离x轴,y轴分别为5个和4个单位长度,那么点A的坐标为( )
A.(5,-4) B.(4,-5) C.(-5,4) D.(-4,5)
4.已知点M到x轴的距离为1,到y轴的距离为2,则点M的坐标为( )
A.(1,2) B.(-1,-2) C.(1,-2) D.(2,1)或(2,-1)或(-2,1)或(-2,-1)
5.【教材P68练习T1变式】如图,点A,B,C,D的坐标分别为____________________.
必备知识3 平面内点的坐标的特征
6.下列各点中,位于平面直角坐标系第四象限的点是( )
A.(-2,1) B.(-2,-1) C.(2,-1) D.(0,-1)
7.在平面直角坐标系中,点(-6,a2+6)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.过A(-2,2),B(-2,-3)两点作直线,下列说法中,正确的是( )
A.AB⊥x轴 B.AB⊥y轴 C.AB∥x轴 D.AB过原点
9.若点A(m,-n)在第二象限,则点B(-m,|n|)在第_______象限.
【练能力】
10.【2022石家庄期中】已知点P的横坐标是-3,且到x轴的距离为5,则点P的坐标是( )
A.(-3,-5) B.(-3,5)或(-3,-5) C.(-3,5) D.(5,-3)或(-5,-3)
11.在平面直角坐标系中,长方形ABCD的位置如图所示,其中点B(-1,-1),点A在第二象限,AB∥y轴,AD∥x轴,AB=3,BC=4,则点D的坐标为( )
A.(3,2) B.(2,2) C.(3,3) D.(2,3)
12.如图,老师在黑板上建立了一个平面直角坐标系,并把课本放在如图所示的位置,则下列选项中一定没有被课本遮住的点是( )
A.(1,2) B.(-1,3) C.(3,1) D.(-1,-1)
13.已知点A(m+1,-2)和点B(3,m-1),如果直线AB∥x轴,那么m的值为____,如果直线AB∥y轴,那么m的值为___.
14.在平面直角坐标系中,已知点A(2,-3),线段AB与y轴平行,则点B的坐标可能是______________.(写出一个即可)
15.【2022邯郸期末】已知点M(3,-2)与点M'(x,y)在同一条平行于x轴的直线上,且点M'到y轴的距离等于4,那么点M'的坐标是________________.
16.【教材P68T2变式】【2022秦皇岛期末】如图,在平面直角坐标系中描出下列各点:M(-1,2),N(3,-1),P(0,4),Q(-3,0).则描错的点的个数是________.
17.【教材P68练习T2变式】在如图所示的平面直角坐标系中描出下列各点,并将这些点用线段依次连接起来.
(-2,3),(-1,-1),(0,3),(1,-1),(2,3).
18.已知点P(2m+4,m-1),请分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3.
(2)点P在第三象限,且点P到两坐标轴的距离之和为12.
(3)点P在坐标轴上.
【练素养】
19.已知当m,n都是实数,且满足2m=8+n时,称p为“开心点”.例如:A(5,3)为“开心点”.
因为当点A为(5,3)时,m-1=5,=3,得m=6,n=4,
所以2m=2×6=12,8+n=8+4=12,
所以2m=8+n.
所以A(5,3)是“开心点”.
(1)判断点B(4,10)是否为“开心点”,并说明理由.
(2)若点M(a,2a-1)是“开心点”,请判断点M在第几象限,并说明理由.
参考答案
【练基础】
1.垂直 重合 数轴 x轴 横轴 向右方向 y轴 纵轴 向上方向 原点 平面
2.C 3.D 4.D
5.(3,2),(2,3),(-2,3),(-1,-3)
【解析】【归纳总结】确定点的坐标的方法:
(1)确定横坐标:从该点向x轴作垂线,垂足对应的x轴上的数为该点的横坐标.(2)确定纵坐标:从该点向y轴作垂线,垂足对应的y轴上的数为该点的纵坐标.
6.C 7.B 8.A 9.一
【练能力】
10.B 【解析】因为点P到x轴的距离为5,所以点P的纵坐标是5或-5.又因为点P的横坐标是-3,所以点P的坐标是(-3,5)或(-3,-5).
11.A
12.D 【解析】由题图知,只有第三象限没有被课本遮挡,故一定没有被课本遮住的点是(-1,-1).
13.-1 2
【解析】由直线AB∥x轴,可知m-1=-2,所以m=-1.由直线AB∥y轴,可知m+1=3,所以m=2.
14.(2,3)(答案不唯一)
【解析】若线段AB与y轴平行,则点B的横坐标与点A的横坐标相同.
15.(4,-2)或(-4,-2)
16.1
【解析】题图中点P的坐标是(4,0).
17.【解析】如图所示.
【归纳总结】在平面直角坐标系中描点(a,b)的方法:①在x轴上找出表示数a的点,过该点作x轴的垂线;②在y轴上找出表示数b的点,过该点作y轴的垂线,两条垂线的交点就是点(a,b).
18.【解析】(1)由题意得m-1-(2m+4)=3,解得m=-8,
∴2m+4=-12,m-1=-9,
∴点P的坐标为(-12,-9).
(2)由题意得|m-1|+|2m+4|=12,2m+4<0,m-1<0,即-(m-1)-(2m+4)=12,解得m=-5,
∴2m+4=-6,m-1=-6,
∴点P的坐标为(-6,-6).
(3)分情况讨论:①当点P在x轴上时,m-1=0,解得m=1,
∴点P的坐标为(6,0);
②当点P在y轴上时,2m+4=0,解得m=-2,
∴点P的坐标为(0,-3).
综上所述,点P的坐标为(6,0)或(0,-3).
【练素养】
19.【解析】(1)(4,10)不是“开心点”,理由如下:
当B(4,10)时,m-1=4,=10,
解得m=5,n=18,
则2m=10,8+n=8+18=26,
所以2m≠8+n,
所以点B(4,10)不是“开心点”.
(2)点M在第三象限,理由如下:
∵点M(a,2a-1)是“开心点”,
∴m-1=a,=2a-1,
∴m=a+1,n=4a-4.
代入2m=8+n,有2a+2=8+4a-4,
∴a=-1,2a-1=-3,
∴M(-1,-3),
故点M在第三象限.
2
