第5章 相交线与平行线 分层作业(含答案) 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 第5章 相交线与平行线 分层作业(含答案) 2023-2024学年初中数学人教版七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 419.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 18:03:47 | ||
图片预览

文档简介
第五章 相交线与平行线 自我评估
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.如图,直线a,b相交于点O,若∠1等于40°,则∠2等于( )
A.50° B.60° C.140° D.160°
2.如图所示的网格中各有不同的图案,不能通过平移得到的是( )
A B C D
3.在如图所示的四个图形中,∠1和∠2是内错角的是( )
A B C D
4.下列说法错误的是( )
A.如果a∥c,b∥c,那么a∥b
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.两点之间的所有连线中,线段最短
D.过一点有且只有一条直线与已知直线平行
5.下列命题中,是假命题的是( )
A.同旁内角互补 B.对顶角相等 C.直角的补角仍然是直角 D.两点之间,线段最短
6.将一块含45°角的直角三角尺ABC按照如图所示的方式放置,点C落在直线a上,点B落在直线b上,直线a∥b,∠1=25°,则∠2的度数是( )
A.15° B.20° C.25° D.30°
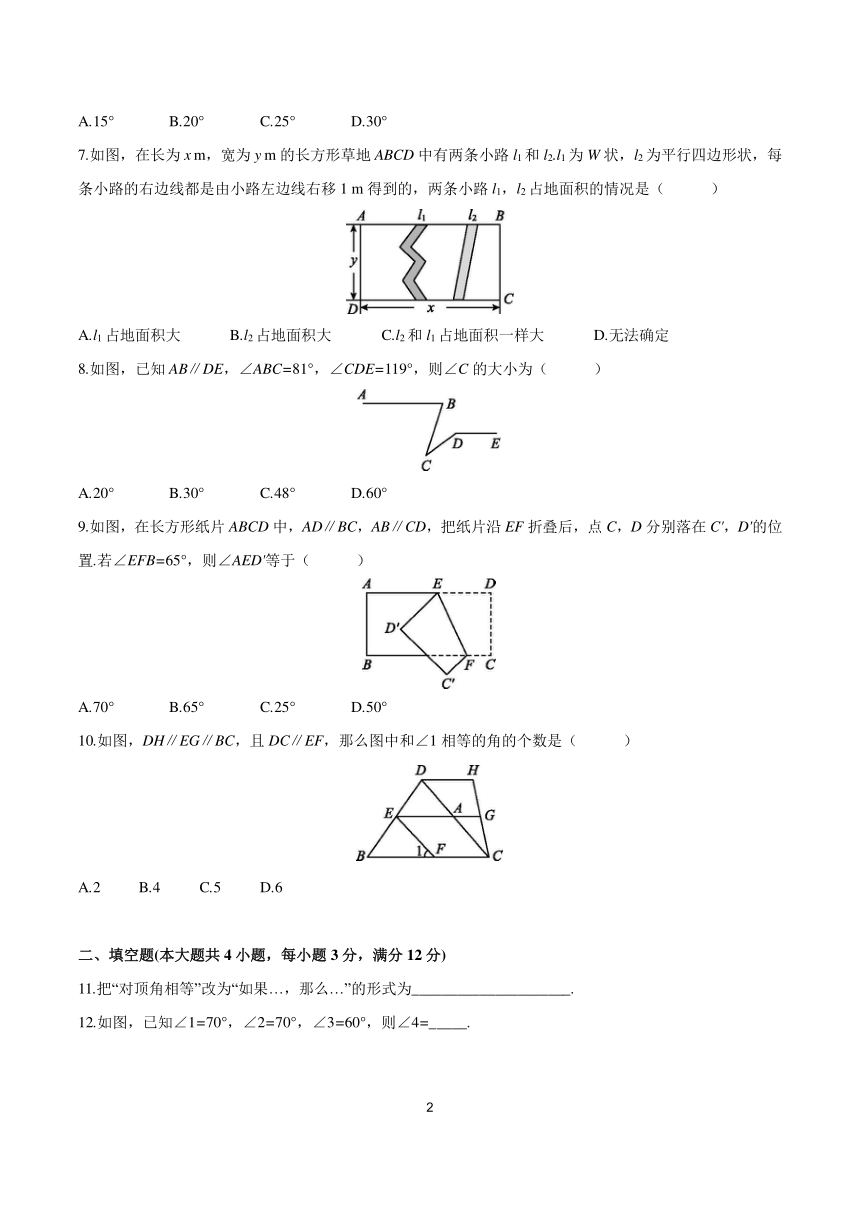
7.如图,在长为x m,宽为y m的长方形草地ABCD中有两条小路l1和l2.l1为W状,l2为平行四边形状,每条小路的右边线都是由小路左边线右移1 m得到的,两条小路l1,l2占地面积的情况是( )
A.l1占地面积大 B.l2占地面积大 C.l2和l1占地面积一样大 D.无法确定
8.如图,已知AB∥DE,∠ABC=81°,∠CDE=119°,则∠C的大小为( )
A.20° B.30° C.48° D.60°
9.如图,在长方形纸片ABCD中,AD∥BC,AB∥CD,把纸片沿EF折叠后,点C,D分别落在C',D'的位置.若∠EFB=65°,则∠AED'等于( )
A.70° B.65° C.25° D.50°
10.如图,DH∥EG∥BC,且DC∥EF,那么图中和∠1相等的角的个数是( )
A.2 B.4 C.5 D.6
二、填空题(本大题共4小题,每小题3分,满分12分)
11.把“对顶角相等”改为“如果…,那么…”的形式为_____________________.
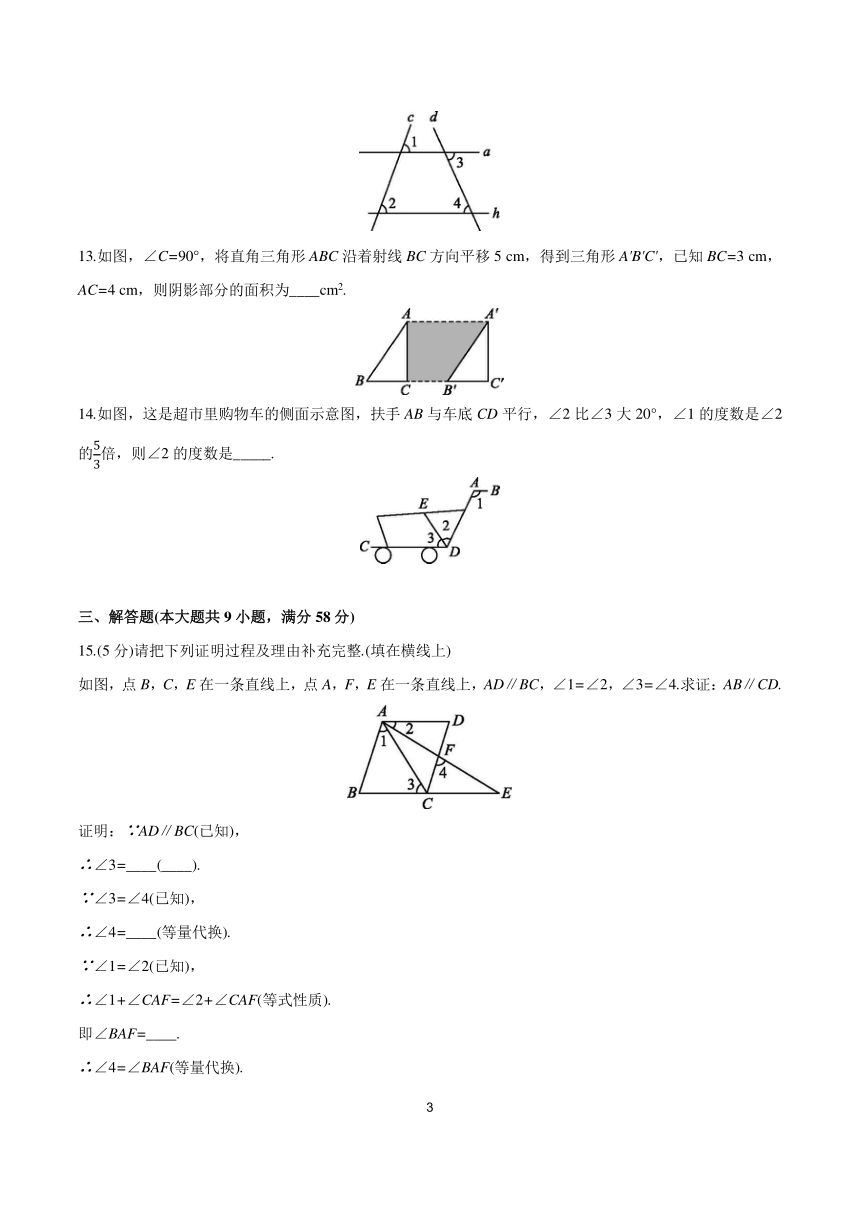
12.如图,已知∠1=70°,∠2=70°,∠3=60°,则∠4=_____.
13.如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移5 cm,得到三角形A'B'C',已知BC=3 cm,AC=4 cm,则阴影部分的面积为____cm2.
14.如图,这是超市里购物车的侧面示意图,扶手AB与车底CD平行,∠2比∠3大20°,∠1的度数是∠2的倍,则∠2的度数是_____.
三、解答题(本大题共9小题,满分58分)
15.(5分)请把下列证明过程及理由补充完整.(填在横线上)
如图,点B,C,E在一条直线上,点A,F,E在一条直线上,AD∥BC,∠1=∠2,∠3=∠4.求证:AB∥CD.
证明:∵AD∥BC(已知),
∴∠3=____(____).
∵∠3=∠4(已知),
∴∠4=____(等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式性质).
即∠BAF=____.
∴∠4=∠BAF(等量代换).
∴AB∥CD(____).
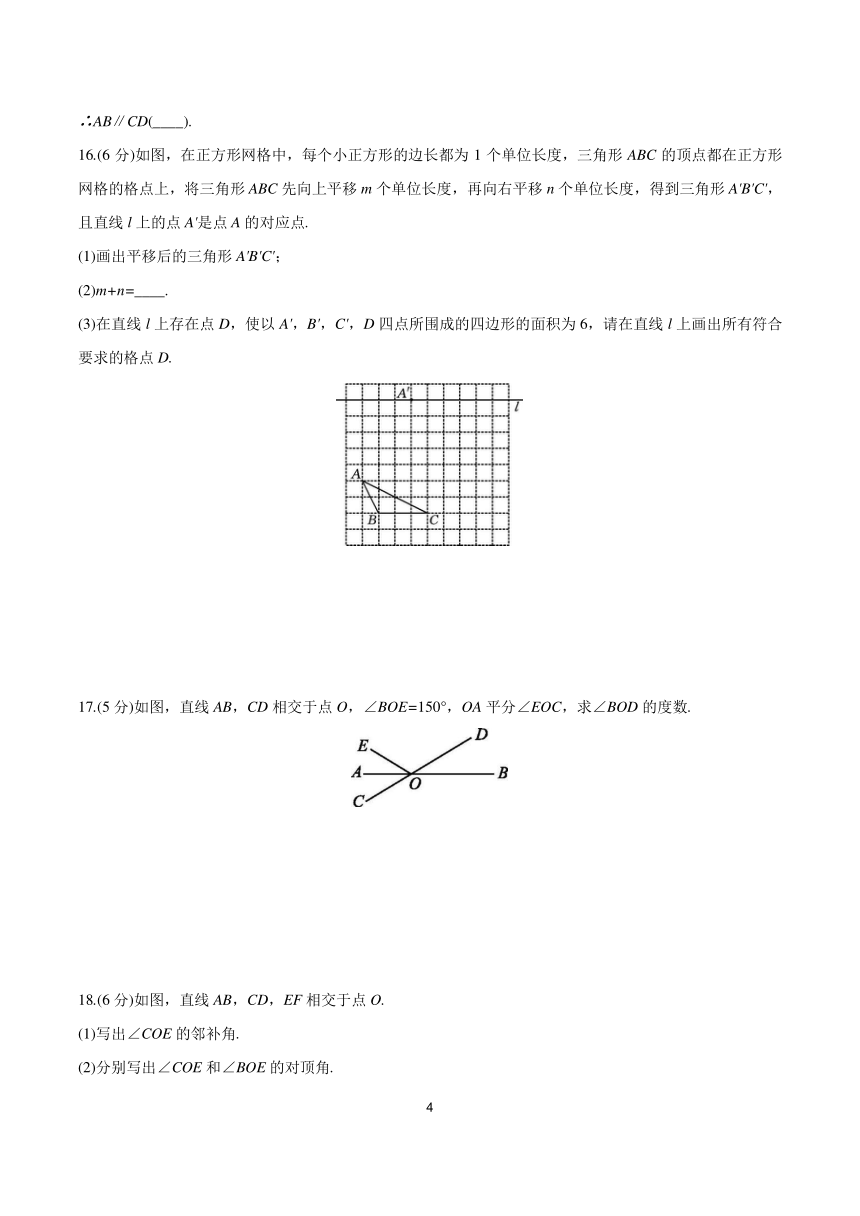
16.(6分)如图,在正方形网格中,每个小正方形的边长都为1个单位长度,三角形ABC的顶点都在正方形网格的格点上,将三角形ABC先向上平移m个单位长度,再向右平移n个单位长度,得到三角形A'B'C',且直线l上的点A'是点A的对应点.
(1)画出平移后的三角形A'B'C';
(2)m+n=____.
(3)在直线l上存在点D,使以A',B',C',D四点所围成的四边形的面积为6,请在直线l上画出所有符合要求的格点D.
17.(5分)如图,直线AB,CD相交于点O,∠BOE=150°,OA平分∠EOC,求∠BOD的度数.
18.(6分)如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角.
(2)分别写出∠COE和∠BOE的对顶角.
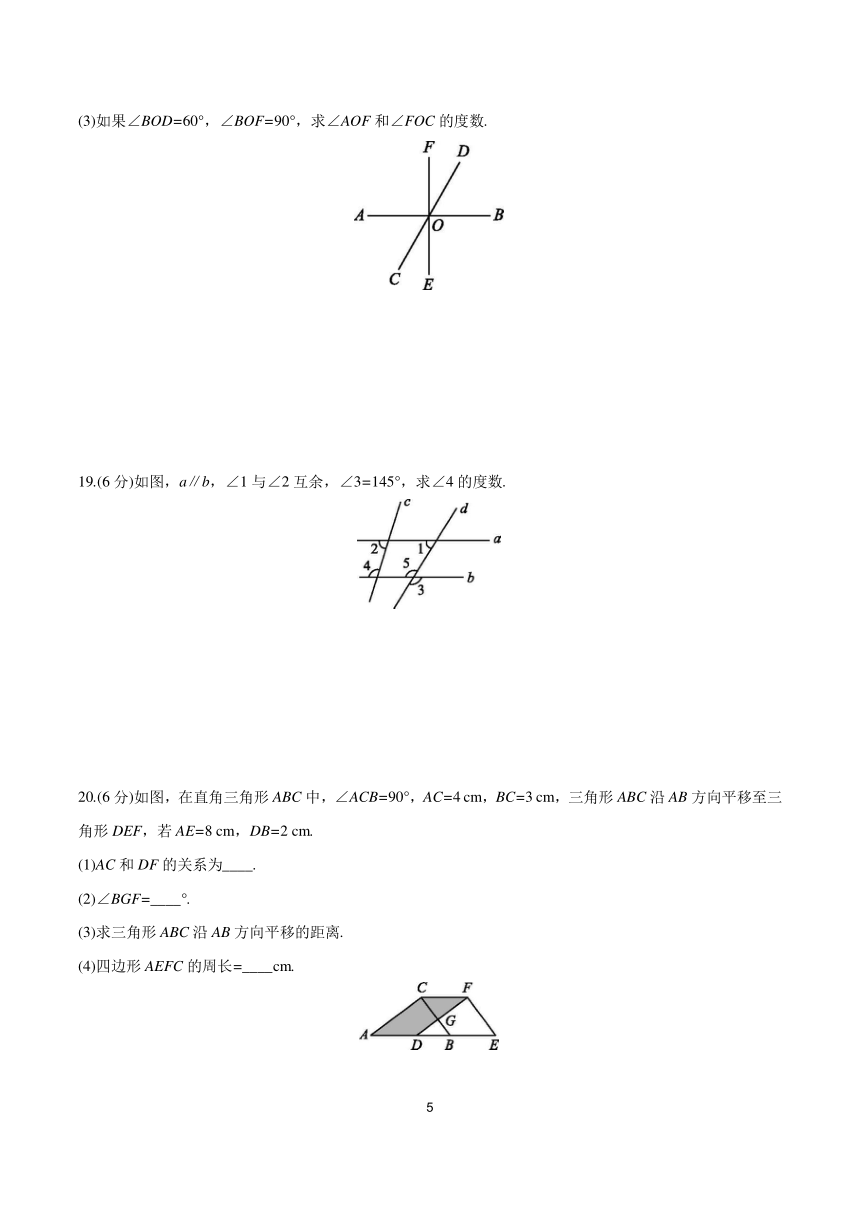
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
19.(6分)如图,a∥b,∠1与∠2互余,∠3=145°,求∠4的度数.
20.(6分)如图,在直角三角形ABC中,∠ACB=90°,AC=4 cm,BC=3 cm,三角形ABC沿AB方向平移至三角形DEF,若AE=8 cm,DB=2 cm.
(1)AC和DF的关系为____.
(2)∠BGF=____°.
(3)求三角形ABC沿AB方向平移的距离.
(4)四边形AEFC的周长=____cm.
21.(7分)探究:如图1,直线AB,BC,AC两两相交,交点分别为点A,B,C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=40°,求∠DEF的度数.
请将下面的解答过程补充完整.
解:∵DE∥BC(已知),
∴____(两直线平行,内错角相等).
∵EF∥AB(已知),
∴∠ABC=∠EFC(____),
∴∠DEF=∠ABC=40°(等量代换).
应用:如图2,直线AB,BC,AC两两相交,交点分别为点A,B,C,点D在线段AB的延长线上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,若∠ABC=50°,求∠DEF的度数.
22.(8分)【新风向·探究性试题】
(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
(2)如图2,AD∥BC,点P在射线OM上运动,若∠ADP=∠α,∠BCP=∠β.
①当点P在A,B两点之间运动时,∠CPD,∠α,∠β之间的数量关系为____________.
②当点P在A,B两点外侧运动时(点P与点A,B,O三点不重合),请写出∠CPD,∠α,∠β之间的数量关系,并说明理由.
图1 图2
备用图
23.(9分)已知直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD.
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM.
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取一点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠GHM的度数.
参考答案
1.C 2.C 3.B 4.D 5.A 6.B 7.C 8.A 9.D
10.C
11.如果两个角互为对顶角,那么这两个角相等.
12.60°
13.14
14.60°
15.【解析】∠CAD;两直线平行,内错角相等;∠CAD;∠CAD;同位角相等,两直线平行.
16.【解析】(1)如图,三角形A'B'C'即所求.
(2)8.
(3)如图所示,点D1,D2即所求.
17.【解析】∵∠BOE=150°,∴∠AOE=30°.
∵OA平分∠COE,∴∠AOC=∠AOE=30°.
∵∠BOD与∠AOC是对顶角,∴∠BOD=∠AOC=30°.
18.【解析】(1)∠COE的邻补角:∠DOE,∠COF.
(2)∠COE的对顶角是∠DOF;∠BOE的对顶角是∠AOF.
(3)∵邻补角互补,∠BOF=90°,
∴∠AOF=90°.
∵∠BOD=60°,
∴∠AOC=60°,
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
19.【解析】∵∠3=145°,
∴∠5=∠3=145°.
∵a∥b,∴∠1+∠5=180°,
∴∠1=35°.
∵∠1与∠2互余,
∴∠2=55°.
∵a∥b,
∴∠2+∠4=180°,
∴∠4=125°.
20.【解析】(1)AC=DF,且AC∥DF.
(2)90.
(3)由平移得AD=BE.
∵AE=8 cm,DB=2 cm,
∴AD=BE==3(cm),
∴平移的距离为3 cm.
(4)18.
21.【解析】探究:∠DEF=∠EFC;两直线平行,同位角相等.
应用:∵DE∥BC,∴∠ABC=∠ADE=50°(两直线平行,同位角相等).
∵EF∥AB,
∴∠ADE+∠DEF=180°(两直线平行,同旁内角互补),
∴∠DEF=180°-50°=130°.
22.【解析】
(1)如图1,过点P作PQ∥AB,
∴∠APQ+∠PAB=180°.
∵AB∥CD,∴PQ∥CD,
∴∠CPQ+∠PCD=180°.
∵∠PAB=130°,∠PCD=120°,
∴∠APQ=180°-∠PAB=50°,
∠CPQ=180°-∠PCD=60°,
∴∠APC=∠APQ+∠CPQ=50°+60°=110°.
(2)①∠CPD=∠α+∠β.
提示:如图2,过点P作PE∥AD交ON于点E,
∵PE∥AD,AD∥BC,
∴∠α=∠DPE,PE∥BC,
∴∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β.
②∠CPD=∠β-∠α或∠CPD=∠α-∠β.
理由:当点P在BA的延长线上时,
如图3,过点P作PH∥AD交ON于点H,
∵PH∥AD,AD∥BC,
∴∠α=∠DPH,PH∥BC,
∴∠β=∠CPH,
∴∠CPD=∠CPH-∠DPH=∠β-∠α.
当点P在B,O两点之间时,
如图4,过点P作PF∥AD交ON于点F,
∵PF∥AD,AD∥BC,
∴∠α=∠DPF,PF∥BC,
∴∠β=∠CPF,
∴∠CPD=∠DPF-∠CPF=∠α-∠β.
图2 图3
图4
23.【解析】(1)证明:∵∠AGE+∠DHE=180°,∠AGE=∠BGF,
∴∠BGF+∠DHE=180°,∴AB∥CD.
(2)
图1
证明:如图1,过点M作MR∥AB.
又∵AB∥CD,
∴AB∥CD∥MR,
∴∠GMR=∠AGM,∠HMR=∠CHM,
∴∠GMH=∠GMR+∠HMR=∠AGM+∠CHM.
(3)如图2,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β.
图2
∵射线GH是∠BGM的平分线,
∴∠FGM=∠BGM=(180°-∠AGM)=90°-α,
∴∠AGH=∠AGM+∠FGM=2α+90°-α=90°+α.
∵∠M=∠N+∠FGN,
∴2α+β=2α+∠FGN,
∴∠FGN=2β.
过点H作HT∥GN,则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∴∠CHG=∠CHM+∠GHM=β+2α+2β=2α+3β.
∵AB∥CD,
∴∠AGH+∠CHG=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
2
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.如图,直线a,b相交于点O,若∠1等于40°,则∠2等于( )
A.50° B.60° C.140° D.160°
2.如图所示的网格中各有不同的图案,不能通过平移得到的是( )
A B C D
3.在如图所示的四个图形中,∠1和∠2是内错角的是( )
A B C D
4.下列说法错误的是( )
A.如果a∥c,b∥c,那么a∥b
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.两点之间的所有连线中,线段最短
D.过一点有且只有一条直线与已知直线平行
5.下列命题中,是假命题的是( )
A.同旁内角互补 B.对顶角相等 C.直角的补角仍然是直角 D.两点之间,线段最短
6.将一块含45°角的直角三角尺ABC按照如图所示的方式放置,点C落在直线a上,点B落在直线b上,直线a∥b,∠1=25°,则∠2的度数是( )
A.15° B.20° C.25° D.30°
7.如图,在长为x m,宽为y m的长方形草地ABCD中有两条小路l1和l2.l1为W状,l2为平行四边形状,每条小路的右边线都是由小路左边线右移1 m得到的,两条小路l1,l2占地面积的情况是( )
A.l1占地面积大 B.l2占地面积大 C.l2和l1占地面积一样大 D.无法确定
8.如图,已知AB∥DE,∠ABC=81°,∠CDE=119°,则∠C的大小为( )
A.20° B.30° C.48° D.60°
9.如图,在长方形纸片ABCD中,AD∥BC,AB∥CD,把纸片沿EF折叠后,点C,D分别落在C',D'的位置.若∠EFB=65°,则∠AED'等于( )
A.70° B.65° C.25° D.50°
10.如图,DH∥EG∥BC,且DC∥EF,那么图中和∠1相等的角的个数是( )
A.2 B.4 C.5 D.6
二、填空题(本大题共4小题,每小题3分,满分12分)
11.把“对顶角相等”改为“如果…,那么…”的形式为_____________________.
12.如图,已知∠1=70°,∠2=70°,∠3=60°,则∠4=_____.
13.如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移5 cm,得到三角形A'B'C',已知BC=3 cm,AC=4 cm,则阴影部分的面积为____cm2.
14.如图,这是超市里购物车的侧面示意图,扶手AB与车底CD平行,∠2比∠3大20°,∠1的度数是∠2的倍,则∠2的度数是_____.
三、解答题(本大题共9小题,满分58分)
15.(5分)请把下列证明过程及理由补充完整.(填在横线上)
如图,点B,C,E在一条直线上,点A,F,E在一条直线上,AD∥BC,∠1=∠2,∠3=∠4.求证:AB∥CD.
证明:∵AD∥BC(已知),
∴∠3=____(____).
∵∠3=∠4(已知),
∴∠4=____(等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式性质).
即∠BAF=____.
∴∠4=∠BAF(等量代换).
∴AB∥CD(____).
16.(6分)如图,在正方形网格中,每个小正方形的边长都为1个单位长度,三角形ABC的顶点都在正方形网格的格点上,将三角形ABC先向上平移m个单位长度,再向右平移n个单位长度,得到三角形A'B'C',且直线l上的点A'是点A的对应点.
(1)画出平移后的三角形A'B'C';
(2)m+n=____.
(3)在直线l上存在点D,使以A',B',C',D四点所围成的四边形的面积为6,请在直线l上画出所有符合要求的格点D.
17.(5分)如图,直线AB,CD相交于点O,∠BOE=150°,OA平分∠EOC,求∠BOD的度数.
18.(6分)如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角.
(2)分别写出∠COE和∠BOE的对顶角.
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
19.(6分)如图,a∥b,∠1与∠2互余,∠3=145°,求∠4的度数.
20.(6分)如图,在直角三角形ABC中,∠ACB=90°,AC=4 cm,BC=3 cm,三角形ABC沿AB方向平移至三角形DEF,若AE=8 cm,DB=2 cm.
(1)AC和DF的关系为____.
(2)∠BGF=____°.
(3)求三角形ABC沿AB方向平移的距离.
(4)四边形AEFC的周长=____cm.
21.(7分)探究:如图1,直线AB,BC,AC两两相交,交点分别为点A,B,C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=40°,求∠DEF的度数.
请将下面的解答过程补充完整.
解:∵DE∥BC(已知),
∴____(两直线平行,内错角相等).
∵EF∥AB(已知),
∴∠ABC=∠EFC(____),
∴∠DEF=∠ABC=40°(等量代换).
应用:如图2,直线AB,BC,AC两两相交,交点分别为点A,B,C,点D在线段AB的延长线上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,若∠ABC=50°,求∠DEF的度数.
22.(8分)【新风向·探究性试题】
(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
(2)如图2,AD∥BC,点P在射线OM上运动,若∠ADP=∠α,∠BCP=∠β.
①当点P在A,B两点之间运动时,∠CPD,∠α,∠β之间的数量关系为____________.
②当点P在A,B两点外侧运动时(点P与点A,B,O三点不重合),请写出∠CPD,∠α,∠β之间的数量关系,并说明理由.
图1 图2
备用图
23.(9分)已知直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD.
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM.
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取一点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠GHM的度数.
参考答案
1.C 2.C 3.B 4.D 5.A 6.B 7.C 8.A 9.D
10.C
11.如果两个角互为对顶角,那么这两个角相等.
12.60°
13.14
14.60°
15.【解析】∠CAD;两直线平行,内错角相等;∠CAD;∠CAD;同位角相等,两直线平行.
16.【解析】(1)如图,三角形A'B'C'即所求.
(2)8.
(3)如图所示,点D1,D2即所求.
17.【解析】∵∠BOE=150°,∴∠AOE=30°.
∵OA平分∠COE,∴∠AOC=∠AOE=30°.
∵∠BOD与∠AOC是对顶角,∴∠BOD=∠AOC=30°.
18.【解析】(1)∠COE的邻补角:∠DOE,∠COF.
(2)∠COE的对顶角是∠DOF;∠BOE的对顶角是∠AOF.
(3)∵邻补角互补,∠BOF=90°,
∴∠AOF=90°.
∵∠BOD=60°,
∴∠AOC=60°,
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
19.【解析】∵∠3=145°,
∴∠5=∠3=145°.
∵a∥b,∴∠1+∠5=180°,
∴∠1=35°.
∵∠1与∠2互余,
∴∠2=55°.
∵a∥b,
∴∠2+∠4=180°,
∴∠4=125°.
20.【解析】(1)AC=DF,且AC∥DF.
(2)90.
(3)由平移得AD=BE.
∵AE=8 cm,DB=2 cm,
∴AD=BE==3(cm),
∴平移的距离为3 cm.
(4)18.
21.【解析】探究:∠DEF=∠EFC;两直线平行,同位角相等.
应用:∵DE∥BC,∴∠ABC=∠ADE=50°(两直线平行,同位角相等).
∵EF∥AB,
∴∠ADE+∠DEF=180°(两直线平行,同旁内角互补),
∴∠DEF=180°-50°=130°.
22.【解析】
(1)如图1,过点P作PQ∥AB,
∴∠APQ+∠PAB=180°.
∵AB∥CD,∴PQ∥CD,
∴∠CPQ+∠PCD=180°.
∵∠PAB=130°,∠PCD=120°,
∴∠APQ=180°-∠PAB=50°,
∠CPQ=180°-∠PCD=60°,
∴∠APC=∠APQ+∠CPQ=50°+60°=110°.
(2)①∠CPD=∠α+∠β.
提示:如图2,过点P作PE∥AD交ON于点E,
∵PE∥AD,AD∥BC,
∴∠α=∠DPE,PE∥BC,
∴∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β.
②∠CPD=∠β-∠α或∠CPD=∠α-∠β.
理由:当点P在BA的延长线上时,
如图3,过点P作PH∥AD交ON于点H,
∵PH∥AD,AD∥BC,
∴∠α=∠DPH,PH∥BC,
∴∠β=∠CPH,
∴∠CPD=∠CPH-∠DPH=∠β-∠α.
当点P在B,O两点之间时,
如图4,过点P作PF∥AD交ON于点F,
∵PF∥AD,AD∥BC,
∴∠α=∠DPF,PF∥BC,
∴∠β=∠CPF,
∴∠CPD=∠DPF-∠CPF=∠α-∠β.
图2 图3
图4
23.【解析】(1)证明:∵∠AGE+∠DHE=180°,∠AGE=∠BGF,
∴∠BGF+∠DHE=180°,∴AB∥CD.
(2)
图1
证明:如图1,过点M作MR∥AB.
又∵AB∥CD,
∴AB∥CD∥MR,
∴∠GMR=∠AGM,∠HMR=∠CHM,
∴∠GMH=∠GMR+∠HMR=∠AGM+∠CHM.
(3)如图2,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β.
图2
∵射线GH是∠BGM的平分线,
∴∠FGM=∠BGM=(180°-∠AGM)=90°-α,
∴∠AGH=∠AGM+∠FGM=2α+90°-α=90°+α.
∵∠M=∠N+∠FGN,
∴2α+β=2α+∠FGN,
∴∠FGN=2β.
过点H作HT∥GN,则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∴∠CHG=∠CHM+∠GHM=β+2α+2β=2α+3β.
∵AB∥CD,
∴∠AGH+∠CHG=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
2
