第6章 实数 分层作业 (含答案)2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 第6章 实数 分层作业 (含答案)2023-2024学年初中数学人教版七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 89.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 18:06:43 | ||
图片预览



文档简介
第六章 实数 自我评估
(建议用时:90分钟 分值:120分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.的平方根是( )
A.± B. C.- D.±4
2.下列各数:1.414,,-,0.其中是无理数的是( )
A.1.414 B. C.- D.0
3.在实数-,-2,0,中,最小的实数是( )
A.-2 B.0 C.- D.
4.估计的值在( )
A.4和5之间 B.5和6之间 C.6和7之间 D.7和8之间
5.已知a2=4,=-2,则a+b的值为( )
A.10 B.6 C.-6 D.-10或-6
6.已知一个正方体的表面积为12 dm2,则这个正方体的棱长为( )
A.1 dm B. dm C. dm D.3 dm
7.如图,在数轴上表示实数的可能是点( )
A.P B.Q C.M D.N
8.下列说法:①-3是的平方根;②-7是(-7)2的算术平方根;③125的立方根是±5;④-16的平方根是±4;⑤0没有算术平方根.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.已知x是(-)2的平方根,y是64的立方根,则x+y的值为( )
A.3 B.7 C.3或7 D.1或7
10.已知边长为m的正方形的面积为12,则下列关于m的说法:①m是无理数;②m是方程m2-12=0的一个解;③m是12的算术平方根.其中错误的有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本大题共6小题,每小题3分,满分18分)
11.计算:|-3|=_____.
12.在数轴上到原点的距离等于的所有点所表示的数是_____.
13.如图,数轴上A,B两点之间表示整数的点有_____个.
14.一个数值转换器,原理如图所示.当输入x为512时,输出y的值是_____.
15.【新风向·开放性试题】请写出一个大于且小于3的无理数:_______.
16.【新风向·新定义试题】对任意两个实数a,b定义两种运算:a@b=a b=并且定义运算顺序仍然是先做括号内的,例如(-2)@3=3,(-2) 3=-2,[(-2)@3] 2=2.那么(@2) =_____.
三、解答题(本大题共11小题,满分72分)
17.(每小题2分,共6分)计算:
(1)+-.
(2)3-2(-1).
(3)|3-3|-3-.
18.(每小题3分,共6分)求下列各式中x的值:
(1)(x+2)3+1=.
(2)25(x2-1)=24.
19.(5分)根据下表回答问题:
x 16 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 17
x2 256 259.21 262.44 265.69 268.96 272.25 275.56 278.89 282.24 285.61 289
(1)=____;≈____.
(2)272.25的平方根是____.
(3)若a,b是表中两个相邻的数,a<20.(5分)如图,一只蜗牛从点A出发,沿着数轴向右爬3个单位长度到达点B,若点B表示的数是,设点A所表示的数为a.
(1)求a的值.
(2)求|a-1|+|3+a|的值.
21.(6分)若实数m的两个平方根是4a+21和a-6,b的立方根是-2,求m+3a+b的算术平方根.
22.(6分)比较大小:
(1)与4.7.
(2)与1+.
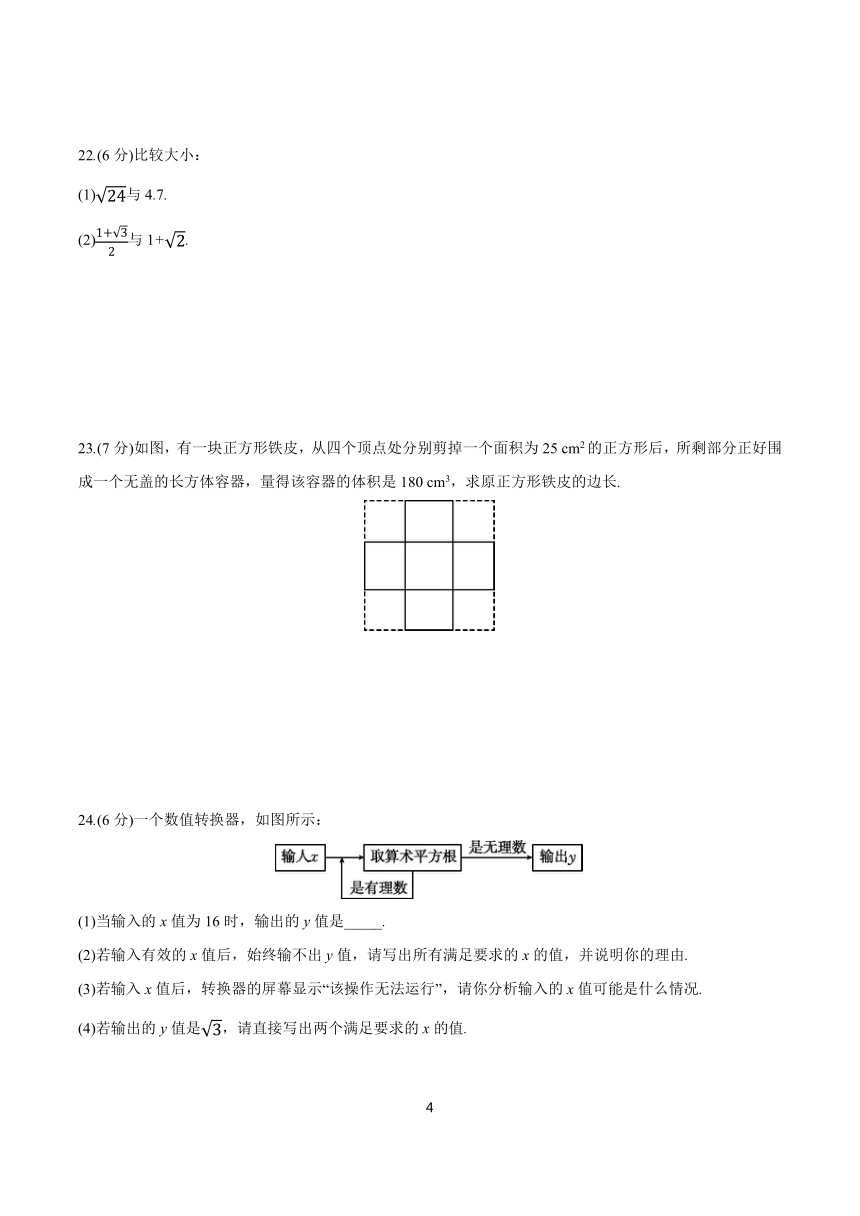
23.(7分)如图,有一块正方形铁皮,从四个顶点处分别剪掉一个面积为25 cm2的正方形后,所剩部分正好围成一个无盖的长方体容器,量得该容器的体积是180 cm3,求原正方形铁皮的边长.
24.(6分)一个数值转换器,如图所示:
(1)当输入的x值为16时,输出的y值是_____.
(2)若输入有效的x值后,始终输不出y值,请写出所有满足要求的x的值,并说明你的理由.
(3)若输入x值后,转换器的屏幕显示“该操作无法运行”,请你分析输入的x值可能是什么情况.
(4)若输出的y值是,请直接写出两个满足要求的x的值.
25.(8分)用“*”表示一种新的运算,对于正实数a,b,都有a*b=+b,例如:25*8=+8=13.
(1)求1*5的值.
(2)若16*(m3-1)=11,求m的值
26.(8分)在一次“智慧课堂”教学比赛的课堂上,李老师说:“是无理数,无理数就是无限不循环小数,同学们,你能把的小数部分全部写出来吗 ”大家议论纷纷,张晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(-1)表示它的小数部分.”李老师说:“张晶同学的说法是正确的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.”请你解答:已知8+=x+y,其中x是一个整数,且027.(9分)【新风向·探究性试题】有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程.
(1)解题与归纳:
①小明摘选了以下各题,请你帮他完成填空.
=___;=___;=___;=___;=___;=___.
②归纳:对于任意实数a,
有=_____=
③小芳摘选了以下各题,请你帮她完成填空.
()2=___;()2=___;()2=____;()2=____;()2=____;()2=___.
④归纳:对于任意非负实数a,有()2=___.
(2)应用:根据他们归纳得出的结论,解答问题.
数a,b在数轴上的位置如图所示,化简:---()2.
参考答案
1.A 2.B 3.A 4.C 5.D 6.B 7.C 8.A 9.D
10.A 11.3- 12.± 13.4 14. 15.(答案不唯一)
16.
17.【解析】(1)原式=0.3+2-=1.8.
(2)原式=3-2+2=+2.
(3)原式=3-3-3-5=-8.
18.【解析】(1)(x+2)3=-,
x+2=-,x=-.
(2)x2-1=,x2=,
x=或x=-.
19.【解析】(1)16;16.(2)±16.5.(3)16.7;16.8.
20.【解析】(1)由题可得a=-3.
(2)把a的值代入,得|a-1|+|3+a|=|-3-1|+|3+-3|=4-+=4.
21.【解析】因为b的立方根是-2,
所以b=-8.
又因为实数m的两个平方根是4a+21和a-6,
所以4a+21+a-6=0,
解得a=-3.当a=-3时,4a+21=9,a-6=-9,此时m=81,
所以m+3a+b=81-9-8=64,
所以m+3a+b的算术平方根是=8.
22.【解析】(1)∵4.72=22.09,24>22.09,
∴>4.7.
(2)∵1<<2,1<<2,
∴2<1+<3,2<1+<3,
∴1<<1.5,
∴<1+.
23.【解析】∵从四个顶点处分别剪掉一个面积为25 cm2的正方形,
∴剪掉的正方形边长为5 cm.
设原来正方形的边长为x cm,
由题意可得5(x-10)2=180,
∴(x-10)2=36,
x-10=6或x-10=-6,
解得x=16或x=4(不符合题意,舍去),
∴原来正方形的边长为16 cm.
24.【解析】(1).
解法提示:因为16的算术平方根是4,4是有理数,所以4不能输出.
因为4的算术平方根是2,2是有理数,所以2不能输出.
因为2的算术平方根是,是无理数,故输出.
(2)0,1.
理由:因为0和1的算术平方根是它们本身,0和1是有理数,
所以当x为0或1时,始终输不出y值.
(3)x<0.
当x<0时,导致开平方运算无法进行.
(4)3或9.(答案不唯一)
25.【解析】(1)∵a*b=+b,
∴1*5=+5=1+5=6.
(2)∵a*b=+b,16*(m3-1)=11,
∴+(m3-1)=11,
即4+m3-1=11,
∴m3=8,∴m=2.
26.【解析】∵1<<2,
∴9<8+<10.
∵8+=x+y,其中x是一个整数,且0∴x=9,y=8+-9=-1,
∴2x+(-y)2026=2×9+[-(-1)]2026=18+1=19.
27.【解析】(1)①2 5 6 0 3 6
②|a| a 0 -a
③4 9 25 36 49 0 a
(2)由题中数轴,得a<0,b>0,b>a,所以b-a>0,
原式=|a|-|b|-|a-b|-(b-a)
=-a-b+(a-b)-(b-a)
=-a-b+a-b-b+a
=a-3b.
2
(建议用时:90分钟 分值:120分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.的平方根是( )
A.± B. C.- D.±4
2.下列各数:1.414,,-,0.其中是无理数的是( )
A.1.414 B. C.- D.0
3.在实数-,-2,0,中,最小的实数是( )
A.-2 B.0 C.- D.
4.估计的值在( )
A.4和5之间 B.5和6之间 C.6和7之间 D.7和8之间
5.已知a2=4,=-2,则a+b的值为( )
A.10 B.6 C.-6 D.-10或-6
6.已知一个正方体的表面积为12 dm2,则这个正方体的棱长为( )
A.1 dm B. dm C. dm D.3 dm
7.如图,在数轴上表示实数的可能是点( )
A.P B.Q C.M D.N
8.下列说法:①-3是的平方根;②-7是(-7)2的算术平方根;③125的立方根是±5;④-16的平方根是±4;⑤0没有算术平方根.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.已知x是(-)2的平方根,y是64的立方根,则x+y的值为( )
A.3 B.7 C.3或7 D.1或7
10.已知边长为m的正方形的面积为12,则下列关于m的说法:①m是无理数;②m是方程m2-12=0的一个解;③m是12的算术平方根.其中错误的有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本大题共6小题,每小题3分,满分18分)
11.计算:|-3|=_____.
12.在数轴上到原点的距离等于的所有点所表示的数是_____.
13.如图,数轴上A,B两点之间表示整数的点有_____个.
14.一个数值转换器,原理如图所示.当输入x为512时,输出y的值是_____.
15.【新风向·开放性试题】请写出一个大于且小于3的无理数:_______.
16.【新风向·新定义试题】对任意两个实数a,b定义两种运算:a@b=a b=并且定义运算顺序仍然是先做括号内的,例如(-2)@3=3,(-2) 3=-2,[(-2)@3] 2=2.那么(@2) =_____.
三、解答题(本大题共11小题,满分72分)
17.(每小题2分,共6分)计算:
(1)+-.
(2)3-2(-1).
(3)|3-3|-3-.
18.(每小题3分,共6分)求下列各式中x的值:
(1)(x+2)3+1=.
(2)25(x2-1)=24.
19.(5分)根据下表回答问题:
x 16 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 17
x2 256 259.21 262.44 265.69 268.96 272.25 275.56 278.89 282.24 285.61 289
(1)=____;≈____.
(2)272.25的平方根是____.
(3)若a,b是表中两个相邻的数,a<
(1)求a的值.
(2)求|a-1|+|3+a|的值.
21.(6分)若实数m的两个平方根是4a+21和a-6,b的立方根是-2,求m+3a+b的算术平方根.
22.(6分)比较大小:
(1)与4.7.
(2)与1+.
23.(7分)如图,有一块正方形铁皮,从四个顶点处分别剪掉一个面积为25 cm2的正方形后,所剩部分正好围成一个无盖的长方体容器,量得该容器的体积是180 cm3,求原正方形铁皮的边长.
24.(6分)一个数值转换器,如图所示:
(1)当输入的x值为16时,输出的y值是_____.
(2)若输入有效的x值后,始终输不出y值,请写出所有满足要求的x的值,并说明你的理由.
(3)若输入x值后,转换器的屏幕显示“该操作无法运行”,请你分析输入的x值可能是什么情况.
(4)若输出的y值是,请直接写出两个满足要求的x的值.
25.(8分)用“*”表示一种新的运算,对于正实数a,b,都有a*b=+b,例如:25*8=+8=13.
(1)求1*5的值.
(2)若16*(m3-1)=11,求m的值
26.(8分)在一次“智慧课堂”教学比赛的课堂上,李老师说:“是无理数,无理数就是无限不循环小数,同学们,你能把的小数部分全部写出来吗 ”大家议论纷纷,张晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(-1)表示它的小数部分.”李老师说:“张晶同学的说法是正确的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.”请你解答:已知8+=x+y,其中x是一个整数,且0
(1)解题与归纳:
①小明摘选了以下各题,请你帮他完成填空.
=___;=___;=___;=___;=___;=___.
②归纳:对于任意实数a,
有=_____=
③小芳摘选了以下各题,请你帮她完成填空.
()2=___;()2=___;()2=____;()2=____;()2=____;()2=___.
④归纳:对于任意非负实数a,有()2=___.
(2)应用:根据他们归纳得出的结论,解答问题.
数a,b在数轴上的位置如图所示,化简:---()2.
参考答案
1.A 2.B 3.A 4.C 5.D 6.B 7.C 8.A 9.D
10.A 11.3- 12.± 13.4 14. 15.(答案不唯一)
16.
17.【解析】(1)原式=0.3+2-=1.8.
(2)原式=3-2+2=+2.
(3)原式=3-3-3-5=-8.
18.【解析】(1)(x+2)3=-,
x+2=-,x=-.
(2)x2-1=,x2=,
x=或x=-.
19.【解析】(1)16;16.(2)±16.5.(3)16.7;16.8.
20.【解析】(1)由题可得a=-3.
(2)把a的值代入,得|a-1|+|3+a|=|-3-1|+|3+-3|=4-+=4.
21.【解析】因为b的立方根是-2,
所以b=-8.
又因为实数m的两个平方根是4a+21和a-6,
所以4a+21+a-6=0,
解得a=-3.当a=-3时,4a+21=9,a-6=-9,此时m=81,
所以m+3a+b=81-9-8=64,
所以m+3a+b的算术平方根是=8.
22.【解析】(1)∵4.72=22.09,24>22.09,
∴>4.7.
(2)∵1<<2,1<<2,
∴2<1+<3,2<1+<3,
∴1<<1.5,
∴<1+.
23.【解析】∵从四个顶点处分别剪掉一个面积为25 cm2的正方形,
∴剪掉的正方形边长为5 cm.
设原来正方形的边长为x cm,
由题意可得5(x-10)2=180,
∴(x-10)2=36,
x-10=6或x-10=-6,
解得x=16或x=4(不符合题意,舍去),
∴原来正方形的边长为16 cm.
24.【解析】(1).
解法提示:因为16的算术平方根是4,4是有理数,所以4不能输出.
因为4的算术平方根是2,2是有理数,所以2不能输出.
因为2的算术平方根是,是无理数,故输出.
(2)0,1.
理由:因为0和1的算术平方根是它们本身,0和1是有理数,
所以当x为0或1时,始终输不出y值.
(3)x<0.
当x<0时,导致开平方运算无法进行.
(4)3或9.(答案不唯一)
25.【解析】(1)∵a*b=+b,
∴1*5=+5=1+5=6.
(2)∵a*b=+b,16*(m3-1)=11,
∴+(m3-1)=11,
即4+m3-1=11,
∴m3=8,∴m=2.
26.【解析】∵1<<2,
∴9<8+<10.
∵8+=x+y,其中x是一个整数,且0
∴2x+(-y)2026=2×9+[-(-1)]2026=18+1=19.
27.【解析】(1)①2 5 6 0 3 6
②|a| a 0 -a
③4 9 25 36 49 0 a
(2)由题中数轴,得a<0,b>0,b>a,所以b-a>0,
原式=|a|-|b|-|a-b|-(b-a)
=-a-b+(a-b)-(b-a)
=-a-b+a-b-b+a
=a-3b.
2
