第7章 平面直角坐标系 分层作业(含答案) 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 第7章 平面直角坐标系 分层作业(含答案) 2023-2024学年初中数学人教版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 534.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 18:06:18 | ||
图片预览




文档简介
第七章 平面直角坐标系 自我评估
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.平面直角坐标系中,和有序实数对一一对应的是( )
A.x轴上的点 B.y轴上的点
C.平面直角坐标系内的点 D.x轴和y轴上的点
2.点P(5,-3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.坐标为(x,x-1)的点一定不会在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点A(3,1),B(2,2),则“宝藏”点C的位置是( )
A.(1,0) B.(1,2) C.(2,1) D.(1,1)
5.若点P在第四象限,且到x轴的距离是2,到y轴的距离是4,则P点的坐标为( )
A.(2,4) B.(-4,2) C.(4,-2) D.(-2,4)
6.小李在平面直角坐标系中画了一张示意图,分别标出了学校、电影院、体育馆、超市的大致位置.如果张大妈从体育馆向南走150米,再向东走400米,再向南走250米,再向西走50米,最终到达的地点是( )
A.学校 B.电影院 C.体育馆 D.超市
7.在平面直角坐标系中,点A,B的坐标分别为(1,0),(3,2),连接AB,将线段AB平移后得到线段A'B',点A的对应点A'坐标为(2,1),则点B'坐标为( )
A.(4,2) B.(4,3) C.(6,2) D.(6,3)
8.下列语句,其中正确的有( )
①点(3,2)与(2,3)是同一个点;②点(0,-2)在x轴上;③点(0,0)是坐标原点;④点(-2,-6)在第三象限内.
A.0个 B.1个 C.2个 D.3个
9.已知点A(-1,0),点B(2,0),在y轴上存在点C,使三角形ABC的面积为6,则点C的坐标是( )
A.(0,4) B.(0,2) C.(0,2)或(0,-2) D.(0,4)或(0,-4)
10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2023次运动后,动点P的坐标是( )
A.(2023,0) B.(2023,1) C.(2023,2) D.(2024,0)
二、填空题(本大题共4小题,每小题3分,满分12分)
11.一张电影票的座位5排2号记为(5,2),则3排5号记为_______.
12.将点(0,1)向下平移2个单位长度后,所得点的坐标为________.
13.点P(a+5,a-2)在x轴上,则P点坐标为_______.
14.学完了“平面直角坐标系”后,李宇同学在笔记本上写了下列一些体会:
①如果一个点的横、纵坐标都为零,那么这个点是原点;
②如果一个点在x轴上,那么它一定不属于任何象限;
③纵轴上的点的横坐标均相等,且都等于零;
④纵坐标相同的点,分布在平行于y轴的某条直线上.
其中你认为正确的有_____(把正确的序号填在横线上).
三、解答题(本大题共9小题,满分58分)
15.(5分)如图,点A的位置为(2,6),小明从点A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从点A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格
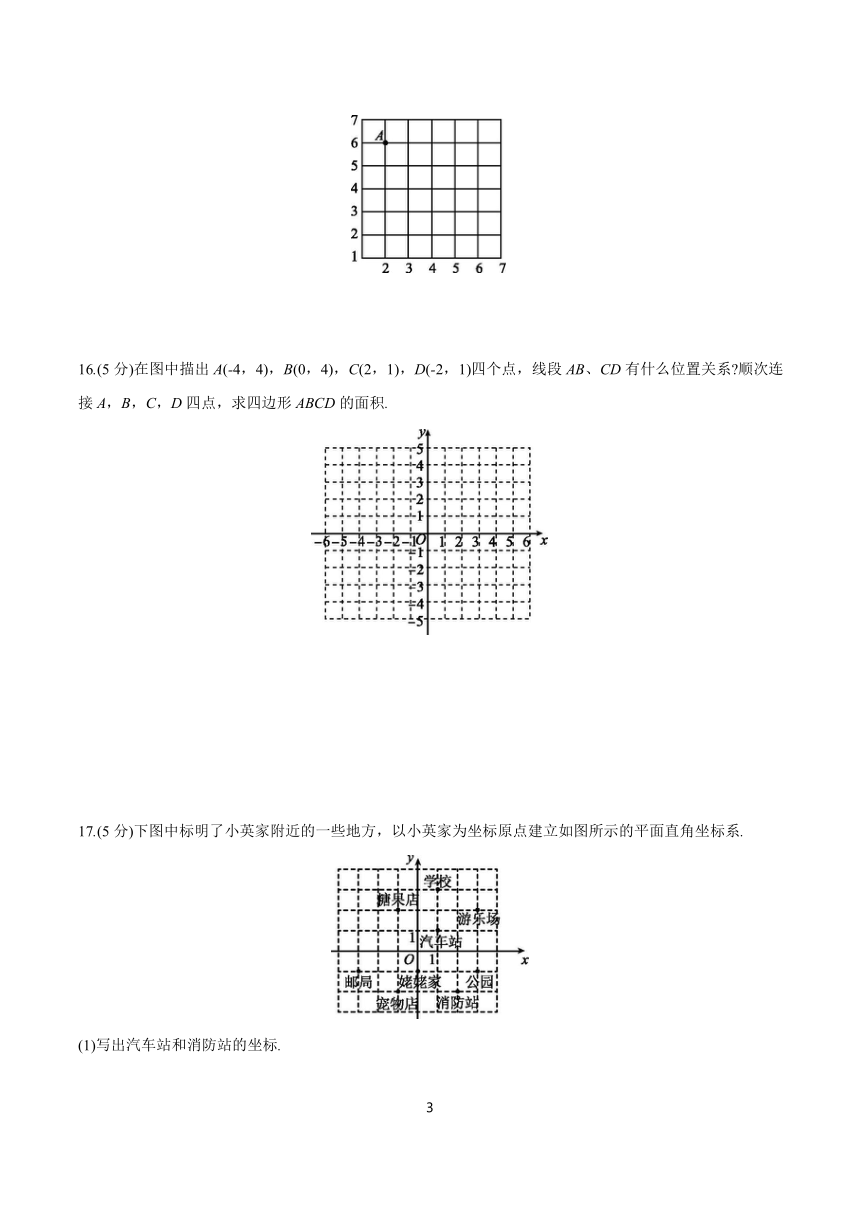
16.(5分)在图中描出A(-4,4),B(0,4),C(2,1),D(-2,1)四个点,线段AB、CD有什么位置关系 顺次连接A,B,C,D四点,求四边形ABCD的面积.
17.(5分)下图中标明了小英家附近的一些地方,以小英家为坐标原点建立如图所示的平面直角坐标系.
(1)写出汽车站和消防站的坐标.
(2)某星期日早晨,小英同学从家里出发,沿(3,2)→(3,-1)→(0,-1)→(-1,-2)→(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
18.(5分)如图,平面直角坐标系中,△ABC的顶点都在网格点上,平移△ABC,使点B与坐标原点O重合,请写出图中点A,B,C的坐标,并画出平移后的△A1OC1.
19.(6分)国庆期间,笑笑所在的学习小组组织了到方特梦幻王国的游园活动,笑笑和乐乐对着景区示意图(如图所示)讨论景点位置(图中小正方形边长代表100 m).
笑笑说:“西游传说坐标(300,300).”
乐乐说:“华夏五千年坐标(-100,-400).”
若他们二人所说的位置都正确.
(1)在图中建立适当的平面直角坐标系xOy.
(2)用坐标描述其他地点的位置.
20.(7分)在平面直角坐标系中:
(1)若点M(m-6,2m+3)到两坐标轴的距离相等,求点M的坐标;
(2)若点M(m-6,2m+3),点N(5,2),且MN∥y轴,求点M的坐标;
(3)若点M(a,b),点N(5,2),且MN∥x轴,MN=3,求点M的坐标.
21.(8分)对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P'为点P的“k属派生点”.例如:点P(1,4)的“2属派生点”为P'(1+2×4,2×1+4),即P'(9,6).
(1)点P(-2,3)的“2属派生点”P'的坐标为______.
(2)若点P的“4属派生点”P'的坐标为(2,-7),求点P的坐标.
(3)若点P在y轴的正半轴上,点P的“k属派生点”为P'点,且PP'=3OP,求k的值.
22.(8分)如图,已知点A(a,0)和B(0,b)满足(a-4)2+|b-6|=0,分别过点A,B作x轴,y轴的垂线交于点C,点P从原点出发,以每秒2个单位长度的速度沿着O→B→C→A→O的路线移动.
(1)写出A,B,C三点的坐标.
(2)当点P移动了6秒时,直接写出点P的坐标.
(3)连接(2)中B,P两点,将线段BP向下平移h个单位长度(h>0),得到B'P'.若B'P'将四边形OACB的分成面积相等的两部分,求h的值.
23.(9分)综合与实践
问题背景:
(1)已知三点A(1,2),B(3,2),C(1,-1),D(-3,-3).在平面直角坐标系中描出这几个点,并分别写出线段AB和CD的中点P1,P2的坐标.
探究发现:
(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为________.
拓展应用:
(3)利用上述规律解决下列问题:已知三点E(-1,2),F(3,1),G(1,4),第四个点H(x,y)与E,F,G三点中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.
参考答案
1.C 2.D 3.B 4.D 5.C 6.D 7.B 8.C 9.D
10.C 11.(3,5) 12.(0,-1) 13.(7,0) 14.①②③
15.【解析】如图,可知小明与小刚相距3个格.
16.【解析】画出图形,直接得到AB∥x轴,DC∥x轴,所以AB∥CD.S四边形ABCD=4×3=12.
17.【解析】(1)汽车站(1,1),消防站(2,-2).
(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
18.【解析】A(2,-1),B(4,3),C(1,2).
如图,△A1OC1为所求.
19.【解析】(1)如图所示.
(2)太空飞梭(0,0),秦岭历险(0,400),魔幻城堡(400,-200),南门(0,-500),丛林飞龙(-200,-100).
20.【解析】(1)∵点M(m-6,2m+3)到两坐标轴的距离相等,
∴|m-6|=|2m+3|,
当6-m=2m+3时,
解得m=1,m-6=-5,2m+3=5,
∴点M的坐标为(-5,5).
当6-m=-2m-3时,解得m=-9,m-6=-15,2m+3=2×(-9)+3=-15,
∴点M的坐标为(-15,-15).
综上所述,点M的坐标为(-5,5)或(-15,-15).
(2)∵MN∥y轴,
∴m-6=5,
解得m=11,m-6=11-6=5,2m+3=2×11+3=25,
∴点M的坐标(5,25).
(3)∵MN∥x轴,
∴b=2,
当点M在点N左侧时,a=5-3=2;
当点M在点N右侧时,a=5+3=8.
∴点M坐标为(2,2)或(8,2).
21.【解析】(1)由定义可知,-2+2×3=4,2×(-2)+3=-1,
∴P'的坐标为(4,-1),
故答案为(4,-1).
(2)设P(a,b),
∴2=a+4b,-7=4a+b,
∴a=-2,b=1,
∴P(-2,1).
(3)∵点P在y轴的正半轴上,
∴P点的横坐标为0,设P(0,b),b>0,
则点P的“k属派生点”P'点为(kb,b),
∴PP'=|kb|,PO=|b|.
∵线段PP'的长度为线段OP长度的3倍,
∴|kb|=3|b|,
∴k=±3.
22.【解析】(1)∵(a-4)2+|b-6|=0,
∴a-4=0且b-6=0,解得a=4,b=6,
∴点A,B的坐标分别为(4,0)和(0,6),
∴点C的坐标为(4,6).
(2)点P的坐标为(4,4).
(3)如图,将线段BP向下平移h个单位长度,
则BB'=h,CP'=2+h,B'O=6-h,P'A=6-2-h,
若B'P'将四边形OACB的分成面积相等的两部分,则BB'+CP'=B'O+P'A,
∴h+2+h=6-h+6-2-h,4h=8,
解得h=2,
即当h=2时,B'P'平分四边形OACB的面积.
23.【解析】(1)如图,A(1,2),B(3,2),C(1,-1),D(-3,-3).在平面直角坐标系中描出它们如图所示:
线段AB和CD的中点P1,P2的坐标分别为(2,2),(-1,-2).
(2)若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为.
故答案为.
(3)∵E(-1,2),F(3,1),G(1,4),
∴线段EF,FG,EG的中点分别为,,(0,3).
①当HG过EF的中点时,=1,=,
解得x=1,y=-1,故H(1,-1);
②当EH过FG的中点时,=2,=,
解得x=5,y=3,故H(5,3);
③当FH过EG的中点(0,3)时,=0,=3,
解得x=-3,y=5,故H(-3,5).
综上所述,点H的坐标为(1,-1),(5,3)或(-3,5).
2
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.平面直角坐标系中,和有序实数对一一对应的是( )
A.x轴上的点 B.y轴上的点
C.平面直角坐标系内的点 D.x轴和y轴上的点
2.点P(5,-3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.坐标为(x,x-1)的点一定不会在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点A(3,1),B(2,2),则“宝藏”点C的位置是( )
A.(1,0) B.(1,2) C.(2,1) D.(1,1)
5.若点P在第四象限,且到x轴的距离是2,到y轴的距离是4,则P点的坐标为( )
A.(2,4) B.(-4,2) C.(4,-2) D.(-2,4)
6.小李在平面直角坐标系中画了一张示意图,分别标出了学校、电影院、体育馆、超市的大致位置.如果张大妈从体育馆向南走150米,再向东走400米,再向南走250米,再向西走50米,最终到达的地点是( )
A.学校 B.电影院 C.体育馆 D.超市
7.在平面直角坐标系中,点A,B的坐标分别为(1,0),(3,2),连接AB,将线段AB平移后得到线段A'B',点A的对应点A'坐标为(2,1),则点B'坐标为( )
A.(4,2) B.(4,3) C.(6,2) D.(6,3)
8.下列语句,其中正确的有( )
①点(3,2)与(2,3)是同一个点;②点(0,-2)在x轴上;③点(0,0)是坐标原点;④点(-2,-6)在第三象限内.
A.0个 B.1个 C.2个 D.3个
9.已知点A(-1,0),点B(2,0),在y轴上存在点C,使三角形ABC的面积为6,则点C的坐标是( )
A.(0,4) B.(0,2) C.(0,2)或(0,-2) D.(0,4)或(0,-4)
10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2023次运动后,动点P的坐标是( )
A.(2023,0) B.(2023,1) C.(2023,2) D.(2024,0)
二、填空题(本大题共4小题,每小题3分,满分12分)
11.一张电影票的座位5排2号记为(5,2),则3排5号记为_______.
12.将点(0,1)向下平移2个单位长度后,所得点的坐标为________.
13.点P(a+5,a-2)在x轴上,则P点坐标为_______.
14.学完了“平面直角坐标系”后,李宇同学在笔记本上写了下列一些体会:
①如果一个点的横、纵坐标都为零,那么这个点是原点;
②如果一个点在x轴上,那么它一定不属于任何象限;
③纵轴上的点的横坐标均相等,且都等于零;
④纵坐标相同的点,分布在平行于y轴的某条直线上.
其中你认为正确的有_____(把正确的序号填在横线上).
三、解答题(本大题共9小题,满分58分)
15.(5分)如图,点A的位置为(2,6),小明从点A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从点A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格
16.(5分)在图中描出A(-4,4),B(0,4),C(2,1),D(-2,1)四个点,线段AB、CD有什么位置关系 顺次连接A,B,C,D四点,求四边形ABCD的面积.
17.(5分)下图中标明了小英家附近的一些地方,以小英家为坐标原点建立如图所示的平面直角坐标系.
(1)写出汽车站和消防站的坐标.
(2)某星期日早晨,小英同学从家里出发,沿(3,2)→(3,-1)→(0,-1)→(-1,-2)→(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
18.(5分)如图,平面直角坐标系中,△ABC的顶点都在网格点上,平移△ABC,使点B与坐标原点O重合,请写出图中点A,B,C的坐标,并画出平移后的△A1OC1.
19.(6分)国庆期间,笑笑所在的学习小组组织了到方特梦幻王国的游园活动,笑笑和乐乐对着景区示意图(如图所示)讨论景点位置(图中小正方形边长代表100 m).
笑笑说:“西游传说坐标(300,300).”
乐乐说:“华夏五千年坐标(-100,-400).”
若他们二人所说的位置都正确.
(1)在图中建立适当的平面直角坐标系xOy.
(2)用坐标描述其他地点的位置.
20.(7分)在平面直角坐标系中:
(1)若点M(m-6,2m+3)到两坐标轴的距离相等,求点M的坐标;
(2)若点M(m-6,2m+3),点N(5,2),且MN∥y轴,求点M的坐标;
(3)若点M(a,b),点N(5,2),且MN∥x轴,MN=3,求点M的坐标.
21.(8分)对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P'为点P的“k属派生点”.例如:点P(1,4)的“2属派生点”为P'(1+2×4,2×1+4),即P'(9,6).
(1)点P(-2,3)的“2属派生点”P'的坐标为______.
(2)若点P的“4属派生点”P'的坐标为(2,-7),求点P的坐标.
(3)若点P在y轴的正半轴上,点P的“k属派生点”为P'点,且PP'=3OP,求k的值.
22.(8分)如图,已知点A(a,0)和B(0,b)满足(a-4)2+|b-6|=0,分别过点A,B作x轴,y轴的垂线交于点C,点P从原点出发,以每秒2个单位长度的速度沿着O→B→C→A→O的路线移动.
(1)写出A,B,C三点的坐标.
(2)当点P移动了6秒时,直接写出点P的坐标.
(3)连接(2)中B,P两点,将线段BP向下平移h个单位长度(h>0),得到B'P'.若B'P'将四边形OACB的分成面积相等的两部分,求h的值.
23.(9分)综合与实践
问题背景:
(1)已知三点A(1,2),B(3,2),C(1,-1),D(-3,-3).在平面直角坐标系中描出这几个点,并分别写出线段AB和CD的中点P1,P2的坐标.
探究发现:
(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为________.
拓展应用:
(3)利用上述规律解决下列问题:已知三点E(-1,2),F(3,1),G(1,4),第四个点H(x,y)与E,F,G三点中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.
参考答案
1.C 2.D 3.B 4.D 5.C 6.D 7.B 8.C 9.D
10.C 11.(3,5) 12.(0,-1) 13.(7,0) 14.①②③
15.【解析】如图,可知小明与小刚相距3个格.
16.【解析】画出图形,直接得到AB∥x轴,DC∥x轴,所以AB∥CD.S四边形ABCD=4×3=12.
17.【解析】(1)汽车站(1,1),消防站(2,-2).
(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
18.【解析】A(2,-1),B(4,3),C(1,2).
如图,△A1OC1为所求.
19.【解析】(1)如图所示.
(2)太空飞梭(0,0),秦岭历险(0,400),魔幻城堡(400,-200),南门(0,-500),丛林飞龙(-200,-100).
20.【解析】(1)∵点M(m-6,2m+3)到两坐标轴的距离相等,
∴|m-6|=|2m+3|,
当6-m=2m+3时,
解得m=1,m-6=-5,2m+3=5,
∴点M的坐标为(-5,5).
当6-m=-2m-3时,解得m=-9,m-6=-15,2m+3=2×(-9)+3=-15,
∴点M的坐标为(-15,-15).
综上所述,点M的坐标为(-5,5)或(-15,-15).
(2)∵MN∥y轴,
∴m-6=5,
解得m=11,m-6=11-6=5,2m+3=2×11+3=25,
∴点M的坐标(5,25).
(3)∵MN∥x轴,
∴b=2,
当点M在点N左侧时,a=5-3=2;
当点M在点N右侧时,a=5+3=8.
∴点M坐标为(2,2)或(8,2).
21.【解析】(1)由定义可知,-2+2×3=4,2×(-2)+3=-1,
∴P'的坐标为(4,-1),
故答案为(4,-1).
(2)设P(a,b),
∴2=a+4b,-7=4a+b,
∴a=-2,b=1,
∴P(-2,1).
(3)∵点P在y轴的正半轴上,
∴P点的横坐标为0,设P(0,b),b>0,
则点P的“k属派生点”P'点为(kb,b),
∴PP'=|kb|,PO=|b|.
∵线段PP'的长度为线段OP长度的3倍,
∴|kb|=3|b|,
∴k=±3.
22.【解析】(1)∵(a-4)2+|b-6|=0,
∴a-4=0且b-6=0,解得a=4,b=6,
∴点A,B的坐标分别为(4,0)和(0,6),
∴点C的坐标为(4,6).
(2)点P的坐标为(4,4).
(3)如图,将线段BP向下平移h个单位长度,
则BB'=h,CP'=2+h,B'O=6-h,P'A=6-2-h,
若B'P'将四边形OACB的分成面积相等的两部分,则BB'+CP'=B'O+P'A,
∴h+2+h=6-h+6-2-h,4h=8,
解得h=2,
即当h=2时,B'P'平分四边形OACB的面积.
23.【解析】(1)如图,A(1,2),B(3,2),C(1,-1),D(-3,-3).在平面直角坐标系中描出它们如图所示:
线段AB和CD的中点P1,P2的坐标分别为(2,2),(-1,-2).
(2)若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为.
故答案为.
(3)∵E(-1,2),F(3,1),G(1,4),
∴线段EF,FG,EG的中点分别为,,(0,3).
①当HG过EF的中点时,=1,=,
解得x=1,y=-1,故H(1,-1);
②当EH过FG的中点时,=2,=,
解得x=5,y=3,故H(5,3);
③当FH过EG的中点(0,3)时,=0,=3,
解得x=-3,y=5,故H(-3,5).
综上所述,点H的坐标为(1,-1),(5,3)或(-3,5).
2
