第8章 二元一次方程组 分层作业 (含答案)2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 第8章 二元一次方程组 分层作业 (含答案)2023-2024学年初中数学人教版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 60.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 00:00:00 | ||
图片预览




文档简介
第八章 二元一次方程组 自我评估
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10个小题,每小题3分,满分30分)
1.下列四个方程中,是二元一次方程的是( )
A.x-3=0 B.2x-z=5 C.3xy-5=8 D.+y=
2.用加减法解方程组下列解法不正确的是( )
A.①×2-②×(-3),消去y B.①×2-②×3,消去y
C.①×(-3)+②×2,消去x D.①×3-②×2,消去x
3.二元一次方程组的解是( )
A. B. C. D.
4.已知是方程3x-y=5的一个解,则a的值是( )
A.5 B.1 C.-5 D.-1
5.已知方程组的解为则○, 分别为( )
A.-6,-1 B.-6,1 C.6,1 D.6,-1
6.若-3=12是二元一次方程,则m,n的值分别为( )
A.0,1 B.2,1 C.1,0 D.2,3
7.已知关于x,y的方程组甲看错了a得到的解为乙看错了b得到的解为他们分别把a,b错看成的值为( )
A.a=5,b=-1 B.a=5,b= C.a=-1,b= D.a=-1,b=-1
8.为了美化校园,学校计划购买甲、乙两种花木共200棵进行绿化,其中甲种花木每棵80元,乙种花木每棵100元,若购买甲、乙两种花木共花费17600元,问学校购买甲、乙两种花木各多少棵 设购买甲种花木x棵,乙种花木y棵,根据题意列出的方程组正确的是( )
A. B.
C. D.
9.已知关于x,y的方程组和有相同的解,那么的算术平方根是( )
A.0 B.± C. D.2
10.已知运输360吨化肥,装载了6节火车车厢和15辆汽车;运输440吨化肥,装载了8节火车车厢和10辆汽车.则10节火车车厢和20辆汽车能运输的化肥吨数为( )
A.580 B.720 C.860 D.1100
二、填空题(本大题共4小题,每小题3分,满分12分)
11.已知方程5x+4y-3=0,改写成用含x的式子表示y的形式为y=____.
12.若a-3b=2,3a-b=6,则b-a的值为____.
13.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是第___象限.
14.一名学生问老师:“你今年多大了 ”老师风趣地说:“我像你这样大的时候,你才2岁;你到我这么大时,我已经38岁了.”则今年老师的岁数是____.
三、解答题(本大题共9小题,满分58分)
15.(5分)解方程组时,甲、乙两位同学的解题过程如下.
甲:由①-②,得3x=3.
乙:由②得3x+(x-3y)=5③,
把①代入③,得3x+8=5.
(1)反思:你发现___的解题过程有错误(填“甲”或“乙”),从甲、乙两位同学的解题过程,可以得出解二元一次方程组的基本思想是______.
(2)请选择一种你喜欢的方法解上述方程组.
16.(5分)已知关于x,y的二元一次方程y=kx+b(k,b为常数)的正整数解如表所示:
y=kx+b x 1 2 3
y 5 3 1
求k和b的值.
17.(5分)对于有理数,规定新运算:x※y=ax+by+xy,其中a,b是常数,等式右边是通常的加法和乘法运算,已知2※1=9,(-3)※3=3,求a,b的值.
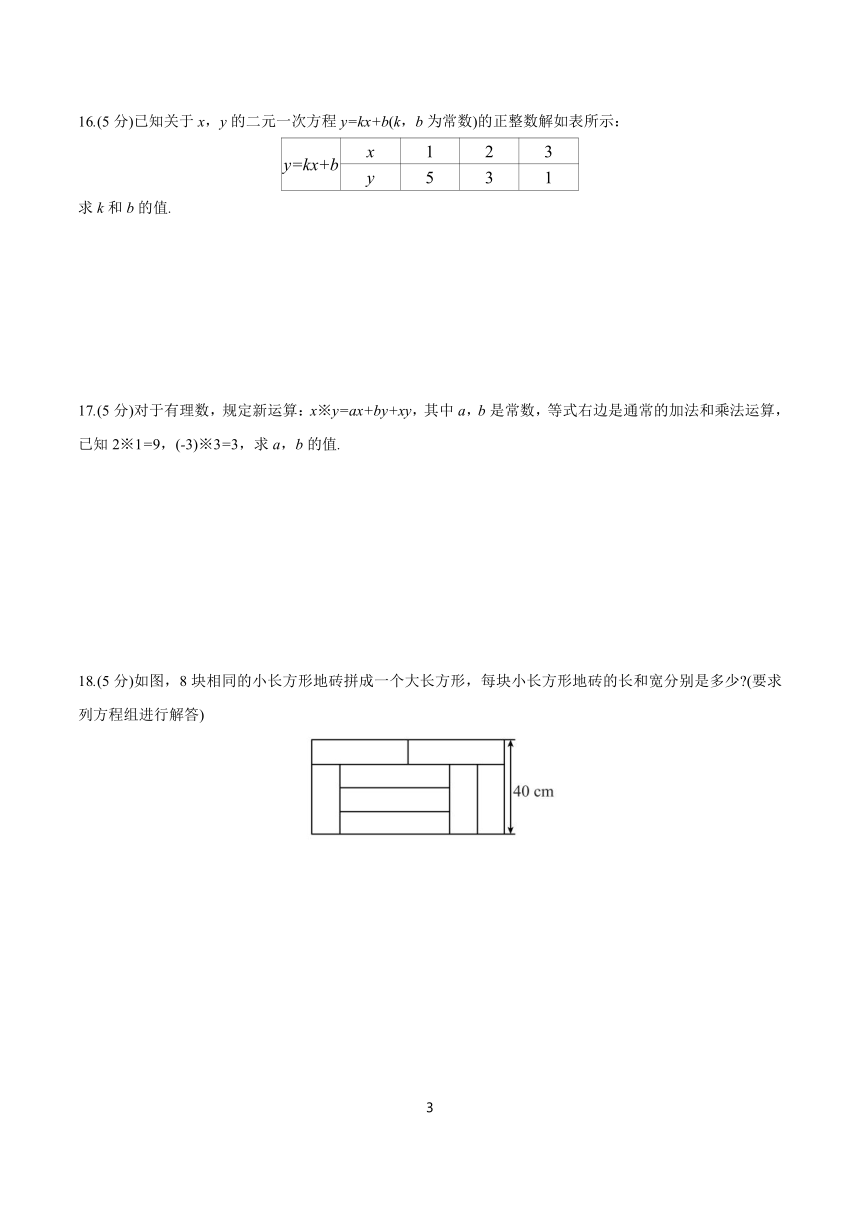
18.(5分)如图,8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (要求列方程组进行解答)
19.(6分)解方程组时,甲因看错了a的符号,从而求得解为乙因看漏了c,从而求得解为试求a,b,c的值.
20.(6分)某旅馆的客房有三人间和两人间两种,三人间每人每天25元,两人间每人每天35元,一个21人的旅游团到该旅馆住宿,租住了若干间客房,且每间客房正好住满,一天共花去住宿费645元,则两种客房各租住了多少间
21.(8分)[阅读理解]在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化繁为简.
(1)解方程组 解:把②代入①,得x+2×1=3, 解得x=1. 把x=1代入②得y=0, 所以方程组的解为
(2)已知求x+y+z的值. 解:①+②,得10x+10y+10z=40③, ③÷10,得x+y+z=4.
[类比迁移]
(1)求方程组的解.
(2)若求x+y+z的值.
[实际应用]打折前,买36件A商品,12件B商品共用了960元.打折后,买45件A商品,15件B商品共用了1100元,比打折前少花了多少钱
22.(8分)某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是200 cm×40 cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图甲所示(单位:cm).
(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将25张标准板材用裁法一裁剪,将5张标准板材用裁法二裁剪,再将得到的A型与B型板材分别做侧面和底面,刚好可以做成图乙的竖式与横式两种无盖礼品盒,则可以做竖式与横式两种无盖礼品盒各多少个
23.(10分)为了进一步发展中医药,现欲将某中药材生产基地的一批中药材运往外地,若用2辆A型车和1辆B型车载满中药材一次可运走10吨;若用1辆A型车和2辆B型车载满中药材一次可运走11吨.现有中药材31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满中药材.根据以上信息,解答问题:
(1)1辆A型车和1辆B型车都载满中药材一次可分别运送多少吨
(2)请你帮该物流公司设计租车方案;
(3)若1辆A型车需租金100元/次,1辆B型车需租金120元/次,请选出费用最少的租车方案,并求出最少租车费.
参考答案
1.B 2.A 3.B 4.B 5.C 6.B 7.A 8.A 9.C
10.A
11.
12.-2
13.四
14.26
15.【解析】(1)甲 消元思想
(2)②-①,得3x=-3,解得x=-1.
将x=-1代入①,得-1-3y=8,解得y=-3,
所以该方程组的解为(方法不唯一)
16.【解析】把x=1,y=5;x=2,y=3代入y=kx+b,得
解得
则k和b的值分别为-2和7.
17.【解析】依题意得
解得
18.【解析】设每块小长方形地砖的长为x cm,宽为y cm.由题意得解得
答:每块小长方形地砖的长是30 cm,宽是10 cm.
19.【解析】∵甲看错了a的符号,
∴把x=3,y=2代入x+cy=4,
得c=.
∵甲看错了a的符号,
∴-3a+2b=6.
∵乙看漏了c,
∴把x=6,y=-2代入ax+by=6,
得6a-2b=6,
得
解得a=4,b=9.
20.【解析】设租住三人间x间,两人间y间.
根据题意得
解得
答:租住三人间3间,两人间6间.
21.【解析】[类比迁移](1)把②代入①,
得3×2+4=2a,解得a=5.
把a=5代入②,得b=3,
∴方程组的解为
(2)①-②得4x+4y+4z=4,
∴x+y+z=1.
[实际应用]设打折前A商品每件x元,B商品每件y元,
根据题意得36x+12y=960,
等式两边同时乘,得45x+15y=1200,
1200-1100=100(元).
答:比打折前少花了100元.
22.【解析】(1)依题意得
解得
答:图中的a与b的值分别为50与40.
(2)设可以做竖式无盖礼品盒x个,横式无盖礼品盒y个.
依题意得
解得
答:可以做竖式无盖礼品盒8个,横式无盖礼品盒16个.
23.【解析】(1)设1辆A型车载满中药材一次可运送x吨,1辆B型车载满中药材一次可运送y吨.
依题意得
解得
答:1辆A型车载满中药材一次可运送3吨,1辆B型车载满中药材一次可运送4吨.
(2)依题意得3a+4b=31,
∴a=.
又∵a,b均为正整数,
∴或或
∴该物流公司共有3种租车方案,
方案1:租用9辆A型车,1辆B型车;
方案2:租用5辆A型车,4辆B型车;
方案3:租用1辆A型车,7辆B型车.
(3)选择方案1所需的租车费用为100×9+120×1=900+120=1020(元);
选择方案2所需的租车费用为100×5+120×4=500+480=980(元);
选择方案3所需的租车费用为100×1+120×7=100+840=940(元).
∵1020>980>940,
∴费用最少的租车方案为租用1辆A型车,7辆B型车,最少租车费为940元.
2
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10个小题,每小题3分,满分30分)
1.下列四个方程中,是二元一次方程的是( )
A.x-3=0 B.2x-z=5 C.3xy-5=8 D.+y=
2.用加减法解方程组下列解法不正确的是( )
A.①×2-②×(-3),消去y B.①×2-②×3,消去y
C.①×(-3)+②×2,消去x D.①×3-②×2,消去x
3.二元一次方程组的解是( )
A. B. C. D.
4.已知是方程3x-y=5的一个解,则a的值是( )
A.5 B.1 C.-5 D.-1
5.已知方程组的解为则○, 分别为( )
A.-6,-1 B.-6,1 C.6,1 D.6,-1
6.若-3=12是二元一次方程,则m,n的值分别为( )
A.0,1 B.2,1 C.1,0 D.2,3
7.已知关于x,y的方程组甲看错了a得到的解为乙看错了b得到的解为他们分别把a,b错看成的值为( )
A.a=5,b=-1 B.a=5,b= C.a=-1,b= D.a=-1,b=-1
8.为了美化校园,学校计划购买甲、乙两种花木共200棵进行绿化,其中甲种花木每棵80元,乙种花木每棵100元,若购买甲、乙两种花木共花费17600元,问学校购买甲、乙两种花木各多少棵 设购买甲种花木x棵,乙种花木y棵,根据题意列出的方程组正确的是( )
A. B.
C. D.
9.已知关于x,y的方程组和有相同的解,那么的算术平方根是( )
A.0 B.± C. D.2
10.已知运输360吨化肥,装载了6节火车车厢和15辆汽车;运输440吨化肥,装载了8节火车车厢和10辆汽车.则10节火车车厢和20辆汽车能运输的化肥吨数为( )
A.580 B.720 C.860 D.1100
二、填空题(本大题共4小题,每小题3分,满分12分)
11.已知方程5x+4y-3=0,改写成用含x的式子表示y的形式为y=____.
12.若a-3b=2,3a-b=6,则b-a的值为____.
13.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是第___象限.
14.一名学生问老师:“你今年多大了 ”老师风趣地说:“我像你这样大的时候,你才2岁;你到我这么大时,我已经38岁了.”则今年老师的岁数是____.
三、解答题(本大题共9小题,满分58分)
15.(5分)解方程组时,甲、乙两位同学的解题过程如下.
甲:由①-②,得3x=3.
乙:由②得3x+(x-3y)=5③,
把①代入③,得3x+8=5.
(1)反思:你发现___的解题过程有错误(填“甲”或“乙”),从甲、乙两位同学的解题过程,可以得出解二元一次方程组的基本思想是______.
(2)请选择一种你喜欢的方法解上述方程组.
16.(5分)已知关于x,y的二元一次方程y=kx+b(k,b为常数)的正整数解如表所示:
y=kx+b x 1 2 3
y 5 3 1
求k和b的值.
17.(5分)对于有理数,规定新运算:x※y=ax+by+xy,其中a,b是常数,等式右边是通常的加法和乘法运算,已知2※1=9,(-3)※3=3,求a,b的值.
18.(5分)如图,8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (要求列方程组进行解答)
19.(6分)解方程组时,甲因看错了a的符号,从而求得解为乙因看漏了c,从而求得解为试求a,b,c的值.
20.(6分)某旅馆的客房有三人间和两人间两种,三人间每人每天25元,两人间每人每天35元,一个21人的旅游团到该旅馆住宿,租住了若干间客房,且每间客房正好住满,一天共花去住宿费645元,则两种客房各租住了多少间
21.(8分)[阅读理解]在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化繁为简.
(1)解方程组 解:把②代入①,得x+2×1=3, 解得x=1. 把x=1代入②得y=0, 所以方程组的解为
(2)已知求x+y+z的值. 解:①+②,得10x+10y+10z=40③, ③÷10,得x+y+z=4.
[类比迁移]
(1)求方程组的解.
(2)若求x+y+z的值.
[实际应用]打折前,买36件A商品,12件B商品共用了960元.打折后,买45件A商品,15件B商品共用了1100元,比打折前少花了多少钱
22.(8分)某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是200 cm×40 cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图甲所示(单位:cm).
(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将25张标准板材用裁法一裁剪,将5张标准板材用裁法二裁剪,再将得到的A型与B型板材分别做侧面和底面,刚好可以做成图乙的竖式与横式两种无盖礼品盒,则可以做竖式与横式两种无盖礼品盒各多少个
23.(10分)为了进一步发展中医药,现欲将某中药材生产基地的一批中药材运往外地,若用2辆A型车和1辆B型车载满中药材一次可运走10吨;若用1辆A型车和2辆B型车载满中药材一次可运走11吨.现有中药材31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满中药材.根据以上信息,解答问题:
(1)1辆A型车和1辆B型车都载满中药材一次可分别运送多少吨
(2)请你帮该物流公司设计租车方案;
(3)若1辆A型车需租金100元/次,1辆B型车需租金120元/次,请选出费用最少的租车方案,并求出最少租车费.
参考答案
1.B 2.A 3.B 4.B 5.C 6.B 7.A 8.A 9.C
10.A
11.
12.-2
13.四
14.26
15.【解析】(1)甲 消元思想
(2)②-①,得3x=-3,解得x=-1.
将x=-1代入①,得-1-3y=8,解得y=-3,
所以该方程组的解为(方法不唯一)
16.【解析】把x=1,y=5;x=2,y=3代入y=kx+b,得
解得
则k和b的值分别为-2和7.
17.【解析】依题意得
解得
18.【解析】设每块小长方形地砖的长为x cm,宽为y cm.由题意得解得
答:每块小长方形地砖的长是30 cm,宽是10 cm.
19.【解析】∵甲看错了a的符号,
∴把x=3,y=2代入x+cy=4,
得c=.
∵甲看错了a的符号,
∴-3a+2b=6.
∵乙看漏了c,
∴把x=6,y=-2代入ax+by=6,
得6a-2b=6,
得
解得a=4,b=9.
20.【解析】设租住三人间x间,两人间y间.
根据题意得
解得
答:租住三人间3间,两人间6间.
21.【解析】[类比迁移](1)把②代入①,
得3×2+4=2a,解得a=5.
把a=5代入②,得b=3,
∴方程组的解为
(2)①-②得4x+4y+4z=4,
∴x+y+z=1.
[实际应用]设打折前A商品每件x元,B商品每件y元,
根据题意得36x+12y=960,
等式两边同时乘,得45x+15y=1200,
1200-1100=100(元).
答:比打折前少花了100元.
22.【解析】(1)依题意得
解得
答:图中的a与b的值分别为50与40.
(2)设可以做竖式无盖礼品盒x个,横式无盖礼品盒y个.
依题意得
解得
答:可以做竖式无盖礼品盒8个,横式无盖礼品盒16个.
23.【解析】(1)设1辆A型车载满中药材一次可运送x吨,1辆B型车载满中药材一次可运送y吨.
依题意得
解得
答:1辆A型车载满中药材一次可运送3吨,1辆B型车载满中药材一次可运送4吨.
(2)依题意得3a+4b=31,
∴a=.
又∵a,b均为正整数,
∴或或
∴该物流公司共有3种租车方案,
方案1:租用9辆A型车,1辆B型车;
方案2:租用5辆A型车,4辆B型车;
方案3:租用1辆A型车,7辆B型车.
(3)选择方案1所需的租车费用为100×9+120×1=900+120=1020(元);
选择方案2所需的租车费用为100×5+120×4=500+480=980(元);
选择方案3所需的租车费用为100×1+120×7=100+840=940(元).
∵1020>980>940,
∴费用最少的租车方案为租用1辆A型车,7辆B型车,最少租车费为940元.
2
