第10章 数据的收集、整理与描述 分层作业 (含答案)2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 第10章 数据的收集、整理与描述 分层作业 (含答案)2023-2024学年初中数学人教版七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 569.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 18:16:47 | ||
图片预览



文档简介
第十章 数据的收集、整理与描述 自我评估
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.下列调查中,最适合采用抽样调查的是( )
A.调查一批灯泡的质量
B.调查某校初一一班同学的视力
C.为保证某种新研发的大型客机试飞成功,对其零部件进行检查
D.对乘坐某班次飞机的乘客进行安检
2.下列统计图中,最宜反映气温变化的是( )
A.折线统计图 B.条形统计图 C.扇形统计图 D.频数分布直方图
3.为了解七年级4000名学生参加数学测试成绩的情况,从中随机抽取200名学生的数学成绩进行分析.下列说法正确的是( )
A.样本容量是200名 B.每名学生是个体
C.200名学生的数学成绩是总体的一个样本 D.4000名学生是总体
4.某公司今年7月1日~5日每天用水量变化情况如图所示,若设这5天的日最高用水量为a立方米,日最低用水量为b立方米,则a-b的值为( )
A.4 B.6 C.8 D.10
5.为了解游客在云台山、神农山和青天河这三个风景区旅游的满意率,数学小组的同学商议了几个收集数据的方案.方案一:在多家旅游公司调查300名导游.方案二:在云台山景区调查300名游客.方案三:在神农山景区调查300名游客.方案四:在三个景区各调查100名游客.其中最合理的方案是( )
A.方案一 B.方案二 C.方案三 D.方案四
6.春节前夕,学校向2000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹.B类:少放烟花爆竹.C类:使用电子鞭炮.D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,估计全校“使用电子鞭炮”的学生有( )
A.200名 B.400名 C.600名 D.750名
7.李老师对本班60名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别 A型 B型 O型 AB型
百分比 f 35% 15% 10%
A.6 B.9 C.21 D.24
8.为了解七年级学生的体能情况,抽取了某校该年级的部分学生进行一分钟跳绳测试,将所得数据整理后,画成如图所示的统计图,从左到右前三个小组所占的百分比分别为10%,30%,40%,从左至右第一小组若有5人,则第四小组的人数是( )
A.8 B.9 C.10 D.15
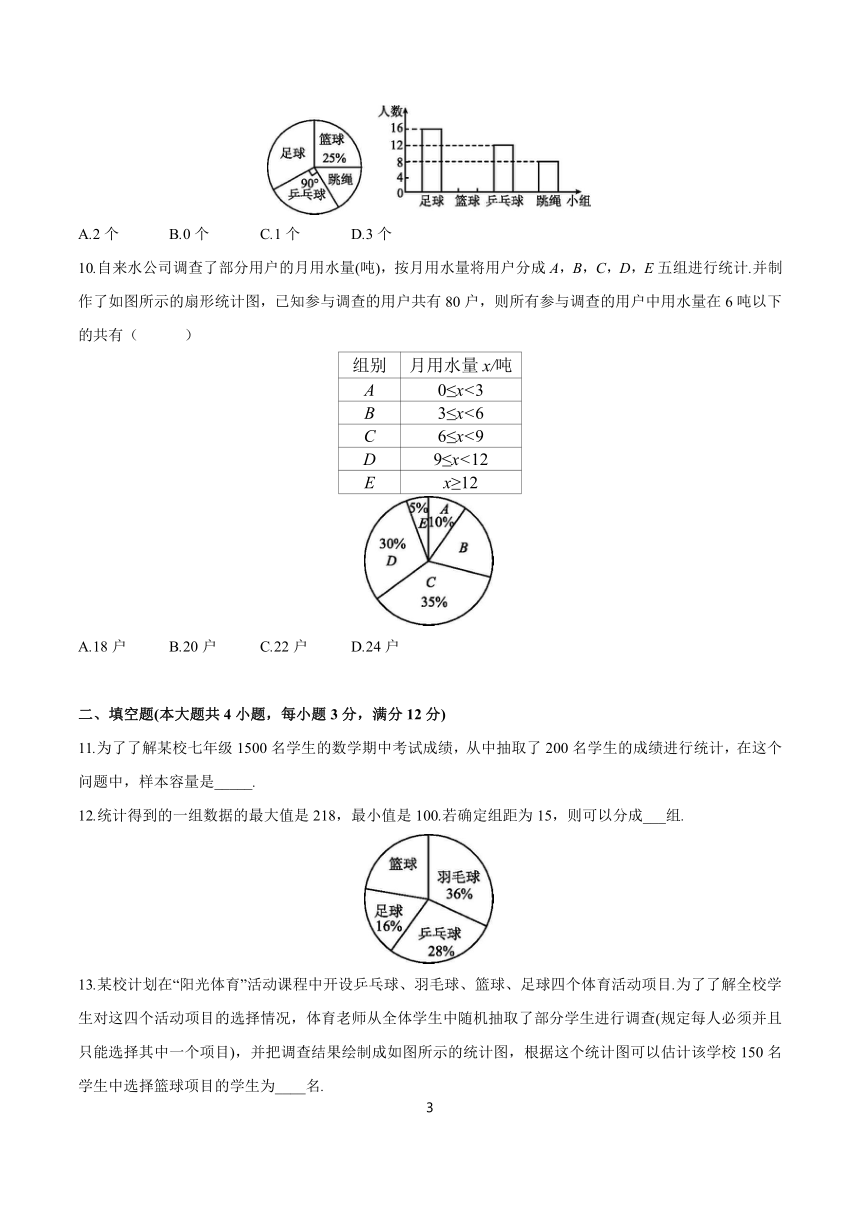
9.为加强锻炼增强体魄,我校初三(1)班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与各活动小组人数分布情况的扇形图和条形图如图所示,有下列说法:
①该班共有50名学生;
②篮球小组有16人;
③跳绳小组人数所占扇形圆心角为57.6°;
④足球小组人数所占扇形圆心角为120°.
这四种说法中正确的有( )
A.2个 B.0个 C.1个 D.3个
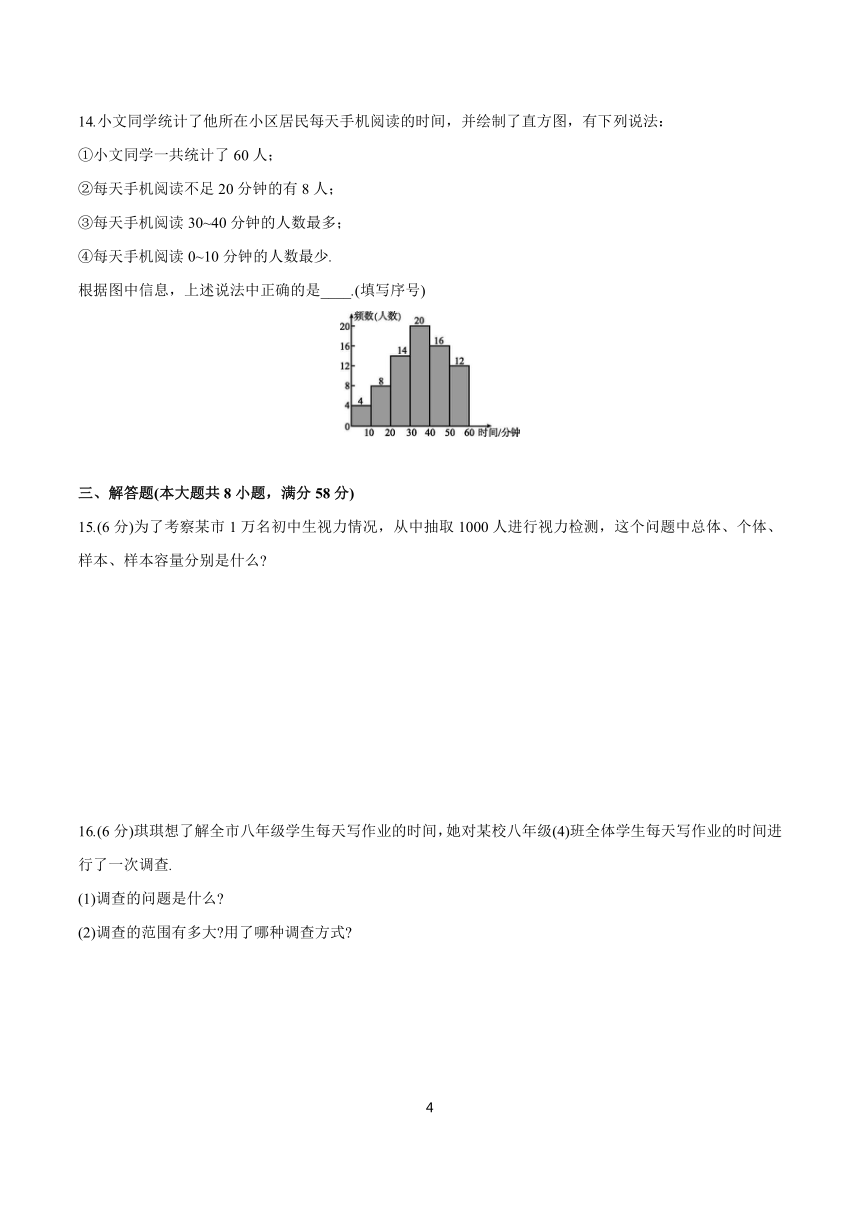
10.自来水公司调查了部分用户的月用水量(吨),按月用水量将用户分成A,B,C,D,E五组进行统计.并制作了如图所示的扇形统计图,已知参与调查的用户共有80户,则所有参与调查的用户中用水量在6吨以下的共有( )
组别 月用水量x/吨
A 0≤x<3
B 3≤x<6
C 6≤x<9
D 9≤x<12
E x≥12
A.18户 B.20户 C.22户 D.24户
二、填空题(本大题共4小题,每小题3分,满分12分)
11.为了了解某校七年级1500名学生的数学期中考试成绩,从中抽取了200名学生的成绩进行统计,在这个问题中,样本容量是_____.
12.统计得到的一组数据的最大值是218,最小值是100.若确定组距为15,则可以分成___组.
13.某校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目.为了了解全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中一个项目),并把调查结果绘制成如图所示的统计图,根据这个统计图可以估计该学校150名学生中选择篮球项目的学生为____名.
14.小文同学统计了他所在小区居民每天手机阅读的时间,并绘制了直方图,有下列说法:
①小文同学一共统计了60人;
②每天手机阅读不足20分钟的有8人;
③每天手机阅读30~40分钟的人数最多;
④每天手机阅读0~10分钟的人数最少.
根据图中信息,上述说法中正确的是____.(填写序号)
三、解答题(本大题共8小题,满分58分)
15.(6分)为了考察某市1万名初中生视力情况,从中抽取1000人进行视力检测,这个问题中总体、个体、样本、样本容量分别是什么
16.(6分)琪琪想了解全市八年级学生每天写作业的时间,她对某校八年级(4)班全体学生每天写作业的时间进行了一次调查.
(1)调查的问题是什么
(2)调查的范围有多大 用了哪种调查方式
17.(6分)为了考察4名篮球运动员投篮的命中率,让每名运动员投篮10次.
(1)你认为需要获取哪些数据 如何去获取这些数据
(2)记录员记下这4名篮球运动员投篮命中次数如下:
甲:正;乙:正;丙:正;丁:正正.
请将数据整理后填写下表.
篮球运动员 甲 乙 丙 丁
命中次数 ___ ___ ___ ___
命中率(%) ___ ___ ___ ___
18.(7分)观察如图所示的扇形统计图,然后解答问题.
(1)已知西红柿的种植面积是4.2公顷,三种蔬菜种植的总面积是____公顷.
(2)黄瓜的种植面积是___公顷.
(3)求茄子的种植面积是西红柿种植面积的百分之几.
19.(7分)网瘾低龄化问题已引起社会各界的高度关注,有关部门在全国范围内对12~35岁的网瘾人群进行简单随机抽样调查并得到如图所示的统计图,其中30~35岁的网瘾人数占样本人数的20%.
(1)请把图中缺失的数据、图形补充完整.
(2)若12~35岁的网瘾人数约为4000,请你根据图中数据估计网瘾人群中12~17岁的网瘾人数.
20.(8分)某校的20年校庆举办了四个项目的比赛,现分别以A,B,C,D表示它们.要求每位同学必须参加且限报一项.以七(1)班为样本进行统计,并将统计结果绘制成两幅统计图,其中参加A项目的人数比参加C与D项目人数的总和多1人,参加D项目的人数比参加A项目的人数少11人.请你结合图中所给出的信息解答下列问题:
(1)求出全班总人数;
(2)求出扇形统计图中参加D项目的学生所在的扇形圆心角的度数.
21.(8分)某校八年级共有8个班,241名同学,书法老师为了解该校八年级学生选修书法的意向,请小红、小亮、小军三位同学分别进行抽样调查.三位同学调查结果反馈如下:
(1)小红、小亮和小军三人中,你认为哪位同学的调查结果较好地反映了该校八年级同学选修书法的意向,并说出理由.
(2)估计八年级有意向选修书法的同学的人数.
22.(10分)“青年大学习”是共青团中央为组织引导广大青少年,深入学习贯彻习近平新时代中国特色社会主义思想和党的二十大精神的学习平台.我区某中学为了解学生的“青年大学习”的学习情况,组织了“青年大学习”知识竞赛,从中抽取了部分学生成绩进行统计(成绩均为整数,满分100分),按照成绩分成A,B,C,D,E五个小组,并绘制成不完整的统计表和统计图.
组别 分数段/分 频数/人数
A 50.5~60.5 a
B 60.5~70.5 40
C 70.5~80.5 c
D 80.5~90.5 70
E 90.5~100.5 24
合计 b
请结合上述信息完成下列问题:
(1)b=____,a=____;
(2)在扇形统计图中,D小组对应的圆心角的度数是____°;
(3)c=____,并补全频数分布直方图;
(4)若全校有2000名学生,成绩在80分以上(不含80分)为优秀,根据抽样调查结果,请估计该校学生成绩为优秀的人数.
参考答案
1.A 2.A 3.C 4.C 5.D 6.B 7.D 8.C 9.C
10.D 11.200 12.8 13.30 14.③④
15.【解析】总体:某市1万名初中生视力情况;
个体:每个初中生的视力情况;
样本:抽取的1000初中生的视力情况;
样本容量:1000.
16.【解析】(1)调查的问题是全市八年级学生每天写作业的时间.
(2)调查的范围是某校八年级(4)班全体学生,用了抽样调查方式.
17.【解析】(1)需要获取每位运动员投篮10次命中的次数,
可以让4名篮球运动员在相同的条件下进行投篮,记录每位运动员投篮10次命中的次数.
(2)将数据整理后填写表格如下.
篮球运动员 甲 乙 丙 丁
命中次数 9 6 8 10
命中率(%) 90% 60% 80% 100%
18.【解析】(1)三种蔬菜种植的总面积是4.2÷56%=7.5(公顷).
故答案为7.5.
(2)黄瓜的种植面积是7.5×30%=2.25(公顷).
故答案为2.25.
(3)茄子的种植面积是西红柿种植面积的×100%=25%.
19.【解析】(1)∵被调查的总人数为480÷20%=2400,
∴12~17岁的网瘾人数为2400-600-576-480=744(人),
补全图形如下:
(2)744÷2400×100%=31%,
4000×31%=1240(人),
∴若12~35岁的网瘾人数约为4000,则根据图中数据估计网瘾人群中12~17岁的网瘾人数是1240.
20.【解析】(1)全班的总人数为25÷50%=50.
答:全班的人数为50.
(2)设参加D项目的人数为x,C项目的人数为y,则A项目的人数为(x+11).
依题意得解得
所以参加D项目的人数为2,
所以参加D项目的学生所在的扇形圆心角的度数为×360°=14.4°.
答:在扇形统计图中参加D项目的学生所在的扇形圆心角的度数为14.4°.
21.【解析】(1)小军的数据较好地反映了该校八年级同学选修书法的意向.
理由如下:
小红仅调查了一个班的同学,样本不具有随机性;
小亮只调查了8位语文课代表,样本容量过少,不具有代表性;
小军的调查样本容量适中,且能够代表八年级的同学的选择意向.
(2)根据小军的调查结果,有意向选择书法的比例约为=,
故据此估计八年级有意向选修书法的同学人数为241×=60.25≈60.
22.【解析】(1)b=40÷20%=200,a=200×8%=16.
故答案为200;16.
(2)在扇形统计图中,D小组对应的圆心角的度数是360°×=126°.
故答案为126.
(3)c=200×25%=50.
故答案为50.
补全的频数分布直方图如图所示.
(4)2000×=940(人),
即估计该校学生成绩为优秀的有940人.
2
(建议用时:90分钟 分值:100分)
一、选择题(本大题共10小题,每小题3分,满分30分)
1.下列调查中,最适合采用抽样调查的是( )
A.调查一批灯泡的质量
B.调查某校初一一班同学的视力
C.为保证某种新研发的大型客机试飞成功,对其零部件进行检查
D.对乘坐某班次飞机的乘客进行安检
2.下列统计图中,最宜反映气温变化的是( )
A.折线统计图 B.条形统计图 C.扇形统计图 D.频数分布直方图
3.为了解七年级4000名学生参加数学测试成绩的情况,从中随机抽取200名学生的数学成绩进行分析.下列说法正确的是( )
A.样本容量是200名 B.每名学生是个体
C.200名学生的数学成绩是总体的一个样本 D.4000名学生是总体
4.某公司今年7月1日~5日每天用水量变化情况如图所示,若设这5天的日最高用水量为a立方米,日最低用水量为b立方米,则a-b的值为( )
A.4 B.6 C.8 D.10
5.为了解游客在云台山、神农山和青天河这三个风景区旅游的满意率,数学小组的同学商议了几个收集数据的方案.方案一:在多家旅游公司调查300名导游.方案二:在云台山景区调查300名游客.方案三:在神农山景区调查300名游客.方案四:在三个景区各调查100名游客.其中最合理的方案是( )
A.方案一 B.方案二 C.方案三 D.方案四
6.春节前夕,学校向2000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹.B类:少放烟花爆竹.C类:使用电子鞭炮.D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,估计全校“使用电子鞭炮”的学生有( )
A.200名 B.400名 C.600名 D.750名
7.李老师对本班60名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别 A型 B型 O型 AB型
百分比 f 35% 15% 10%
A.6 B.9 C.21 D.24
8.为了解七年级学生的体能情况,抽取了某校该年级的部分学生进行一分钟跳绳测试,将所得数据整理后,画成如图所示的统计图,从左到右前三个小组所占的百分比分别为10%,30%,40%,从左至右第一小组若有5人,则第四小组的人数是( )
A.8 B.9 C.10 D.15
9.为加强锻炼增强体魄,我校初三(1)班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与各活动小组人数分布情况的扇形图和条形图如图所示,有下列说法:
①该班共有50名学生;
②篮球小组有16人;
③跳绳小组人数所占扇形圆心角为57.6°;
④足球小组人数所占扇形圆心角为120°.
这四种说法中正确的有( )
A.2个 B.0个 C.1个 D.3个
10.自来水公司调查了部分用户的月用水量(吨),按月用水量将用户分成A,B,C,D,E五组进行统计.并制作了如图所示的扇形统计图,已知参与调查的用户共有80户,则所有参与调查的用户中用水量在6吨以下的共有( )
组别 月用水量x/吨
A 0≤x<3
B 3≤x<6
C 6≤x<9
D 9≤x<12
E x≥12
A.18户 B.20户 C.22户 D.24户
二、填空题(本大题共4小题,每小题3分,满分12分)
11.为了了解某校七年级1500名学生的数学期中考试成绩,从中抽取了200名学生的成绩进行统计,在这个问题中,样本容量是_____.
12.统计得到的一组数据的最大值是218,最小值是100.若确定组距为15,则可以分成___组.
13.某校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目.为了了解全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中一个项目),并把调查结果绘制成如图所示的统计图,根据这个统计图可以估计该学校150名学生中选择篮球项目的学生为____名.
14.小文同学统计了他所在小区居民每天手机阅读的时间,并绘制了直方图,有下列说法:
①小文同学一共统计了60人;
②每天手机阅读不足20分钟的有8人;
③每天手机阅读30~40分钟的人数最多;
④每天手机阅读0~10分钟的人数最少.
根据图中信息,上述说法中正确的是____.(填写序号)
三、解答题(本大题共8小题,满分58分)
15.(6分)为了考察某市1万名初中生视力情况,从中抽取1000人进行视力检测,这个问题中总体、个体、样本、样本容量分别是什么
16.(6分)琪琪想了解全市八年级学生每天写作业的时间,她对某校八年级(4)班全体学生每天写作业的时间进行了一次调查.
(1)调查的问题是什么
(2)调查的范围有多大 用了哪种调查方式
17.(6分)为了考察4名篮球运动员投篮的命中率,让每名运动员投篮10次.
(1)你认为需要获取哪些数据 如何去获取这些数据
(2)记录员记下这4名篮球运动员投篮命中次数如下:
甲:正;乙:正;丙:正;丁:正正.
请将数据整理后填写下表.
篮球运动员 甲 乙 丙 丁
命中次数 ___ ___ ___ ___
命中率(%) ___ ___ ___ ___
18.(7分)观察如图所示的扇形统计图,然后解答问题.
(1)已知西红柿的种植面积是4.2公顷,三种蔬菜种植的总面积是____公顷.
(2)黄瓜的种植面积是___公顷.
(3)求茄子的种植面积是西红柿种植面积的百分之几.
19.(7分)网瘾低龄化问题已引起社会各界的高度关注,有关部门在全国范围内对12~35岁的网瘾人群进行简单随机抽样调查并得到如图所示的统计图,其中30~35岁的网瘾人数占样本人数的20%.
(1)请把图中缺失的数据、图形补充完整.
(2)若12~35岁的网瘾人数约为4000,请你根据图中数据估计网瘾人群中12~17岁的网瘾人数.
20.(8分)某校的20年校庆举办了四个项目的比赛,现分别以A,B,C,D表示它们.要求每位同学必须参加且限报一项.以七(1)班为样本进行统计,并将统计结果绘制成两幅统计图,其中参加A项目的人数比参加C与D项目人数的总和多1人,参加D项目的人数比参加A项目的人数少11人.请你结合图中所给出的信息解答下列问题:
(1)求出全班总人数;
(2)求出扇形统计图中参加D项目的学生所在的扇形圆心角的度数.
21.(8分)某校八年级共有8个班,241名同学,书法老师为了解该校八年级学生选修书法的意向,请小红、小亮、小军三位同学分别进行抽样调查.三位同学调查结果反馈如下:
(1)小红、小亮和小军三人中,你认为哪位同学的调查结果较好地反映了该校八年级同学选修书法的意向,并说出理由.
(2)估计八年级有意向选修书法的同学的人数.
22.(10分)“青年大学习”是共青团中央为组织引导广大青少年,深入学习贯彻习近平新时代中国特色社会主义思想和党的二十大精神的学习平台.我区某中学为了解学生的“青年大学习”的学习情况,组织了“青年大学习”知识竞赛,从中抽取了部分学生成绩进行统计(成绩均为整数,满分100分),按照成绩分成A,B,C,D,E五个小组,并绘制成不完整的统计表和统计图.
组别 分数段/分 频数/人数
A 50.5~60.5 a
B 60.5~70.5 40
C 70.5~80.5 c
D 80.5~90.5 70
E 90.5~100.5 24
合计 b
请结合上述信息完成下列问题:
(1)b=____,a=____;
(2)在扇形统计图中,D小组对应的圆心角的度数是____°;
(3)c=____,并补全频数分布直方图;
(4)若全校有2000名学生,成绩在80分以上(不含80分)为优秀,根据抽样调查结果,请估计该校学生成绩为优秀的人数.
参考答案
1.A 2.A 3.C 4.C 5.D 6.B 7.D 8.C 9.C
10.D 11.200 12.8 13.30 14.③④
15.【解析】总体:某市1万名初中生视力情况;
个体:每个初中生的视力情况;
样本:抽取的1000初中生的视力情况;
样本容量:1000.
16.【解析】(1)调查的问题是全市八年级学生每天写作业的时间.
(2)调查的范围是某校八年级(4)班全体学生,用了抽样调查方式.
17.【解析】(1)需要获取每位运动员投篮10次命中的次数,
可以让4名篮球运动员在相同的条件下进行投篮,记录每位运动员投篮10次命中的次数.
(2)将数据整理后填写表格如下.
篮球运动员 甲 乙 丙 丁
命中次数 9 6 8 10
命中率(%) 90% 60% 80% 100%
18.【解析】(1)三种蔬菜种植的总面积是4.2÷56%=7.5(公顷).
故答案为7.5.
(2)黄瓜的种植面积是7.5×30%=2.25(公顷).
故答案为2.25.
(3)茄子的种植面积是西红柿种植面积的×100%=25%.
19.【解析】(1)∵被调查的总人数为480÷20%=2400,
∴12~17岁的网瘾人数为2400-600-576-480=744(人),
补全图形如下:
(2)744÷2400×100%=31%,
4000×31%=1240(人),
∴若12~35岁的网瘾人数约为4000,则根据图中数据估计网瘾人群中12~17岁的网瘾人数是1240.
20.【解析】(1)全班的总人数为25÷50%=50.
答:全班的人数为50.
(2)设参加D项目的人数为x,C项目的人数为y,则A项目的人数为(x+11).
依题意得解得
所以参加D项目的人数为2,
所以参加D项目的学生所在的扇形圆心角的度数为×360°=14.4°.
答:在扇形统计图中参加D项目的学生所在的扇形圆心角的度数为14.4°.
21.【解析】(1)小军的数据较好地反映了该校八年级同学选修书法的意向.
理由如下:
小红仅调查了一个班的同学,样本不具有随机性;
小亮只调查了8位语文课代表,样本容量过少,不具有代表性;
小军的调查样本容量适中,且能够代表八年级的同学的选择意向.
(2)根据小军的调查结果,有意向选择书法的比例约为=,
故据此估计八年级有意向选修书法的同学人数为241×=60.25≈60.
22.【解析】(1)b=40÷20%=200,a=200×8%=16.
故答案为200;16.
(2)在扇形统计图中,D小组对应的圆心角的度数是360°×=126°.
故答案为126.
(3)c=200×25%=50.
故答案为50.
补全的频数分布直方图如图所示.
(4)2000×=940(人),
即估计该校学生成绩为优秀的有940人.
2
