2015沪科版九年级上册数学单元梯度检测精品卷:(一)第21章二次函数与反比例函数单元梯度检测A卷
文档属性
| 名称 | 2015沪科版九年级上册数学单元梯度检测精品卷:(一)第21章二次函数与反比例函数单元梯度检测A卷 |  | |
| 格式 | zip | ||
| 文件大小 | 270.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-22 13:16:48 | ||
图片预览



文档简介
(一)第21章二次函数与反比例函数单元梯度检测A卷
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.抛物线y=﹣3(x-1)2+27与x轴交点的横坐标为…………………………………【 】
A.±3 B.4或﹣2 C.6 D.0
2. 抛物线y=﹣x2-2 x+1的顶点坐标是……………………………………………【 】
A.(﹣1,2) B.(1,2) C.(﹣1,﹣2) D.(1,﹣2)
3.二次函数y=ax2+b x+c的图象如图所示,则下列结论不正确的是………………【 】
A.abc<0 B.a-b+c>0 C. ﹣2<﹣ <﹣1 D. 2a-b=0
4.如图,是我校第六届校运会上铅球项目冠军梦甲运动员掷铅球的高度ym与水平距离xm之间的函数关系式y=﹣x2+x+3的图象,则梦甲此次掷铅球的成绩是………………………………………………………………………………………【 】
A.7m B.8m C.9m D.10m
5.如图,M,N是反比例函数y=图象上的两点,分别过M,N作x轴,y轴的垂线,构成图中的三个相邻且不重叠的小矩形S1,S2,S3.已知S1+S3=6,则S2=………【 】
A.1 B.2 C.3 D.4
6.若直线y=ax+b 经过第二、三、四象限,则抛物线y=ax2+bx的对称轴一定在………………………………………………………………………………………【 】
A.y轴左侧 B. y轴 C. y轴右侧 D.不确定
7.将抛物线y=ax2+b x+c先向左平移1个单位,再向下平移2个单位,得到新的抛物线y=﹣x2-2x+3,则…………………………………………………………………【 】
A.b=4,c=﹣2 B. b=﹣4,c=2 C. b=﹣2,c=6 D. b=﹣1,c=4
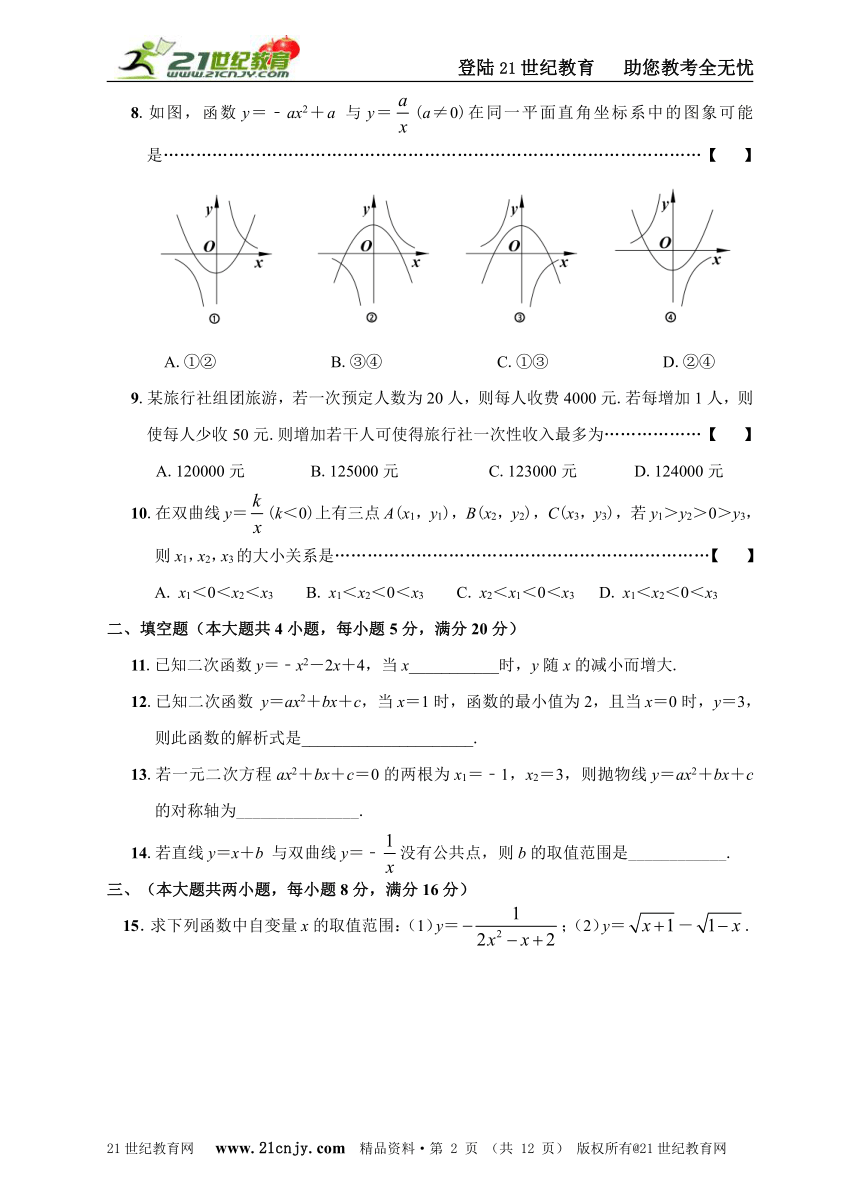
8.如图,函数y=﹣ax2+a 与y=(a≠0)在同一平面直角坐标系中的图象可能是………………………………………………………………………………………【 】
A.①② B.③④ C.①③ D.②④
9.某旅行社组团旅游,若一次预定人数为20人,则每人收费4000元.若每增加1人,则使每人少收50元.则增加若干人可使得旅行社一次性收入最多为………………【 】
A.120000元 B.125000元 C.123000元 D.124000元
10.在双曲线y=(k<0)上有三点A(x1,y1),B(x2,y2),C(x3,y3),若y1>y2>0>y3,则x1,x2,x3的大小关系是……………………………………………………………【 】
A. x1<0<x2<x3 B. x1<x2<0<x3 C. x2<x1<0<x3 D. x1<x2<0<x3
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知二次函数y=﹣x2-2x+4,当x___________时,y随x的减小而增大.
12.已知二次函数 y=ax2+bx+c,当x=1时,函数的最小值为2,且当x=0时,y=3,则此函数的解析式是_____________________.21·世纪*教育网
13.若一元二次方程ax2+bx+c=0的两根为x1=﹣1,x2=3,则抛物线y=ax2+bx+c的对称轴为_______________.www-2-1-cnjy-com
14.若直线y=x+b 与双曲线y=﹣没有公共点,则b的取值范围是____________.
三、(本大题共两小题,每小题8分,满分16分)
15.求下列函数中自变量x的取值范围:(1)y=;(2)y=-.
16.用配方法求抛物线y=x2-3x+的顶点坐标,并说明x取何值时,y随x的增大而减小.
四、(本大题共两小题,每小题8分,满分16分)
17.求经过点A(2,3)和点B(﹣1,5)的抛物线y=ax2+bx+c的一个解析式.
18.已知1-y与x+7成反比例,且当x=﹣3时,y=4,求y与x之间的函数关系式.
五、(本大题共两小题,每小题10分,满分20分)
19.画出函数y=﹣x2-x+的图象,设抛物线与x轴交于点A,B(点A在点B的左边),与y轴交于点C,其顶点为D,求四边形ABCD的面积.
20.如图,A,B是反比例函数y=(x>0)图象上的两点,点A,B的横坐标分别为1,2,求△AOB的面积.2-1-c-n-j-y
六、(本题满分12分)
21.如图,抛物线y=ax2+4x+c经过坐标原点O,与x轴交于点A(4,0),顶点为点B.
(1)分别求直线AB与抛物线的解析式;
(2)在抛物线上是否存在点P,使S△AOP=6,若存在,请求出点P的坐标;若不存在,请说明理由.
七、(本题满分12分)
22.如图,双曲线y=与直线AB交于点A,B,点A坐标为(﹣1,4),点B的横坐标为4.
(1)求△AOB的面积;
(2)根据图象,直接写出一次函数值大于反比例函数值时自变量x的取值范围.
八、(本题满分14分)
23.某家电商场将每台进价为3000元的液晶彩电以3900元的售价出售,每天可售出6台,若这种品牌的液晶彩电每台降价100x元(x为正整数),则每天可多售出3x台.试问该品牌液晶彩电的售价定为多少时,每天获得的利润最大?最大利润是多少?
参考答案
1.B 解析:由y=0得﹣3(x-1)2+27=0,解得x=4或﹣2
2.A 解析:由配方法得y=﹣x2-2 x+1=﹣(x+1)2+2
3.D 解析:由图象得a<0,b<0,c<0,∴abc<0,A对;当x=﹣1时,y=a-b+c>0,∴B对;∵x1=﹣2,﹣2<x2<0,∴﹣2<<﹣1,即﹣2<﹣ <﹣1,∴C对;∵a<0,﹣ <﹣1,∴b<2a,∴2a-b>0,∴D错
4.C 解析:由题意,y=0,∴﹣x2+x+3=0,解得x1=9,x2=﹣2(不合题意,舍去) 5.B 解析:∵点M,N都在双曲线y=上,∴可得S1+S2=S2+S3=5,∴S1+2S2+S3=
10,又 S1+S3=6,∴S2=2
6.A 解析:∵直线y=ax+b 经过第二、三、四象限,∴a<0,b<0,∴﹣ <0,∴抛物线对称轴直线x=﹣ 在y轴左侧 21世纪教育网版权所有
7.B 解析:将抛物线y=﹣x2-2x+3=﹣(x+1)2+4先向右平移1个单位,再向上平移2个单位,得抛物线y=﹣(x+2)2+6=﹣x2-4x+2,∴b=﹣4,c=2
8.D 解析:当a>0时,抛物线开口向下,双曲线在第一、三象限,②对;当a<0时,抛物线开口向上,双曲线在第二、四象限,④对,∴D对
9.B 解析:设增加x人,旅行社一次性收入y元,由题意得y=(20+x)(4000-50x)=﹣50(x-30)2+125000,∴当x=30时,y最大=125000,∴B对
10.C 解析:在同一坐标系中描出A,B,C三点大致位置如下图,由y1>y2>0>y3,可得x2<x1<0<x3,∴C对21cnjy.com
11.>﹣1 解析:∵a=﹣1<0,∴在对称轴右侧,y随x的增大而减小,又∵对称轴为直线x=﹣=1,∴当x>﹣1时,y随x的减小而增大
12. y=x2-2 x+3 解析:∵当x=1时,函数的最小值为2,∴可设y=a(x-1)2+2,又当x=0时,y=3,∴代入解得a=1,∴y=(x-1)2+2=x2-2x+3,
13.直线x=1 解析:由韦达定理得,x1+x2=﹣1+3=2=﹣,∴抛物线的对称轴为直线x=﹣=2×=1 21·cn·jy·com
14.﹣2<x<2 解析:由题意得x+b=﹣,化简得x2+bx+1=0,△=b2-4,∵两图象没有公共点,∴△<0,∴b2-4<0,解得﹣2<x<2
15.解:(1)由题意得2x2-x+2≠0,又∵2x2-x+2=2(x-)2+≠0,∴自变量x的取值范围是全体实数;www.21-cn-jy.com
(2)由题意得,解得﹣1≤x≤1,∴自变量x的取值范围是﹣1≤x≤1.
16.解:由配方法得,y=x2-3x+=(x2-6x)+=(x-3)2-1,∴此抛物线的顶点坐标(3,﹣1),∵a=>0,∴当x<3时,y随x的增大而减小.
17.答案不唯一,如:解: 把点A(2,3),B(﹣1,5)的坐标分别代入y=ax2+bx+c得,①-②得3a+3b=﹣2,令a=1,则b=﹣,把a=1,b=﹣代入②得c=,∴所求抛物线的一个解析式为y=x2-x+21教育网
18.解:∵1-y与x+7成反比例,∴可设1-y=,把x=﹣3,y=4代入得1-4=,解得k=﹣12,∴1-y=,∴y与x之间的函数关系式为y=+1.
当y=0时,﹣x2-x+=0,解得x1=﹣3,x2=1,
∴A点坐标为(﹣3,0),B点坐标为(1,0),
∴S四边形ABCD=S△AED+S梯形DEOC+S△COB
=×2×2+×(+2)×1+×1×
=4.5.
20.解:如下图,分别过点A作AC⊥y轴于点C,AD⊥x轴于点D,过点B作BE⊥x轴于点E,把x=1,x=2分别代入y=得y=4,y=2,∴A点坐标为(1,4),B点坐标为(2,2),∴S五边形COEBA=S矩形CODA+S梯形ADEB=4+×(4+2)×2=10,∴S△AOB=S五边形COEBA―S△AOBC―S△EOB=10-2-2=6.2·1·c·n·j·y
21.解:(1)把点O(0,0),A(4,0)的坐标分别代入y=ax2+4x+c得,解得a=﹣1,c=0,∴抛物线的解析式为y=﹣x2+4x;【来源:21·世纪·教育·网】
∵y=﹣x2+4x=﹣(x-2)2+4,∴顶点B的坐标为(2,4),
设直线AB的解析式为y=kx+b,把A,B两点的坐标分别代入得,解得k=﹣2,b=8,
∴直线AB的解析式为y=﹣2x+8.
(2)存在点P,如下图所示,设P点坐标为(x,y),
∵S△AOP=6,∴×4×=6,解得y=±3,
当y=3时,﹣x2+4x=3,解得x=1或3;
当x=﹣3时,﹣x2+4x=﹣3,解得x=2±,
∴P点坐标为(1,3)或(3,3)或(2+,﹣3)或(2-,﹣3).
22.(1)把点A(﹣1,4)的坐标代入y=得k=﹣4,∴y=﹣,当x=4时,y=﹣1,∴B点坐标为(4,﹣1),设直线AB的解析式为y=kx+b,把A,B两点的坐标分别代入得,解得k=﹣1,b=3,∴直线AB的解析式为y=﹣x+3,如下图,设直线AB与y轴交于点C,当x=0时,y=3,∴C点坐标为(0,3),∴S△AOB=S△AOC+S△BOC=×3×1+×3×4=7.5;
(2)x<﹣1或0<x<4.
23.解:设商场每天获得的利润为y元,
由题意得,y=(6+3x)(3900-3000-100x)
=﹣300x2+2100x+5400
=﹣300(x-3.5)2+9075,
∵a=﹣300<0,x又为正整数,
∴当x=3或4时,y最大=﹣300(3-3.5)2+9075=9000,
此时售价为3900-100×3=3600(元)或3900-100×4=3500(元),
答:该品牌液晶彩电的售价定为3500元或3600元时,每天获得的利润最大,最大利润是9000元.
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.抛物线y=﹣3(x-1)2+27与x轴交点的横坐标为…………………………………【 】
A.±3 B.4或﹣2 C.6 D.0
2. 抛物线y=﹣x2-2 x+1的顶点坐标是……………………………………………【 】
A.(﹣1,2) B.(1,2) C.(﹣1,﹣2) D.(1,﹣2)
3.二次函数y=ax2+b x+c的图象如图所示,则下列结论不正确的是………………【 】
A.abc<0 B.a-b+c>0 C. ﹣2<﹣ <﹣1 D. 2a-b=0
4.如图,是我校第六届校运会上铅球项目冠军梦甲运动员掷铅球的高度ym与水平距离xm之间的函数关系式y=﹣x2+x+3的图象,则梦甲此次掷铅球的成绩是………………………………………………………………………………………【 】
A.7m B.8m C.9m D.10m
5.如图,M,N是反比例函数y=图象上的两点,分别过M,N作x轴,y轴的垂线,构成图中的三个相邻且不重叠的小矩形S1,S2,S3.已知S1+S3=6,则S2=………【 】
A.1 B.2 C.3 D.4
6.若直线y=ax+b 经过第二、三、四象限,则抛物线y=ax2+bx的对称轴一定在………………………………………………………………………………………【 】
A.y轴左侧 B. y轴 C. y轴右侧 D.不确定
7.将抛物线y=ax2+b x+c先向左平移1个单位,再向下平移2个单位,得到新的抛物线y=﹣x2-2x+3,则…………………………………………………………………【 】
A.b=4,c=﹣2 B. b=﹣4,c=2 C. b=﹣2,c=6 D. b=﹣1,c=4
8.如图,函数y=﹣ax2+a 与y=(a≠0)在同一平面直角坐标系中的图象可能是………………………………………………………………………………………【 】
A.①② B.③④ C.①③ D.②④
9.某旅行社组团旅游,若一次预定人数为20人,则每人收费4000元.若每增加1人,则使每人少收50元.则增加若干人可使得旅行社一次性收入最多为………………【 】
A.120000元 B.125000元 C.123000元 D.124000元
10.在双曲线y=(k<0)上有三点A(x1,y1),B(x2,y2),C(x3,y3),若y1>y2>0>y3,则x1,x2,x3的大小关系是……………………………………………………………【 】
A. x1<0<x2<x3 B. x1<x2<0<x3 C. x2<x1<0<x3 D. x1<x2<0<x3
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知二次函数y=﹣x2-2x+4,当x___________时,y随x的减小而增大.
12.已知二次函数 y=ax2+bx+c,当x=1时,函数的最小值为2,且当x=0时,y=3,则此函数的解析式是_____________________.21·世纪*教育网
13.若一元二次方程ax2+bx+c=0的两根为x1=﹣1,x2=3,则抛物线y=ax2+bx+c的对称轴为_______________.www-2-1-cnjy-com
14.若直线y=x+b 与双曲线y=﹣没有公共点,则b的取值范围是____________.
三、(本大题共两小题,每小题8分,满分16分)
15.求下列函数中自变量x的取值范围:(1)y=;(2)y=-.
16.用配方法求抛物线y=x2-3x+的顶点坐标,并说明x取何值时,y随x的增大而减小.
四、(本大题共两小题,每小题8分,满分16分)
17.求经过点A(2,3)和点B(﹣1,5)的抛物线y=ax2+bx+c的一个解析式.
18.已知1-y与x+7成反比例,且当x=﹣3时,y=4,求y与x之间的函数关系式.
五、(本大题共两小题,每小题10分,满分20分)
19.画出函数y=﹣x2-x+的图象,设抛物线与x轴交于点A,B(点A在点B的左边),与y轴交于点C,其顶点为D,求四边形ABCD的面积.
20.如图,A,B是反比例函数y=(x>0)图象上的两点,点A,B的横坐标分别为1,2,求△AOB的面积.2-1-c-n-j-y
六、(本题满分12分)
21.如图,抛物线y=ax2+4x+c经过坐标原点O,与x轴交于点A(4,0),顶点为点B.
(1)分别求直线AB与抛物线的解析式;
(2)在抛物线上是否存在点P,使S△AOP=6,若存在,请求出点P的坐标;若不存在,请说明理由.
七、(本题满分12分)
22.如图,双曲线y=与直线AB交于点A,B,点A坐标为(﹣1,4),点B的横坐标为4.
(1)求△AOB的面积;
(2)根据图象,直接写出一次函数值大于反比例函数值时自变量x的取值范围.
八、(本题满分14分)
23.某家电商场将每台进价为3000元的液晶彩电以3900元的售价出售,每天可售出6台,若这种品牌的液晶彩电每台降价100x元(x为正整数),则每天可多售出3x台.试问该品牌液晶彩电的售价定为多少时,每天获得的利润最大?最大利润是多少?
参考答案
1.B 解析:由y=0得﹣3(x-1)2+27=0,解得x=4或﹣2
2.A 解析:由配方法得y=﹣x2-2 x+1=﹣(x+1)2+2
3.D 解析:由图象得a<0,b<0,c<0,∴abc<0,A对;当x=﹣1时,y=a-b+c>0,∴B对;∵x1=﹣2,﹣2<x2<0,∴﹣2<<﹣1,即﹣2<﹣ <﹣1,∴C对;∵a<0,﹣ <﹣1,∴b<2a,∴2a-b>0,∴D错
4.C 解析:由题意,y=0,∴﹣x2+x+3=0,解得x1=9,x2=﹣2(不合题意,舍去) 5.B 解析:∵点M,N都在双曲线y=上,∴可得S1+S2=S2+S3=5,∴S1+2S2+S3=
10,又 S1+S3=6,∴S2=2
6.A 解析:∵直线y=ax+b 经过第二、三、四象限,∴a<0,b<0,∴﹣ <0,∴抛物线对称轴直线x=﹣ 在y轴左侧 21世纪教育网版权所有
7.B 解析:将抛物线y=﹣x2-2x+3=﹣(x+1)2+4先向右平移1个单位,再向上平移2个单位,得抛物线y=﹣(x+2)2+6=﹣x2-4x+2,∴b=﹣4,c=2
8.D 解析:当a>0时,抛物线开口向下,双曲线在第一、三象限,②对;当a<0时,抛物线开口向上,双曲线在第二、四象限,④对,∴D对
9.B 解析:设增加x人,旅行社一次性收入y元,由题意得y=(20+x)(4000-50x)=﹣50(x-30)2+125000,∴当x=30时,y最大=125000,∴B对
10.C 解析:在同一坐标系中描出A,B,C三点大致位置如下图,由y1>y2>0>y3,可得x2<x1<0<x3,∴C对21cnjy.com
11.>﹣1 解析:∵a=﹣1<0,∴在对称轴右侧,y随x的增大而减小,又∵对称轴为直线x=﹣=1,∴当x>﹣1时,y随x的减小而增大
12. y=x2-2 x+3 解析:∵当x=1时,函数的最小值为2,∴可设y=a(x-1)2+2,又当x=0时,y=3,∴代入解得a=1,∴y=(x-1)2+2=x2-2x+3,
13.直线x=1 解析:由韦达定理得,x1+x2=﹣1+3=2=﹣,∴抛物线的对称轴为直线x=﹣=2×=1 21·cn·jy·com
14.﹣2<x<2 解析:由题意得x+b=﹣,化简得x2+bx+1=0,△=b2-4,∵两图象没有公共点,∴△<0,∴b2-4<0,解得﹣2<x<2
15.解:(1)由题意得2x2-x+2≠0,又∵2x2-x+2=2(x-)2+≠0,∴自变量x的取值范围是全体实数;www.21-cn-jy.com
(2)由题意得,解得﹣1≤x≤1,∴自变量x的取值范围是﹣1≤x≤1.
16.解:由配方法得,y=x2-3x+=(x2-6x)+=(x-3)2-1,∴此抛物线的顶点坐标(3,﹣1),∵a=>0,∴当x<3时,y随x的增大而减小.
17.答案不唯一,如:解: 把点A(2,3),B(﹣1,5)的坐标分别代入y=ax2+bx+c得,①-②得3a+3b=﹣2,令a=1,则b=﹣,把a=1,b=﹣代入②得c=,∴所求抛物线的一个解析式为y=x2-x+21教育网
18.解:∵1-y与x+7成反比例,∴可设1-y=,把x=﹣3,y=4代入得1-4=,解得k=﹣12,∴1-y=,∴y与x之间的函数关系式为y=+1.
当y=0时,﹣x2-x+=0,解得x1=﹣3,x2=1,
∴A点坐标为(﹣3,0),B点坐标为(1,0),
∴S四边形ABCD=S△AED+S梯形DEOC+S△COB
=×2×2+×(+2)×1+×1×
=4.5.
20.解:如下图,分别过点A作AC⊥y轴于点C,AD⊥x轴于点D,过点B作BE⊥x轴于点E,把x=1,x=2分别代入y=得y=4,y=2,∴A点坐标为(1,4),B点坐标为(2,2),∴S五边形COEBA=S矩形CODA+S梯形ADEB=4+×(4+2)×2=10,∴S△AOB=S五边形COEBA―S△AOBC―S△EOB=10-2-2=6.2·1·c·n·j·y
21.解:(1)把点O(0,0),A(4,0)的坐标分别代入y=ax2+4x+c得,解得a=﹣1,c=0,∴抛物线的解析式为y=﹣x2+4x;【来源:21·世纪·教育·网】
∵y=﹣x2+4x=﹣(x-2)2+4,∴顶点B的坐标为(2,4),
设直线AB的解析式为y=kx+b,把A,B两点的坐标分别代入得,解得k=﹣2,b=8,
∴直线AB的解析式为y=﹣2x+8.
(2)存在点P,如下图所示,设P点坐标为(x,y),
∵S△AOP=6,∴×4×=6,解得y=±3,
当y=3时,﹣x2+4x=3,解得x=1或3;
当x=﹣3时,﹣x2+4x=﹣3,解得x=2±,
∴P点坐标为(1,3)或(3,3)或(2+,﹣3)或(2-,﹣3).
22.(1)把点A(﹣1,4)的坐标代入y=得k=﹣4,∴y=﹣,当x=4时,y=﹣1,∴B点坐标为(4,﹣1),设直线AB的解析式为y=kx+b,把A,B两点的坐标分别代入得,解得k=﹣1,b=3,∴直线AB的解析式为y=﹣x+3,如下图,设直线AB与y轴交于点C,当x=0时,y=3,∴C点坐标为(0,3),∴S△AOB=S△AOC+S△BOC=×3×1+×3×4=7.5;
(2)x<﹣1或0<x<4.
23.解:设商场每天获得的利润为y元,
由题意得,y=(6+3x)(3900-3000-100x)
=﹣300x2+2100x+5400
=﹣300(x-3.5)2+9075,
∵a=﹣300<0,x又为正整数,
∴当x=3或4时,y最大=﹣300(3-3.5)2+9075=9000,
此时售价为3900-100×3=3600(元)或3900-100×4=3500(元),
答:该品牌液晶彩电的售价定为3500元或3600元时,每天获得的利润最大,最大利润是9000元.
