2015沪科版九年级上册数学单元梯度检测精品卷:(二)第21章二次函数与反比例函数单元梯度检测B卷
文档属性
| 名称 | 2015沪科版九年级上册数学单元梯度检测精品卷:(二)第21章二次函数与反比例函数单元梯度检测B卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 339.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-22 00:00:00 | ||
图片预览


文档简介
(二)第21章二次函数与反比例函数单元梯度检测B卷
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.抛物线y=ax2+b x﹣2经过点(﹣3,5),则a-b-的值为……………………【 】
A. B. C. D.
2.关于x的一元二次方程x2-x+n=0有两个不相等的实数根,则抛物线y=x2-x+n的顶点一定在……………………………………………………………………………【 】
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知函数y=(a+2)x2-2x+1的图象与x轴有交点,则a的取值范围是…………【 】
A.a≤﹣1 B. a≤﹣1且a≠﹣2 C. a<﹣1 D. a<﹣1且a≠﹣2
4.如图,某函数的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是直线x=﹣1,则下列结论:①抛物线的顶点坐标为(﹣1,4);②此函数的解析式为y=﹣x2-2x+3;③当x<0时,y随x的增大而增大;④抛物线与x轴的另一个交点是(﹣3,0).其中正确的有………………………………………………………………【 】
A.①② B.①②③ C.①②④ D.②③④
5.某种气球内充满一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V(m3)的反比例函数,其图象如图,当气球内的气压大于100 kPa时,气球将爆炸,为了安全,气球的体积应满足的条件是………………………………………【 】
A.不大于m3 B. 不小于m3 C. 大于m3 D. 小于m3
6.如图,是二次函数y=ax2+bx+c的图象,小元同学认真观察图象,获得如下四条信息:①b2-4ac>0;②2a+b>0;③a+b+c<0;④当y=﹣1时,方程ax2+b x+c=﹣1的两根均为正数.其中不正确的是………………………………………………【 】
A.① B.② C.③ D.④
7.已知抛物线y=x2+bx+c经过点(0,﹣2),若要使该抛物线与x轴的一个交点在(﹣3,0)和(﹣1,0)之间,则抛物线的解析式不可能是……………………………【 】
A. y=x2-2 B. y=x2+x-2 C. y=x2+2x-2 D. y=x2+3x-2
8.甲、乙两人进行羽毛球比赛,最后关头,甲发出一个十分关键的球,球的出手点为M,球距地面高度h(m)与其飞出的水平距离s(m)之间的关系式为h=﹣s2+s+,如图所示,已知球网AB距原点5m,乙(用线段EF表示)扣球的最大高度为2m,设乙的起跳点E的横坐标为a,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则a的取值范围是………………………………………………【 】
A.a>5 B.5<a<6 C. 5<a<4+ D. 5<a<4+
9.在今年的六一儿童节期间,我校举行了七、八年级“庆六一”篮球友谊赛.如图是我班阿文同学某次投球时的篮球运动路线图,可以看做是抛物线y=﹣x2+b x+c的一部分,其中出球点A离地面O点的距离为1.5m,篮球落地点B离O点的距离是3m,则此次投球中篮球达到的最大高度是………………………………………………【 】
A.1m B. 2m C. 3m D. 4m
10.如图,四边形OABC是菱形,点A在x轴上,直线y=x经过点C,菱形OABC的面积为2,过BC中点D的双曲线的解析式为……………………………………【 】
A. y= B. y= C. y= D. y=
二、填空题(本大题共4小题,每小题5分,满分20分)
11.请写出一个开口向下,与y轴交点的纵坐标为﹣1,且经过点(2,1)的抛物线的解析式为___________________________.2-1-c-n-j-y
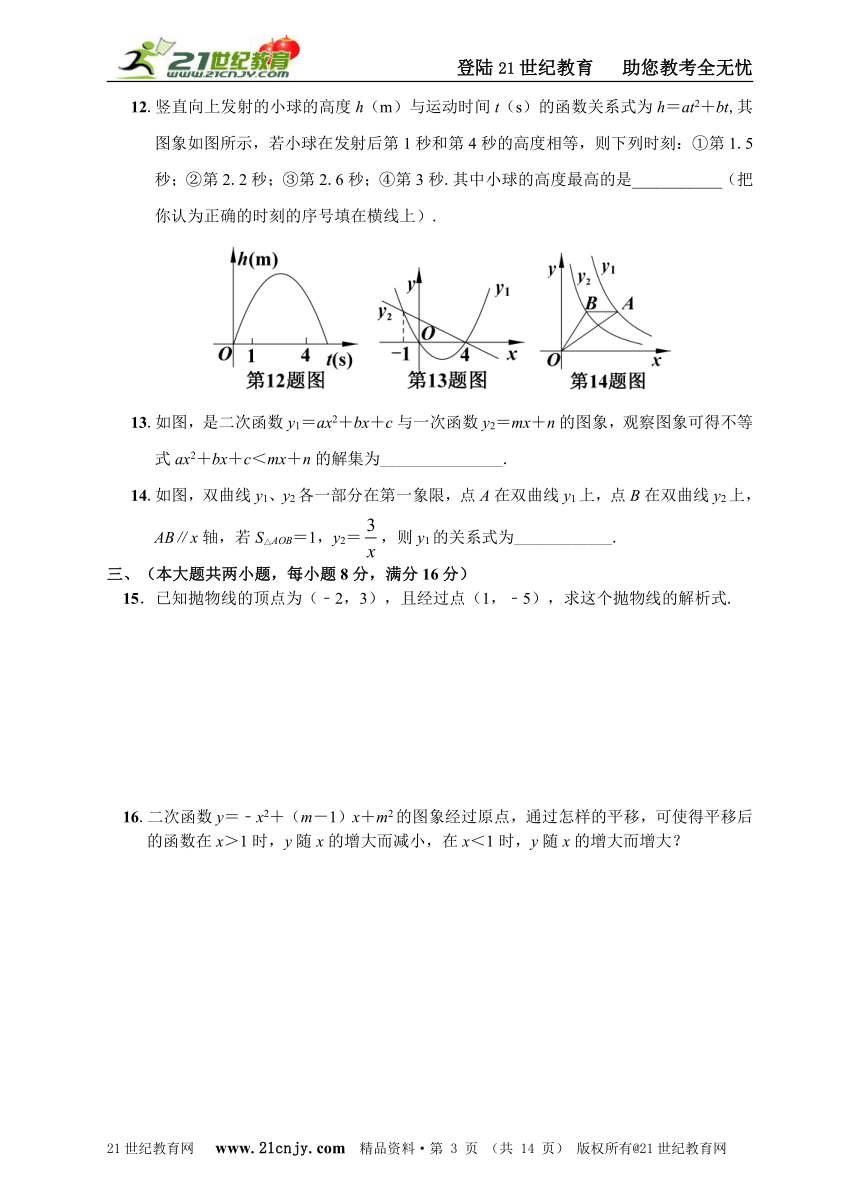
12.竖直向上发射的小球的高度h(m)与运动时间t(s)的函数关系式为h=at2+bt,其图象如图所示,若小球在发射后第1秒和第4秒的高度相等,则下列时刻:①第1.5秒;②第2.2秒;③第2.6秒;④第3秒.其中小球的高度最高的是___________(把你认为正确的时刻的序号填在横线上).
13.如图,是二次函数y1=ax2+bx+c与一次函数y2=mx+n的图象,观察图象可得不等式ax2+bx+c<mx+n的解集为_______________.
14.如图,双曲线y1、y2各一部分在第一象限,点A在双曲线y1上,点B在双曲线y2上,AB∥x轴,若S△AOB=1,y2=,则y1的关系式为____________.
三、(本大题共两小题,每小题8分,满分16分)
15.已知抛物线的顶点为(﹣2,3),且经过点(1,﹣5),求这个抛物线的解析式.
16.二次函数y=﹣x2+(m-1)x+m2的图象经过原点,通过怎样的平移,可使得平移后的函数在x>1时,y随x的增大而减小,在x<1时,y随x的增大而增大?
四、(本大题共两小题,每小题8分,满分16分)
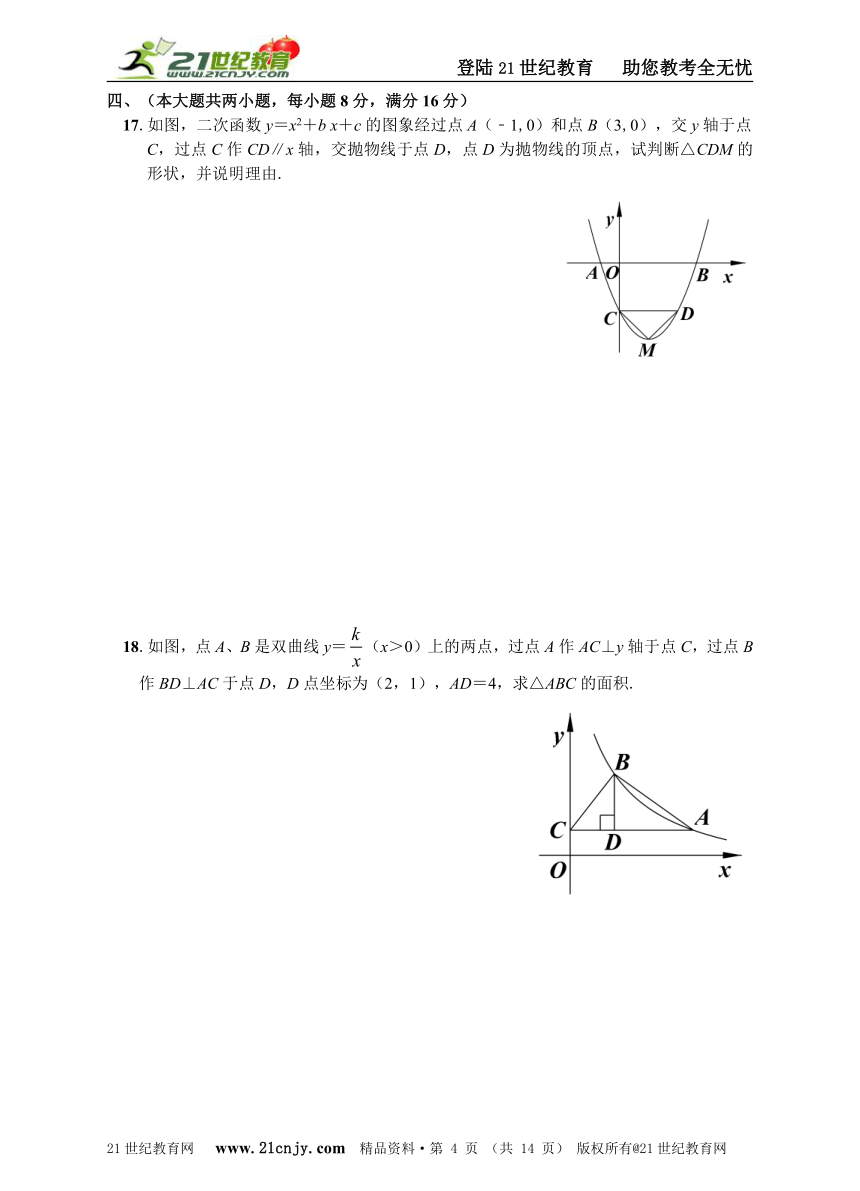
17.如图,二次函数y=x2+b x+c的图象经过点A(﹣1,0)和点B(3,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D,点D为抛物线的顶点,试判断△CDM的形状,并说明理由.21cnjy.com
18.如图,点A、B是双曲线y=(x>0)上的两点,过点A作AC⊥y轴于点C,过点B作BD⊥AC于点D,D点坐标为(2,1),AD=4,求△ABC的面积.
五、(本大题共两小题,每小题10分,满分20分)
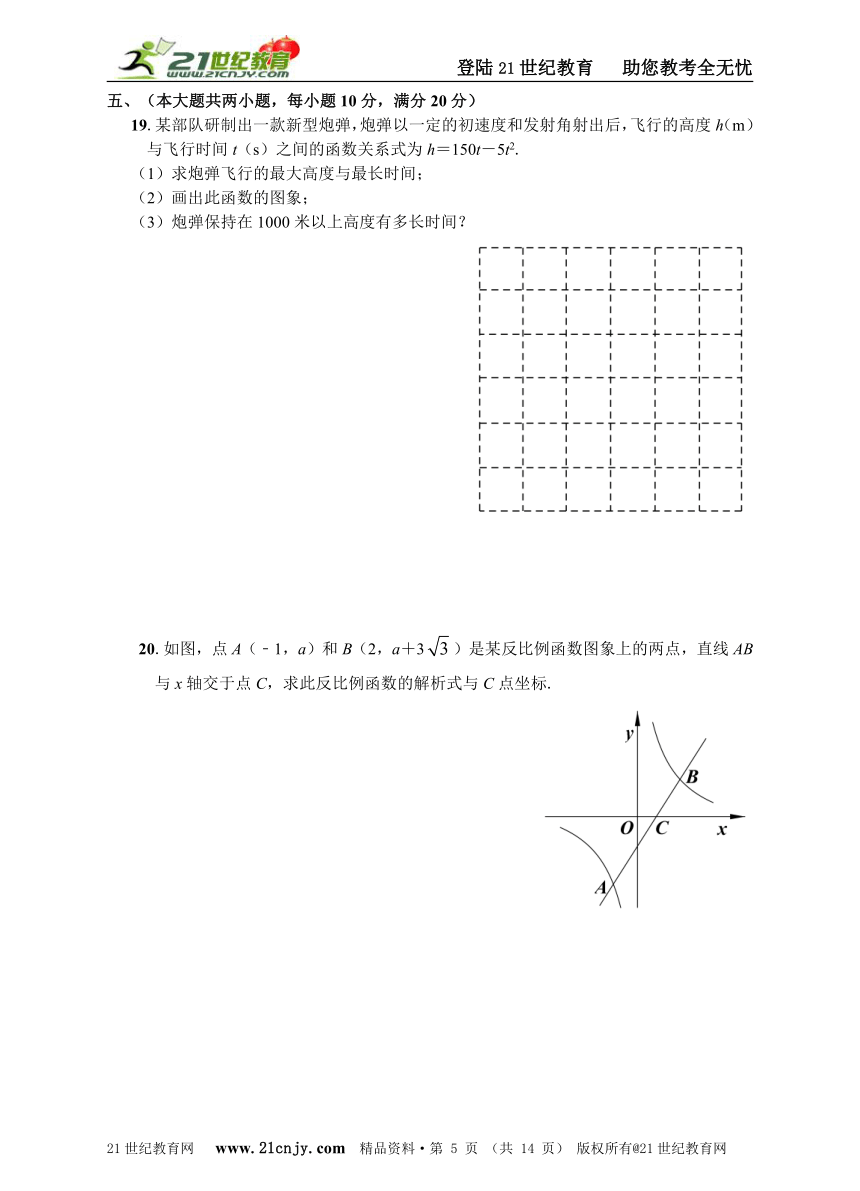
19.某部队研制出一款新型炮弹,炮弹以一定的初速度和发射角射出后,飞行的高度h(m)与飞行时间t(s)之间的函数关系式为h=150t-5t2.21·cn·jy·com
(1)求炮弹飞行的最大高度与最长时间;
(2)画出此函数的图象;
(3)炮弹保持在1000米以上高度有多长时间?
20.如图,点A(﹣1,a)和B(2,a+3)是某反比例函数图象上的两点,直线AB与x轴交于点C,求此反比例函数的解析式与C点坐标.21·世纪*教育网
六、(本题满分12分)
21.如图,李老板在一次打高尔夫球的训练中,从山坡下的O点打出一球向球洞A点飞去,球的飞行路线为抛物线,当球达到最大高度12米时,球运动的水平距离为9米.已知山坡OA与水平方向(x轴)的夹角为30°,点O与球洞A点的距离为8米.
(1)求球的飞行路线所在抛物线的解析式;
(2)判断李老板这一杆能否把球从O点直接打入球洞A点;
(3)试问将球洞A点怎样移动后李老板这一杆恰能把球打入移动后的球洞中.
七、(本题满分12分)
22.某国产品牌电脑公司在暑假期间搞促销活动,规定每台电脑0.6万元,交首付后,每月须支付金额y(元)与时间t(月)的关系如图所示: 21*cnjy*com
(1)求首付款是多少元? 并求出此函数关系式.
(2)若要求每月支付的钱不少于500元,则最多还有几个月才能将所有的钱全部付清?
八、(本题满分14分)
23.我校团总支组织学生会干部利用校园内的一块空地围建一个矩形花园,其中一边靠墙,另三边用30米长的篱笆围成,已知墙长为18米,如图所示.
(1)若围成正方形,求正方形花园的面积;
(2)怎样围才能使花园的面积最大,最大面积是多少?
(3)若围成的花园的面积不超过112平方米,试利用二次函数的有关性质求花园垂直于墙的一边的长度的范围. www.21-cn-jy.com
参考答案
1.B 解析:把点(﹣3,5)代入y=ax2+b x﹣2得9a﹣3b=7,
∴a﹣b=,∴a-b-=-=,∴选B
2. D 解析:∵关于x的一元二次方程x2-x+n=0有两个不相等的实数根,
∴△=(﹣1)2-4n>0,∴4n-1<0,∵﹣=﹣=>0,
==<0,∴此抛物线顶点在第四象限,∴选D
3. A 解析:∵函数y=(a+2)x2-2x+1的图象与x轴有交点,∴△=(﹣2)2-4(a+2)≥0,解得a≤﹣1,又当a+2=0即a=﹣2时,y=﹣2x+1,其图象与x轴有一个交点,∴选A 21世纪教育网版权所有
4.C 解析:设y=ax2+bx+c,将点A,B的坐标代入得c=3,a+b+c=0,∴a+b=﹣3①,又∵﹣=﹣1,∴2a-b=0②,联立①②解得a=﹣1,b=﹣2,∴y=﹣x2-2x+3,∴②对;∵y=﹣x2-2x+3=﹣(x+1)2+4,∴抛物线的顶点坐标为(﹣1,4),∴①对;∵a=﹣1<0,对称轴为直线x=﹣1,∴当x<﹣1时,y随x的增大而增大,∴③错;由y=0得﹣x2-2x+3=0,解得x1=1,x2=﹣3,∴抛物线与x轴另一个交点为(﹣3,0),∴④对.∴选C
5.B 解析:由题意设P=,把点(1.5,50)代入得k=1.5×50=75,∴P=,由题意可知为了安全,应有P≤100,∴≤100,解得V≥,∴选B
6.D 解析:∵抛物线与x轴有两个交点,∴△=b2-4ac>0,①对;∵抛物线的对称轴在点(0,0)和(1,0)之间,∴﹣ <1,又抛物线开口向上,∴a>0,∴﹣b<2a,∴2a-b>0,∴②对;当x=1时,y=a+b+c,观察下图,点(1,a+b+c)在第四象限,∴a+b+c<0,③对;观察下图,当y=﹣1时,对应的x的值一正一负,∴方程ax2+b x+c=﹣1的两根一正一负,∴④错.∴选D
7.D 解析:把点(0,﹣2)代入y=x2+bx+c得c=﹣2,∴y=x2+bx-2,设方程x2+bx-2=0的两根为x1,x2,则x1+x2=﹣b,x1x2,=﹣2,∴x1=﹣,令﹣3<x1<﹣1①,则x1<0,∴x2>0,∴﹣3<﹣<﹣1,解得<x2<2②,①+
②得﹣<x1+x2<1,∴﹣<﹣b<1,解得﹣1<b<,∴选D
8.D 解析:由h=2得﹣s2+s+=2,化简得s2-8s+6=0,解得s1=4+,s2=4-(不合题意,舍去),∴a的取值范围是5<a<4+,∴选D
9.C 解析:由题意得A,B两点坐标分别为(0,1.5),(3,0),把这两点的坐标分别代入y=﹣x2+b x+c得,解得b=1,c=1.5,∴y=﹣x2+x+=﹣(x-1)2+2,当x=1时,y最大=2,∴选C
10.C 解析:如下图,过点C作CE⊥x轴于点E,∵直线OC的解析式为y=x,∴∠CEO=45°,∴△CEO是等腰直角三角形,设CE=OE=m,则OC=m=OA,∵S菱形OABC=2,∴OA×CE=2,∴m·m=2,解得m=,∴OE=,OA=2,又∵D为BC的中点,且BC∥OA,∴点D的坐标为(+1,),设双曲线解析式为y=,把D点坐标代入得k=(+1)=2+,∴双曲线的解析式为y=,∴选C 21教育网
11.答案不唯一,如y=﹣x2+3x-1 解析:设y=ax2+4x+c,∵抛物线与y轴交点的纵坐标为﹣1,∴抛物线过点(0,﹣1),又抛物线过点(2,1),把这两点的坐标代入解析式得c=﹣1,4a+2b+c=1,∴2a+b=1,∵a<0,∴可令a=﹣1,则b=3,∴抛物线的一个解析式为y=﹣x2+3x-1 【来源:21·世纪·教育·网】
12.③ 解析:∵小球在发射后第1秒和第4秒的高度相等,∴抛物线的对称轴为直线t=
=2.5,∵a<0,∴当t=2.5时,h最大,∴t越接近2.5,h越大,∴填③
13.﹣1<x<4 解析:观察图象可知,y1与y2交点的横坐标分别为﹣1和4,当﹣1<x<4时,y1图象位于y2图象的下方(即当﹣1<x<4时,x每取一个值,对应的y1值总小于y2值),∴不等式ax2+bx+c<mx+n的解集为﹣1<x<4
14. y1= 解析:如下图,延长AB交y轴于点C,∵AB∥x轴,∴AB⊥y轴于点C,∵点B在双曲线y2上,y2=,∴S△COB==1.5,又∵S△AOB=1,∴S△AOC=S△COB+S△AOB =1.5+1=2.5,设y1=,∵点A在双曲线y1上,∴ =2.5×2=5,∵k>0,∴k=5,∴y1的关系式为y1=
15.解:设抛物线的解析式为y=a(x+h)2+k,∵其顶点为(﹣2,3),∴h=﹣(﹣2)=2,k=3,∴y=a(x+2)2+3,把点(1,﹣5)代入解析式得a×(1+2)2+3=﹣5,解得a=﹣,∴此抛物线的解析式为y=﹣(x+2)2+3=﹣x2-x-.
16.解:∵二次函数y=﹣x2+(m-1)x+m2的图象经过原点,∴把原点坐标(0,0)代入函数解析式得m2=0,∴m=0,∴把m=0代入解析式得y=﹣x2-x,由配方法得,y=﹣x2-x=-(x+)2+,将此函数图象向左平移个单位,得y=-(x-1)2+,∵a=﹣1<0,∴当x>1时,y随x的增大而减小,当x<1时,y随x的增大而增大,∴将函数y=﹣x2+(m-1)x+m2向左平移个单位,可使得平移后的函数在x>1时,y随x的增大而减小,在x<1时,y随x的增大而增大.
17. 解:△CDM为等腰直角三角形,理由如下:如下图,过点M作MN⊥CD于点N,把
点A(﹣1,0)和B(3,0)的坐标分别代入y=x2+bx+c得,解得b=﹣2,c=﹣3,∴y=x2﹣2x﹣3=(x-1)2-4,∴C(0,﹣3),M(1,﹣4),∵CD∥x轴,∴由抛物线的对称性得D(2,﹣3),CD=2,∴CM=DM=1,∴△CDM是等腰三角形,又MN=4-3=1,∴CN=DN=MN,∴△CNM、△DNM均为等腰直角三角形,∴△CDM为等腰直角三角形 www-2-1-cnjy-com
18.解:∵D(2,1),∴CD=2,CO=1,∵AD=4,∴AC=AD+CD=4+2=6,∵AC⊥y轴,∴A(6,1),把点A的坐标代入y=得k=6×1=6,∴y=,当x=2时,y==3,∵BD⊥AC,∴B(2,3),∴BD=3-1=2,∴S△ABC=×AC×BD=×6×2=6.【来源:21cnj*y.co*m】
19. 解:(1)h=150t-5t2=﹣5(t-15)2+1125,当t=15时,h最大=1125,∴炮弹飞行的最大高度为1125米;由h=0得150t-5t2=0,解得t1=0,t2=30,∴炮弹飞行的最长时间为30秒;【出处:21教育名师】
(2)画出此函数的图象如下图:
(3)当h=1000时,可得﹣5(t-15)2+1125=1000,解得t1=10,t2=20,t2-t1=20-10=10(s),∴炮弹保持在1000米以上高度的时间有10s.
20.解:设此反比例函数的解析式为y=,把点A(﹣1,a)和B(2,a+3)坐标分别代入得k=﹣a=2(a+3),解得a=﹣2,∴k=2,∴此反比例函数的解析式为y=,∴A(﹣1,﹣2),B(2,),设直线AB的解析式为y=kx+b,把A,B两点的坐标分别代入得,解得k=,b=﹣,∴直线AB的解析式为y=x﹣,当y=0时,x﹣=0,解得x=1,∴点C的坐标为(1,0).【版权所有:21教育】
21.解:(1)设抛物线的解析式为y=a(x+h)2+k,如下图,由题意知抛物线顶点C的坐标为(9,12),∴h=﹣9,k=12,∴y=a(x﹣9)2+12,把点O(0,0)坐标代入得a=﹣,∴y=﹣(x﹣9)2+12=﹣x2+x;
(2)不能,理由如下:如下图,过点A作AB⊥x轴于点B,则∠AOB=30°,OA=8,∴AB=OA=4,由勾股定理得OB===12,∴A点坐标为(12,4),当x=12时,y=﹣×122+×12=≠4,∴A点不在抛物线上,∴李老板这一杆不能把球从O点直接打入球洞A点;2·1·c·n·j·y
(3)设直线OA的解析式为y=kx,把点A(12,4)坐标代入得k=,∴y=x,由题意得﹣x2+x=x,解得x=,-12=,∴将球洞A点沿山坡向上移动,且移动的水平距离为米时,李老板这一杆恰能把球打入移动后的球洞中.21教育名师原创作品
22.解:(1)首付款为0.6万元-400元×10=2000元;由题意及图象可知此函数为反比例函数,设y=,把点(10,400)代入得k=4000,∴y=;
(2)由题意得y≥500,又y=,∴≥500,解得t≤8,∴最多还有8个月才能将所有的钱全部付清.21*cnjy*com
23.解:(1)=(m),10×10=100(m2).
答:若围成正方形花园,则正方形花园的面积为100m2;
(2)设花园垂直于墙的一边的长为xm,花园的面积为y m2,由题意得y=x(30-2x)=﹣2x2+30x=﹣2(x-7.5)2+112.5,∵﹣2<0,∴当x=7.5时,y最大=112.5,30-2x=30-2×7.5=15(m).
答:花园垂直于墙的一边长为7.5m,平行于墙的一边长为15m时,花园面积最大,最大面积为112.5 m2.
当y=112时,﹣2(x-7.5)2+112.5=112,解得x1=7,x2=8.
∵﹣2<0,∴当x<7.5时,y随x的增大而增大,当x>7.5时,y随x的增大而减小,
∴当6≤x≤7或8≤x<15时,y的值不超过112.
答:若围成的花园的面积不超过112平方米,花园垂直于墙的一边x的长度的范围是6≤x≤7或8≤x<15.
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.抛物线y=ax2+b x﹣2经过点(﹣3,5),则a-b-的值为……………………【 】
A. B. C. D.
2.关于x的一元二次方程x2-x+n=0有两个不相等的实数根,则抛物线y=x2-x+n的顶点一定在……………………………………………………………………………【 】
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知函数y=(a+2)x2-2x+1的图象与x轴有交点,则a的取值范围是…………【 】
A.a≤﹣1 B. a≤﹣1且a≠﹣2 C. a<﹣1 D. a<﹣1且a≠﹣2
4.如图,某函数的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是直线x=﹣1,则下列结论:①抛物线的顶点坐标为(﹣1,4);②此函数的解析式为y=﹣x2-2x+3;③当x<0时,y随x的增大而增大;④抛物线与x轴的另一个交点是(﹣3,0).其中正确的有………………………………………………………………【 】
A.①② B.①②③ C.①②④ D.②③④
5.某种气球内充满一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V(m3)的反比例函数,其图象如图,当气球内的气压大于100 kPa时,气球将爆炸,为了安全,气球的体积应满足的条件是………………………………………【 】
A.不大于m3 B. 不小于m3 C. 大于m3 D. 小于m3
6.如图,是二次函数y=ax2+bx+c的图象,小元同学认真观察图象,获得如下四条信息:①b2-4ac>0;②2a+b>0;③a+b+c<0;④当y=﹣1时,方程ax2+b x+c=﹣1的两根均为正数.其中不正确的是………………………………………………【 】
A.① B.② C.③ D.④
7.已知抛物线y=x2+bx+c经过点(0,﹣2),若要使该抛物线与x轴的一个交点在(﹣3,0)和(﹣1,0)之间,则抛物线的解析式不可能是……………………………【 】
A. y=x2-2 B. y=x2+x-2 C. y=x2+2x-2 D. y=x2+3x-2
8.甲、乙两人进行羽毛球比赛,最后关头,甲发出一个十分关键的球,球的出手点为M,球距地面高度h(m)与其飞出的水平距离s(m)之间的关系式为h=﹣s2+s+,如图所示,已知球网AB距原点5m,乙(用线段EF表示)扣球的最大高度为2m,设乙的起跳点E的横坐标为a,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则a的取值范围是………………………………………………【 】
A.a>5 B.5<a<6 C. 5<a<4+ D. 5<a<4+
9.在今年的六一儿童节期间,我校举行了七、八年级“庆六一”篮球友谊赛.如图是我班阿文同学某次投球时的篮球运动路线图,可以看做是抛物线y=﹣x2+b x+c的一部分,其中出球点A离地面O点的距离为1.5m,篮球落地点B离O点的距离是3m,则此次投球中篮球达到的最大高度是………………………………………………【 】
A.1m B. 2m C. 3m D. 4m
10.如图,四边形OABC是菱形,点A在x轴上,直线y=x经过点C,菱形OABC的面积为2,过BC中点D的双曲线的解析式为……………………………………【 】
A. y= B. y= C. y= D. y=
二、填空题(本大题共4小题,每小题5分,满分20分)
11.请写出一个开口向下,与y轴交点的纵坐标为﹣1,且经过点(2,1)的抛物线的解析式为___________________________.2-1-c-n-j-y
12.竖直向上发射的小球的高度h(m)与运动时间t(s)的函数关系式为h=at2+bt,其图象如图所示,若小球在发射后第1秒和第4秒的高度相等,则下列时刻:①第1.5秒;②第2.2秒;③第2.6秒;④第3秒.其中小球的高度最高的是___________(把你认为正确的时刻的序号填在横线上).
13.如图,是二次函数y1=ax2+bx+c与一次函数y2=mx+n的图象,观察图象可得不等式ax2+bx+c<mx+n的解集为_______________.
14.如图,双曲线y1、y2各一部分在第一象限,点A在双曲线y1上,点B在双曲线y2上,AB∥x轴,若S△AOB=1,y2=,则y1的关系式为____________.
三、(本大题共两小题,每小题8分,满分16分)
15.已知抛物线的顶点为(﹣2,3),且经过点(1,﹣5),求这个抛物线的解析式.
16.二次函数y=﹣x2+(m-1)x+m2的图象经过原点,通过怎样的平移,可使得平移后的函数在x>1时,y随x的增大而减小,在x<1时,y随x的增大而增大?
四、(本大题共两小题,每小题8分,满分16分)
17.如图,二次函数y=x2+b x+c的图象经过点A(﹣1,0)和点B(3,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D,点D为抛物线的顶点,试判断△CDM的形状,并说明理由.21cnjy.com
18.如图,点A、B是双曲线y=(x>0)上的两点,过点A作AC⊥y轴于点C,过点B作BD⊥AC于点D,D点坐标为(2,1),AD=4,求△ABC的面积.
五、(本大题共两小题,每小题10分,满分20分)
19.某部队研制出一款新型炮弹,炮弹以一定的初速度和发射角射出后,飞行的高度h(m)与飞行时间t(s)之间的函数关系式为h=150t-5t2.21·cn·jy·com
(1)求炮弹飞行的最大高度与最长时间;
(2)画出此函数的图象;
(3)炮弹保持在1000米以上高度有多长时间?
20.如图,点A(﹣1,a)和B(2,a+3)是某反比例函数图象上的两点,直线AB与x轴交于点C,求此反比例函数的解析式与C点坐标.21·世纪*教育网
六、(本题满分12分)
21.如图,李老板在一次打高尔夫球的训练中,从山坡下的O点打出一球向球洞A点飞去,球的飞行路线为抛物线,当球达到最大高度12米时,球运动的水平距离为9米.已知山坡OA与水平方向(x轴)的夹角为30°,点O与球洞A点的距离为8米.
(1)求球的飞行路线所在抛物线的解析式;
(2)判断李老板这一杆能否把球从O点直接打入球洞A点;
(3)试问将球洞A点怎样移动后李老板这一杆恰能把球打入移动后的球洞中.
七、(本题满分12分)
22.某国产品牌电脑公司在暑假期间搞促销活动,规定每台电脑0.6万元,交首付后,每月须支付金额y(元)与时间t(月)的关系如图所示: 21*cnjy*com
(1)求首付款是多少元? 并求出此函数关系式.
(2)若要求每月支付的钱不少于500元,则最多还有几个月才能将所有的钱全部付清?
八、(本题满分14分)
23.我校团总支组织学生会干部利用校园内的一块空地围建一个矩形花园,其中一边靠墙,另三边用30米长的篱笆围成,已知墙长为18米,如图所示.
(1)若围成正方形,求正方形花园的面积;
(2)怎样围才能使花园的面积最大,最大面积是多少?
(3)若围成的花园的面积不超过112平方米,试利用二次函数的有关性质求花园垂直于墙的一边的长度的范围. www.21-cn-jy.com
参考答案
1.B 解析:把点(﹣3,5)代入y=ax2+b x﹣2得9a﹣3b=7,
∴a﹣b=,∴a-b-=-=,∴选B
2. D 解析:∵关于x的一元二次方程x2-x+n=0有两个不相等的实数根,
∴△=(﹣1)2-4n>0,∴4n-1<0,∵﹣=﹣=>0,
==<0,∴此抛物线顶点在第四象限,∴选D
3. A 解析:∵函数y=(a+2)x2-2x+1的图象与x轴有交点,∴△=(﹣2)2-4(a+2)≥0,解得a≤﹣1,又当a+2=0即a=﹣2时,y=﹣2x+1,其图象与x轴有一个交点,∴选A 21世纪教育网版权所有
4.C 解析:设y=ax2+bx+c,将点A,B的坐标代入得c=3,a+b+c=0,∴a+b=﹣3①,又∵﹣=﹣1,∴2a-b=0②,联立①②解得a=﹣1,b=﹣2,∴y=﹣x2-2x+3,∴②对;∵y=﹣x2-2x+3=﹣(x+1)2+4,∴抛物线的顶点坐标为(﹣1,4),∴①对;∵a=﹣1<0,对称轴为直线x=﹣1,∴当x<﹣1时,y随x的增大而增大,∴③错;由y=0得﹣x2-2x+3=0,解得x1=1,x2=﹣3,∴抛物线与x轴另一个交点为(﹣3,0),∴④对.∴选C
5.B 解析:由题意设P=,把点(1.5,50)代入得k=1.5×50=75,∴P=,由题意可知为了安全,应有P≤100,∴≤100,解得V≥,∴选B
6.D 解析:∵抛物线与x轴有两个交点,∴△=b2-4ac>0,①对;∵抛物线的对称轴在点(0,0)和(1,0)之间,∴﹣ <1,又抛物线开口向上,∴a>0,∴﹣b<2a,∴2a-b>0,∴②对;当x=1时,y=a+b+c,观察下图,点(1,a+b+c)在第四象限,∴a+b+c<0,③对;观察下图,当y=﹣1时,对应的x的值一正一负,∴方程ax2+b x+c=﹣1的两根一正一负,∴④错.∴选D
7.D 解析:把点(0,﹣2)代入y=x2+bx+c得c=﹣2,∴y=x2+bx-2,设方程x2+bx-2=0的两根为x1,x2,则x1+x2=﹣b,x1x2,=﹣2,∴x1=﹣,令﹣3<x1<﹣1①,则x1<0,∴x2>0,∴﹣3<﹣<﹣1,解得<x2<2②,①+
②得﹣<x1+x2<1,∴﹣<﹣b<1,解得﹣1<b<,∴选D
8.D 解析:由h=2得﹣s2+s+=2,化简得s2-8s+6=0,解得s1=4+,s2=4-(不合题意,舍去),∴a的取值范围是5<a<4+,∴选D
9.C 解析:由题意得A,B两点坐标分别为(0,1.5),(3,0),把这两点的坐标分别代入y=﹣x2+b x+c得,解得b=1,c=1.5,∴y=﹣x2+x+=﹣(x-1)2+2,当x=1时,y最大=2,∴选C
10.C 解析:如下图,过点C作CE⊥x轴于点E,∵直线OC的解析式为y=x,∴∠CEO=45°,∴△CEO是等腰直角三角形,设CE=OE=m,则OC=m=OA,∵S菱形OABC=2,∴OA×CE=2,∴m·m=2,解得m=,∴OE=,OA=2,又∵D为BC的中点,且BC∥OA,∴点D的坐标为(+1,),设双曲线解析式为y=,把D点坐标代入得k=(+1)=2+,∴双曲线的解析式为y=,∴选C 21教育网
11.答案不唯一,如y=﹣x2+3x-1 解析:设y=ax2+4x+c,∵抛物线与y轴交点的纵坐标为﹣1,∴抛物线过点(0,﹣1),又抛物线过点(2,1),把这两点的坐标代入解析式得c=﹣1,4a+2b+c=1,∴2a+b=1,∵a<0,∴可令a=﹣1,则b=3,∴抛物线的一个解析式为y=﹣x2+3x-1 【来源:21·世纪·教育·网】
12.③ 解析:∵小球在发射后第1秒和第4秒的高度相等,∴抛物线的对称轴为直线t=
=2.5,∵a<0,∴当t=2.5时,h最大,∴t越接近2.5,h越大,∴填③
13.﹣1<x<4 解析:观察图象可知,y1与y2交点的横坐标分别为﹣1和4,当﹣1<x<4时,y1图象位于y2图象的下方(即当﹣1<x<4时,x每取一个值,对应的y1值总小于y2值),∴不等式ax2+bx+c<mx+n的解集为﹣1<x<4
14. y1= 解析:如下图,延长AB交y轴于点C,∵AB∥x轴,∴AB⊥y轴于点C,∵点B在双曲线y2上,y2=,∴S△COB==1.5,又∵S△AOB=1,∴S△AOC=S△COB+S△AOB =1.5+1=2.5,设y1=,∵点A在双曲线y1上,∴ =2.5×2=5,∵k>0,∴k=5,∴y1的关系式为y1=
15.解:设抛物线的解析式为y=a(x+h)2+k,∵其顶点为(﹣2,3),∴h=﹣(﹣2)=2,k=3,∴y=a(x+2)2+3,把点(1,﹣5)代入解析式得a×(1+2)2+3=﹣5,解得a=﹣,∴此抛物线的解析式为y=﹣(x+2)2+3=﹣x2-x-.
16.解:∵二次函数y=﹣x2+(m-1)x+m2的图象经过原点,∴把原点坐标(0,0)代入函数解析式得m2=0,∴m=0,∴把m=0代入解析式得y=﹣x2-x,由配方法得,y=﹣x2-x=-(x+)2+,将此函数图象向左平移个单位,得y=-(x-1)2+,∵a=﹣1<0,∴当x>1时,y随x的增大而减小,当x<1时,y随x的增大而增大,∴将函数y=﹣x2+(m-1)x+m2向左平移个单位,可使得平移后的函数在x>1时,y随x的增大而减小,在x<1时,y随x的增大而增大.
17. 解:△CDM为等腰直角三角形,理由如下:如下图,过点M作MN⊥CD于点N,把
点A(﹣1,0)和B(3,0)的坐标分别代入y=x2+bx+c得,解得b=﹣2,c=﹣3,∴y=x2﹣2x﹣3=(x-1)2-4,∴C(0,﹣3),M(1,﹣4),∵CD∥x轴,∴由抛物线的对称性得D(2,﹣3),CD=2,∴CM=DM=1,∴△CDM是等腰三角形,又MN=4-3=1,∴CN=DN=MN,∴△CNM、△DNM均为等腰直角三角形,∴△CDM为等腰直角三角形 www-2-1-cnjy-com
18.解:∵D(2,1),∴CD=2,CO=1,∵AD=4,∴AC=AD+CD=4+2=6,∵AC⊥y轴,∴A(6,1),把点A的坐标代入y=得k=6×1=6,∴y=,当x=2时,y==3,∵BD⊥AC,∴B(2,3),∴BD=3-1=2,∴S△ABC=×AC×BD=×6×2=6.【来源:21cnj*y.co*m】
19. 解:(1)h=150t-5t2=﹣5(t-15)2+1125,当t=15时,h最大=1125,∴炮弹飞行的最大高度为1125米;由h=0得150t-5t2=0,解得t1=0,t2=30,∴炮弹飞行的最长时间为30秒;【出处:21教育名师】
(2)画出此函数的图象如下图:
(3)当h=1000时,可得﹣5(t-15)2+1125=1000,解得t1=10,t2=20,t2-t1=20-10=10(s),∴炮弹保持在1000米以上高度的时间有10s.
20.解:设此反比例函数的解析式为y=,把点A(﹣1,a)和B(2,a+3)坐标分别代入得k=﹣a=2(a+3),解得a=﹣2,∴k=2,∴此反比例函数的解析式为y=,∴A(﹣1,﹣2),B(2,),设直线AB的解析式为y=kx+b,把A,B两点的坐标分别代入得,解得k=,b=﹣,∴直线AB的解析式为y=x﹣,当y=0时,x﹣=0,解得x=1,∴点C的坐标为(1,0).【版权所有:21教育】
21.解:(1)设抛物线的解析式为y=a(x+h)2+k,如下图,由题意知抛物线顶点C的坐标为(9,12),∴h=﹣9,k=12,∴y=a(x﹣9)2+12,把点O(0,0)坐标代入得a=﹣,∴y=﹣(x﹣9)2+12=﹣x2+x;
(2)不能,理由如下:如下图,过点A作AB⊥x轴于点B,则∠AOB=30°,OA=8,∴AB=OA=4,由勾股定理得OB===12,∴A点坐标为(12,4),当x=12时,y=﹣×122+×12=≠4,∴A点不在抛物线上,∴李老板这一杆不能把球从O点直接打入球洞A点;2·1·c·n·j·y
(3)设直线OA的解析式为y=kx,把点A(12,4)坐标代入得k=,∴y=x,由题意得﹣x2+x=x,解得x=,-12=,∴将球洞A点沿山坡向上移动,且移动的水平距离为米时,李老板这一杆恰能把球打入移动后的球洞中.21教育名师原创作品
22.解:(1)首付款为0.6万元-400元×10=2000元;由题意及图象可知此函数为反比例函数,设y=,把点(10,400)代入得k=4000,∴y=;
(2)由题意得y≥500,又y=,∴≥500,解得t≤8,∴最多还有8个月才能将所有的钱全部付清.21*cnjy*com
23.解:(1)=(m),10×10=100(m2).
答:若围成正方形花园,则正方形花园的面积为100m2;
(2)设花园垂直于墙的一边的长为xm,花园的面积为y m2,由题意得y=x(30-2x)=﹣2x2+30x=﹣2(x-7.5)2+112.5,∵﹣2<0,∴当x=7.5时,y最大=112.5,30-2x=30-2×7.5=15(m).
答:花园垂直于墙的一边长为7.5m,平行于墙的一边长为15m时,花园面积最大,最大面积为112.5 m2.
当y=112时,﹣2(x-7.5)2+112.5=112,解得x1=7,x2=8.
∵﹣2<0,∴当x<7.5时,y随x的增大而增大,当x>7.5时,y随x的增大而减小,
∴当6≤x≤7或8≤x<15时,y的值不超过112.
答:若围成的花园的面积不超过112平方米,花园垂直于墙的一边x的长度的范围是6≤x≤7或8≤x<15.
