2015沪科版九年级上册数学单元梯度检测精品卷:(三)第21章二次函数与反比例函数单元梯度检测C卷
文档属性
| 名称 | 2015沪科版九年级上册数学单元梯度检测精品卷:(三)第21章二次函数与反比例函数单元梯度检测C卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 355.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-22 00:00:00 | ||
图片预览



文档简介
第21章二次函数与反比例函数单元梯度检测C卷
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.已知函数y=(m2-2m)是关于x的二次函数,m为常数,则一次函数y=mx+m的图象一定不经过点……………………………………………………………【 】
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.关于x的二次函数y=x2在﹣1≤x≤3时的最值情况,以下说法正确的是…………【 】
A.最小值为1,最大值为9 B. 最小值为0,最大值为9
C. 最小值为1,没有最大值 D. 最小值为0,没有最大值
3.已知二次函数y=2(x-1)2+k的图象经过点A(,y1),B(2,y2),C(1-,y3)三点,则y1,y2,y3的大小关系是……………………………………………【 】
A. y1>y2>y3 B. y1>y3>y2 C. y3>y1>y2 D. y3>y2>y1
4.如图,二次函数y=ax2-4x+c的图象与y轴交于点A,且经过点B,点M,N也在此函数图象上,且点M,N关于此抛物线的对称轴对称,点M的坐标为(m, ﹣2m)(m<0),则点N到x轴的距离为…………………………………………………………【 】
A.2 B.4 C.6 D.8
5.如图,在□ABCD中,AB=2,D点坐标为(0,4),以点C为顶点的抛物线y=ax2+bx+c经过x轴上的点A,B,若将抛物线向上平移后恰好经过点D,则平移后的抛物线解析式为…………………………………………………………………………【 】
A. y=﹣4x2+16x-4 B. y=﹣4x2+16x+4
C. y=﹣4x2-16x+4 D. y=﹣4x2-16x-4
6.函数y=x2-x+m的图象如图所示,当x=a时,y<0,求当x=a-1时,y的值.我班五位同学在探究此题时各得到一条相关信息,甲:当x=0时,y=m>0;乙:抛物线的对称轴为直线x=;丙:x1<a<x2;丁:关键要判断a-1的符号;戊:m可以取一个特殊值.请参考这五位同学获得的信息,你的答案是………………………【 】
A. y<0 B.0<y<m C.y>m D.y=m
7.已知抛物线y=ax2+bx+c经过A(0,1)和B(2,﹣3)两点,且开口方向向下,若抛物线的对称轴在y轴右侧,则a的取值范围是…………………………………【 】
A. a<0 B. a<﹣1 C. ﹣1<a<0 D. a<﹣2
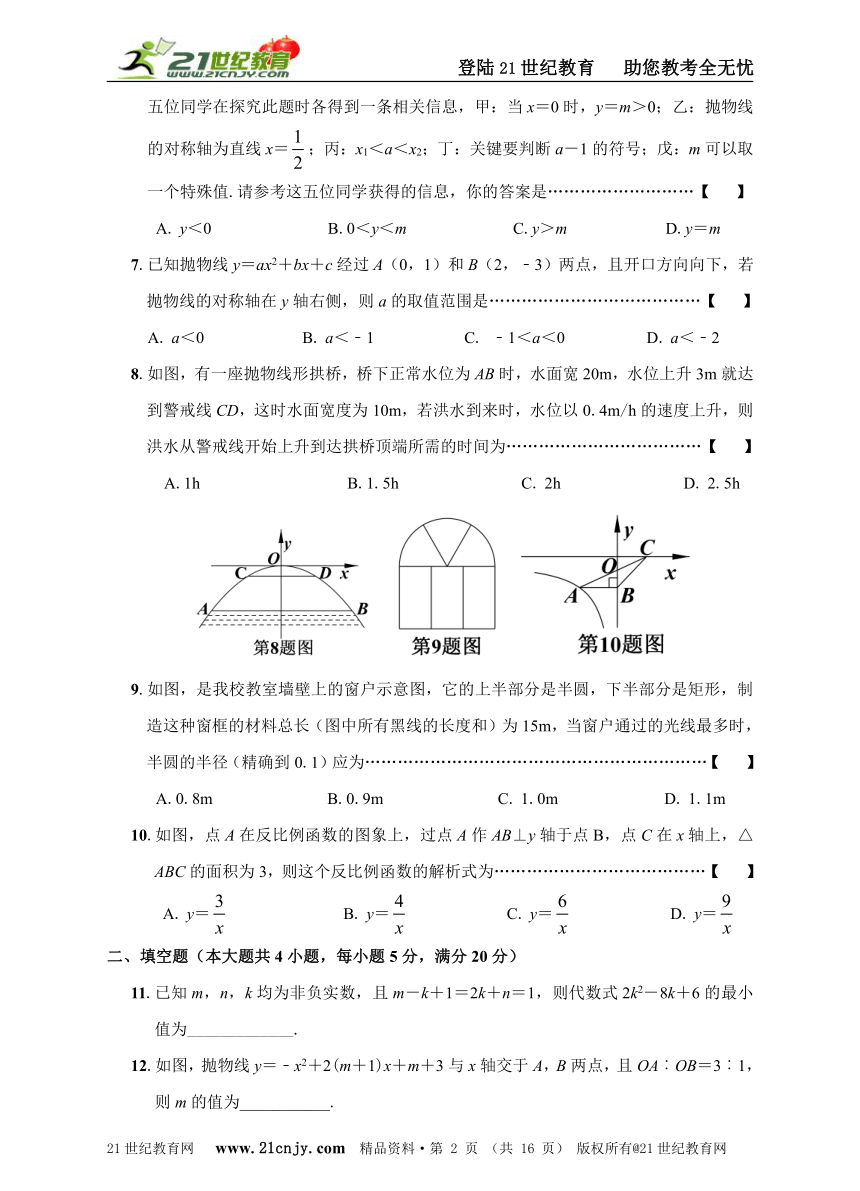
8.如图,有一座抛物线形拱桥,桥下正常水位为AB时,水面宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m,若洪水到来时,水位以0.4m/h的速度上升,则洪水从警戒线开始上升到达拱桥顶端所需的时间为………………………………【 】
A.1h B.1.5h C. 2h D. 2.5h
9.如图,是我校教室墙壁上的窗户示意图,它的上半部分是半圆,下半部分是矩形,制造这种窗框的材料总长(图中所有黑线的长度和)为15m,当窗户通过的光线最多时,半圆的半径(精确到0.1)应为………………………………………………………【 】
A.0.8m B.0.9m C. 1.0m D. 1.1m
10.如图,点A在反比例函数的图象上,过点A作AB⊥y轴于点B,点C在x轴上,△ABC的面积为3,则这个反比例函数的解析式为…………………………………【 】
A. y= B. y= C. y= D. y=
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知m,n,k均为非负实数,且m-k+1=2k+n=1,则代数式2k2-8k+6的最小值为_____________.21·cn·jy·com
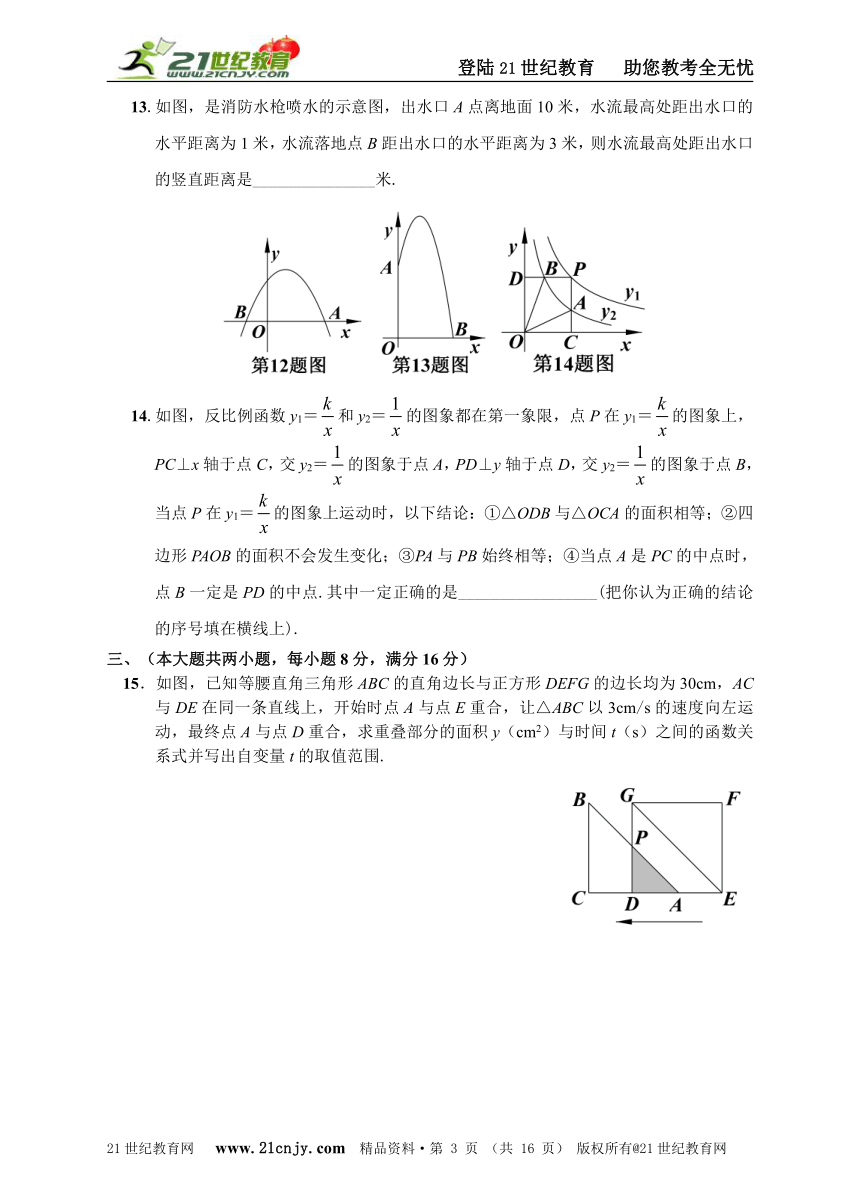
12.如图,抛物线y=﹣x2+2(m+1)x+m+3与x轴交于A,B两点,且OA︰OB=3︰1,则m的值为___________.www.21-cn-jy.com
13.如图,是消防水枪喷水的示意图,出水口A点离地面10米,水流最高处距出水口的水平距离为1米,水流落地点B距出水口的水平距离为3米,则水流最高处距出水口的竖直距离是_______________米.
14.如图,反比例函数y1=和y2=的图象都在第一象限,点P在y1=的图象上,PC⊥x轴于点C,交y2=的图象于点A,PD⊥y轴于点D,交y2=的图象于点B,当点P在y1=的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是_________________(把你认为正确的结论的序号填在横线上).
三、(本大题共两小题,每小题8分,满分16分)
15.如图,已知等腰直角三角形ABC的直角边长与正方形DEFG的边长均为30cm,AC与DE在同一条直线上,开始时点A与点E重合,让△ABC以3cm/s的速度向左运动,最终点A与点D重合,求重叠部分的面积y(cm2)与时间t(s)之间的函数关系式并写出自变量t的取值范围.
16.已知二次函数的图象经过点A(﹣1,0)和点B(2,﹣1),其对称轴是直线x=1,求这个二次函数的解析式. 21*cnjy*com
四、(本大题共两小题,每小题8分,满分16分)
17.已知抛物线y=a(x-3)2-6经过点(5,﹣2).
(1)求抛物线的解析式;
(2)若点M(m,y1)和点N(n, y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
18.解师傅想利用一种不锈钢条为边加工一个面积为1.2m2的矩形模具,设模具的长为ym,宽为xm.
(1)请写出y与x的函数关系式,y与x是什么函数关系?
(2)要使模具的长比宽多2.6m,已知这种不锈钢条每米6.5元,试求加工这个模具共需多少钱?
五、(本大题共两小题,每小题10分,满分20分)
19.已知抛物线y=ax2+bx-2经过A(﹣1,0)、B(1,﹣2)两点,直线l1:y=2x-5.21世纪教育网版权所有
(1)求抛物线的解析式;
(2)求证:抛物线与直线l1没有公共点;
(3)若与直线l1平行的直线l2:y=2x-m2与抛物线只有一个公共点,求这个公共点的坐标.
20.某小内有一块长50m、宽40m的空地,现要将其建成广场,设计图案如图,阴影区域为绿化区(四块绿化区是全等矩形),空白区域是活动区,且四周出口一样宽,宽度不小于25m,不大于30m,预计活动区造价30元/平方米,绿化区造价25元/平方米.2·1·c·n·j·y
(1)设绿化区矩形较长的边长为xm,试写出工程总造价y(元)与x的函数关系式,并写出自变量的取值范围;www-2-1-cnjy-com
(2)请你设计一种投资最小的方案,并求出最小投资.
六、(本题满分12分)
21.如图,一次函数y=﹣x+2分别交x轴、y轴于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点.21·世纪*教育网
(1)求这个抛物线的解析式;
(2)作垂直于x轴的直线x=n,在第一象限交直线AB于点C,交这个抛物线于点D,求当n取何值时,CD有最大值?最大值是多少? 【来源:21·世纪·教育·网】
(3)在(2)的条件下,以B,C,D,E为顶点作平行四边形,试求第四个顶点E的坐标.
七、(本题满分12分)
22.当前,广场舞风靡全球,某服装超市从中发现商机,决定销售一款超短裙.已知每件超短裙的进价为40元,每年销售该款超短裙的总开支(不含进价)共计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在如图所示的一次函数关系. 21*cnjy*com
(1)求y与x的函数关系式;
(2)试写出该超市销售该款超短裙的年获利z(万元)与销售单价x(元)的函数关系式(年获利=年销售额-年总进价-年总开支).当超市希望该款超短裙年获利不低于40万元,试画出函数图象,并帮该超市确定销售单价的范围.在此情况下,要使该款超短裙销量最大,你认为销售单价应定为多少元?
八、(本题满分14分)
23.如图,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在反比例函数y=(k>0,x>0)的图象上,点P(m,n)是反比例函数y=(k>0,x>0)的图象上任意一点,过点P分别作PE⊥x轴于点E,PF⊥y轴于点F,设矩形OEPF与正方形OABC不重合部分的面积为S.
(1)求B点坐标和反比例函数的解析式;
(2)当S=时,求点P的坐标;
(3)写出S关于m的函数关系式.
参考答案
1.A 解析:由题意得,解得m=﹣1,∴一次函数解析式为y=﹣x-1,它的图象经过第二、三、四象限,∴选A. 2-1-c-n-j-y
2. B 解析:当﹣1≤x<0时,0<y≤1;当x=0时,y=0,;当0<x≤3时,0<y≤9.∴综
上,当﹣1≤x≤3时,y最小=0,y最大=9,∴选B.
3.C解析:画出函数的大致图象,如下图,∵2>0,∴图象上距离对称轴越近的点,其纵坐标越小,∵-1<1.3,2-1=1,+1=>1.7,∴>-1>1,∴B点距离对称轴最近,C点距离对称轴最远,∴y3>y1>y2,∴选C.(本题也可用代入法:把A,B,C三点的横坐标代入,计算后再比较大小)
4.A 解析:把点A(0,﹣3),B(3,﹣7)代入y=ax2-4x+c得,解得a=1,c=﹣3,∴y=x2-4x-3,其对称轴为直线x=﹣=1,把点M(m, ﹣2m)代入得m2-4m-3=﹣2m,解得m1=﹣1,m2=3,∵m<0,∴m=﹣1,∴M(﹣1, 2),∵点M,N关于此抛物线的对称轴对称,∴N(3,2),∴点N到x轴的距离为2,∴选A. 【来源:21cnj*y.co*m】
5.B 解析:∵AB=CD=2,AB∥CD,D(0,4),∴C(2,4),
如下图,设抛物线对称轴与x轴交于点H,
由抛物线的对称轴可得H为AB的中点,
∴AH=1,又DC=OH=2,∴OA=1,∴A(1,0),
设抛物线解析式为y=a(x-2)2+4,把A(1,0)代入得a=﹣4,
∴y=﹣4 (x-2)2+4,
设向上平移后的抛物线解析式为y=﹣4 (x-2)2+4+k,把D(0,4)代入解得k=16,
∴向上平移后的抛物线解析式为y=﹣4 (x-2)2+4+16=﹣4x2+16x+4.
6.C 解析:∵抛物线的对称轴为x=,∴<x2<1,又x1<a<x2,∴a<1,∴a-1<0,∵x=0时,y=m,∴观察图象可得当x=a-1时,y>m,∴选C.
7.B 解析:∵抛物线开口向下,∴a<0,又∵抛物线对称轴在y轴右侧,∴﹣>0,∴b>0,把点(0,1)和(2,﹣3)代入y=ax2+bx+c得,∴2a+b=﹣2,∴b=﹣2-2a,∴﹣2-2a>0,解得a<﹣1,解不等式得a<﹣1,∴选B 21cnjy.com
8.D 解析:设拱桥所在抛物线的解析式为y=ax2,由题意设D点坐标为(5,n),则B点坐标为(10,n-3),将B,D两点坐标代入解析式得,解得,∴洪水从警戒线开始上升到达拱桥顶端所需的时间为==2.5(h),∴选D. 【出处:21教育名师】
9.D 解析:设半圆的半径为xm,小矩形的竖直边长为ym,由题意得y=,设窗户的面积为S,则S=x2+2xy=x2+2x×=﹣3.5 x2+7.5x ,∵﹣3.5<0,∴当x=﹣≈1.1时,S最大=≈4.0,∴选D. 【版权所有:21教育】
10.C 解析:如下图,连接OA,∵AB∥x轴,∴S△OAB=S△ABC=3,设反比例函数解析式为y=,由反比例函数的性质可得S△OAB=,∴=6,∵函数图象在第三象限,∴k>0,∴k=6,∴y=,∴选C .21教育名师原创作品
11.2.5 解析:∵m,n,k均为非负实数,∴m,n,k的最小值均为0,又∵2k+n=1,∴当n最小为0时,k最大为,∴0≤k≤,∵2k2-8k+6=2(k-2)2-2,∴当k≤2时,代数式2k2-8k+6的值随k的增大而减小,∴当k=时,代数式2k2-8k+6取得最小值,为2×()2-8×+6=2.5.
12.0 解析:设A(x1,0),B(x2,0),∵OA︰OB=3︰1,∴x2=﹣3x1,观察图象得抛物线
与x轴有两个交点,∴方程﹣x2+2(m+1)x+m+3=0有两个不相等的实数根,
由韦达定理得x1+x2=2(m+1),x1x2=﹣(m+3),把x2=﹣3x1分别代入得
,消去x1得3(m+1)2=m+3,解得m1=0,m2=﹣,观察
图象得x1<0,x2>0,<,∴x1+x2>0,当m=﹣时,x1+x2=﹣<
0,∴m=﹣不合题意,舍去,∴m=0.
13. 解析:由题意知抛物线顶点横坐标为1,∴可设抛物线解析式为y=a(x-1)2+k,
由题意知抛物线经过点A(0,10)、B(3,0),把这两点坐标代入解析式得
,解得,∴y=﹣(x-1)2+,∴水流最高处距
出水口的竖直距离是-10=(m).
14.①②④ 解析:∵点A,B都在y2=的图象上,且AC⊥x轴,BD⊥y轴,∴S△ODB=S△OCA==,∴①对;∵点P在y1=的图象上,且PC⊥x轴,PD⊥y轴,∴S矩形ODPC==k(k>0),∴S四边形PAOB=S矩形ODPC―S△ODB―S△OCA=k――=k―1(常量),∴②对;(用特殊值法)设A(3,),B(,2),则P(3,2),D(0,2),C(3,0),∴PA=PC-AC=2-=,PB=PD-BD=3-=,∵≠,∴③错;∵点A是CP的中点,∴设P(m,n),则A(m,),∵S△ODB=S△OCA,∴×OC×AC=×OD×BD,∵OC=PD=m,AC=PC=OD,∴PD=BD,∴点B是PD的中点,∴④对.
15.解:如图,由题意知重叠部分为等腰直角三角形DAP,∵AE=3t,∴AD=DE-AE=30-3t,∴PD=DA=30-3t,∴y=×PD×AD=(30-3t)2=t2-90t+450,∵0≤AE≤30,∴0≤30-3t≤30,解得0≤t≤15,∴重叠部分的面积y(cm2)与时间t(s)之间的函数关系式为y=t2-90t+450,自变量t的取值范围是0≤t≤15.
17. 解:(1)∵抛物线y=a(x-3)2-6经过点(5,﹣2),∴把点(5,﹣2)代入解析式得a
×(5-3)2-6=﹣2,解得a=1,∴抛物线的解析式为y=(x-3)2-6=x2﹣6x
+3;
(2)∵抛物线y=(x-3)2-6的对称轴为直线x=3,∴点M(m,y1)和点N(n, y2)
(m<n<3)都在对称轴的左侧,又∵a=1,∴该抛物线开口向上,∴在对称轴
左侧(x<3),y随x的增大而减小,∵m<n<3,∴y1>y2.
18.解:(1)∵矩形面积S=xy(S≠0),∴y=,把S=1.2代入得y=,y是x
的反比例函数;
(2)∵长比宽多2.6m,∴y=x+2.6,代入解析式得x+2.6=,整理得x2+2.6x-1.2=0,解得x1=0.4,x2=﹣3(不合题意,舍去),∴矩形模具的宽为0.4m,长为0.4+2.6=3(m),∴矩形模具的周长为(0.4+3)×2=6.8(m),6.8×6.5=44.2(元),答:加工这个模具共需44.2元钱.
(2)证明:由题意得,消去y得x2-3x+3=0,∵△=b2-4ac=(﹣3)2-4×1×3=﹣3<0,∴此方程没有实数根,∴抛物线与直线l1没有公共点;
(3)由题意得,消去y得x2-3x-2+m2=0,∵直线l2:y=2x-m2与抛物线只有一个公共点,∴△=b2-4ac=(﹣3)2-4×1×(-2+m2)=0,解得m=±1,把代入方程x2-3x-2+m2=0解得x=,把x=代入y=x2-x-2得y=﹣,∴这个公共点的坐标为(,﹣).
20.解:(1)由题意得出口宽(50-2x)m,∴绿化区矩形较短边长为×[40-(50-2x)]=(x-5)m,∴y与x的函数关系式为y=25×4x(x-5)+30×[50×40-4x(x-5)]=﹣20x2+100x+60000=﹣20(x﹣2.5)2+60125,由题意得25≤50-2x≤30,解得10≤x≤12.5,∴y与x的函数关系式为y=﹣20x2+100x+60000,自变量x的取值范围是10≤x≤12.5;21教育网
(2)∵y=﹣20x2+100x+60000=﹣20(x﹣2.5)2+60125,﹣20<0,∴当x≥2.5时,y随x的增大而减小,又10≤x≤12.5,∴当x=12.5时,y最小=﹣20(12.5﹣2.5)2+60125=58125,此时x-5=12.5-5=7.5(m).答:当绿化区矩形长为12.5m,宽为7.5m时,投资最小,最小投资为58125元.
21.解:(1)在一次函数y=﹣x+2中,当x=0时,y=2,当y=0时,x=4,∴A(4,0),B(0,2),把A,B两点坐标代入y=﹣x2+bx+c得,解得,∴这个抛物线的解析式为y=﹣x2+x+2;
(2)∵直线x=n垂直于x轴,与y=﹣x+2交于点C,与抛物线y=﹣x2+x+2交于点D,∴C(n,﹣n+2),D(n,﹣n2+n+2),∵点C,D在第一象限,∴﹣n+2>0,﹣n2+n+2>0,∴CD=-=(﹣n2+n+2)-(﹣n+2)=﹣n2+4n=﹣(n﹣2)2+4,当n=2时,CD最大=4,∴当n=2时,CD有最大值,最大值为4;
(3)由题意可知E点可能在y轴上,也可能不在y轴上,如下图,当E点在y轴上时,设E(0,m),∵CD=BE=4,B(0,2),∴=4,∴m=﹣2或6,∴E(0,﹣2)或E(0,6),当E点不在y轴上时,将直线AB向上平移4个单位得直线E2E3,∴直线E2E3的解析式为y=﹣x+6①,设直线E1E3的解析式为y=kx+b,把点E1(0,﹣2),C(2,1),坐标代入得,解得,∴直线E1E3的解析式为y=x-2②,联立①②解得,∴E3(4,4),∴第四个顶点E的坐标为(0,﹣2)或(0,6)或(4,4).
22.解:(1)设y=kx+b,其图象经过点(60,5),(80,4),代入得,解得,∴y与x的函数关系式为y=﹣x+8;
(2)由题意得z=xy-40y-120=y(x-40)-120=(﹣x+8)(x-40)-120=﹣x2+10x-440=﹣(x-100)2+60,∵﹣<0,∴当x=100时,y最大=60,∴当销售单价定为100元时,年获利最大,最大值为60万元;
(3)由z=40得﹣(x-100)2+60=40,解得x1=80,x2=120,画出函数图象如下图,由图象可知要使年获利不低于40万元,销售单价应在80元到120元之间.又∵销售单价越低,销售量越大,∴销售单价应定为80元.
23.解:(1)设B点坐标为(a,b),∵B点在第一象限,∴S正方形OABC=ab=9,∵a=b,∴a=b=3,∴B点坐标为(3,3),又B点在y=的图象上,∴ab=9=k,∴反比例函数的解析式为y=;
(2)当点P在B点下方时,如图1,∵P(m,n)在y=上,∴mn=9,∴S矩形OEPF=mn=9,S矩形OADF=3n,∵S=S矩形OEPF-S矩形OADF,S=,∴9-3n=,∴n=,∴m=6,∴P点坐标为(6,);当点P在B点上方时,如图2,同理可得P点坐标为(,6).∴综上,P点坐标为(6,)或(,6);
(3)如图1,当m≥3时,∵P(m,n),∴S矩形OADF=3n,∵mn=9,∴n=, ∴S=9-3n=9-3×=9-;如图2,当0<m<3时,∵P(m,n),∴S=S矩形OEPF-S矩形OEDC=9-OC×OE=9-3m,∴S与m的函数关系式为S=.
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.已知函数y=(m2-2m)是关于x的二次函数,m为常数,则一次函数y=mx+m的图象一定不经过点……………………………………………………………【 】
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.关于x的二次函数y=x2在﹣1≤x≤3时的最值情况,以下说法正确的是…………【 】
A.最小值为1,最大值为9 B. 最小值为0,最大值为9
C. 最小值为1,没有最大值 D. 最小值为0,没有最大值
3.已知二次函数y=2(x-1)2+k的图象经过点A(,y1),B(2,y2),C(1-,y3)三点,则y1,y2,y3的大小关系是……………………………………………【 】
A. y1>y2>y3 B. y1>y3>y2 C. y3>y1>y2 D. y3>y2>y1
4.如图,二次函数y=ax2-4x+c的图象与y轴交于点A,且经过点B,点M,N也在此函数图象上,且点M,N关于此抛物线的对称轴对称,点M的坐标为(m, ﹣2m)(m<0),则点N到x轴的距离为…………………………………………………………【 】
A.2 B.4 C.6 D.8
5.如图,在□ABCD中,AB=2,D点坐标为(0,4),以点C为顶点的抛物线y=ax2+bx+c经过x轴上的点A,B,若将抛物线向上平移后恰好经过点D,则平移后的抛物线解析式为…………………………………………………………………………【 】
A. y=﹣4x2+16x-4 B. y=﹣4x2+16x+4
C. y=﹣4x2-16x+4 D. y=﹣4x2-16x-4
6.函数y=x2-x+m的图象如图所示,当x=a时,y<0,求当x=a-1时,y的值.我班五位同学在探究此题时各得到一条相关信息,甲:当x=0时,y=m>0;乙:抛物线的对称轴为直线x=;丙:x1<a<x2;丁:关键要判断a-1的符号;戊:m可以取一个特殊值.请参考这五位同学获得的信息,你的答案是………………………【 】
A. y<0 B.0<y<m C.y>m D.y=m
7.已知抛物线y=ax2+bx+c经过A(0,1)和B(2,﹣3)两点,且开口方向向下,若抛物线的对称轴在y轴右侧,则a的取值范围是…………………………………【 】
A. a<0 B. a<﹣1 C. ﹣1<a<0 D. a<﹣2
8.如图,有一座抛物线形拱桥,桥下正常水位为AB时,水面宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m,若洪水到来时,水位以0.4m/h的速度上升,则洪水从警戒线开始上升到达拱桥顶端所需的时间为………………………………【 】
A.1h B.1.5h C. 2h D. 2.5h
9.如图,是我校教室墙壁上的窗户示意图,它的上半部分是半圆,下半部分是矩形,制造这种窗框的材料总长(图中所有黑线的长度和)为15m,当窗户通过的光线最多时,半圆的半径(精确到0.1)应为………………………………………………………【 】
A.0.8m B.0.9m C. 1.0m D. 1.1m
10.如图,点A在反比例函数的图象上,过点A作AB⊥y轴于点B,点C在x轴上,△ABC的面积为3,则这个反比例函数的解析式为…………………………………【 】
A. y= B. y= C. y= D. y=
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知m,n,k均为非负实数,且m-k+1=2k+n=1,则代数式2k2-8k+6的最小值为_____________.21·cn·jy·com
12.如图,抛物线y=﹣x2+2(m+1)x+m+3与x轴交于A,B两点,且OA︰OB=3︰1,则m的值为___________.www.21-cn-jy.com
13.如图,是消防水枪喷水的示意图,出水口A点离地面10米,水流最高处距出水口的水平距离为1米,水流落地点B距出水口的水平距离为3米,则水流最高处距出水口的竖直距离是_______________米.
14.如图,反比例函数y1=和y2=的图象都在第一象限,点P在y1=的图象上,PC⊥x轴于点C,交y2=的图象于点A,PD⊥y轴于点D,交y2=的图象于点B,当点P在y1=的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是_________________(把你认为正确的结论的序号填在横线上).
三、(本大题共两小题,每小题8分,满分16分)
15.如图,已知等腰直角三角形ABC的直角边长与正方形DEFG的边长均为30cm,AC与DE在同一条直线上,开始时点A与点E重合,让△ABC以3cm/s的速度向左运动,最终点A与点D重合,求重叠部分的面积y(cm2)与时间t(s)之间的函数关系式并写出自变量t的取值范围.
16.已知二次函数的图象经过点A(﹣1,0)和点B(2,﹣1),其对称轴是直线x=1,求这个二次函数的解析式. 21*cnjy*com
四、(本大题共两小题,每小题8分,满分16分)
17.已知抛物线y=a(x-3)2-6经过点(5,﹣2).
(1)求抛物线的解析式;
(2)若点M(m,y1)和点N(n, y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
18.解师傅想利用一种不锈钢条为边加工一个面积为1.2m2的矩形模具,设模具的长为ym,宽为xm.
(1)请写出y与x的函数关系式,y与x是什么函数关系?
(2)要使模具的长比宽多2.6m,已知这种不锈钢条每米6.5元,试求加工这个模具共需多少钱?
五、(本大题共两小题,每小题10分,满分20分)
19.已知抛物线y=ax2+bx-2经过A(﹣1,0)、B(1,﹣2)两点,直线l1:y=2x-5.21世纪教育网版权所有
(1)求抛物线的解析式;
(2)求证:抛物线与直线l1没有公共点;
(3)若与直线l1平行的直线l2:y=2x-m2与抛物线只有一个公共点,求这个公共点的坐标.
20.某小内有一块长50m、宽40m的空地,现要将其建成广场,设计图案如图,阴影区域为绿化区(四块绿化区是全等矩形),空白区域是活动区,且四周出口一样宽,宽度不小于25m,不大于30m,预计活动区造价30元/平方米,绿化区造价25元/平方米.2·1·c·n·j·y
(1)设绿化区矩形较长的边长为xm,试写出工程总造价y(元)与x的函数关系式,并写出自变量的取值范围;www-2-1-cnjy-com
(2)请你设计一种投资最小的方案,并求出最小投资.
六、(本题满分12分)
21.如图,一次函数y=﹣x+2分别交x轴、y轴于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点.21·世纪*教育网
(1)求这个抛物线的解析式;
(2)作垂直于x轴的直线x=n,在第一象限交直线AB于点C,交这个抛物线于点D,求当n取何值时,CD有最大值?最大值是多少? 【来源:21·世纪·教育·网】
(3)在(2)的条件下,以B,C,D,E为顶点作平行四边形,试求第四个顶点E的坐标.
七、(本题满分12分)
22.当前,广场舞风靡全球,某服装超市从中发现商机,决定销售一款超短裙.已知每件超短裙的进价为40元,每年销售该款超短裙的总开支(不含进价)共计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在如图所示的一次函数关系. 21*cnjy*com
(1)求y与x的函数关系式;
(2)试写出该超市销售该款超短裙的年获利z(万元)与销售单价x(元)的函数关系式(年获利=年销售额-年总进价-年总开支).当超市希望该款超短裙年获利不低于40万元,试画出函数图象,并帮该超市确定销售单价的范围.在此情况下,要使该款超短裙销量最大,你认为销售单价应定为多少元?
八、(本题满分14分)
23.如图,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在反比例函数y=(k>0,x>0)的图象上,点P(m,n)是反比例函数y=(k>0,x>0)的图象上任意一点,过点P分别作PE⊥x轴于点E,PF⊥y轴于点F,设矩形OEPF与正方形OABC不重合部分的面积为S.
(1)求B点坐标和反比例函数的解析式;
(2)当S=时,求点P的坐标;
(3)写出S关于m的函数关系式.
参考答案
1.A 解析:由题意得,解得m=﹣1,∴一次函数解析式为y=﹣x-1,它的图象经过第二、三、四象限,∴选A. 2-1-c-n-j-y
2. B 解析:当﹣1≤x<0时,0<y≤1;当x=0时,y=0,;当0<x≤3时,0<y≤9.∴综
上,当﹣1≤x≤3时,y最小=0,y最大=9,∴选B.
3.C解析:画出函数的大致图象,如下图,∵2>0,∴图象上距离对称轴越近的点,其纵坐标越小,∵-1<1.3,2-1=1,+1=>1.7,∴>-1>1,∴B点距离对称轴最近,C点距离对称轴最远,∴y3>y1>y2,∴选C.(本题也可用代入法:把A,B,C三点的横坐标代入,计算后再比较大小)
4.A 解析:把点A(0,﹣3),B(3,﹣7)代入y=ax2-4x+c得,解得a=1,c=﹣3,∴y=x2-4x-3,其对称轴为直线x=﹣=1,把点M(m, ﹣2m)代入得m2-4m-3=﹣2m,解得m1=﹣1,m2=3,∵m<0,∴m=﹣1,∴M(﹣1, 2),∵点M,N关于此抛物线的对称轴对称,∴N(3,2),∴点N到x轴的距离为2,∴选A. 【来源:21cnj*y.co*m】
5.B 解析:∵AB=CD=2,AB∥CD,D(0,4),∴C(2,4),
如下图,设抛物线对称轴与x轴交于点H,
由抛物线的对称轴可得H为AB的中点,
∴AH=1,又DC=OH=2,∴OA=1,∴A(1,0),
设抛物线解析式为y=a(x-2)2+4,把A(1,0)代入得a=﹣4,
∴y=﹣4 (x-2)2+4,
设向上平移后的抛物线解析式为y=﹣4 (x-2)2+4+k,把D(0,4)代入解得k=16,
∴向上平移后的抛物线解析式为y=﹣4 (x-2)2+4+16=﹣4x2+16x+4.
6.C 解析:∵抛物线的对称轴为x=,∴<x2<1,又x1<a<x2,∴a<1,∴a-1<0,∵x=0时,y=m,∴观察图象可得当x=a-1时,y>m,∴选C.
7.B 解析:∵抛物线开口向下,∴a<0,又∵抛物线对称轴在y轴右侧,∴﹣>0,∴b>0,把点(0,1)和(2,﹣3)代入y=ax2+bx+c得,∴2a+b=﹣2,∴b=﹣2-2a,∴﹣2-2a>0,解得a<﹣1,解不等式得a<﹣1,∴选B 21cnjy.com
8.D 解析:设拱桥所在抛物线的解析式为y=ax2,由题意设D点坐标为(5,n),则B点坐标为(10,n-3),将B,D两点坐标代入解析式得,解得,∴洪水从警戒线开始上升到达拱桥顶端所需的时间为==2.5(h),∴选D. 【出处:21教育名师】
9.D 解析:设半圆的半径为xm,小矩形的竖直边长为ym,由题意得y=,设窗户的面积为S,则S=x2+2xy=x2+2x×=﹣3.5 x2+7.5x ,∵﹣3.5<0,∴当x=﹣≈1.1时,S最大=≈4.0,∴选D. 【版权所有:21教育】
10.C 解析:如下图,连接OA,∵AB∥x轴,∴S△OAB=S△ABC=3,设反比例函数解析式为y=,由反比例函数的性质可得S△OAB=,∴=6,∵函数图象在第三象限,∴k>0,∴k=6,∴y=,∴选C .21教育名师原创作品
11.2.5 解析:∵m,n,k均为非负实数,∴m,n,k的最小值均为0,又∵2k+n=1,∴当n最小为0时,k最大为,∴0≤k≤,∵2k2-8k+6=2(k-2)2-2,∴当k≤2时,代数式2k2-8k+6的值随k的增大而减小,∴当k=时,代数式2k2-8k+6取得最小值,为2×()2-8×+6=2.5.
12.0 解析:设A(x1,0),B(x2,0),∵OA︰OB=3︰1,∴x2=﹣3x1,观察图象得抛物线
与x轴有两个交点,∴方程﹣x2+2(m+1)x+m+3=0有两个不相等的实数根,
由韦达定理得x1+x2=2(m+1),x1x2=﹣(m+3),把x2=﹣3x1分别代入得
,消去x1得3(m+1)2=m+3,解得m1=0,m2=﹣,观察
图象得x1<0,x2>0,<,∴x1+x2>0,当m=﹣时,x1+x2=﹣<
0,∴m=﹣不合题意,舍去,∴m=0.
13. 解析:由题意知抛物线顶点横坐标为1,∴可设抛物线解析式为y=a(x-1)2+k,
由题意知抛物线经过点A(0,10)、B(3,0),把这两点坐标代入解析式得
,解得,∴y=﹣(x-1)2+,∴水流最高处距
出水口的竖直距离是-10=(m).
14.①②④ 解析:∵点A,B都在y2=的图象上,且AC⊥x轴,BD⊥y轴,∴S△ODB=S△OCA==,∴①对;∵点P在y1=的图象上,且PC⊥x轴,PD⊥y轴,∴S矩形ODPC==k(k>0),∴S四边形PAOB=S矩形ODPC―S△ODB―S△OCA=k――=k―1(常量),∴②对;(用特殊值法)设A(3,),B(,2),则P(3,2),D(0,2),C(3,0),∴PA=PC-AC=2-=,PB=PD-BD=3-=,∵≠,∴③错;∵点A是CP的中点,∴设P(m,n),则A(m,),∵S△ODB=S△OCA,∴×OC×AC=×OD×BD,∵OC=PD=m,AC=PC=OD,∴PD=BD,∴点B是PD的中点,∴④对.
15.解:如图,由题意知重叠部分为等腰直角三角形DAP,∵AE=3t,∴AD=DE-AE=30-3t,∴PD=DA=30-3t,∴y=×PD×AD=(30-3t)2=t2-90t+450,∵0≤AE≤30,∴0≤30-3t≤30,解得0≤t≤15,∴重叠部分的面积y(cm2)与时间t(s)之间的函数关系式为y=t2-90t+450,自变量t的取值范围是0≤t≤15.
17. 解:(1)∵抛物线y=a(x-3)2-6经过点(5,﹣2),∴把点(5,﹣2)代入解析式得a
×(5-3)2-6=﹣2,解得a=1,∴抛物线的解析式为y=(x-3)2-6=x2﹣6x
+3;
(2)∵抛物线y=(x-3)2-6的对称轴为直线x=3,∴点M(m,y1)和点N(n, y2)
(m<n<3)都在对称轴的左侧,又∵a=1,∴该抛物线开口向上,∴在对称轴
左侧(x<3),y随x的增大而减小,∵m<n<3,∴y1>y2.
18.解:(1)∵矩形面积S=xy(S≠0),∴y=,把S=1.2代入得y=,y是x
的反比例函数;
(2)∵长比宽多2.6m,∴y=x+2.6,代入解析式得x+2.6=,整理得x2+2.6x-1.2=0,解得x1=0.4,x2=﹣3(不合题意,舍去),∴矩形模具的宽为0.4m,长为0.4+2.6=3(m),∴矩形模具的周长为(0.4+3)×2=6.8(m),6.8×6.5=44.2(元),答:加工这个模具共需44.2元钱.
(2)证明:由题意得,消去y得x2-3x+3=0,∵△=b2-4ac=(﹣3)2-4×1×3=﹣3<0,∴此方程没有实数根,∴抛物线与直线l1没有公共点;
(3)由题意得,消去y得x2-3x-2+m2=0,∵直线l2:y=2x-m2与抛物线只有一个公共点,∴△=b2-4ac=(﹣3)2-4×1×(-2+m2)=0,解得m=±1,把代入方程x2-3x-2+m2=0解得x=,把x=代入y=x2-x-2得y=﹣,∴这个公共点的坐标为(,﹣).
20.解:(1)由题意得出口宽(50-2x)m,∴绿化区矩形较短边长为×[40-(50-2x)]=(x-5)m,∴y与x的函数关系式为y=25×4x(x-5)+30×[50×40-4x(x-5)]=﹣20x2+100x+60000=﹣20(x﹣2.5)2+60125,由题意得25≤50-2x≤30,解得10≤x≤12.5,∴y与x的函数关系式为y=﹣20x2+100x+60000,自变量x的取值范围是10≤x≤12.5;21教育网
(2)∵y=﹣20x2+100x+60000=﹣20(x﹣2.5)2+60125,﹣20<0,∴当x≥2.5时,y随x的增大而减小,又10≤x≤12.5,∴当x=12.5时,y最小=﹣20(12.5﹣2.5)2+60125=58125,此时x-5=12.5-5=7.5(m).答:当绿化区矩形长为12.5m,宽为7.5m时,投资最小,最小投资为58125元.
21.解:(1)在一次函数y=﹣x+2中,当x=0时,y=2,当y=0时,x=4,∴A(4,0),B(0,2),把A,B两点坐标代入y=﹣x2+bx+c得,解得,∴这个抛物线的解析式为y=﹣x2+x+2;
(2)∵直线x=n垂直于x轴,与y=﹣x+2交于点C,与抛物线y=﹣x2+x+2交于点D,∴C(n,﹣n+2),D(n,﹣n2+n+2),∵点C,D在第一象限,∴﹣n+2>0,﹣n2+n+2>0,∴CD=-=(﹣n2+n+2)-(﹣n+2)=﹣n2+4n=﹣(n﹣2)2+4,当n=2时,CD最大=4,∴当n=2时,CD有最大值,最大值为4;
(3)由题意可知E点可能在y轴上,也可能不在y轴上,如下图,当E点在y轴上时,设E(0,m),∵CD=BE=4,B(0,2),∴=4,∴m=﹣2或6,∴E(0,﹣2)或E(0,6),当E点不在y轴上时,将直线AB向上平移4个单位得直线E2E3,∴直线E2E3的解析式为y=﹣x+6①,设直线E1E3的解析式为y=kx+b,把点E1(0,﹣2),C(2,1),坐标代入得,解得,∴直线E1E3的解析式为y=x-2②,联立①②解得,∴E3(4,4),∴第四个顶点E的坐标为(0,﹣2)或(0,6)或(4,4).
22.解:(1)设y=kx+b,其图象经过点(60,5),(80,4),代入得,解得,∴y与x的函数关系式为y=﹣x+8;
(2)由题意得z=xy-40y-120=y(x-40)-120=(﹣x+8)(x-40)-120=﹣x2+10x-440=﹣(x-100)2+60,∵﹣<0,∴当x=100时,y最大=60,∴当销售单价定为100元时,年获利最大,最大值为60万元;
(3)由z=40得﹣(x-100)2+60=40,解得x1=80,x2=120,画出函数图象如下图,由图象可知要使年获利不低于40万元,销售单价应在80元到120元之间.又∵销售单价越低,销售量越大,∴销售单价应定为80元.
23.解:(1)设B点坐标为(a,b),∵B点在第一象限,∴S正方形OABC=ab=9,∵a=b,∴a=b=3,∴B点坐标为(3,3),又B点在y=的图象上,∴ab=9=k,∴反比例函数的解析式为y=;
(2)当点P在B点下方时,如图1,∵P(m,n)在y=上,∴mn=9,∴S矩形OEPF=mn=9,S矩形OADF=3n,∵S=S矩形OEPF-S矩形OADF,S=,∴9-3n=,∴n=,∴m=6,∴P点坐标为(6,);当点P在B点上方时,如图2,同理可得P点坐标为(,6).∴综上,P点坐标为(6,)或(,6);
(3)如图1,当m≥3时,∵P(m,n),∴S矩形OADF=3n,∵mn=9,∴n=, ∴S=9-3n=9-3×=9-;如图2,当0<m<3时,∵P(m,n),∴S=S矩形OEPF-S矩形OEDC=9-OC×OE=9-3m,∴S与m的函数关系式为S=.
