湖北省武汉市2023—2024学年下学期开学考九年级数学试题(pdf版无答案)
文档属性
| 名称 | 湖北省武汉市2023—2024学年下学期开学考九年级数学试题(pdf版无答案) |  | |
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 18:29:01 | ||
图片预览

文档简介
九年级阶段性检测数学试卷
一、选择题(共 10 小题,每小题 3 分,共 30 分)
1.下列各组图形一定相似的是( )
A.任意两个平行四边形 B.任意两个矩形 C.任意两个菱形 D.任意两个正方形
2.已知反比例函数 = 图像经过点 2,3 ,下列说法中不正确的是( )
A.该函数图象在第二、四象限 B.点 1, 6 在该函数图象上
C. 随 的增大而增大 D.当 > 1 时, 6 y 0
3.如图,一个梯子靠在垂直水平地面的墙上,梯子 AB 的长是 2米.若梯子与地面的夹角为
,则梯子顶端到地面的距离(BC 的长)为( )
2sin 2cos 2 2A. 米 B. 米 C. 米 D. 米
sin cos
1
4.若点 2, 1 , 1, 2 , 1, 3 都在反比例 = 函数的图象上,则( )
A. 1 > 2 > 3 B. 3 > 1 > 2
C. 2 > 1 > 3 D. 1 > 3 > 2
1
5.如图,在△ABC 中,sinB= , tanC=2,AB=3,则 AC 的长为( )
3
A. 2 B. 5 C. 5 D.2
2
6.如图,△ABC的顶点都是正方形网格中的格点,则 sin∠CAB等于( )
A. B. C. D.2
2+1
7. 已知点 1, 1 , 2, 2 在反比例函数 = ( 为常数)的图象上,且 1 < 0 < 2,
则下列结论一定正确的是( )
A. 1 + 2 < 0 B. 1 + 2 > 0 C. 1 < 2 D. 1 > 2
8.如图,在△ABC 中,DE∥FG∥BC,且 AD:AF:AB=1:2:4,则 S△ADE:S 四边形 DFGE:S 四边形 FBCG
等于( )
A.1:2:4 B.1:4:16 C.1:3:12 D.1:3:7
第 8 题 第 9 题 第 10 题
第 1页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
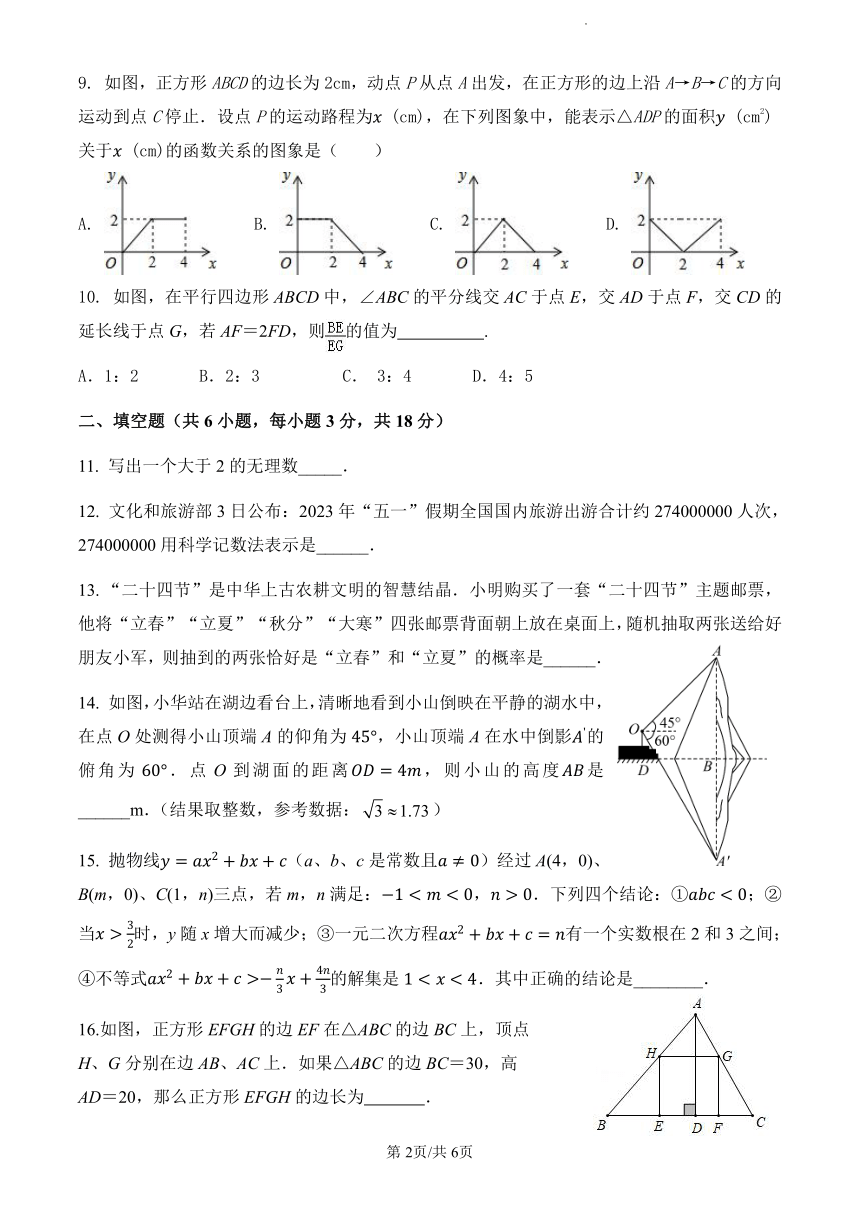
9. 如图,正方形 ABCD 的边长为 2cm,动点 P从点 A出发,在正方形的边上沿 A→B→C的方向
运动到点 C停止.设点 P的运动路程为 (cm),在下列图象中,能表示△ADP 的面积 (cm2)
关于 (cm)的函数关系的图象是( )
A. B. C. D.
10. 如图,在平行四边形 ABCD中,∠ABC的平分线交 AC于点 E,交 AD于点 F,交 CD的
延长线于点 G,若 AF=2FD,则 的值为 .
A.1:2 B.2:3 C. 3:4 D.4:5
二、填空题(共 6 小题,每小题 3 分,共 18 分)
11. 写出一个大于 2的无理数_____.
12. 文化和旅游部 3日公布:2023年“五一”假期全国国内旅游出游合计约 274000000人次,
274000000用科学记数法表示是______.
13.“二十四节”是中华上古农耕文明的智慧结晶.小明购买了一套“二十四节”主题邮票,
他将“立春”“立夏”“秋分”“大寒”四张邮票背面朝上放在桌面上,随机抽取两张送给好
朋友小军,则抽到的两张恰好是“立春”和“立夏”的概率是______.
14. 如图,小华站在湖边看台上,清晰地看到小山倒映在平静的湖水中,
在点 O处测得小山顶端 A的仰角为 45°,小山顶端 A在水中倒影 '的
俯角为 60°.点 O 到湖面的距离 = 4 ,则小山的高度 是
______m.(结果取整数,参考数据: 3 1.73)
15. 抛物线 = 2 + + (a、b、c是常数且 ≠ 0)经过 A(4,0)、
B(m,0)、C(1,n)三点,若 m,n满足: 1 < < 0, > 0.下列四个结论:① < 0;②
当 > 3时,y随 x增大而减少;③一元二次方程 2 + + = 有一个实数根在 2和 3之间;2
④不等式 2 + + > + 4 的解集是 1 < < 4.其中正确的结论是________.
3 3
16.如图,正方形 EFGH的边 EF在△ABC的边 BC上,顶点
H、G分别在边 AB、AC上.如果△ABC的边 BC=30,高
AD=20,那么正方形 EFGH的边长为 .
第 2页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
三、解答题(共 8 小题,共 72 分)
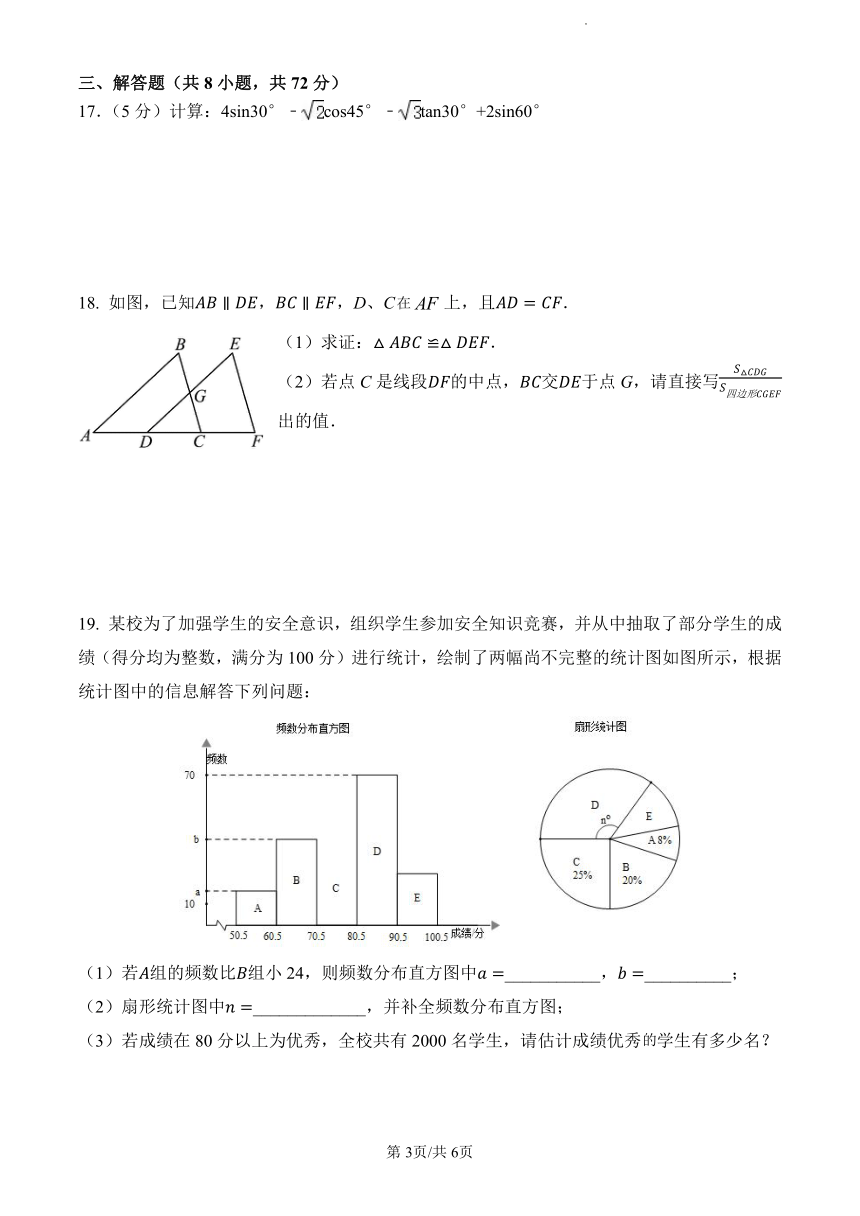
17.(5分)计算:4sin30°﹣ cos45°﹣ tan30°+2sin60°
18. 如图,已知 ∥ , ∥ ,D、C在 AF 上,且 = .
(1)求证:△ ≌△ .
△
(2)若点 C是线段 的中点, 交 于点 G,请直接写
四边形
出的值.
19. 某校为了加强学生的安全意识,组织学生参加安全知识竞赛,并从中抽取了部分学生的成
绩(得分均为整数,满分为 100分)进行统计,绘制了两幅尚不完整的统计图如图所示,根据
统计图中的信息解答下列问题:
(1)若 组的频数比 组小 24,则频数分布直方图中 =___________, =__________;
(2)扇形统计图中 =_____________,并补全频数分布直方图;
(3)若成绩在 80分以上为优秀,全校共有 2000名学生,请估计成绩优秀的学生有多少名?
第 3页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
20. 如图,⊙O是△ABC的外接圆,AB=AC,BO的延长线交 AC于点 D.
(1)求证:∠BAC=2∠ABD;
(2 )若 = 2,求 tan∠ABD.
3
k
21. 如图,一次函数 y x 4的图象与反比例函数 y ( k为常数且 k 0)的图象交于 A(1,a),
x
B两点,与 y轴交于点C.
(1)求反比例函数的表达式与 B点坐标;
(2) k请直接写出不等式 x 4 x的解集;
(3)若点 P是线段BC上的一个动点,作 PQ∥ y轴交反比例函数 y
k
x
的图象于点Q,则△PCQ的面积的最大值为______.
第 4页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
22.(8分)如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对
岸一幢建筑物 BC的高度,他们先在斜坡上的 D处,测得建筑物顶端 B的仰角为 30°.且 D
离地面的高度 DE=5m.坡底 EA=30m,然后在 A处测得建筑物顶端 B的仰角是 60°,点 E,
A,C在同一水平线上,求建筑物 BC的高.(结果用含有根号的式子表示)
23.(10分)如图,在矩形 ABCD中,AB=20,点 E是 BC边上的一点,将△ABE沿着 AE折
叠,点 B刚好落在 CD边上点 G处;点 F在 DG上,将△ADF沿着 AF折叠,点 D刚好落在
AG上点 H处,此时 S△GFH:S△AFH=2:3,
(1)求证:△EGC∽△GFH;
(2)求 AD的长;
(3)求 tan∠GFH的值.
第 5页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
24. 如图,抛物线 = 2 4 + 3 交 轴于 , 两点(点 在点 的左侧),交 轴正半轴于
点 , = ,点 在抛物线上.
(1)求抛物线的解析式;
(2)若 ∠ = 2,求点 的横坐标.
(3)平面上有两点 , 3 , + 2, 5 ,求△ 的面积的最小值;
第 6页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
一、选择题(共 10 小题,每小题 3 分,共 30 分)
1.下列各组图形一定相似的是( )
A.任意两个平行四边形 B.任意两个矩形 C.任意两个菱形 D.任意两个正方形
2.已知反比例函数 = 图像经过点 2,3 ,下列说法中不正确的是( )
A.该函数图象在第二、四象限 B.点 1, 6 在该函数图象上
C. 随 的增大而增大 D.当 > 1 时, 6 y 0
3.如图,一个梯子靠在垂直水平地面的墙上,梯子 AB 的长是 2米.若梯子与地面的夹角为
,则梯子顶端到地面的距离(BC 的长)为( )
2sin 2cos 2 2A. 米 B. 米 C. 米 D. 米
sin cos
1
4.若点 2, 1 , 1, 2 , 1, 3 都在反比例 = 函数的图象上,则( )
A. 1 > 2 > 3 B. 3 > 1 > 2
C. 2 > 1 > 3 D. 1 > 3 > 2
1
5.如图,在△ABC 中,sinB= , tanC=2,AB=3,则 AC 的长为( )
3
A. 2 B. 5 C. 5 D.2
2
6.如图,△ABC的顶点都是正方形网格中的格点,则 sin∠CAB等于( )
A. B. C. D.2
2+1
7. 已知点 1, 1 , 2, 2 在反比例函数 = ( 为常数)的图象上,且 1 < 0 < 2,
则下列结论一定正确的是( )
A. 1 + 2 < 0 B. 1 + 2 > 0 C. 1 < 2 D. 1 > 2
8.如图,在△ABC 中,DE∥FG∥BC,且 AD:AF:AB=1:2:4,则 S△ADE:S 四边形 DFGE:S 四边形 FBCG
等于( )
A.1:2:4 B.1:4:16 C.1:3:12 D.1:3:7
第 8 题 第 9 题 第 10 题
第 1页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
9. 如图,正方形 ABCD 的边长为 2cm,动点 P从点 A出发,在正方形的边上沿 A→B→C的方向
运动到点 C停止.设点 P的运动路程为 (cm),在下列图象中,能表示△ADP 的面积 (cm2)
关于 (cm)的函数关系的图象是( )
A. B. C. D.
10. 如图,在平行四边形 ABCD中,∠ABC的平分线交 AC于点 E,交 AD于点 F,交 CD的
延长线于点 G,若 AF=2FD,则 的值为 .
A.1:2 B.2:3 C. 3:4 D.4:5
二、填空题(共 6 小题,每小题 3 分,共 18 分)
11. 写出一个大于 2的无理数_____.
12. 文化和旅游部 3日公布:2023年“五一”假期全国国内旅游出游合计约 274000000人次,
274000000用科学记数法表示是______.
13.“二十四节”是中华上古农耕文明的智慧结晶.小明购买了一套“二十四节”主题邮票,
他将“立春”“立夏”“秋分”“大寒”四张邮票背面朝上放在桌面上,随机抽取两张送给好
朋友小军,则抽到的两张恰好是“立春”和“立夏”的概率是______.
14. 如图,小华站在湖边看台上,清晰地看到小山倒映在平静的湖水中,
在点 O处测得小山顶端 A的仰角为 45°,小山顶端 A在水中倒影 '的
俯角为 60°.点 O 到湖面的距离 = 4 ,则小山的高度 是
______m.(结果取整数,参考数据: 3 1.73)
15. 抛物线 = 2 + + (a、b、c是常数且 ≠ 0)经过 A(4,0)、
B(m,0)、C(1,n)三点,若 m,n满足: 1 < < 0, > 0.下列四个结论:① < 0;②
当 > 3时,y随 x增大而减少;③一元二次方程 2 + + = 有一个实数根在 2和 3之间;2
④不等式 2 + + > + 4 的解集是 1 < < 4.其中正确的结论是________.
3 3
16.如图,正方形 EFGH的边 EF在△ABC的边 BC上,顶点
H、G分别在边 AB、AC上.如果△ABC的边 BC=30,高
AD=20,那么正方形 EFGH的边长为 .
第 2页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
三、解答题(共 8 小题,共 72 分)
17.(5分)计算:4sin30°﹣ cos45°﹣ tan30°+2sin60°
18. 如图,已知 ∥ , ∥ ,D、C在 AF 上,且 = .
(1)求证:△ ≌△ .
△
(2)若点 C是线段 的中点, 交 于点 G,请直接写
四边形
出的值.
19. 某校为了加强学生的安全意识,组织学生参加安全知识竞赛,并从中抽取了部分学生的成
绩(得分均为整数,满分为 100分)进行统计,绘制了两幅尚不完整的统计图如图所示,根据
统计图中的信息解答下列问题:
(1)若 组的频数比 组小 24,则频数分布直方图中 =___________, =__________;
(2)扇形统计图中 =_____________,并补全频数分布直方图;
(3)若成绩在 80分以上为优秀,全校共有 2000名学生,请估计成绩优秀的学生有多少名?
第 3页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
20. 如图,⊙O是△ABC的外接圆,AB=AC,BO的延长线交 AC于点 D.
(1)求证:∠BAC=2∠ABD;
(2 )若 = 2,求 tan∠ABD.
3
k
21. 如图,一次函数 y x 4的图象与反比例函数 y ( k为常数且 k 0)的图象交于 A(1,a),
x
B两点,与 y轴交于点C.
(1)求反比例函数的表达式与 B点坐标;
(2) k请直接写出不等式 x 4 x的解集;
(3)若点 P是线段BC上的一个动点,作 PQ∥ y轴交反比例函数 y
k
x
的图象于点Q,则△PCQ的面积的最大值为______.
第 4页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
22.(8分)如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对
岸一幢建筑物 BC的高度,他们先在斜坡上的 D处,测得建筑物顶端 B的仰角为 30°.且 D
离地面的高度 DE=5m.坡底 EA=30m,然后在 A处测得建筑物顶端 B的仰角是 60°,点 E,
A,C在同一水平线上,求建筑物 BC的高.(结果用含有根号的式子表示)
23.(10分)如图,在矩形 ABCD中,AB=20,点 E是 BC边上的一点,将△ABE沿着 AE折
叠,点 B刚好落在 CD边上点 G处;点 F在 DG上,将△ADF沿着 AF折叠,点 D刚好落在
AG上点 H处,此时 S△GFH:S△AFH=2:3,
(1)求证:△EGC∽△GFH;
(2)求 AD的长;
(3)求 tan∠GFH的值.
第 5页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
24. 如图,抛物线 = 2 4 + 3 交 轴于 , 两点(点 在点 的左侧),交 轴正半轴于
点 , = ,点 在抛物线上.
(1)求抛物线的解析式;
(2)若 ∠ = 2,求点 的横坐标.
(3)平面上有两点 , 3 , + 2, 5 ,求△ 的面积的最小值;
第 6页/共 6页
{#{QQABBYSUggAIAAA网A(北京A)股份有Q限公司gCEwWYCgCQkBGAACoGAEAEsAAByQFABAA=}#}
同课章节目录
