北京市汇文教育集团垂杨柳学校2023—2024学年下学期九年级开学考数学试卷(PDF版、无答案)
文档属性
| 名称 | 北京市汇文教育集团垂杨柳学校2023—2024学年下学期九年级开学考数学试卷(PDF版、无答案) |

|
|
| 格式 | |||
| 文件大小 | 777.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 00:00:00 | ||
图片预览



文档简介
初三数学试卷
班级: 姓名: 成绩:
一、选择题(本题共 16 分,每题 2 分)第 1 - 8 题均有四个选项,符合题意的选项只有一个.
1. 抛物线 = ( + 2)2 1的对称轴是
A. = 1 B. = 1 C. = 2 D. = 2
2.下面的图形中,既是轴对称图形又是中心对称图形的是
A. B. C. D.
3.在下列事件中,随机事件是
A.投掷一枚质地均匀的骰子,向上一面的点数不超过 6
B.从装满红球的袋子中随机摸出一个球,是白球
C.通常情况下,自来水在 10℃结冰
D.投掷一枚质地均匀的骰子,向上一面的点数为 2
4. 如图,AB 是⊙O 的直径,C,D 是⊙O 上的两点.若∠CAB=65°,则∠ADC 的度数为
A.65° B.35°
C.32.5° D.25°
5.如果甲、乙、丙三位同学随机站成一排,那么甲站在中间的概率是
1 1 2 1
A. B. C. D.
2 6 3 3
6.平面直角坐标系 xOy 中,若点 ( 1, 2)和 ( 2, 4)在反比例函数 = ( > 0)图象上,则下列关系式
正确的是
A. 1 > 2 > 0 B. 2 > 1 > 0 C. 1 < 2 < 0 D. 2 < 1 < 0
7.某商店在节日期间开展优惠促销活动:购买原价超过 200 元的商品,超.过.200
元的部分可以享受打折优惠.若购买商品的实际付款金额 y(单位:元)与商
品原价 x(单位:元)的函数关系的图象如图所示,则超.过.200 元的部分可以
享受的优惠是( )
A.打八折 B.打七折 C.打六折 D.打五折
1
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
8.如图,正方形 ABCD 的边长是 4,E 是 AB 上一点,F 是 AD 延长线上的一
A D F
点,且 BE=DF,四边形 AEGF 是矩形,设 BE 的长为 x,AE 的长为 y,
矩形 AEGF 的面积为 S,则 y 与 x,S 与 x 满足的函数关系分别是 E
G
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系 B C
C.一次函数关系,反比例函数关系 D.反比例函数关系,一次函数关系
二、填空题(本题共 16 分,每题 2 分)
9.点 M(2,-4),N 关于原点对称,则点 N 的坐标是 .
10.已知⊙O 的半径为 6,若点 P 在⊙O 外,则 OP 6(填“>”“=”或“<”).
11. 如果一个圆锥的母线长为 4,底面半径为 1,那么这个圆锥的侧面积为 .
12.“圆”是中国文化的一个重要精神元素,在中式建筑
中有着广泛的应用,例如古典园林中的门洞,如图,
某地园林中的一个圆弧形门洞的高为 2.5m,地面入口
宽为 1m,则该门洞的半径为__________m.
13.为了解某小麦品种的发芽率,某农业合作小组在相同条件下对该小麦做发芽试验,试验数据如下
表:
种子个数 n 5 50 100 200 500 1 000 2 000 3 000
发芽种子个数 m 4 44 92 189 476 951 1 898 2 851
发芽种子频率 0.800 0.880 0.920 0.945 0.952 0.951 0.949 0.950
(1)估计该品种小麦在相同条件下发芽的概率为 (结果保留两位小数);
(2)若在相同条件下播种该品种小麦种子 10 000 个,则约有 个能发芽.
14.中国邮政集团公司曾发行《二十四节气》特殊版式小全张(图 1),其中的 24 枚邮票大小相同,
上面绘制了代表二十四节气风貌的图案,这 24 枚邮票组成了一个圆环,传达了四季周而复始、气
韵流动的理念和中国传统文化中圆满、圆融的概念.以“大雪”节气单枚邮票为例(图 2),该邮票
的“上圆弧”的长为 l,“直边长”为 d,“下圆弧”的长为 x,则 x= (用含 l,
d 的式子表示).
2
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
5
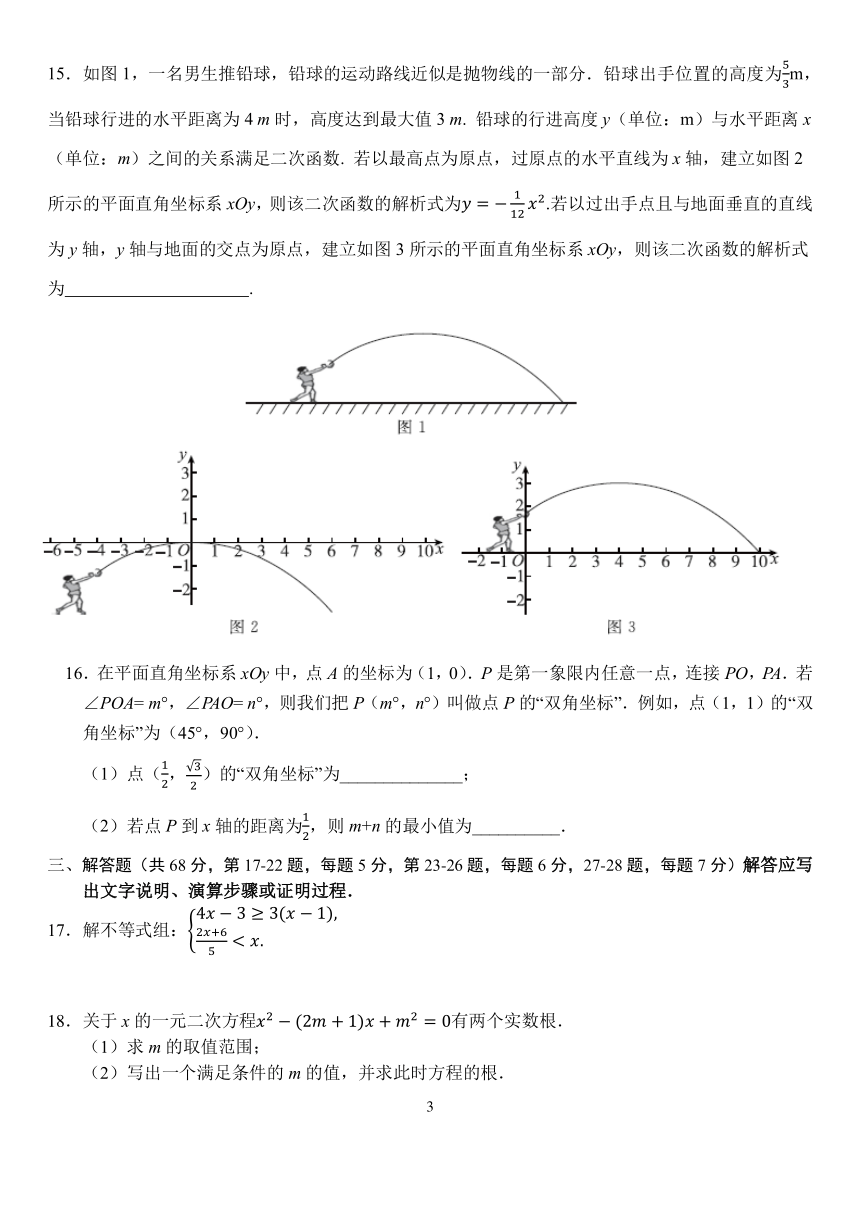
15.如图 1,一名男生推铅球,铅球的运动路线近似是抛物线的一部分.铅球出手位置的高度为 m,
3
当铅球行进的水平距离为 4 m 时,高度达到最大值 3 m. 铅球的行进高度 y(单位:m)与水平距离 x
(单位:m)之间的关系满足二次函数. 若以最高点为原点,过原点的水平直线为 x 轴,建立如图 2
1
所示的平面直角坐标系 xOy,则该二次函数的解析式为 = 2.若以过出手点且与地面垂直的直线
12
为 y 轴,y 轴与地面的交点为原点,建立如图 3 所示的平面直角坐标系 xOy,则该二次函数的解析式
为 .
16.在平面直角坐标系 xOy 中,点 A 的坐标为(1,0).P 是第一象限内任意一点,连接 PO,PA.若
∠POA= m°,∠PAO= n°,则我们把 P(m°,n°)叫做点 P 的“双角坐标”.例如,点(1,1)的“双
角坐标”为(45°,90°).
1 3
( √1)点( , )的“双角坐标”为______________;
2 2
1
(2)若点 P 到 x 轴的距离为 ,则 m+n 的最小值为__________.
2
三、解答题(共 68 分,第 17-22 题,每题 5 分,第 23-26 题,每题 6 分,27-28 题,每题 7 分)解答应写
出文字说明、演算步骤或证明过程.
4 3 ≥ 3( 1),
17.解不等式组:{2 +6
< .
5
18.关于 x 的一元二次方程 2 (2 + 1) + 2 = 0有两个实数根.
(1)求 m 的取值范围;
(2)写出一个满足条件的 m 的值,并求此时方程的根.
3
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
19.已知一次函数 1 = 2 + 的图象与反比例函数 2 = ( > 0)的图象交于 A,B 两点.
(1)当点 A 的坐标为(2,1)时.
①求 m,k 的值;
②当 > 2时, 1_____ 2(填“>”,“=”或“<”).
(2)将一次函数 1 = 2 + 的图象沿 y 轴向下平移 4 个单位长度后,使得点 A,B 关于原点对称,
求 m 的值 . y
6
5
4
3
2
1
-6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6 x-1
-2
-3
-4
-5
-6
20.已知抛物线 = 2 + + + 2( ≠ 0)与 x 轴交于点 A( 1,0),点 B( 2,0)(点 A 在点 B
的左侧),抛物线的对称轴为直线 = 1.
(1)若点 A 的坐标为( 3,0),求
①抛物线的表达式
②点 B 的坐标 ;
(2)C 是第三象限的点,且点 C 的横坐标为 2,若抛物线恰好经过点 C,直接写出 x2 的取值范围.
21.两个质地均匀的正方体 M 和 N,正方体 M 的六个面分别标有数字“0”“1”“2”“3”“4”“5”;正方体 N
的六个面分别标有数字“0”“1”“2”“6”“7”“8”.掷小正方体后,观察朝上一面的数字.如果先掷一次
正方体 M,再掷一次正方体 N 得到两个数字,如先后掷到“0”和“1”记为 01,可表示某月的 01 日:
先后掷到“5”和“8”记为 58,不能表示某月的日期.求先后各掷一次正方体 M 和正方体 N,得到的
两个数字能组成一月的一个日期的概率.
4
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
22.如图, 是☉ 外一点, 与☉ 相切,切点为 . 画出☉ 的另一条切线 ,切点为 .
小云的画法是:
①连接 ,过点 画出 的垂线交☉ 于点 ;
②画出直线 . P
直线 即为所求.
(1)根据小云的画法,补全图形;
(2)完成下面的证明. A
证明:连接 , . O
∵ = , ⊥ ,
∴ 垂直平分 ,∠ = ∠ .
∴ = ① .
∴∠ = ② .
∴∠ = ∠ .
∵ 是☉ 的切线, 为切点,
∴ ⊥ .
∴∠ = 90°.
∴∠ = 90°.
∴ ⊥ 于点 .
∵ 是☉ 的半径,
∴ 是☉ 的切线( ③ )(填推理的依据).
23. 在△ABC 中,∠ACB=90°,AC<BC,点 D 在 AC 的延长线上,点 E 在 BC 边上,且 BE=AD.
(1)如图 1,连接 AE,DE,当∠AEB=110°时,求∠DAE 的度数;
(2)在图 2 中,将线段 AE 绕点 E 顺时针旋转 90°得到线段 EF,连接 BF,DE.
①依题意补全图形;
②求证:BF=DE.
图 1 图 2
5
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
24.如图,AB 为⊙O 的直径,CD 为弦,CD⊥AB 于点 E,连接 DO 并延长交⊙O 于点 F,连接 AF
交 CD 于点 G,CG=AG,连接 AC.
C F
(1)求证:AC∥DF;
(2)若 AB=12,求 AC 和 GD 的长.
G
A E O B
D
25.由于惯性的作用,行使中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹
车距离”.某公司设计了一款新型汽车,现在对它的刹车性能(车速不超过 150km/ )进行测试,
测得数据如下表:
车速 (km/ ) 0 30 60 90 120 150
刹车距离 ( ) 0 7.8 19.2 34.2 52.8 75
(1)以车速 为横坐标,刹车距离 为纵坐标,在坐标 s ( m ) s
80
系中描出表中各组数值所对应的点,并用平滑曲线连
70
接这些点;
60
(2)由图表中的信息可知: 50
40
①该型汽车车速越大,刹车距离越_________(填“大”
30
或“小”);
20
②若该型汽车某次测试的刹车距离为 40 m,估计该车 10
的速度约为__________ km/h; O 30 60 90 120 150 v( km/h )
(3)若该路段实际行车的最高限速为 120 km/h,要求
该型汽车的安全车距要大于最高限速时刹车距离的 3 倍,则安全车距应超过 ________m.
6
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
7
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
28.如图,在平面直角坐标系 xOy 中,已知点 M(0,t),N(0,t+2),给出如下定义:
若∠MPN=30°,则称点 P 为线段 MN 的“亲近点”.
(1)当 t=0 时,
①在点 ,B(3,2), ,D(﹣1,﹣3)中,线段 MN 的“亲近点”
是 ;
②点 P 在直线 y=1 上,若点 P 为线段 MN 的“亲近点”,则点 P 的坐标为 ;
(2)若直线 上总存在线段 MN 的“亲近点”,则 t 的取值范围是 .
8
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
班级: 姓名: 成绩:
一、选择题(本题共 16 分,每题 2 分)第 1 - 8 题均有四个选项,符合题意的选项只有一个.
1. 抛物线 = ( + 2)2 1的对称轴是
A. = 1 B. = 1 C. = 2 D. = 2
2.下面的图形中,既是轴对称图形又是中心对称图形的是
A. B. C. D.
3.在下列事件中,随机事件是
A.投掷一枚质地均匀的骰子,向上一面的点数不超过 6
B.从装满红球的袋子中随机摸出一个球,是白球
C.通常情况下,自来水在 10℃结冰
D.投掷一枚质地均匀的骰子,向上一面的点数为 2
4. 如图,AB 是⊙O 的直径,C,D 是⊙O 上的两点.若∠CAB=65°,则∠ADC 的度数为
A.65° B.35°
C.32.5° D.25°
5.如果甲、乙、丙三位同学随机站成一排,那么甲站在中间的概率是
1 1 2 1
A. B. C. D.
2 6 3 3
6.平面直角坐标系 xOy 中,若点 ( 1, 2)和 ( 2, 4)在反比例函数 = ( > 0)图象上,则下列关系式
正确的是
A. 1 > 2 > 0 B. 2 > 1 > 0 C. 1 < 2 < 0 D. 2 < 1 < 0
7.某商店在节日期间开展优惠促销活动:购买原价超过 200 元的商品,超.过.200
元的部分可以享受打折优惠.若购买商品的实际付款金额 y(单位:元)与商
品原价 x(单位:元)的函数关系的图象如图所示,则超.过.200 元的部分可以
享受的优惠是( )
A.打八折 B.打七折 C.打六折 D.打五折
1
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
8.如图,正方形 ABCD 的边长是 4,E 是 AB 上一点,F 是 AD 延长线上的一
A D F
点,且 BE=DF,四边形 AEGF 是矩形,设 BE 的长为 x,AE 的长为 y,
矩形 AEGF 的面积为 S,则 y 与 x,S 与 x 满足的函数关系分别是 E
G
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系 B C
C.一次函数关系,反比例函数关系 D.反比例函数关系,一次函数关系
二、填空题(本题共 16 分,每题 2 分)
9.点 M(2,-4),N 关于原点对称,则点 N 的坐标是 .
10.已知⊙O 的半径为 6,若点 P 在⊙O 外,则 OP 6(填“>”“=”或“<”).
11. 如果一个圆锥的母线长为 4,底面半径为 1,那么这个圆锥的侧面积为 .
12.“圆”是中国文化的一个重要精神元素,在中式建筑
中有着广泛的应用,例如古典园林中的门洞,如图,
某地园林中的一个圆弧形门洞的高为 2.5m,地面入口
宽为 1m,则该门洞的半径为__________m.
13.为了解某小麦品种的发芽率,某农业合作小组在相同条件下对该小麦做发芽试验,试验数据如下
表:
种子个数 n 5 50 100 200 500 1 000 2 000 3 000
发芽种子个数 m 4 44 92 189 476 951 1 898 2 851
发芽种子频率 0.800 0.880 0.920 0.945 0.952 0.951 0.949 0.950
(1)估计该品种小麦在相同条件下发芽的概率为 (结果保留两位小数);
(2)若在相同条件下播种该品种小麦种子 10 000 个,则约有 个能发芽.
14.中国邮政集团公司曾发行《二十四节气》特殊版式小全张(图 1),其中的 24 枚邮票大小相同,
上面绘制了代表二十四节气风貌的图案,这 24 枚邮票组成了一个圆环,传达了四季周而复始、气
韵流动的理念和中国传统文化中圆满、圆融的概念.以“大雪”节气单枚邮票为例(图 2),该邮票
的“上圆弧”的长为 l,“直边长”为 d,“下圆弧”的长为 x,则 x= (用含 l,
d 的式子表示).
2
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
5
15.如图 1,一名男生推铅球,铅球的运动路线近似是抛物线的一部分.铅球出手位置的高度为 m,
3
当铅球行进的水平距离为 4 m 时,高度达到最大值 3 m. 铅球的行进高度 y(单位:m)与水平距离 x
(单位:m)之间的关系满足二次函数. 若以最高点为原点,过原点的水平直线为 x 轴,建立如图 2
1
所示的平面直角坐标系 xOy,则该二次函数的解析式为 = 2.若以过出手点且与地面垂直的直线
12
为 y 轴,y 轴与地面的交点为原点,建立如图 3 所示的平面直角坐标系 xOy,则该二次函数的解析式
为 .
16.在平面直角坐标系 xOy 中,点 A 的坐标为(1,0).P 是第一象限内任意一点,连接 PO,PA.若
∠POA= m°,∠PAO= n°,则我们把 P(m°,n°)叫做点 P 的“双角坐标”.例如,点(1,1)的“双
角坐标”为(45°,90°).
1 3
( √1)点( , )的“双角坐标”为______________;
2 2
1
(2)若点 P 到 x 轴的距离为 ,则 m+n 的最小值为__________.
2
三、解答题(共 68 分,第 17-22 题,每题 5 分,第 23-26 题,每题 6 分,27-28 题,每题 7 分)解答应写
出文字说明、演算步骤或证明过程.
4 3 ≥ 3( 1),
17.解不等式组:{2 +6
< .
5
18.关于 x 的一元二次方程 2 (2 + 1) + 2 = 0有两个实数根.
(1)求 m 的取值范围;
(2)写出一个满足条件的 m 的值,并求此时方程的根.
3
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
19.已知一次函数 1 = 2 + 的图象与反比例函数 2 = ( > 0)的图象交于 A,B 两点.
(1)当点 A 的坐标为(2,1)时.
①求 m,k 的值;
②当 > 2时, 1_____ 2(填“>”,“=”或“<”).
(2)将一次函数 1 = 2 + 的图象沿 y 轴向下平移 4 个单位长度后,使得点 A,B 关于原点对称,
求 m 的值 . y
6
5
4
3
2
1
-6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6 x-1
-2
-3
-4
-5
-6
20.已知抛物线 = 2 + + + 2( ≠ 0)与 x 轴交于点 A( 1,0),点 B( 2,0)(点 A 在点 B
的左侧),抛物线的对称轴为直线 = 1.
(1)若点 A 的坐标为( 3,0),求
①抛物线的表达式
②点 B 的坐标 ;
(2)C 是第三象限的点,且点 C 的横坐标为 2,若抛物线恰好经过点 C,直接写出 x2 的取值范围.
21.两个质地均匀的正方体 M 和 N,正方体 M 的六个面分别标有数字“0”“1”“2”“3”“4”“5”;正方体 N
的六个面分别标有数字“0”“1”“2”“6”“7”“8”.掷小正方体后,观察朝上一面的数字.如果先掷一次
正方体 M,再掷一次正方体 N 得到两个数字,如先后掷到“0”和“1”记为 01,可表示某月的 01 日:
先后掷到“5”和“8”记为 58,不能表示某月的日期.求先后各掷一次正方体 M 和正方体 N,得到的
两个数字能组成一月的一个日期的概率.
4
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
22.如图, 是☉ 外一点, 与☉ 相切,切点为 . 画出☉ 的另一条切线 ,切点为 .
小云的画法是:
①连接 ,过点 画出 的垂线交☉ 于点 ;
②画出直线 . P
直线 即为所求.
(1)根据小云的画法,补全图形;
(2)完成下面的证明. A
证明:连接 , . O
∵ = , ⊥ ,
∴ 垂直平分 ,∠ = ∠ .
∴ = ① .
∴∠ = ② .
∴∠ = ∠ .
∵ 是☉ 的切线, 为切点,
∴ ⊥ .
∴∠ = 90°.
∴∠ = 90°.
∴ ⊥ 于点 .
∵ 是☉ 的半径,
∴ 是☉ 的切线( ③ )(填推理的依据).
23. 在△ABC 中,∠ACB=90°,AC<BC,点 D 在 AC 的延长线上,点 E 在 BC 边上,且 BE=AD.
(1)如图 1,连接 AE,DE,当∠AEB=110°时,求∠DAE 的度数;
(2)在图 2 中,将线段 AE 绕点 E 顺时针旋转 90°得到线段 EF,连接 BF,DE.
①依题意补全图形;
②求证:BF=DE.
图 1 图 2
5
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
24.如图,AB 为⊙O 的直径,CD 为弦,CD⊥AB 于点 E,连接 DO 并延长交⊙O 于点 F,连接 AF
交 CD 于点 G,CG=AG,连接 AC.
C F
(1)求证:AC∥DF;
(2)若 AB=12,求 AC 和 GD 的长.
G
A E O B
D
25.由于惯性的作用,行使中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹
车距离”.某公司设计了一款新型汽车,现在对它的刹车性能(车速不超过 150km/ )进行测试,
测得数据如下表:
车速 (km/ ) 0 30 60 90 120 150
刹车距离 ( ) 0 7.8 19.2 34.2 52.8 75
(1)以车速 为横坐标,刹车距离 为纵坐标,在坐标 s ( m ) s
80
系中描出表中各组数值所对应的点,并用平滑曲线连
70
接这些点;
60
(2)由图表中的信息可知: 50
40
①该型汽车车速越大,刹车距离越_________(填“大”
30
或“小”);
20
②若该型汽车某次测试的刹车距离为 40 m,估计该车 10
的速度约为__________ km/h; O 30 60 90 120 150 v( km/h )
(3)若该路段实际行车的最高限速为 120 km/h,要求
该型汽车的安全车距要大于最高限速时刹车距离的 3 倍,则安全车距应超过 ________m.
6
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
7
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
28.如图,在平面直角坐标系 xOy 中,已知点 M(0,t),N(0,t+2),给出如下定义:
若∠MPN=30°,则称点 P 为线段 MN 的“亲近点”.
(1)当 t=0 时,
①在点 ,B(3,2), ,D(﹣1,﹣3)中,线段 MN 的“亲近点”
是 ;
②点 P 在直线 y=1 上,若点 P 为线段 MN 的“亲近点”,则点 P 的坐标为 ;
(2)若直线 上总存在线段 MN 的“亲近点”,则 t 的取值范围是 .
8
{#{QQABBYQQogCgAABAAQgCEwGYCgCQkBAACAoGBEAAsAABiBNABAA=}#}
同课章节目录
