2023-2024学年数学八年级分式单元测试试题(华东师大版)(提升卷一)含解析
文档属性
| 名称 | 2023-2024学年数学八年级分式单元测试试题(华东师大版)(提升卷一)含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 898.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 19:49:22 | ||
图片预览


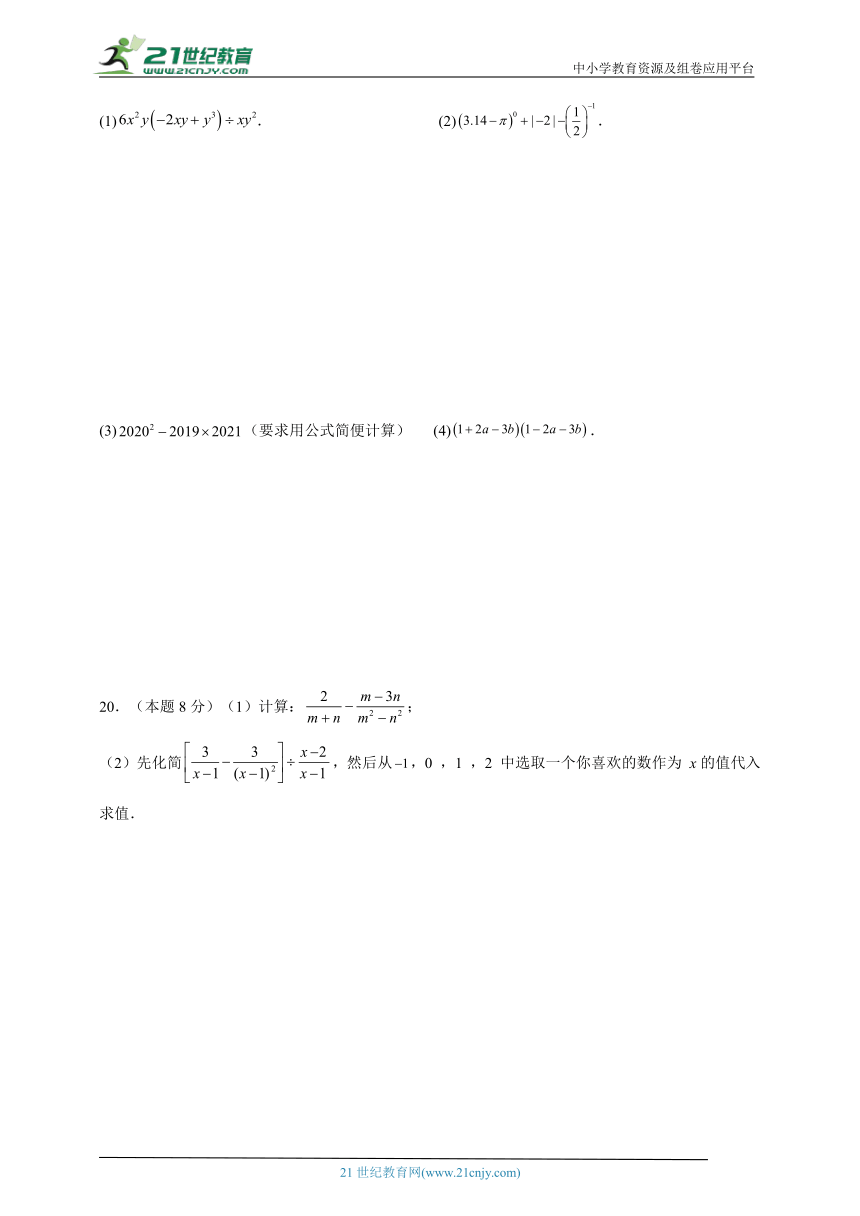

文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学八年级分式(华东师大版)
单元测试 (提升卷一) 含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)《四元玉鉴》是我国古代数学重要著作之一,为元代数学家朱世杰所著,该著作记载了“买椽多少”问题(椽—装于屋顶以支持屋顶材料的木杆).
设这批椽有x株,则符合题意的方程是( )
A. B. C. D.
2.(本题3分)分式方程的解是( )
A. B. C. D.
3.(本题3分)“退耕还林还草”是我国西部地区实施的一项重要生态工程,某地规划退耕面积共69000公顷,退耕还林与退耕还草的面积比为,设退耕还林的面积为x公顷,下列所列方程哪一个是不正确的?( )
A. B.
C. D.
4.(本题3分)截至2023年12月31日,中国内地累计有59个城市投运城轨交通线路公里,中国地铁的发展速度之快,让世界相形见绌.小明和小强分别从A地和B地出发赶往机场乘坐飞机,出行方式、路径及路程如下表所示:
出行方式 路径 路程
地铁 A地机场 全程约43公里
公交 B地机场 全程约54公里
由于地面交通拥堵,地铁的平均速度约为公交平均速度的两倍,于是小明比小强少用了半小时到达机场.若设公交的平均速度为公里/时,根据题意可列方程( )
A. B.
C. D.
5.(本题3分)若,在如图的数轴上标注了四段,则表示的点落在( )
A.段① B.段② C.段③ D.段④
6.(本题3分)下列计算正确的是( )
A. B. C. D.
7.(本题3分)若分式有意义,下列说法错误的是( ).
A.当时,分式的值为正数 B.当时,分式无意义
C.当时,分式的值为0 D.当时,分式的值为1
8.(本题3分)如果,那么代数的值为( )
A. B. C. D.
9.(本题3分)下列各式中,计算正确的是( )
A.
B.
C.
D.
10.(本题3分)张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子()的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为,则另一边长是,矩形的周长是;当矩形成为正方形时,就有(),解得,这时矩形的周长最小,因此()的最小值是.模仿张华的推导,你求得式子()的最小值是( )
A. B. C. D.
评卷人得分
二、填空题(共24分)
11.(本题3分)若,则等于 .
12.(本题3分)若分式方程的解是正数,则的取值范围为 .
13.(本题3分)若分式的值为0,则 .
14.(本题3分)关于的分式方程无解,则的值为 .
15.(本题3分)已知关于的分式方程的解为非负数,则正整数的值为 .
16.(本题3分)在读书活动中,某同学对甲、乙两个班学生的读书情况进行了统计:甲班学生人数比乙班学生人数多2人,甲班学生读书256本,乙班学生读书180本,乙班平均每人读书的本数是甲班平均每人读书的本数,求甲乙两班各有多少人?设乙班有人,依题意,可列方程为 .
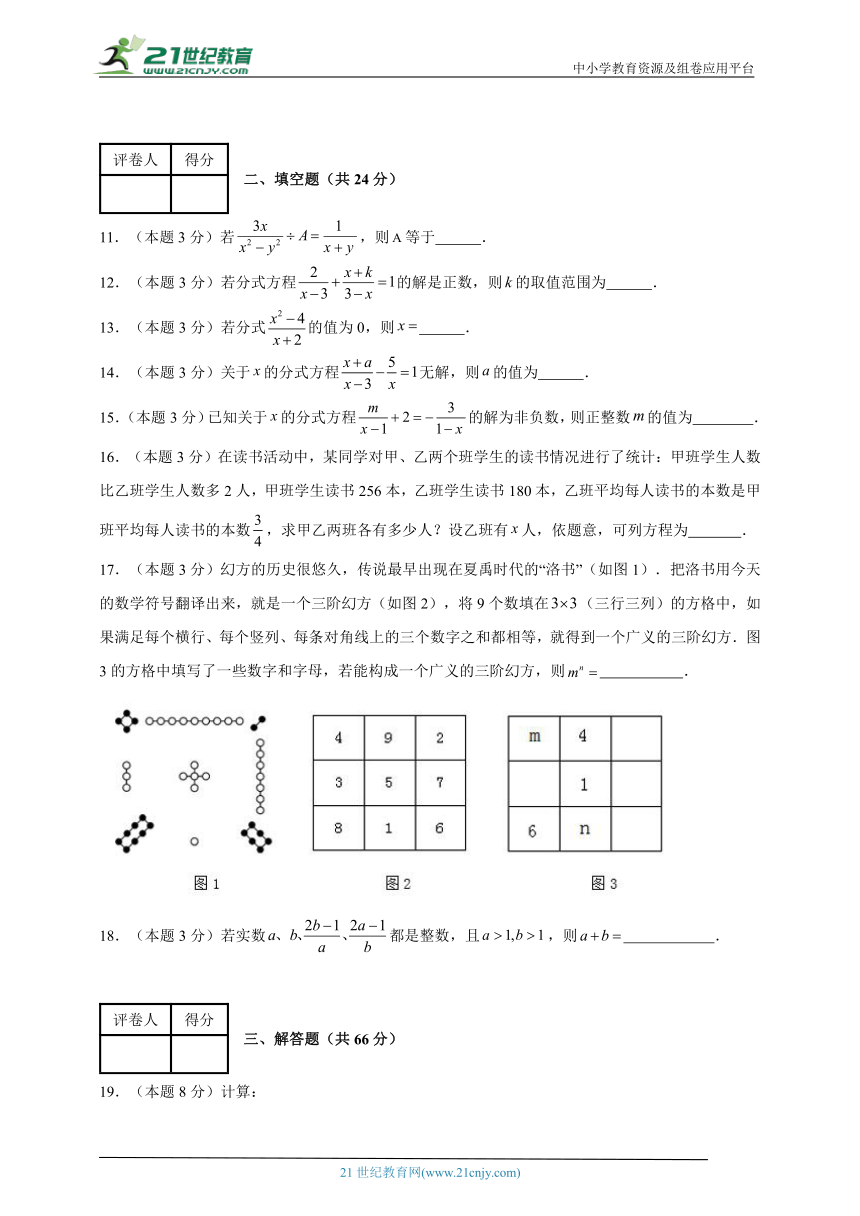
17.(本题3分)幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”(如图1).把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图2),将9个数填在(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图3的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则 .
18.(本题3分)若实数都是整数,且,则 .
评卷人得分
三、解答题(共66分)
19.(本题8分)计算:
(1). (2).
(3)(要求用公式简便计算) (4).
20.(本题8分)(1)计算:;
(2)先化简,然后从,0 ,1 ,2 中选取一个你喜欢的数作为 x的值代入求值.
21.(本题8分)甲乙两组要加工一批零件,乙组每小时加工的零件数比甲的 2 倍少 200 个, 甲组加工2000个零件与乙组加工 3000个零件时间相同.
(1)甲乙两组每小时各加工多少个零件?
(2)由于突发情况,甲乙两组需要加急完成13600个零件的加工任务. 因此,甲组每小时比之前多加工 60个零件,乙组每小时加工的零件个数也比之前增加了,即便如此,也需要m个小时才能完成任务,求 m的值.
22.(本题10分)先化简,再求值:,其中.
23.(本题10分)(1)解方程: ;
(2)先化简,再求值:,其中.
24.(本题10分)列分式方程解应用题:某超市的一种瓶装饮料每箱售价为36元,五一期间对该瓶装饮料进行促销活动,买一箱送两瓶,这相当于每瓶按原价九折销售,求这家超市销售的这种饮料每箱多少瓶?
25.(本题12分)阅读以下材料:
已知两个两位数,将它们各自的十位数字和个位数字交换位置后,得到两个与原两个两位数均不同的新数,若这两个两位数的和与交换位置后两个新两位数的和相等,则称这样的两个两位数为“臻美数对”,例如,所以与、与都是“臻美数对”.
解决如下问题:
(1)请判断与是否是“臻美数对”?并说明理由;
(2)为探究“臻美数对”的本质,可设“臻美数对”中一个数的十位数字为a,个位数字为b,且;另一个数的十位数字为c,个位数字为d,且,试说明之间满足怎样的数量关系,并证明“臻美数对”的两数和是的倍数;
(3)若有一个两位数,十位数字为,个位数字为;另一个两位数,十位数字为,个位数字为,假设这两个数为“臻美数对”,求出这两个两位数.
参考答案:
1.D
【分析】本题考查根据实际问题列分式方程.解题的关键是找准等量关系,正确的列出方程.根据如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,列出方程即可.
【详解】解:∵如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,
∴可列方程为:;
故选:D.
2.D
【分析】本题考查解分式方程,先将分式方程转化为整式方程求解,最后要注意验根.
先将方程转化为整式方程求解,再检验即可.
【详解】解:
,
检验:当时,,
∴原分式方程的解为,
故选:D.
3.B
【分析】本题主要考查分式方程的应用,根据退耕还林与退耕还草的面积比为列出方程,合理变形是解决本题的关键.根据等量关系:退耕还林的面积:退耕还草的面积,列出方程即可.
【详解】解:设退耕还林的面积为x公顷,则退耕还草的面积为公顷,根据题意得:
或或或,因此错误,故B符合题意.
故选:B.
4.B
【分析】本题主要考查了列分式方程,正确理解题意找到等量关系是解题的关键.设公交的平均速度为x公里/时,则地铁的平均速度为2x公里/时,然后根据小贝比小京少用了半小时到达机场,列出方程即可.
【详解】解:设公交的平均速度为x公里/时,则地铁的平均速度为2x公里/时,
由题意得:,
故选B.
5.D
【分析】本题考查分式的化简求值,实数与数轴,分式的分子、分母先因式分解,再约去公因式,把分式化为最简分式,最后将代入化简的式子即可求值.
【详解】解:原式=,
当时,
原式=,
故选:D
6.C
【分析】根据零指数幂运算法则、负整数指数幂运算法则、幂的乘方运算法则以及同底数幂的除法运算法则,逐项分析判断即可.
【详解】解:A、当时,可有,故本选项运算不正确,不符合题意;
B、若,则有,整理可得,而,故本选项运算不正确,不符合题意;
C、,运算正确,符合题意;
D、,故本选项运算不正确,不符合题意.
故选:C.
【点睛】本题主要考查了零指数幂运算、负整数指数幂运算、幂的乘方运算以及同底数幂的除法运算,熟练掌握相关运算法则是解题关键.
7.A
【分析】本题考查了分式的值,分式的值为零,分式有意义的条件,分式的值为正,熟练掌握这些知识是解题的关键.
根据分式的值为0的条件,分式有意义的条件,分式的值为正,分式的值,逐项判断即可.
【详解】解:A、当时,分母,但的值可能是正数也可能是负数,根据“两数相除同号得正,异号得负”可判定分式的值可能是正数,也可能是负数,还可能是0,故此选项错误,符合题意;
B、当时,分母,所以当时,分式无意义,故此选项正确,不符合题意;
C、当时,分母,分子,当时,分式的值为0,故此选项正确,不符合题意;
D、当时,分母,,当时,分式的值为1,故此选项正确,不符合题意.
故选:A.
8.B
【分析】本题考查分式的化简求值,利用分式化简法则将化简,再把代入即可,熟练掌握分式混合运算的法则是解题的关键.
【详解】解:,
,
,
,
,
原式,
故选:B.
9.D
【分析】本题主要考查、多项式除以单项式、多项式乘以多项式、分式的加减运算法则及平方差公式.分别根据多项式除以单项式、多项式乘以多项式、分式的加减运算法则及平方差公式逐一计算可得.
【详解】A、,此选项计算错误;
B、,此选项计算错误;
C、,此选项计算错误;
D、,此选项计算正确;
故选:D.
10.A
【分析】本题考查了分式的混合运算,理解并应用题目中的计算方法是解题的关键.
根据题目中的计算方法进行求解即可.
【详解】解:∵,
∴在原式中分母分子同除以,
即;
在面积是的矩形中设矩形的一边长为,则另一边长是,
矩形的周长是;
当矩形成为正方形时,就有(),
解得:,
这时矩形的周长最小,
因此()的最小值是.
故选:A.
11.
【分析】本题主要考查了分式的除法计算,根据分式的除法计算法则求出的结果即可得到答案.
【详解】解:∵,
∴
,
故答案为:.
12.且
【分析】本题主要考查了根据分式方程解的情况求参数,先解分式方程得到,再根据分式方程的解为正数以及方程不能有增根得到,解之即可得到答案.
【详解】解:
去分母得:,
去括号得:,
移项得:,
合并同类项得:,
系数化为1得:,
∵分式方程的解是正数,
∴,
∴且,
故答案为:且.
13.
【分析】本题考查分式的值为0的条件.分式的值是0的条件是,分子为0,分母不为0,进行求解即可.
【详解】解:由题意得,,
,,
,
即当时,分式的值是
故答案为:
14.2或/或2
【分析】本题考查了分式方程无解问题,分两种情况分别计算:当时,该整式方程无解,当时,由分式方程无解得到增根或,代入整式方程计算即可;熟练掌握分式方程无解的条件是:去分母后所得整式方程无解或解这个整式方程得到的解使原方程的分母等于零.
【详解】解:,
去分母得:,
整理得:,
当时,该整式方程无解,此时,
当时,要是原方程无解,则,即或,
把代入整式方程,的值不存在,
把代入整式方程,得,
综上所述,当或时,关于的分式方程无解,
故答案为:2或.
15.5、4、2、1
【分析】本题考查了分式方程的解,解一元一次不等式组.考虑到分式方程有可能产生增根的情形是解题的关键.利用解分式方程的一般步骤求得分式方程的解,由题意得到不等式;分式方程有可能产生使分母为0的增根,所以原方程的解不等于1,由以上两个条件即可得出答案.
【详解】解:去分母,得:
,
移项,合并同类项,得:
.
∵解为非负数,
∴,
∴.
∵原分式方程有可能产生增根,
∴,
∴,
∴正整数的值为5、4、2、1.
故答案为:5、4、2、1.
16.
【分析】本题考查分式方程的实际应用.根据乙班平均每人读书的本数是甲班平均每人读书的本数,列出分式方程即可.
【详解】解:设乙班有人,则甲班有人,由题意,得:;
故答案为:.
17.
【分析】本题考查了一元一次方程的应用、负指数幂计算及代数式求值,由题意可得到关于的两个方程,解方程即可求出的值,再把的值代入计算即可求解,根据题意,正确列出一元一次方程是解题的关键.
【详解】解:设右上角数字为x,右下角数字为y,
由题意可得,,,
解得,,
∴,
故选:.
18.8
【分析】本题考查分式的方程的应用,熟练解分式方程是正确解决本题的关键.
利用已知条件建立分式方程,并全面地进行分类讨论即可得出.
【详解】解:当时,,
,
不是整数,与题设矛盾,
,
令,
由题设m、n为正整数,
设,
由①得,
代入②,整理得,
是正整数,
或2或3,
又,
或,
当时,
由①②解得,(不合题意,舍去),
当时,
由①②解得,,
.
故答案为:8.
19.(1)
(2)1
(3)1
(4)
【分析】本题考查了整式的混合运算,绝对值,零指数幂,负整数指数幂,完全平方公式,平方差公式,准确熟练地进行计算是解题的关键.
(1)按照从左到右的顺序进行计算,即可解答;
(2)先化简各式,然后再进行计算即可解答;
(3)利用平方差公式进行计算,即可解答;
(4)利用完全平方公式,平方差公式进行计算,即可解答.
【详解】(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
.
20.(1);(2);时,原式
【分析】本题主要考查了分式化简求值,解题的关键是熟练掌握分式混合运算法则,准确计算.
(1)根据分式加减运算法则进行计算即可;
(2)先根据分式混合运算法则进行化简,然后再代入求值即可.
【详解】解:(1)
;
(2)
,
∵,,
∴,2,
把代入得:原式.
21.(1)甲每小时加工的零件数为个,乙组每小时加工的零件数为个
(2)m的值为10
【分析】本题考查了分式方程的应用,一元一次方程的应用,根据题意列出方程是解题的关键.
(1)设甲每小时加工的零件数为个,则乙组每小时加工的零件数为个,根据题意列出分式方程,解方程即可求解;
(2)分别表示出甲、乙每小时的加工的零件数量,根据题意,列出一元一次方程即可求解.
【详解】(1)解:设甲每小时加工的零件数为个,则乙组每小时加工的零件数为个,根据题意得:
,
解得:,
经检验,是原方程的解,
∴(个);
答:甲每小时加工的零件数为个,乙组每小时加工的零件数为个;
(2)解:依题意得:,
解得:,
答:m的值为10.
22.,
【分析】本题考查分式的化简求值,解题关键是掌握分式的混合运算法则.先根据分式的混合运算将式子化简,再将计算出的x的值代入计算即可.
【详解】解:原式
,
,
,
当时,原式.
23.(1)原方程无解;(2),当时,原式
【分析】本题主要考查了解分式方程,分式的化简求值:
(1)按照去分母,移项,合并同类项的步骤解方程,然后检验即可得到答案;
(2)先根据分式的混合计算法则化简,然后代值计算即可得到答案.
【详解】解:(1)
去分母得:,
移项得:,
合并同类项得:,
检验,当时,,
∴是原方程的增根,
∴原方程无解;
(2)
,
当时,原式=.
24.这家超市销售这种饮料每箱18瓶
【分析】本题考查了分式方程的应用,设品牌饮料每箱瓶,根据“买一箱送两瓶,这相当于每瓶按原价九折销售”列方程求解即可,根据题意找出等量关系是解题的关键.
【详解】解:设品牌饮料每箱瓶,则依据题意得:
解得:
经检验:是原方程的解
答:这家超市销售这种饮料每箱18瓶.
25.(1)是,理由见详解
(2),理由见详解;证明见详解
(3)
【分析】本题考查了整式的加减、分式的运算和分式方程,读懂题意是解题关键.
(1)根据“臻美数对”的定义即可求解;
(2)结合“臻美数对”的定义及整式的加减即可求解;
(3)由(2)的结合分式的加减即可求解.
【详解】(1)解:将与各自的十位数字和个位数字交换位置可得:,
,
与是“臻美数对;
(2),理由如下:
由题意得:
,
移项合并同类项可得:
,
左右两边同时除以9可得:
;
两“臻美数对”的和为:
两“臻美数对”的和是的倍数;
(3)这两个数为“臻美数对”,
即
解得:,
,;
,,
这两个数分别为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学八年级分式(华东师大版)
单元测试 (提升卷一) 含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)《四元玉鉴》是我国古代数学重要著作之一,为元代数学家朱世杰所著,该著作记载了“买椽多少”问题(椽—装于屋顶以支持屋顶材料的木杆).
设这批椽有x株,则符合题意的方程是( )
A. B. C. D.
2.(本题3分)分式方程的解是( )
A. B. C. D.
3.(本题3分)“退耕还林还草”是我国西部地区实施的一项重要生态工程,某地规划退耕面积共69000公顷,退耕还林与退耕还草的面积比为,设退耕还林的面积为x公顷,下列所列方程哪一个是不正确的?( )
A. B.
C. D.
4.(本题3分)截至2023年12月31日,中国内地累计有59个城市投运城轨交通线路公里,中国地铁的发展速度之快,让世界相形见绌.小明和小强分别从A地和B地出发赶往机场乘坐飞机,出行方式、路径及路程如下表所示:
出行方式 路径 路程
地铁 A地机场 全程约43公里
公交 B地机场 全程约54公里
由于地面交通拥堵,地铁的平均速度约为公交平均速度的两倍,于是小明比小强少用了半小时到达机场.若设公交的平均速度为公里/时,根据题意可列方程( )
A. B.
C. D.
5.(本题3分)若,在如图的数轴上标注了四段,则表示的点落在( )
A.段① B.段② C.段③ D.段④
6.(本题3分)下列计算正确的是( )
A. B. C. D.
7.(本题3分)若分式有意义,下列说法错误的是( ).
A.当时,分式的值为正数 B.当时,分式无意义
C.当时,分式的值为0 D.当时,分式的值为1
8.(本题3分)如果,那么代数的值为( )
A. B. C. D.
9.(本题3分)下列各式中,计算正确的是( )
A.
B.
C.
D.
10.(本题3分)张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子()的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为,则另一边长是,矩形的周长是;当矩形成为正方形时,就有(),解得,这时矩形的周长最小,因此()的最小值是.模仿张华的推导,你求得式子()的最小值是( )
A. B. C. D.
评卷人得分
二、填空题(共24分)
11.(本题3分)若,则等于 .
12.(本题3分)若分式方程的解是正数,则的取值范围为 .
13.(本题3分)若分式的值为0,则 .
14.(本题3分)关于的分式方程无解,则的值为 .
15.(本题3分)已知关于的分式方程的解为非负数,则正整数的值为 .
16.(本题3分)在读书活动中,某同学对甲、乙两个班学生的读书情况进行了统计:甲班学生人数比乙班学生人数多2人,甲班学生读书256本,乙班学生读书180本,乙班平均每人读书的本数是甲班平均每人读书的本数,求甲乙两班各有多少人?设乙班有人,依题意,可列方程为 .
17.(本题3分)幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”(如图1).把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图2),将9个数填在(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图3的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则 .
18.(本题3分)若实数都是整数,且,则 .
评卷人得分
三、解答题(共66分)
19.(本题8分)计算:
(1). (2).
(3)(要求用公式简便计算) (4).
20.(本题8分)(1)计算:;
(2)先化简,然后从,0 ,1 ,2 中选取一个你喜欢的数作为 x的值代入求值.
21.(本题8分)甲乙两组要加工一批零件,乙组每小时加工的零件数比甲的 2 倍少 200 个, 甲组加工2000个零件与乙组加工 3000个零件时间相同.
(1)甲乙两组每小时各加工多少个零件?
(2)由于突发情况,甲乙两组需要加急完成13600个零件的加工任务. 因此,甲组每小时比之前多加工 60个零件,乙组每小时加工的零件个数也比之前增加了,即便如此,也需要m个小时才能完成任务,求 m的值.
22.(本题10分)先化简,再求值:,其中.
23.(本题10分)(1)解方程: ;
(2)先化简,再求值:,其中.
24.(本题10分)列分式方程解应用题:某超市的一种瓶装饮料每箱售价为36元,五一期间对该瓶装饮料进行促销活动,买一箱送两瓶,这相当于每瓶按原价九折销售,求这家超市销售的这种饮料每箱多少瓶?
25.(本题12分)阅读以下材料:
已知两个两位数,将它们各自的十位数字和个位数字交换位置后,得到两个与原两个两位数均不同的新数,若这两个两位数的和与交换位置后两个新两位数的和相等,则称这样的两个两位数为“臻美数对”,例如,所以与、与都是“臻美数对”.
解决如下问题:
(1)请判断与是否是“臻美数对”?并说明理由;
(2)为探究“臻美数对”的本质,可设“臻美数对”中一个数的十位数字为a,个位数字为b,且;另一个数的十位数字为c,个位数字为d,且,试说明之间满足怎样的数量关系,并证明“臻美数对”的两数和是的倍数;
(3)若有一个两位数,十位数字为,个位数字为;另一个两位数,十位数字为,个位数字为,假设这两个数为“臻美数对”,求出这两个两位数.
参考答案:
1.D
【分析】本题考查根据实际问题列分式方程.解题的关键是找准等量关系,正确的列出方程.根据如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,列出方程即可.
【详解】解:∵如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,
∴可列方程为:;
故选:D.
2.D
【分析】本题考查解分式方程,先将分式方程转化为整式方程求解,最后要注意验根.
先将方程转化为整式方程求解,再检验即可.
【详解】解:
,
检验:当时,,
∴原分式方程的解为,
故选:D.
3.B
【分析】本题主要考查分式方程的应用,根据退耕还林与退耕还草的面积比为列出方程,合理变形是解决本题的关键.根据等量关系:退耕还林的面积:退耕还草的面积,列出方程即可.
【详解】解:设退耕还林的面积为x公顷,则退耕还草的面积为公顷,根据题意得:
或或或,因此错误,故B符合题意.
故选:B.
4.B
【分析】本题主要考查了列分式方程,正确理解题意找到等量关系是解题的关键.设公交的平均速度为x公里/时,则地铁的平均速度为2x公里/时,然后根据小贝比小京少用了半小时到达机场,列出方程即可.
【详解】解:设公交的平均速度为x公里/时,则地铁的平均速度为2x公里/时,
由题意得:,
故选B.
5.D
【分析】本题考查分式的化简求值,实数与数轴,分式的分子、分母先因式分解,再约去公因式,把分式化为最简分式,最后将代入化简的式子即可求值.
【详解】解:原式=,
当时,
原式=,
故选:D
6.C
【分析】根据零指数幂运算法则、负整数指数幂运算法则、幂的乘方运算法则以及同底数幂的除法运算法则,逐项分析判断即可.
【详解】解:A、当时,可有,故本选项运算不正确,不符合题意;
B、若,则有,整理可得,而,故本选项运算不正确,不符合题意;
C、,运算正确,符合题意;
D、,故本选项运算不正确,不符合题意.
故选:C.
【点睛】本题主要考查了零指数幂运算、负整数指数幂运算、幂的乘方运算以及同底数幂的除法运算,熟练掌握相关运算法则是解题关键.
7.A
【分析】本题考查了分式的值,分式的值为零,分式有意义的条件,分式的值为正,熟练掌握这些知识是解题的关键.
根据分式的值为0的条件,分式有意义的条件,分式的值为正,分式的值,逐项判断即可.
【详解】解:A、当时,分母,但的值可能是正数也可能是负数,根据“两数相除同号得正,异号得负”可判定分式的值可能是正数,也可能是负数,还可能是0,故此选项错误,符合题意;
B、当时,分母,所以当时,分式无意义,故此选项正确,不符合题意;
C、当时,分母,分子,当时,分式的值为0,故此选项正确,不符合题意;
D、当时,分母,,当时,分式的值为1,故此选项正确,不符合题意.
故选:A.
8.B
【分析】本题考查分式的化简求值,利用分式化简法则将化简,再把代入即可,熟练掌握分式混合运算的法则是解题的关键.
【详解】解:,
,
,
,
,
原式,
故选:B.
9.D
【分析】本题主要考查、多项式除以单项式、多项式乘以多项式、分式的加减运算法则及平方差公式.分别根据多项式除以单项式、多项式乘以多项式、分式的加减运算法则及平方差公式逐一计算可得.
【详解】A、,此选项计算错误;
B、,此选项计算错误;
C、,此选项计算错误;
D、,此选项计算正确;
故选:D.
10.A
【分析】本题考查了分式的混合运算,理解并应用题目中的计算方法是解题的关键.
根据题目中的计算方法进行求解即可.
【详解】解:∵,
∴在原式中分母分子同除以,
即;
在面积是的矩形中设矩形的一边长为,则另一边长是,
矩形的周长是;
当矩形成为正方形时,就有(),
解得:,
这时矩形的周长最小,
因此()的最小值是.
故选:A.
11.
【分析】本题主要考查了分式的除法计算,根据分式的除法计算法则求出的结果即可得到答案.
【详解】解:∵,
∴
,
故答案为:.
12.且
【分析】本题主要考查了根据分式方程解的情况求参数,先解分式方程得到,再根据分式方程的解为正数以及方程不能有增根得到,解之即可得到答案.
【详解】解:
去分母得:,
去括号得:,
移项得:,
合并同类项得:,
系数化为1得:,
∵分式方程的解是正数,
∴,
∴且,
故答案为:且.
13.
【分析】本题考查分式的值为0的条件.分式的值是0的条件是,分子为0,分母不为0,进行求解即可.
【详解】解:由题意得,,
,,
,
即当时,分式的值是
故答案为:
14.2或/或2
【分析】本题考查了分式方程无解问题,分两种情况分别计算:当时,该整式方程无解,当时,由分式方程无解得到增根或,代入整式方程计算即可;熟练掌握分式方程无解的条件是:去分母后所得整式方程无解或解这个整式方程得到的解使原方程的分母等于零.
【详解】解:,
去分母得:,
整理得:,
当时,该整式方程无解,此时,
当时,要是原方程无解,则,即或,
把代入整式方程,的值不存在,
把代入整式方程,得,
综上所述,当或时,关于的分式方程无解,
故答案为:2或.
15.5、4、2、1
【分析】本题考查了分式方程的解,解一元一次不等式组.考虑到分式方程有可能产生增根的情形是解题的关键.利用解分式方程的一般步骤求得分式方程的解,由题意得到不等式;分式方程有可能产生使分母为0的增根,所以原方程的解不等于1,由以上两个条件即可得出答案.
【详解】解:去分母,得:
,
移项,合并同类项,得:
.
∵解为非负数,
∴,
∴.
∵原分式方程有可能产生增根,
∴,
∴,
∴正整数的值为5、4、2、1.
故答案为:5、4、2、1.
16.
【分析】本题考查分式方程的实际应用.根据乙班平均每人读书的本数是甲班平均每人读书的本数,列出分式方程即可.
【详解】解:设乙班有人,则甲班有人,由题意,得:;
故答案为:.
17.
【分析】本题考查了一元一次方程的应用、负指数幂计算及代数式求值,由题意可得到关于的两个方程,解方程即可求出的值,再把的值代入计算即可求解,根据题意,正确列出一元一次方程是解题的关键.
【详解】解:设右上角数字为x,右下角数字为y,
由题意可得,,,
解得,,
∴,
故选:.
18.8
【分析】本题考查分式的方程的应用,熟练解分式方程是正确解决本题的关键.
利用已知条件建立分式方程,并全面地进行分类讨论即可得出.
【详解】解:当时,,
,
不是整数,与题设矛盾,
,
令,
由题设m、n为正整数,
设,
由①得,
代入②,整理得,
是正整数,
或2或3,
又,
或,
当时,
由①②解得,(不合题意,舍去),
当时,
由①②解得,,
.
故答案为:8.
19.(1)
(2)1
(3)1
(4)
【分析】本题考查了整式的混合运算,绝对值,零指数幂,负整数指数幂,完全平方公式,平方差公式,准确熟练地进行计算是解题的关键.
(1)按照从左到右的顺序进行计算,即可解答;
(2)先化简各式,然后再进行计算即可解答;
(3)利用平方差公式进行计算,即可解答;
(4)利用完全平方公式,平方差公式进行计算,即可解答.
【详解】(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
.
20.(1);(2);时,原式
【分析】本题主要考查了分式化简求值,解题的关键是熟练掌握分式混合运算法则,准确计算.
(1)根据分式加减运算法则进行计算即可;
(2)先根据分式混合运算法则进行化简,然后再代入求值即可.
【详解】解:(1)
;
(2)
,
∵,,
∴,2,
把代入得:原式.
21.(1)甲每小时加工的零件数为个,乙组每小时加工的零件数为个
(2)m的值为10
【分析】本题考查了分式方程的应用,一元一次方程的应用,根据题意列出方程是解题的关键.
(1)设甲每小时加工的零件数为个,则乙组每小时加工的零件数为个,根据题意列出分式方程,解方程即可求解;
(2)分别表示出甲、乙每小时的加工的零件数量,根据题意,列出一元一次方程即可求解.
【详解】(1)解:设甲每小时加工的零件数为个,则乙组每小时加工的零件数为个,根据题意得:
,
解得:,
经检验,是原方程的解,
∴(个);
答:甲每小时加工的零件数为个,乙组每小时加工的零件数为个;
(2)解:依题意得:,
解得:,
答:m的值为10.
22.,
【分析】本题考查分式的化简求值,解题关键是掌握分式的混合运算法则.先根据分式的混合运算将式子化简,再将计算出的x的值代入计算即可.
【详解】解:原式
,
,
,
当时,原式.
23.(1)原方程无解;(2),当时,原式
【分析】本题主要考查了解分式方程,分式的化简求值:
(1)按照去分母,移项,合并同类项的步骤解方程,然后检验即可得到答案;
(2)先根据分式的混合计算法则化简,然后代值计算即可得到答案.
【详解】解:(1)
去分母得:,
移项得:,
合并同类项得:,
检验,当时,,
∴是原方程的增根,
∴原方程无解;
(2)
,
当时,原式=.
24.这家超市销售这种饮料每箱18瓶
【分析】本题考查了分式方程的应用,设品牌饮料每箱瓶,根据“买一箱送两瓶,这相当于每瓶按原价九折销售”列方程求解即可,根据题意找出等量关系是解题的关键.
【详解】解:设品牌饮料每箱瓶,则依据题意得:
解得:
经检验:是原方程的解
答:这家超市销售这种饮料每箱18瓶.
25.(1)是,理由见详解
(2),理由见详解;证明见详解
(3)
【分析】本题考查了整式的加减、分式的运算和分式方程,读懂题意是解题关键.
(1)根据“臻美数对”的定义即可求解;
(2)结合“臻美数对”的定义及整式的加减即可求解;
(3)由(2)的结合分式的加减即可求解.
【详解】(1)解:将与各自的十位数字和个位数字交换位置可得:,
,
与是“臻美数对;
(2),理由如下:
由题意得:
,
移项合并同类项可得:
,
左右两边同时除以9可得:
;
两“臻美数对”的和为:
两“臻美数对”的和是的倍数;
(3)这两个数为“臻美数对”,
即
解得:,
,;
,,
这两个数分别为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
