2024学年初中数学冀教版八年级下册 课件 21.4 一次函数的应用 第2课时(20张PPT)
文档属性
| 名称 | 2024学年初中数学冀教版八年级下册 课件 21.4 一次函数的应用 第2课时(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 373.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 19:38:14 | ||
图片预览








文档简介
(共20张PPT)
第二十一章 一次函数
21.4 一次函数的应用
第2课时
1.掌握两个一次函数图象的应用.
2.能利用函数图象解决数学问题.
合作探究
当堂检测
学习目标
课堂总结
20
0
40
60
80
100
单位:cm
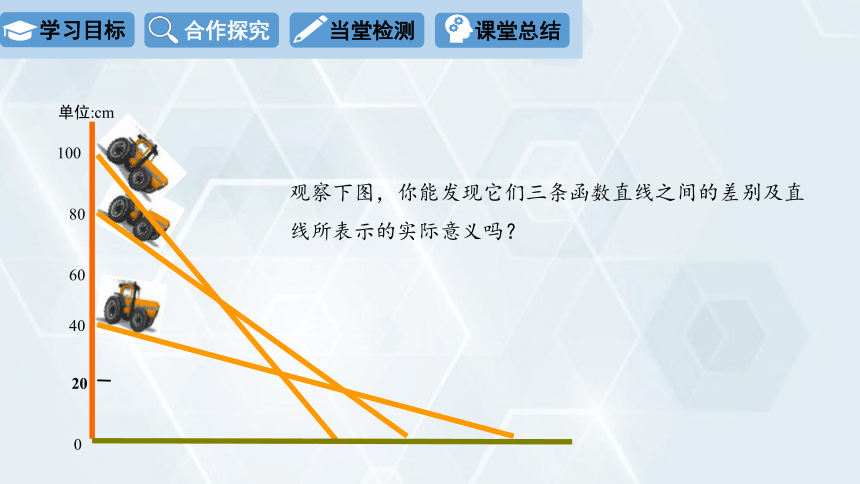
观察下图,你能发现它们三条函数直线之间的差别及直线所表示的实际意义吗?
合作探究
当堂检测
学习目标
课堂总结
活动1:“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
(1)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,y1,y2与x的函数关系图象如图所示,请结合图中信息分别求出y1,y2关于x的函数表达式;
探究
解析:(1)根据两家出租公司的收费标准,列出函数关系式即可.
合作探究
当堂检测
学习目标
课堂总结
解:(1)设y1=k1x+80,把点(1,95)代入,
可得k1+80=95,解得k1=15
∴y1=15x+80(x≥0)
设y2=k2x,把(1,30)代入,可得k2=30,
∴y2=30x(x≥0)
合作探究
当堂检测
学习目标
课堂总结
(2)请你帮助小明分析选择哪家出租公司合算.
解:由图可知:两个图象有交点,即:15x+80=30x
解得:x=
故当0<x< 时,乙出租公司合算;
当x= 时,甲、乙出租公司一样合算;
当x> 时,甲出租公司合算;
合作探究
当堂检测
学习目标
课堂总结
活动2:在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间的关系如图所示,请根据图象提供的信息解答下列问题:
甲
乙
合作探究
当堂检测
学习目标
课堂总结
(1)分别求出甲、乙两根蜡烛燃烧速度,及它们的y与x的函数关系式;
甲
乙
温馨提示:实际问题函数关系式一定要写取值范围,否则不符合实际.
合作探究
当堂检测
学习目标
课堂总结
解:(1)设甲的函数关系式为y=kx+b,乙:y=mx+n,
故甲的函数关系式:y=-4x+8 (0<x≤2)
乙的函数关系式:y=-2x+6(0<x≤3)
据图可知:甲 ,
乙 ,
解得: , ,
(2)燃烧多长时间,甲、乙两根蜡烛的高度相同(不考虑都燃尽的时间)?
解:(2)高度相同即y相等
可列出式子:-4x+8=-2x+6
解得:x=1
故燃烧1小时后,甲、乙两根蜡烛的高度相同
甲
乙
合作探究
当堂检测
学习目标
课堂总结
(3)在哪个时间段内,甲蜡烛比乙蜡烛高?在哪个时间段内,甲蜡烛比乙蜡烛矮?
解:(3)由(2)可知:图中交点的横坐标为1
由图可知:在燃烧0-1h时,甲蜡烛比乙高
在燃烧1h时,两根蜡烛一样高
在燃烧1-3h时,甲蜡烛比乙矮
甲
乙
合作探究
当堂检测
学习目标
课堂总结
总结
1.从数学角度分析实际问题,建立函数模型.
2.根据图像或者方程,求出自变量在不同取值时,对应的函数值大小关系.
合作探究
当堂检测
学习目标
课堂总结
练一练
1.如图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差 km/h,在行驶了 小时甲追上乙.
0.8
分析:根据图象可得出:甲的速度为
120÷5=24(km/h),
乙的速度为(120﹣4)÷5=23.2(km/h),
速度差为24﹣23.2=0.8(km/h)
5
合作探究
当堂检测
学习目标
课堂总结
D
1.小亮和小明周六到距学校24km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程S(km)与时间t(时)的函数图象如图所示.根据图象得到结论,其中错误的是( )
A.小亮骑自行车的平均速度是12km/h
B.小明比小亮提前0.5小时到达滨湖湿地公园
C.小明在距学校12km处追上小亮
D.9:30小明与小亮相距4km
合作探究
当堂检测
学习目标
课堂总结
2.我市某学校有两名教师带一名学生准备参加旅行团外出旅游,A旅行社告知:两名教师买全票,学生按半价优惠;B旅行社告知:三人旅游可按团体票计价,即每人按全价的 收费.若这两家旅行社每人的原票价相同,那么较优惠的旅行社是 (填“A”或“B”)旅行社.
B
分析:设原票价为x元,A旅行社的总费用为y1元,B旅行社的总费用为y2元.
根据题意,可得y1=2x+0.5x=2.5x,y2=3x· =2.4x,
∵x>0,∴y1>y2,
因此,较优惠的旅行社是B旅行社.
合作探究
当堂检测
学习目标
课堂总结
3.如图,l1反映了某公司的销售收入与销量的关系,l2 反映了该公司产品的销售成本与销量的关系,当该公司盈利(收入大于成本)时,销售量必须( )
A.小于12件 B.等于12件
C.大于12件 D.不低于12件
C
合作探究
当堂检测
学习目标
课堂总结
4.图书馆与学校相距600m,明明从学校出发步行去图书馆,亮亮从图书馆骑车去学校,两人同时出发,匀速相向而行,他们与学校的距离S(m)与时间t(s)的图象如图所示:
(1)明明的步行速度是 m/s;亮亮骑车的速度是 m/s.
(2)明明与学校的距离S与时间t的关系: ,
亮亮与学校的距离S与时间t的关系: .
(3)图中a的值为 .
2
3
合作探究
当堂检测
学习目标
课堂总结
S=2t
S=-3t+600
120
5.某剧院举行专场音乐会,成人票每张20元,学生票每张5元.暑假期间,为了丰富广大师生的业余文化生活,剧院制订了两种优惠方案供选择.
方案1:购买一张成人票送一张学生票;方案2:按总价的90%付款.
某校有4名老师与若干名(不少于4人)学生听音乐会.
(1)设学生人数为x,付款总金额为y元,分别求出两种优惠方案中y与x的函数解析式;
(2)求最节省费用的购票方案.
分析:方案1和方案2分别代表不同的函数,将实际问题转化为函数关系式,比较选择最优方案.
合作探究
当堂检测
学习目标
课堂总结
(1)设学生人数为x,付款总金额为y元,分别求出两种优惠方案中y与x的函数解析式;
解析:根据题意可列出按不同方案购票时关于x与y的函数关系式.
解:按优惠方案1购票,y1=20×4+(x-4)×5=5x+60(x≥4)
按优惠方案2购票,y2=(5x+20×4)×90%=4.5x+72(x≥4)
合作探究
当堂检测
学习目标
课堂总结
(2)求最节省费用的购票方案.
解:(2)当两种购票方案中购票费用相等时,有5x+60=4.5x+72
解得:x=24
当x<24时,选择方案1购票更节省;
当x=24时,方案1和方案2购票一样节省;
当x>24时,选择方案2购票更节省.
合作探究
当堂检测
学习目标
课堂总结
两个一次函数的应用
方案选择问题
实际生活中的问题
合作探究
当堂检测
学习目标
课堂总结
第二十一章 一次函数
21.4 一次函数的应用
第2课时
1.掌握两个一次函数图象的应用.
2.能利用函数图象解决数学问题.
合作探究
当堂检测
学习目标
课堂总结
20
0
40
60
80
100
单位:cm
观察下图,你能发现它们三条函数直线之间的差别及直线所表示的实际意义吗?
合作探究
当堂检测
学习目标
课堂总结
活动1:“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
(1)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,y1,y2与x的函数关系图象如图所示,请结合图中信息分别求出y1,y2关于x的函数表达式;
探究
解析:(1)根据两家出租公司的收费标准,列出函数关系式即可.
合作探究
当堂检测
学习目标
课堂总结
解:(1)设y1=k1x+80,把点(1,95)代入,
可得k1+80=95,解得k1=15
∴y1=15x+80(x≥0)
设y2=k2x,把(1,30)代入,可得k2=30,
∴y2=30x(x≥0)
合作探究
当堂检测
学习目标
课堂总结
(2)请你帮助小明分析选择哪家出租公司合算.
解:由图可知:两个图象有交点,即:15x+80=30x
解得:x=
故当0<x< 时,乙出租公司合算;
当x= 时,甲、乙出租公司一样合算;
当x> 时,甲出租公司合算;
合作探究
当堂检测
学习目标
课堂总结
活动2:在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间的关系如图所示,请根据图象提供的信息解答下列问题:
甲
乙
合作探究
当堂检测
学习目标
课堂总结
(1)分别求出甲、乙两根蜡烛燃烧速度,及它们的y与x的函数关系式;
甲
乙
温馨提示:实际问题函数关系式一定要写取值范围,否则不符合实际.
合作探究
当堂检测
学习目标
课堂总结
解:(1)设甲的函数关系式为y=kx+b,乙:y=mx+n,
故甲的函数关系式:y=-4x+8 (0<x≤2)
乙的函数关系式:y=-2x+6(0<x≤3)
据图可知:甲 ,
乙 ,
解得: , ,
(2)燃烧多长时间,甲、乙两根蜡烛的高度相同(不考虑都燃尽的时间)?
解:(2)高度相同即y相等
可列出式子:-4x+8=-2x+6
解得:x=1
故燃烧1小时后,甲、乙两根蜡烛的高度相同
甲
乙
合作探究
当堂检测
学习目标
课堂总结
(3)在哪个时间段内,甲蜡烛比乙蜡烛高?在哪个时间段内,甲蜡烛比乙蜡烛矮?
解:(3)由(2)可知:图中交点的横坐标为1
由图可知:在燃烧0-1h时,甲蜡烛比乙高
在燃烧1h时,两根蜡烛一样高
在燃烧1-3h时,甲蜡烛比乙矮
甲
乙
合作探究
当堂检测
学习目标
课堂总结
总结
1.从数学角度分析实际问题,建立函数模型.
2.根据图像或者方程,求出自变量在不同取值时,对应的函数值大小关系.
合作探究
当堂检测
学习目标
课堂总结
练一练
1.如图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差 km/h,在行驶了 小时甲追上乙.
0.8
分析:根据图象可得出:甲的速度为
120÷5=24(km/h),
乙的速度为(120﹣4)÷5=23.2(km/h),
速度差为24﹣23.2=0.8(km/h)
5
合作探究
当堂检测
学习目标
课堂总结
D
1.小亮和小明周六到距学校24km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程S(km)与时间t(时)的函数图象如图所示.根据图象得到结论,其中错误的是( )
A.小亮骑自行车的平均速度是12km/h
B.小明比小亮提前0.5小时到达滨湖湿地公园
C.小明在距学校12km处追上小亮
D.9:30小明与小亮相距4km
合作探究
当堂检测
学习目标
课堂总结
2.我市某学校有两名教师带一名学生准备参加旅行团外出旅游,A旅行社告知:两名教师买全票,学生按半价优惠;B旅行社告知:三人旅游可按团体票计价,即每人按全价的 收费.若这两家旅行社每人的原票价相同,那么较优惠的旅行社是 (填“A”或“B”)旅行社.
B
分析:设原票价为x元,A旅行社的总费用为y1元,B旅行社的总费用为y2元.
根据题意,可得y1=2x+0.5x=2.5x,y2=3x· =2.4x,
∵x>0,∴y1>y2,
因此,较优惠的旅行社是B旅行社.
合作探究
当堂检测
学习目标
课堂总结
3.如图,l1反映了某公司的销售收入与销量的关系,l2 反映了该公司产品的销售成本与销量的关系,当该公司盈利(收入大于成本)时,销售量必须( )
A.小于12件 B.等于12件
C.大于12件 D.不低于12件
C
合作探究
当堂检测
学习目标
课堂总结
4.图书馆与学校相距600m,明明从学校出发步行去图书馆,亮亮从图书馆骑车去学校,两人同时出发,匀速相向而行,他们与学校的距离S(m)与时间t(s)的图象如图所示:
(1)明明的步行速度是 m/s;亮亮骑车的速度是 m/s.
(2)明明与学校的距离S与时间t的关系: ,
亮亮与学校的距离S与时间t的关系: .
(3)图中a的值为 .
2
3
合作探究
当堂检测
学习目标
课堂总结
S=2t
S=-3t+600
120
5.某剧院举行专场音乐会,成人票每张20元,学生票每张5元.暑假期间,为了丰富广大师生的业余文化生活,剧院制订了两种优惠方案供选择.
方案1:购买一张成人票送一张学生票;方案2:按总价的90%付款.
某校有4名老师与若干名(不少于4人)学生听音乐会.
(1)设学生人数为x,付款总金额为y元,分别求出两种优惠方案中y与x的函数解析式;
(2)求最节省费用的购票方案.
分析:方案1和方案2分别代表不同的函数,将实际问题转化为函数关系式,比较选择最优方案.
合作探究
当堂检测
学习目标
课堂总结
(1)设学生人数为x,付款总金额为y元,分别求出两种优惠方案中y与x的函数解析式;
解析:根据题意可列出按不同方案购票时关于x与y的函数关系式.
解:按优惠方案1购票,y1=20×4+(x-4)×5=5x+60(x≥4)
按优惠方案2购票,y2=(5x+20×4)×90%=4.5x+72(x≥4)
合作探究
当堂检测
学习目标
课堂总结
(2)求最节省费用的购票方案.
解:(2)当两种购票方案中购票费用相等时,有5x+60=4.5x+72
解得:x=24
当x<24时,选择方案1购票更节省;
当x=24时,方案1和方案2购票一样节省;
当x>24时,选择方案2购票更节省.
合作探究
当堂检测
学习目标
课堂总结
两个一次函数的应用
方案选择问题
实际生活中的问题
合作探究
当堂检测
学习目标
课堂总结
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
