2024学年初中数学冀教版八年级下册 课件 22.5 菱形 第1课时(20张PPT)
文档属性
| 名称 | 2024学年初中数学冀教版八年级下册 课件 22.5 菱形 第1课时(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 583.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 19:41:20 | ||
图片预览






文档简介
(共20张PPT)
第1课时
第二十二章 四边形
22.5 菱形
1.理解菱形的定义,知道菱形是特殊的平行四边形
2.掌握菱形的性质定理
3.能应用菱形的性质定理解决相关计算或证明问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
观察图片中框出的图形,是你熟悉的图形吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
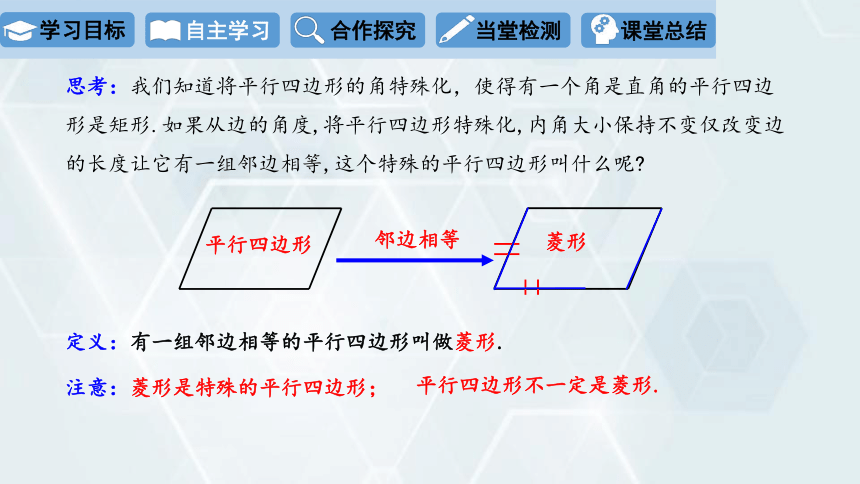
思考:我们知道将平行四边形的角特殊化,使得有一个角是直角的平行四边形是矩形.如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
菱形
邻边相等
定义:有一组邻边相等的平行四边形叫做菱形.
注意:菱形是特殊的平行四边形;
平行四边形不一定是菱形.
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:因为菱形是平行四边形,所以它具有平行四边形的所有性质,由于它有一组邻边相等,它是否具有一般平行四边形不具有的一些特殊性质呢?
活动1:请同学们拿出准备好的矩形纸片和小剪刀,利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片.
合作探究
当堂检测
学习目标
课堂总结
自主学习
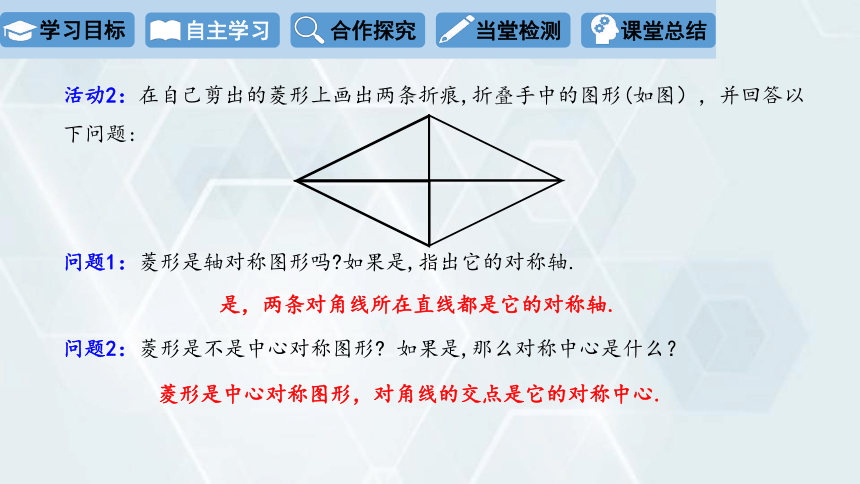
活动2:在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图),并回答以下问题:
问题1:菱形是轴对称图形吗 如果是,指出它的对称轴.
是,两条对角线所在直线都是它的对称轴.
问题2:菱形是不是中心对称图形 如果是,那么对称中心是什么?
菱形是中心对称图形,对角线的交点是它的对称中心.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图),并回答以下问题:
问题3:根据上面折叠过程,猜想菱形的四边在数量上有什么关系 菱形的两条对角线有什么关系
猜想1:菱形的四条边都相等;
猜想2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
合作探究
当堂检测
学习目标
课堂总结
自主学习
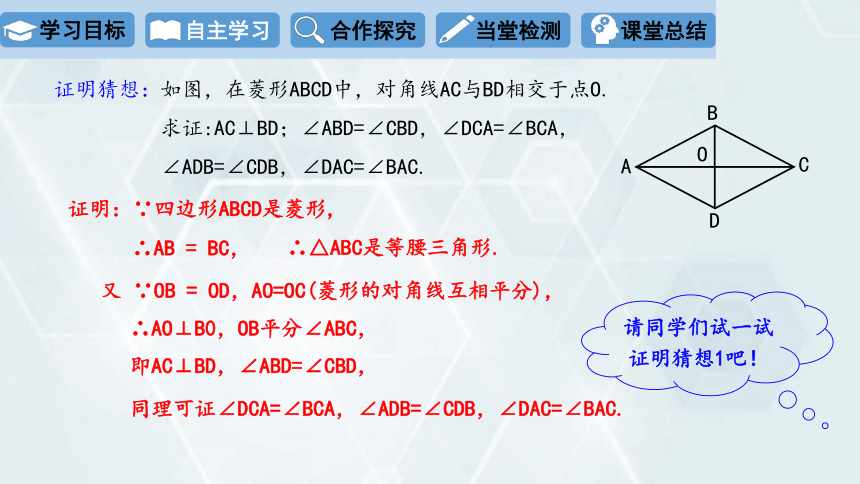
证明猜想:
如图,在菱形ABCD中,对角线AC与BD相交于点O.
求证:AC⊥BD;∠ABD=∠CBD,∠DCA=∠BCA,
∠ADB=∠CDB,∠DAC=∠BAC.
A
B
C
O
D
证明:∵四边形ABCD是菱形,
∴△ABC是等腰三角形.
∴AB = BC,
又 ∵OB = OD,AO=OC(菱形的对角线互相平分),
∴AO⊥B0,OB平分∠ABC,
即AC⊥BD,∠ABD=∠CBD,
同理可证∠DCA=∠BCA,∠ADB=∠CDB,∠DAC=∠BAC.
请同学们试一试证明猜想1吧!
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结
菱形除了具有平行四边形所有性质,还具有的性质:
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题4:菱形的对角线将菱形分成了四个小三角形,它们的面积相等吗 说一说你的理由.
相等,
问题5:前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢
理由:因为菱形的对角线互相垂直平分,
可利用SAS或SSS证明四个直角三角形全等.
即 S菱形ABCD=4S△AOB
A
B
C
D
O
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
O
你有什么发现?
菱形的面积 = 对角线乘积的一半
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一 菱形性质的运用
问题提出:在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
问题探究:
A
B
C
D
O
(1)题目让我们求菱形的边长和对角线的长,你能联想到
菱形的什么性质呢?
四条边都相等;
对角线互相垂直,且每条对角线平分一组对角.
(2)根据菱形的边和对角线的性质,结合题中已知∠BAC=30°,可以知道△ABD是 三角形,从而可得出边AB的长.
等边
(3)直角三角形中,已知斜边和一直角边的长,可根据 定理求出另一直角边的长,从而可求出对角线AC的长.
勾股
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一 菱形性质的运用
问题解决:
A
B
C
D
O
解:∵四边形ABCD是菱形,且∠BAC=30°,
∴△ABD是等边三角形,
∴AB=BD=6,即菱形的边长为6;
∴OB=OD= BD=3,
在Rt△AOB中,
∴AC=2OA= .
∴AB=AD,∠DAC=∠BAC=30°,
又 ∵AC⊥BD,
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
如图,在菱形ABCD中,AC=8,BD=6,则△ABD的周长等于( )
A.18 B.16 C.15 D.14
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 菱形的面积
问题提出:如图,四边形ABCD是边长为13cm的菱形,对角线长BD为10cm,求菱形ABCD的面积.
问题探究:
A
B
C
D
O
(1)你能联想到菱形面积的哪几种方法呢?
菱形对角线分成的四个三角形的面积和;
菱形对角线乘积的一半
(2)题中给出一对角线的长,只需要求 的长,就能求出菱形的面积.
另一对角线
(3)根据菱形边相等,对角线垂直平分的性质,结合勾股定理,即可求出另一条对角线的长,从而求出菱形的面积.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题解决:
探究二 菱形的面积
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD,OA=OC,
∴OB= BD=5,
在Rt△AOB中,
∴AC=2AO=24cm,
∴S菱形ABCD= AC·BD
= ×24×10
=120(cm2).
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.根据下图填一填:
(1)在菱形ABCD中,∠ABC=120 °,则∠BAC=_______.
(2)菱形ABCD的两条对角线长分别为6cm和8cm,则菱形的边长是_______.
A
B
C
O
D
30°
5cm
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=4cm.
(1)求BD的长;
(2)求菱形ABCD的面积.
解:(1)连接AC,交BD于点O,
∵AE⊥BC于点E,且BE=CE,
∴AB=AC,
∵在菱形ABCD中,AB=AD=4cm,AC⊥BD,AC=2AO,
∴根据勾股定理可知BO= cm,
∴BD= cm;
(2)菱形ABCD的面积为: AC BD
O
合作探究
当堂检测
学习目标
课堂总结
自主学习
∴AO=2cm,AO⊥BO,
3.如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:∠AFD=∠CBE.
证明:∵四边形ABCD是菱形,
∴CB=CD, CA平分∠BCD,
∴∠BCE=∠DCE,
又 CE=CE,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDE,
∵在菱形ABCD中,AB∥CD,
∴∠AFD=∠CDE,
A
D
C
B
F
E
∴∠AFD=∠CBE.
合作探究
当堂检测
学习目标
课堂总结
自主学习
菱形的相关概念及性质
具有平行四边行的一切性质
四条边都相等;
两条对角线互相垂直,并且每一条对角线平分一组对角.
有一组邻边相等的平行四边形叫做菱形
面积=对角线分成的四个三角形的面积和
=两条对角线乘积的一半
合作探究
当堂检测
学习目标
课堂总结
自主学习
第1课时
第二十二章 四边形
22.5 菱形
1.理解菱形的定义,知道菱形是特殊的平行四边形
2.掌握菱形的性质定理
3.能应用菱形的性质定理解决相关计算或证明问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
观察图片中框出的图形,是你熟悉的图形吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:我们知道将平行四边形的角特殊化,使得有一个角是直角的平行四边形是矩形.如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
菱形
邻边相等
定义:有一组邻边相等的平行四边形叫做菱形.
注意:菱形是特殊的平行四边形;
平行四边形不一定是菱形.
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:因为菱形是平行四边形,所以它具有平行四边形的所有性质,由于它有一组邻边相等,它是否具有一般平行四边形不具有的一些特殊性质呢?
活动1:请同学们拿出准备好的矩形纸片和小剪刀,利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图),并回答以下问题:
问题1:菱形是轴对称图形吗 如果是,指出它的对称轴.
是,两条对角线所在直线都是它的对称轴.
问题2:菱形是不是中心对称图形 如果是,那么对称中心是什么?
菱形是中心对称图形,对角线的交点是它的对称中心.
合作探究
当堂检测
学习目标
课堂总结
自主学习
活动2:在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图),并回答以下问题:
问题3:根据上面折叠过程,猜想菱形的四边在数量上有什么关系 菱形的两条对角线有什么关系
猜想1:菱形的四条边都相等;
猜想2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
合作探究
当堂检测
学习目标
课堂总结
自主学习
证明猜想:
如图,在菱形ABCD中,对角线AC与BD相交于点O.
求证:AC⊥BD;∠ABD=∠CBD,∠DCA=∠BCA,
∠ADB=∠CDB,∠DAC=∠BAC.
A
B
C
O
D
证明:∵四边形ABCD是菱形,
∴△ABC是等腰三角形.
∴AB = BC,
又 ∵OB = OD,AO=OC(菱形的对角线互相平分),
∴AO⊥B0,OB平分∠ABC,
即AC⊥BD,∠ABD=∠CBD,
同理可证∠DCA=∠BCA,∠ADB=∠CDB,∠DAC=∠BAC.
请同学们试一试证明猜想1吧!
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结
菱形除了具有平行四边形所有性质,还具有的性质:
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题4:菱形的对角线将菱形分成了四个小三角形,它们的面积相等吗 说一说你的理由.
相等,
问题5:前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢
理由:因为菱形的对角线互相垂直平分,
可利用SAS或SSS证明四个直角三角形全等.
即 S菱形ABCD=4S△AOB
A
B
C
D
O
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
O
你有什么发现?
菱形的面积 = 对角线乘积的一半
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一 菱形性质的运用
问题提出:在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
问题探究:
A
B
C
D
O
(1)题目让我们求菱形的边长和对角线的长,你能联想到
菱形的什么性质呢?
四条边都相等;
对角线互相垂直,且每条对角线平分一组对角.
(2)根据菱形的边和对角线的性质,结合题中已知∠BAC=30°,可以知道△ABD是 三角形,从而可得出边AB的长.
等边
(3)直角三角形中,已知斜边和一直角边的长,可根据 定理求出另一直角边的长,从而可求出对角线AC的长.
勾股
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一 菱形性质的运用
问题解决:
A
B
C
D
O
解:∵四边形ABCD是菱形,且∠BAC=30°,
∴△ABD是等边三角形,
∴AB=BD=6,即菱形的边长为6;
∴OB=OD= BD=3,
在Rt△AOB中,
∴AC=2OA= .
∴AB=AD,∠DAC=∠BAC=30°,
又 ∵AC⊥BD,
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
如图,在菱形ABCD中,AC=8,BD=6,则△ABD的周长等于( )
A.18 B.16 C.15 D.14
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 菱形的面积
问题提出:如图,四边形ABCD是边长为13cm的菱形,对角线长BD为10cm,求菱形ABCD的面积.
问题探究:
A
B
C
D
O
(1)你能联想到菱形面积的哪几种方法呢?
菱形对角线分成的四个三角形的面积和;
菱形对角线乘积的一半
(2)题中给出一对角线的长,只需要求 的长,就能求出菱形的面积.
另一对角线
(3)根据菱形边相等,对角线垂直平分的性质,结合勾股定理,即可求出另一条对角线的长,从而求出菱形的面积.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题解决:
探究二 菱形的面积
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD,OA=OC,
∴OB= BD=5,
在Rt△AOB中,
∴AC=2AO=24cm,
∴S菱形ABCD= AC·BD
= ×24×10
=120(cm2).
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.根据下图填一填:
(1)在菱形ABCD中,∠ABC=120 °,则∠BAC=_______.
(2)菱形ABCD的两条对角线长分别为6cm和8cm,则菱形的边长是_______.
A
B
C
O
D
30°
5cm
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=4cm.
(1)求BD的长;
(2)求菱形ABCD的面积.
解:(1)连接AC,交BD于点O,
∵AE⊥BC于点E,且BE=CE,
∴AB=AC,
∵在菱形ABCD中,AB=AD=4cm,AC⊥BD,AC=2AO,
∴根据勾股定理可知BO= cm,
∴BD= cm;
(2)菱形ABCD的面积为: AC BD
O
合作探究
当堂检测
学习目标
课堂总结
自主学习
∴AO=2cm,AO⊥BO,
3.如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:∠AFD=∠CBE.
证明:∵四边形ABCD是菱形,
∴CB=CD, CA平分∠BCD,
∴∠BCE=∠DCE,
又 CE=CE,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDE,
∵在菱形ABCD中,AB∥CD,
∴∠AFD=∠CDE,
A
D
C
B
F
E
∴∠AFD=∠CBE.
合作探究
当堂检测
学习目标
课堂总结
自主学习
菱形的相关概念及性质
具有平行四边行的一切性质
四条边都相等;
两条对角线互相垂直,并且每一条对角线平分一组对角.
有一组邻边相等的平行四边形叫做菱形
面积=对角线分成的四个三角形的面积和
=两条对角线乘积的一半
合作探究
当堂检测
学习目标
课堂总结
自主学习
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
