2024学年初中数学冀教版八年级下册 课件 第十九章 平面直角坐标系 复习课(共27张PPT)
文档属性
| 名称 | 2024学年初中数学冀教版八年级下册 课件 第十九章 平面直角坐标系 复习课(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 452.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 19:47:11 | ||
图片预览




文档简介
(共27张PPT)
第十九章 平面直角坐标系
复习课
1.能根据坐标描出点的位置,能由点的位置写出点的坐标.
2.掌握各象限及坐标轴上点的坐标特征,能建立适当的平面直角坐标系描述物体的位置,体会平面直角坐标系在解决实际问题中的作用.
3.知道平移与坐标的关系,能用坐标表示平移变换,进一步体会数形结合思想.
考点探究
当堂检测
学习目标
课堂总结
知识梳理
知识点1:有序数对
有序数对:有顺序的两个数a与b组成的数对叫做有序数对,记作(a,b).
有序数对
点的位置
思想方法:
(a,b)与(b,a)表示的是两个不同的位置.
注意点:
考点探究
当堂检测
学习目标
课堂总结
知识梳理
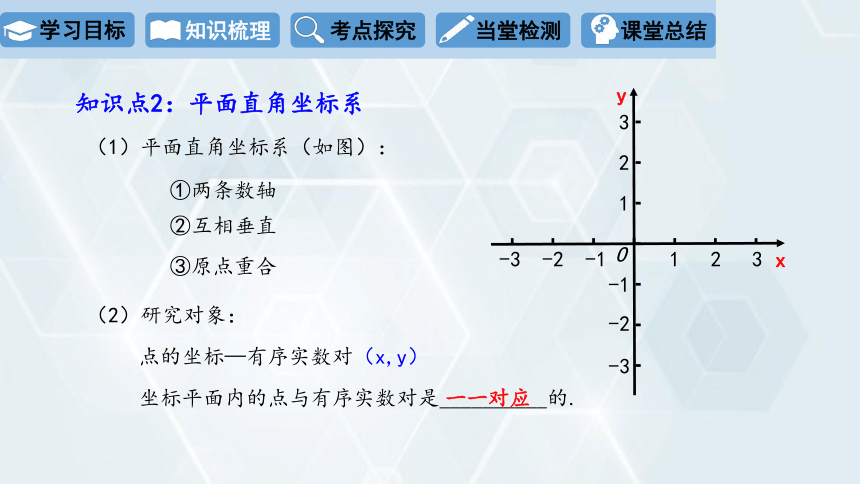
(1)平面直角坐标系(如图):
(2)研究对象:
点的坐标—有序实数对(x,y)
-3 -2 -1 1 2 3
x
O
-3
-2
-1
1
3
2
y
知识点2:平面直角坐标系
①两条数轴
②互相垂直
③原点重合
坐标平面内的点与有序实数对是__________的.
一一对应
考点探究
当堂检测
学习目标
课堂总结
知识梳理
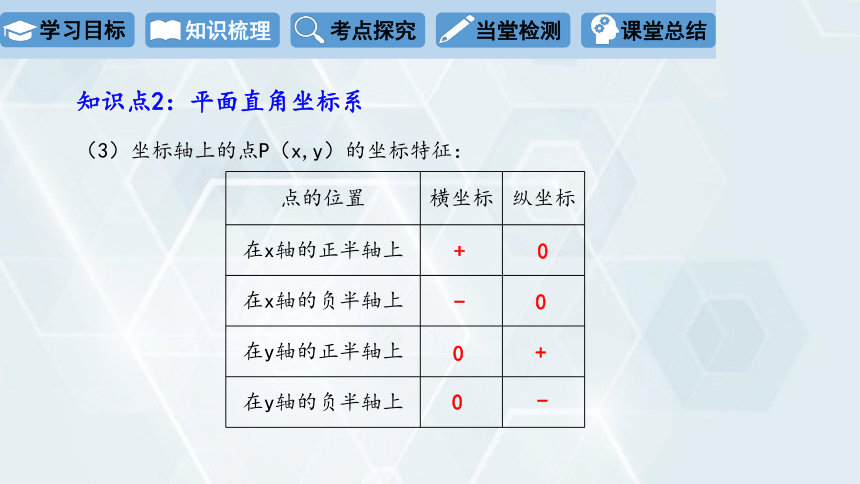
(3)坐标轴上的点P(x,y)的坐标特征:
知识点2:平面直角坐标系
点的位置 横坐标 纵坐标
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
考点探究
当堂检测
学习目标
课堂总结
知识梳理
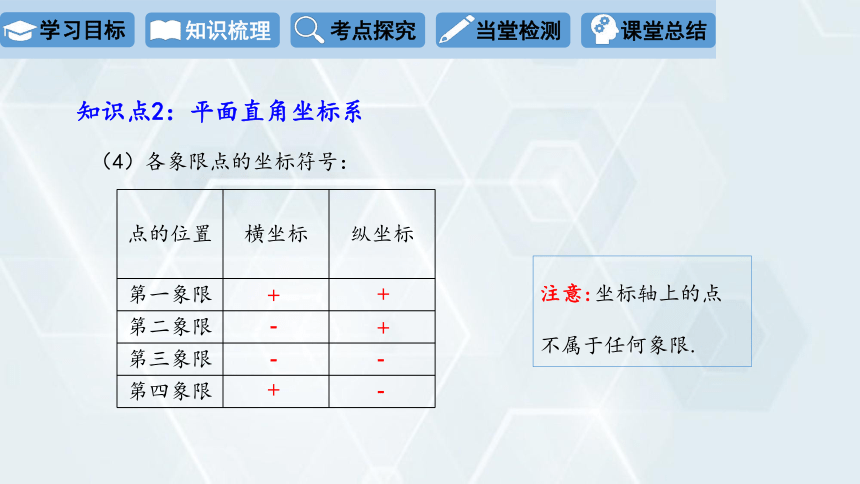
(4)各象限点的坐标符号:
注意:坐标轴上的点
不属于任何象限.
知识点2:平面直角坐标系
点的位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
考点探究
当堂检测
学习目标
课堂总结
知识梳理
(1)用坐标表示地理位置:
知识点3:坐标方法的简单应用
①利用平面直角坐标系表示地理位置
②用方向和距离表示具体位置
坐标原点
x轴
正方向
单位长度
名称
坐标
建立坐标系,选择一个适当的参照点为 ,确定 、_____ 的 ;
根据具体问题确定___________;
在坐标平面内画出这些点,写出各点的 和各个地点的 .
y轴
考点探究
当堂检测
学习目标
课堂总结
知识梳理
知识点3:坐标方法的简单应用
(2)用坐标表示平移:
平移方向和平移距离 对应点的坐标
向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
(x+a , y+b)
(x+a , y-b)
(x-a , y+b)
(x-a , y-b)
考点探究
当堂检测
学习目标
课堂总结
知识梳理
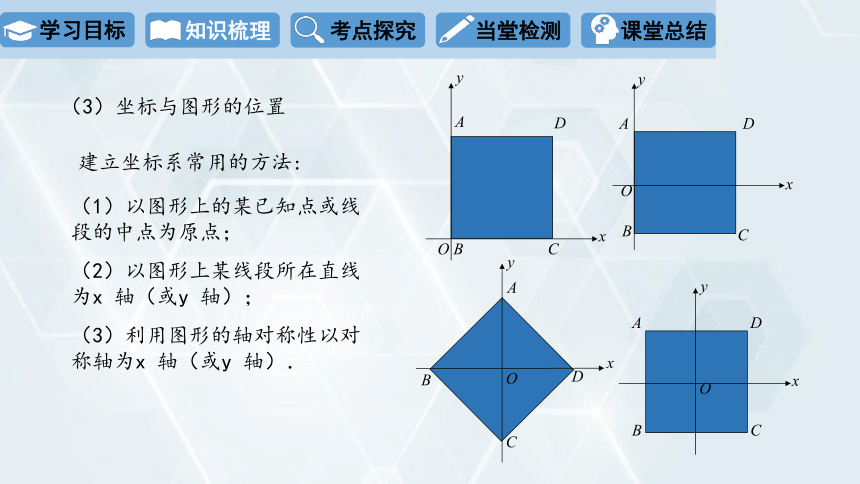
(3)坐标与图形的位置
考点探究
当堂检测
学习目标
课堂总结
知识梳理
A
D
C
B
y
x
O
A
B
C
D
y
x
O
A
B
C
D
y
x
O
A
B
C
D
x
y
O
建立坐标系常用的方法:
(1)以图形上的某已知点或线段的中点为原点;
(2)以图形上某线段所在直线为x 轴(或y 轴);
(3)利用图形的轴对称性以对称轴为x 轴(或y 轴).
(4)图形的轴对称与坐标变化
考点探究
当堂检测
学习目标
课堂总结
知识梳理
关于x轴成对称的两个图形,各对应顶点的横坐标相等,纵坐标互为相反数.
关于y轴成对称的两个图形,各对应顶点的横坐标互为相反数,纵坐标相等.
(5)图形的放缩与坐标变化规律
考点探究
当堂检测
学习目标
课堂总结
知识梳理
将一个图形各顶点的横坐标和纵坐标都乘以k(或 ,k>1),所得图形的形状 ,各边扩大为原来的 倍(或缩小为原来的 ),且连接各对应顶点的直线 .
不变
k
交于一点
考点一:有序数对
例1.某个英文词的字母顺序分别对应下图中的有序数对(6,2),(1,1),(6,3),(1,2),(5,3),则这个英文单词的是什么?
解:按照对应关系可知:
(5,3)→S,
(1,2)→H,
(6,3)→T,
(1,1)→A,
(6,2)→M,
故这个单词是MATHS.
考点探究
当堂检测
学习目标
课堂总结
知识梳理
1.下列关于有序数对的说法正确的是( )
A.(3,2)与(2,3)表示的位置相同
B.(a,b)与(b,a)表示的位置一定不同
C.(3,-2)与(-2,3)是表示不同位置的两个有序数对
D.(4,4)与(4,4)表示两个不同的位置
C
考点探究
当堂检测
学习目标
课堂总结
知识梳理
例2.点P位于y轴左方,距y轴3个单位长;位于x轴上方,距x轴4个单位长,
(1)求点P的坐标,并分析点P位于哪一个象限;
解:(1)∵ 点P 位于y轴左方,∴ 点的横坐标小于0;
考点二:平面直角坐标系
∴ 点P的坐标(-3,4);∴ 点P位于第二象限.
∵距x 轴4个单位长;∴ 点P 的纵坐标是4.
又∵ P 点位于x 轴上方,∴ 点的纵坐标大于0;
∵ 距y 轴3个单位长,∴ 点P 的横坐标是﹣3;
考点探究
当堂检测
学习目标
课堂总结
知识梳理
(2)若MP平行于x轴,线段MP=3,求点M的坐标,并分析位置.
解:由(1)可知:点P(-3,4)
综上所述:点M的坐标为(0,4),位于y轴正半轴上
或点M的坐标为(-6,4),位于第二象限.
点M在点P的正右方,则x-(-3)=3,可得x=0,此时M(0,4)
点M在点P的正左方,则-3-x=3,可得x=-6,此时M(-6,4)
又∵MP=3, ∴点M与点P的横坐标的差的绝对值为3,即|-3-x|=3
∵MP平行于x轴,∴点M的坐标为(x,4)
考点探究
当堂检测
学习目标
课堂总结
知识梳理
归纳总结:
1. 坐标轴上的点:
②平行于y轴:横坐标相同,纵坐标不同
①平行于x轴:横坐标不同,纵坐标相同
2. 平行于坐标轴的直线上的点:
① 在x轴上的点:(x,0)
② 在y轴上的点:(0,y)
考点探究
当堂检测
学习目标
课堂总结
知识梳理
2.在平面直角坐标系中,点A(2m-7,n-6)在第四象限,到x、y轴的距离分别是3和1,试求m+n的值.
解:∵ 点A位于第四象限; 根据第四象限点的特征(+,-);
∴ m+n=7.
∴ 2m-7=1,n-6=-3; ∴ m=4,n=3;
∴ 点A的纵坐标是-3,横坐标是1.
又∵ 点A距x轴3个单位长,距y轴1个单位长;
考点探究
当堂检测
学习目标
课堂总结
知识梳理
3.在平面直角坐标系中,已知点A(-2,4),AB=4,且AB∥x轴,求点B的坐标,并分析点B可能出现在那几个象限.
解:∵点A(-2,4),且 AB∥x轴
∴点B的坐标(2,4)或(-6,4);可能出现在第一、二象限.
点B在点A正左方,则-2-x=4,可得x=-6,故B(-6,4)
点B在点A正右方,则x-(-2)=4,可得x=2,故B(2,4)
AB的长度等于点A与点B横坐标差的绝对值,即|-2-x|=4
∴点B的坐标为(x,4)
考点探究
当堂检测
学习目标
课堂总结
知识梳理
例3.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
解:答案不唯一,如:
考点三:坐标表示地理位置
以南门的位置作为原点每个小正方形的边长为1个单位长度建立直角坐标系,
x
y
O
南门(0,0),
马(-3,-3),
两栖动物(4,1),
飞禽(3,4).
狮子(-4,5),
考点探究
当堂检测
学习目标
课堂总结
知识梳理
4.张老师在一次课外活动中组织学生做“寻宝”游戏,他事先将“宝”埋好,然后在附近插了两个标签,并指出A、B两个标签和“宝藏”的坐标分别为(6,5)、(6,-5)和(-1,-3)(单位:米).你能画出“草图”并在图上准确地标注“宝藏”的位置指导同学们寻宝吗
x
y
宝藏
考点探究
当堂检测
学习目标
课堂总结
知识梳理
考点四:坐标表示平移
1
o
x
(-3,2)
(-2,-1)
(3,0)
例4.如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将三角形ABC作同样的平移得到三角形A1B1C1.求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
C
A1
C1
B1
A
解:A(-3,2)经平移后得到(-3+2,2+4),即A1(-1,6);
C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
B(-2,-1)经平移后得到(-2+2,-1+4),即B1(0,3);
考点探究
当堂检测
学习目标
课堂总结
知识梳理
为了更加直观、便捷地表示一些图形,或具体事物的位置,通常采用坐标方法.观察一个图形进行了怎样的平移,关键是抓住对应点进行了怎样的平移.
归纳总结:
考点探究
当堂检测
学习目标
课堂总结
知识梳理
例5.将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系.
(1)纵坐标不变,横坐标分别乘以-1.
解:坐标变化如下表,
根据坐标描出对应点,并依次连线
结果如图.
所得图形与原图形关于y轴对称
2 3 4 5 6 7 8
3
2
4
5
变化前 (3.0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4)
变化后 (-3,0) (-7,0) (-2,2) (-3,2) (-7,2) (-8,2) (-5,4)
-8
-7
-3
-6
-5
-4
-2
-1
关于y轴对称的点的坐标:
纵坐标相同,横坐标互为相反数
考点探究
当堂检测
学习目标
课堂总结
知识梳理
例5.将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系.
(2)横坐标不变,纵坐标分别乘以-1.
2 3 4 5 6 7 8
3
2
4
5
坐标变化如下表,
根据坐标描出对应点,并依次连线
结果如图.
所得图形与原图形关于x轴对称
变化前 (3.0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4)
变化后 (3,0) (7,0) (2,-2) (3,-2) (7,-2) (8,-2) (5,-4)
-1
-2
-3
-4
关于x轴对称的点的坐标:
横坐标相同,纵坐标互为相反数
考点探究
当堂检测
学习目标
课堂总结
知识梳理
5.如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).请画出上述平移后的三角形A1B1C1,并写出点A、C、A1、C1的坐标.
1
y
O
1
x
A
B
C
A1
B1
C1
P
P1
解:A(-3,2)、
C(-2,0)、
A1(3,4)、
C1(4,2).
考点探究
当堂检测
学习目标
课堂总结
知识梳理
6.如图,在直角坐标系中,A(-1,5),B(-3,0),C(-4,3).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)写出点C1的坐标.
解:(1)如图所示
(2)点C1的坐标为:(4,3).
考点探究
当堂检测
学习目标
课堂总结
知识梳理
A1
B1
C1
考点探究
当堂检测
学习目标
课堂总结
知识梳理
确定平面上物体的位置
方位角和距离
坐标与图形的位置
点的坐标
平面直角坐标系
坐标与图形的变化
轴对称
平移
放缩
第十九章 平面直角坐标系
复习课
1.能根据坐标描出点的位置,能由点的位置写出点的坐标.
2.掌握各象限及坐标轴上点的坐标特征,能建立适当的平面直角坐标系描述物体的位置,体会平面直角坐标系在解决实际问题中的作用.
3.知道平移与坐标的关系,能用坐标表示平移变换,进一步体会数形结合思想.
考点探究
当堂检测
学习目标
课堂总结
知识梳理
知识点1:有序数对
有序数对:有顺序的两个数a与b组成的数对叫做有序数对,记作(a,b).
有序数对
点的位置
思想方法:
(a,b)与(b,a)表示的是两个不同的位置.
注意点:
考点探究
当堂检测
学习目标
课堂总结
知识梳理
(1)平面直角坐标系(如图):
(2)研究对象:
点的坐标—有序实数对(x,y)
-3 -2 -1 1 2 3
x
O
-3
-2
-1
1
3
2
y
知识点2:平面直角坐标系
①两条数轴
②互相垂直
③原点重合
坐标平面内的点与有序实数对是__________的.
一一对应
考点探究
当堂检测
学习目标
课堂总结
知识梳理
(3)坐标轴上的点P(x,y)的坐标特征:
知识点2:平面直角坐标系
点的位置 横坐标 纵坐标
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
考点探究
当堂检测
学习目标
课堂总结
知识梳理
(4)各象限点的坐标符号:
注意:坐标轴上的点
不属于任何象限.
知识点2:平面直角坐标系
点的位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
考点探究
当堂检测
学习目标
课堂总结
知识梳理
(1)用坐标表示地理位置:
知识点3:坐标方法的简单应用
①利用平面直角坐标系表示地理位置
②用方向和距离表示具体位置
坐标原点
x轴
正方向
单位长度
名称
坐标
建立坐标系,选择一个适当的参照点为 ,确定 、_____ 的 ;
根据具体问题确定___________;
在坐标平面内画出这些点,写出各点的 和各个地点的 .
y轴
考点探究
当堂检测
学习目标
课堂总结
知识梳理
知识点3:坐标方法的简单应用
(2)用坐标表示平移:
平移方向和平移距离 对应点的坐标
向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
(x+a , y+b)
(x+a , y-b)
(x-a , y+b)
(x-a , y-b)
考点探究
当堂检测
学习目标
课堂总结
知识梳理
(3)坐标与图形的位置
考点探究
当堂检测
学习目标
课堂总结
知识梳理
A
D
C
B
y
x
O
A
B
C
D
y
x
O
A
B
C
D
y
x
O
A
B
C
D
x
y
O
建立坐标系常用的方法:
(1)以图形上的某已知点或线段的中点为原点;
(2)以图形上某线段所在直线为x 轴(或y 轴);
(3)利用图形的轴对称性以对称轴为x 轴(或y 轴).
(4)图形的轴对称与坐标变化
考点探究
当堂检测
学习目标
课堂总结
知识梳理
关于x轴成对称的两个图形,各对应顶点的横坐标相等,纵坐标互为相反数.
关于y轴成对称的两个图形,各对应顶点的横坐标互为相反数,纵坐标相等.
(5)图形的放缩与坐标变化规律
考点探究
当堂检测
学习目标
课堂总结
知识梳理
将一个图形各顶点的横坐标和纵坐标都乘以k(或 ,k>1),所得图形的形状 ,各边扩大为原来的 倍(或缩小为原来的 ),且连接各对应顶点的直线 .
不变
k
交于一点
考点一:有序数对
例1.某个英文词的字母顺序分别对应下图中的有序数对(6,2),(1,1),(6,3),(1,2),(5,3),则这个英文单词的是什么?
解:按照对应关系可知:
(5,3)→S,
(1,2)→H,
(6,3)→T,
(1,1)→A,
(6,2)→M,
故这个单词是MATHS.
考点探究
当堂检测
学习目标
课堂总结
知识梳理
1.下列关于有序数对的说法正确的是( )
A.(3,2)与(2,3)表示的位置相同
B.(a,b)与(b,a)表示的位置一定不同
C.(3,-2)与(-2,3)是表示不同位置的两个有序数对
D.(4,4)与(4,4)表示两个不同的位置
C
考点探究
当堂检测
学习目标
课堂总结
知识梳理
例2.点P位于y轴左方,距y轴3个单位长;位于x轴上方,距x轴4个单位长,
(1)求点P的坐标,并分析点P位于哪一个象限;
解:(1)∵ 点P 位于y轴左方,∴ 点的横坐标小于0;
考点二:平面直角坐标系
∴ 点P的坐标(-3,4);∴ 点P位于第二象限.
∵距x 轴4个单位长;∴ 点P 的纵坐标是4.
又∵ P 点位于x 轴上方,∴ 点的纵坐标大于0;
∵ 距y 轴3个单位长,∴ 点P 的横坐标是﹣3;
考点探究
当堂检测
学习目标
课堂总结
知识梳理
(2)若MP平行于x轴,线段MP=3,求点M的坐标,并分析位置.
解:由(1)可知:点P(-3,4)
综上所述:点M的坐标为(0,4),位于y轴正半轴上
或点M的坐标为(-6,4),位于第二象限.
点M在点P的正右方,则x-(-3)=3,可得x=0,此时M(0,4)
点M在点P的正左方,则-3-x=3,可得x=-6,此时M(-6,4)
又∵MP=3, ∴点M与点P的横坐标的差的绝对值为3,即|-3-x|=3
∵MP平行于x轴,∴点M的坐标为(x,4)
考点探究
当堂检测
学习目标
课堂总结
知识梳理
归纳总结:
1. 坐标轴上的点:
②平行于y轴:横坐标相同,纵坐标不同
①平行于x轴:横坐标不同,纵坐标相同
2. 平行于坐标轴的直线上的点:
① 在x轴上的点:(x,0)
② 在y轴上的点:(0,y)
考点探究
当堂检测
学习目标
课堂总结
知识梳理
2.在平面直角坐标系中,点A(2m-7,n-6)在第四象限,到x、y轴的距离分别是3和1,试求m+n的值.
解:∵ 点A位于第四象限; 根据第四象限点的特征(+,-);
∴ m+n=7.
∴ 2m-7=1,n-6=-3; ∴ m=4,n=3;
∴ 点A的纵坐标是-3,横坐标是1.
又∵ 点A距x轴3个单位长,距y轴1个单位长;
考点探究
当堂检测
学习目标
课堂总结
知识梳理
3.在平面直角坐标系中,已知点A(-2,4),AB=4,且AB∥x轴,求点B的坐标,并分析点B可能出现在那几个象限.
解:∵点A(-2,4),且 AB∥x轴
∴点B的坐标(2,4)或(-6,4);可能出现在第一、二象限.
点B在点A正左方,则-2-x=4,可得x=-6,故B(-6,4)
点B在点A正右方,则x-(-2)=4,可得x=2,故B(2,4)
AB的长度等于点A与点B横坐标差的绝对值,即|-2-x|=4
∴点B的坐标为(x,4)
考点探究
当堂检测
学习目标
课堂总结
知识梳理
例3.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
解:答案不唯一,如:
考点三:坐标表示地理位置
以南门的位置作为原点每个小正方形的边长为1个单位长度建立直角坐标系,
x
y
O
南门(0,0),
马(-3,-3),
两栖动物(4,1),
飞禽(3,4).
狮子(-4,5),
考点探究
当堂检测
学习目标
课堂总结
知识梳理
4.张老师在一次课外活动中组织学生做“寻宝”游戏,他事先将“宝”埋好,然后在附近插了两个标签,并指出A、B两个标签和“宝藏”的坐标分别为(6,5)、(6,-5)和(-1,-3)(单位:米).你能画出“草图”并在图上准确地标注“宝藏”的位置指导同学们寻宝吗
x
y
宝藏
考点探究
当堂检测
学习目标
课堂总结
知识梳理
考点四:坐标表示平移
1
o
x
(-3,2)
(-2,-1)
(3,0)
例4.如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将三角形ABC作同样的平移得到三角形A1B1C1.求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
C
A1
C1
B1
A
解:A(-3,2)经平移后得到(-3+2,2+4),即A1(-1,6);
C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
B(-2,-1)经平移后得到(-2+2,-1+4),即B1(0,3);
考点探究
当堂检测
学习目标
课堂总结
知识梳理
为了更加直观、便捷地表示一些图形,或具体事物的位置,通常采用坐标方法.观察一个图形进行了怎样的平移,关键是抓住对应点进行了怎样的平移.
归纳总结:
考点探究
当堂检测
学习目标
课堂总结
知识梳理
例5.将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系.
(1)纵坐标不变,横坐标分别乘以-1.
解:坐标变化如下表,
根据坐标描出对应点,并依次连线
结果如图.
所得图形与原图形关于y轴对称
2 3 4 5 6 7 8
3
2
4
5
变化前 (3.0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4)
变化后 (-3,0) (-7,0) (-2,2) (-3,2) (-7,2) (-8,2) (-5,4)
-8
-7
-3
-6
-5
-4
-2
-1
关于y轴对称的点的坐标:
纵坐标相同,横坐标互为相反数
考点探究
当堂检测
学习目标
课堂总结
知识梳理
例5.将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系.
(2)横坐标不变,纵坐标分别乘以-1.
2 3 4 5 6 7 8
3
2
4
5
坐标变化如下表,
根据坐标描出对应点,并依次连线
结果如图.
所得图形与原图形关于x轴对称
变化前 (3.0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4)
变化后 (3,0) (7,0) (2,-2) (3,-2) (7,-2) (8,-2) (5,-4)
-1
-2
-3
-4
关于x轴对称的点的坐标:
横坐标相同,纵坐标互为相反数
考点探究
当堂检测
学习目标
课堂总结
知识梳理
5.如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).请画出上述平移后的三角形A1B1C1,并写出点A、C、A1、C1的坐标.
1
y
O
1
x
A
B
C
A1
B1
C1
P
P1
解:A(-3,2)、
C(-2,0)、
A1(3,4)、
C1(4,2).
考点探究
当堂检测
学习目标
课堂总结
知识梳理
6.如图,在直角坐标系中,A(-1,5),B(-3,0),C(-4,3).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)写出点C1的坐标.
解:(1)如图所示
(2)点C1的坐标为:(4,3).
考点探究
当堂检测
学习目标
课堂总结
知识梳理
A1
B1
C1
考点探究
当堂检测
学习目标
课堂总结
知识梳理
确定平面上物体的位置
方位角和距离
坐标与图形的位置
点的坐标
平面直角坐标系
坐标与图形的变化
轴对称
平移
放缩
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
