人教版八年级数学下册第十七章《勾股定理》单元复习与检测(含解析)
文档属性
| 名称 | 人教版八年级数学下册第十七章《勾股定理》单元复习与检测(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 21:33:18 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版八年级数学下册第十七章《勾股定理》单元复习与检测
选择题(本大题共有10个小题,每小题3分,共30分)
如图,一棵大树在一次强风中于离地面3m处折断倒下,树干顶部在离根部4m处,
这棵大树在折断前的高度为( )m.
A.3 B.4 C.5 D.8
2 . ABC中,∠A,∠B,∠C的对边分别记为a,b,c,
由下列条件不能判定ABC为直角三角形的是( )
A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:3
C.a2=c2﹣b2 D.a:b:c=3:4:6
3. 如图是一个直角三角形,它的未知边的长x等于( )
A.13 B. C.5 D.
4 . 张大爷离家出门散步,他先向正东走了30 m,接着又向正南走了40 m,
此时他离家的距离为( )
A.30 m B.40 m C.50 m D.70 m
已知a,b,c是三角形的三边长,如果满足(a-6)2++|c-10|=0,
那么下列说法中不正确的是( )
A.这个三角形是直角三角形 B.这个三角形的最长边长是10
C.这个三角形的面积是48 D.这个三角形的最长边上的高是4.8
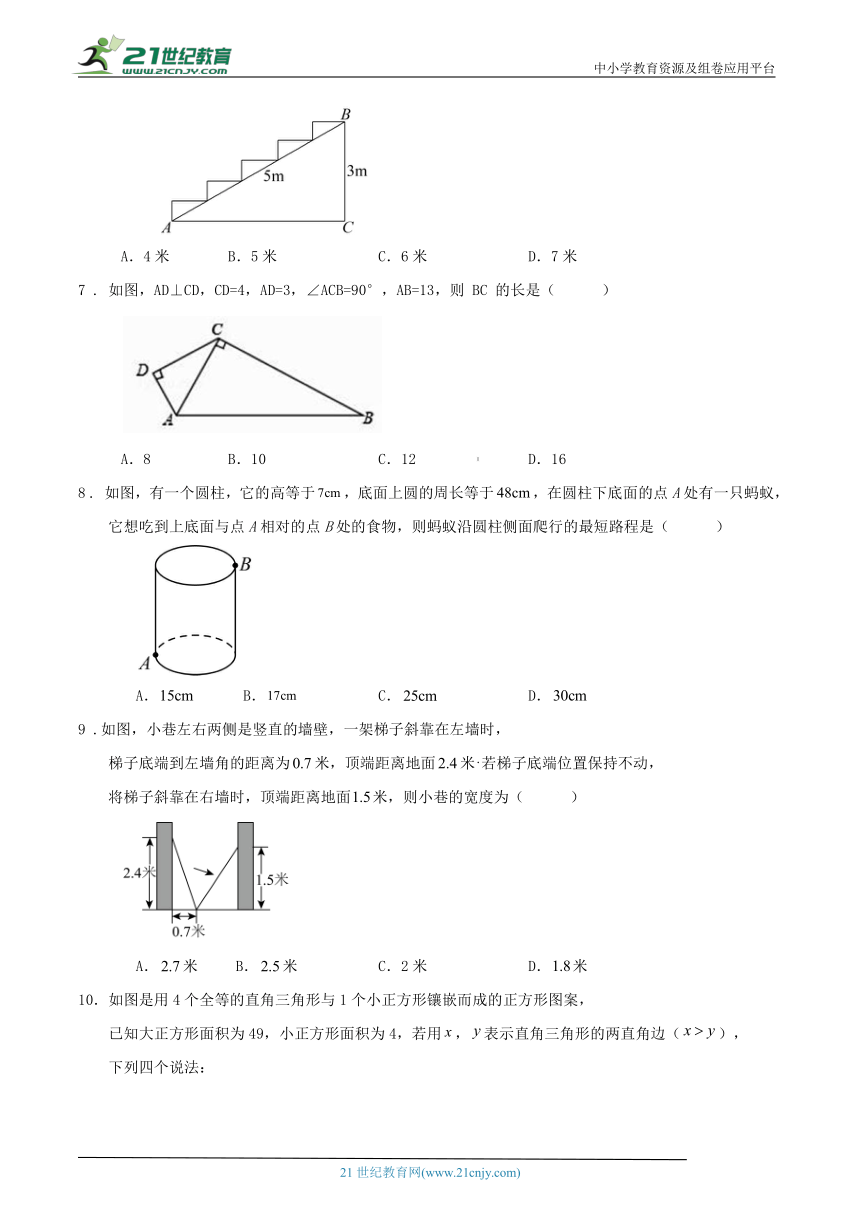
6. 如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A.4米 B.5米 C.6米 D.7米
7 . 如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则 BC 的长是( )
A.8 B.10 C.12 D.16
8 . 如图,有一个圆柱,它的高等于,底面上圆的周长等于,在圆柱下底面的点A处有一只蚂蚁,
它想吃到上底面与点A相对的点B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程是( )
A. B. C. D.
9 .如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,
梯子底端到左墙角的距离为米,顶端距离地面米若梯子底端位置保持不动,
将梯子斜靠在右墙时,顶端距离地面米,则小巷的宽度为( )
A.米 B.米 C.2米 D.米
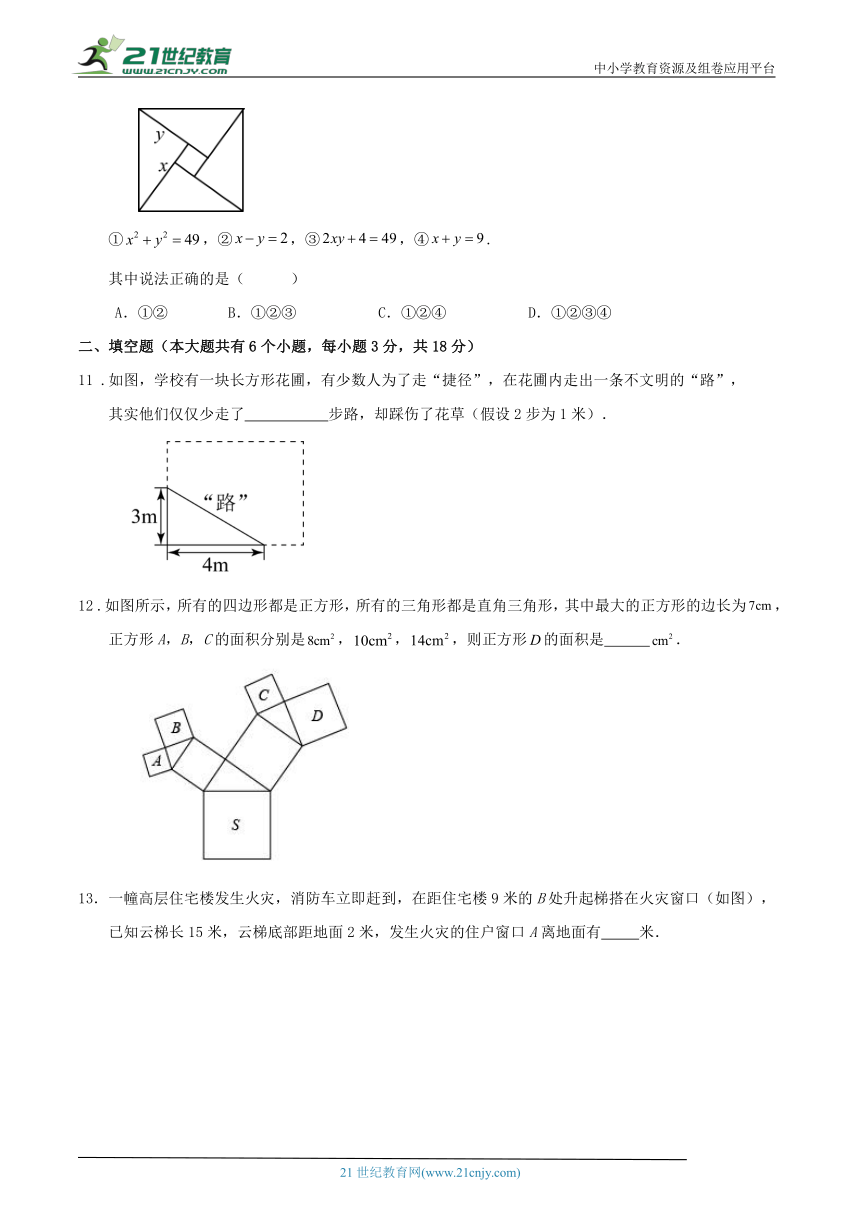
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,
已知大正方形面积为49,小正方形面积为4,若用,表示直角三角形的两直角边(),
下列四个说法:
①,②,③,④.
其中说法正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
填空题(本大题共有6个小题,每小题3分,共18分)
11 .如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,
其实他们仅仅少走了 步路,却踩伤了花草(假设2步为1米).
12 .如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为,
正方形A,B,C的面积分别是,,,则正方形的面积是 .
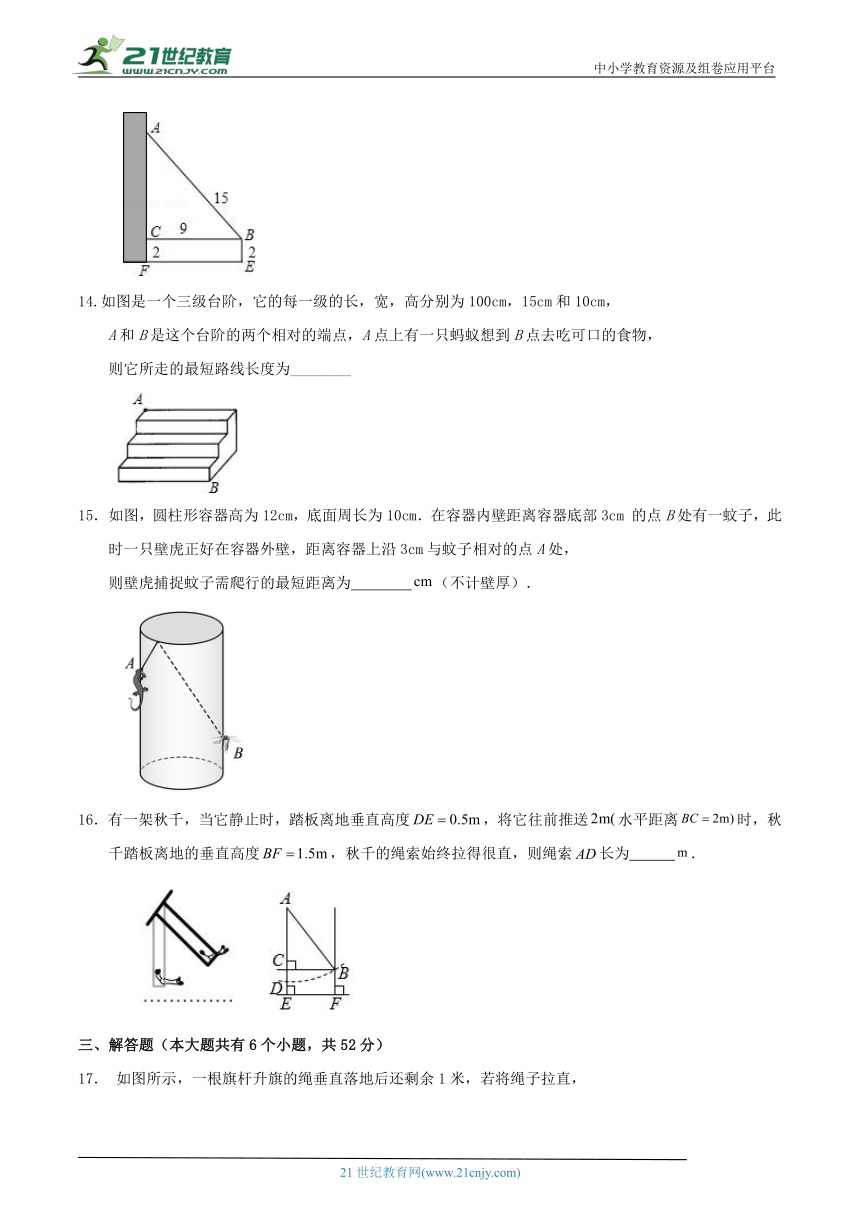
13.一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有 米.
14.如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,
A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,
则它所走的最短路线长度为________
如图,圆柱形容器高为12cm,底面周长为10cm.在容器内壁距离容器底部3cm 的点B处有一蚊子,此时一只壁虎正好在容器外壁,距离容器上沿3cm与蚊子相对的点A处,
则壁虎捕捉蚊子需爬行的最短距离为 (不计壁厚).
16.有一架秋千,当它静止时,踏板离地垂直高度,将它往前推送水平距离时,秋千踏板离地的垂直高度,秋千的绳索始终拉得很直,则绳索长为 .
三、解答题(本大题共有6个小题,共52分)
17. 如图所示,一根旗杆升旗的绳垂直落地后还剩余1米,若将绳子拉直,
则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.
如图,有一只小鸟在一棵高的大树树梢上捉虫子,
它的伙伴在离该树,高的一棵小树树梢.上发出友好的叫声,
它立刻以的速度飞向小树树梢,那么这只小鸟至少几秒才可能到达小树和伙伴在一起?
19 . 如图所示,四边形,,,,,,
求四边形的面积.
20 . 为了丰富少年儿童的业余生活,某社区要在如图中的所在的直线上建一图书室,
本社区有两所学校所在的位置在点和点处,于,于,
已知,,,,试问,图书室应该建在距点多少知处.
才能使它到两所学校的距离相等?
21.一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到,那么梯子的底端在水平方向滑动了几米?
已知,如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.
动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,
如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
t为______时,△PBQ是等边三角形?
(2) P,Q在运动过程中,△PBQ的形状不断发生变化,
当t为何值时,△PBQ是直角三角形?说明理由.
人教版八年级数学下册第十七章《勾股定理》单元复习与检测(解析版)
一、选择题(本大题共有10个小题,每小题3分,共30分)
1 .如图,一棵大树在一次强风中于离地面3m处折断倒下,树干顶部在离根部4m处,
这棵大树在折断前的高度为( )m.
A.3 B.4 C.5 D.8
【答案】D
【分析】根据大树末端部分、折断部分及地面正好构成直角三角形,利用勾股定理解答即可.
【详解】解:由勾股定理得,断下的部分为=5米,折断前为5+3=8米.
2 . ABC中,∠A,∠B,∠C的对边分别记为a,b,c,
由下列条件不能判定ABC为直角三角形的是( )
A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:3
C.a2=c2﹣b2 D.a:b:c=3:4:6
【答案】D
【分析】由三角形内角和定理及勾股定理的逆定理进行判断即可.
【详解】解:A、∠A+∠B=∠C,又∠A+∠B+∠C=180°,则∠C=90°,是直角三角形;
B、∠A:∠B:∠C=1:2:3,又∠A+∠B+∠C=180°,则∠C=90°,是直角三角形;
C、由a2=c2 b2,得a2+b2=c2,符合勾股定理的逆定理,是直角三角形;
D、32+42≠62,不符合勾股定理的逆定理,不是直角三角形.
故选:D.
3.如图是一个直角三角形,它的未知边的长x等于( )
A.13 B. C.5 D.
【答案】B
【分析】由勾股定理得:22+32=x2
【详解】由勾股定理得:22+32=x2
所以,x=
故选:B
4 .张大爷离家出门散步,他先向正东走了30 m,接着又向正南走了40 m,
此时他离家的距离为( )
A.30 m B.40 m C.50 m D.70 m
【答案】C
【分析】画出示意图,然后根据勾股定理直接求得斜边,即为他离家的距离.
【详解】如图,由题意可得,∠ABC=90°,
所以他离家的距离AB==50m,
故选C.
5 . 已知a,b,c是三角形的三边长,如果满足(a-6)2++|c-10|=0,
那么下列说法中不正确的是( )
A.这个三角形是直角三角形 B.这个三角形的最长边长是10
C.这个三角形的面积是48 D.这个三角形的最长边上的高是4.8
【答案】C
【详解】解:∵(a-6)2≥0,+≥0,|c-10|≥0,(a-b)2++|c-10|=0,
∴a-6=0,b-8=0,c-10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴这个三角形是直角三角形,最长边为10,
∵6×8÷2=24,
∴这个三角形面积为24,
∵24×2÷10=4.8.
∴这个三角形最长边上的高为4.8.
故选C.
6.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A.4米 B.5米 C.6米 D.7米
【答案】D
【分析】先求出的长,利用平移的知识可得出地毯的长度.
【详解】解∶在中,米,
故可得地毯长度米,
故选:D.
7.如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则 BC 的长是( )
A.8 B.10 C.12 D.16
【答案】C
【分析】直接利用勾股定理得出AC的长,进而求出BC的长.
【详解】解:∵AD⊥CD,CD=4,AD=3,∴AC==5.
∵∠ACB=90°,AB=13,∴BC==12.
故选C.
8.如图,有一个圆柱,它的高等于,底面上圆的周长等于,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面与点A相对的点B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程是( )
A. B. C. D.
【答案】C
【分析】本题考查的是平面展开-最短路径问题,根据题意得出蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段的长,求出,利用勾股定理求解即可.
【详解】解:根据题意得出:蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段的长,
由题意得:,,
由勾股定理得:,
故选:C.
9 .如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,
梯子底端到左墙角的距离为米,顶端距离地面米若梯子底端位置保持不动,
将梯子斜靠在右墙时,顶端距离地面米,则小巷的宽度为( )
A.米 B.米 C.2米 D.米
【答案】A
【分析】先根据勾股定理求出梯子的长,进而根据勾股定理可得出小巷的宽度.
【详解】
由题意可得:,
在中,
,米,,
,
,
,
,
小巷的宽度为(米).
故选.
10 .如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,
已知大正方形面积为49,小正方形面积为4,若用,表示直角三角形的两直角边(),
下列四个说法:
①,②,③,④.
其中说法正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
【答案】B
【详解】可设大正方形边长为a,小正方形边长为b,所以据题意可得a2=49,b2=4;
根据直角三角形勾股定理得a2=x2+y2,所以x2+y2=49,式①正确;
因为是四个全等三角形,所以有x=y+2,所以x-y=2,式②正确;
根据三角形面积公式可得 ,而大正方形的面积也等于四个三角形面积加上小正方形的面积,所以,化简得2xy+4=49,式③正确;
因为x2+y2=49,2xy+4=49,
所以
所以,因而式④不正确.
故答案为B.
二、填空题(本大题共有6个小题,每小题3分,共18分)
11 .如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,
其实他们仅仅少走了 步路,却踩伤了花草(假设2步为1米).
【答案】
【分析】根据勾股定理即可求解.
【详解】解:根据题意得,“路”的长度,即步,
是步,是步,共步,
∴少走了步,
故答案为:步.
12 .如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为,
正方形A,B,C的面积分别是,,,则正方形的面积是 .
【答案】17
【分析】根据勾股定理有,,,等量代换即可求正方形D的面积.
【详解】如图,
根据勾股定理可知,
∵,,,
∴,
∴正方形D的面积=49-8-10-14=17(cm2);
故答案为:17.
13.一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有 米.
【答案】14/十四
【分析】根据AB和AC的长度,构造直角三角形,根据勾股定理就可求出直角边BC的长.
【详解】解:∵AC⊥BC,
∴∠ACB=90°;
根据勾股定理,得
AC===12,
∴AF=AC+CF=12+2=14(米);
答:发生火灾的住户窗口距离地面14米;
故答案为14.
14.如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,
A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,
则它所走的最短路线长度为________
【答案】125cm
【详解】解:三级台阶平面展开图为长方形,长为100cm,宽为,
则蚂蚁沿台阶面爬行到点最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到点最短路程为,
由勾股定理得,
解得:,
故选B.
15 .如图,圆柱形容器高为12cm,底面周长为10cm.在容器内壁距离容器底部3cm 的点B处有一蚊子,
此时一只壁虎正好在容器外壁,距离容器上沿3cm与蚊子相对的点A处,
则壁虎捕捉蚊子需爬行的最短距离为 (不计壁厚).
【答案】13
【分析】将容器侧面展开,建立A关于EF的对称点,根据两点之间线段最短可知的长度即为所求.
【详解】解:如图,将容器侧面展开,作A关于EF的对称点,
连接,则即为最短距离,
∴=5cm,=3cm,
∴BD=12cm,
=13(cm).
故壁虎捕捉蚊子的最短距离为13cm.
故答案为:13.
16.有一架秋千,当它静止时,踏板离地垂直高度,将它往前推送水平距离时,秋千踏板离地的垂直高度,秋千的绳索始终拉得很直,则绳索长为 .
【答案】
【分析】设秋千的绳索长为,根据题意可得,利用勾股定理可得,再解方程即可得出答案.
【详解】解:在中,
,
设秋千的绳索长为,
则,
故,
解得:,
答:绳索AD的长度是.
故答案为:.
三、解答题(本大题共有6个小题,共52分)
17. 如图所示,一根旗杆升旗的绳垂直落地后还剩余1米,若将绳子拉直,
则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.
【答案】12米.
【详解】解:设旗杆的高为x米,则绳子长为(x+1)米
由题意得
,
解得x=12
答:旗杆的高为12米.
18.如图,有一只小鸟在一棵高的大树树梢上捉虫子,
它的伙伴在离该树,高的一棵小树树梢.上发出友好的叫声,
它立刻以的速度飞向小树树梢,那么这只小鸟至少几秒才可能到达小树和伙伴在一起?
【答案】这只小鸟至少才可能到达小树和伙伴在一起.
【分析】根据题意得: ,,,AB⊥BC,CD⊥BC,过点D作DE⊥AB于点E,连接AD,可得四边形BCDE是矩形, 然后在中,由勾股定理,即可求解.
【详解】解:如图,
根据题意得: ,,,AB⊥BC,CD⊥BC,
过点D作DE⊥AB于点E,连接AD,
∴∠B=∠C=∠BED=90°,
∴四边形BCDE是矩形,
∴,,
∴,
在中,由勾股定理得:
,
∴小鸟所用的时间为.
答:这只小鸟至少才可能到达小树和伙伴在一起.
19 .如图所示,四边形,,,,,,
求四边形的面积.
【答案】
【分析】连接,在直角三角形中,利用勾股定理求出,再利用勾股定理的逆定理判断得到三角形为直角三角形,四边形面积等于三角形面积+三角形面积,求出即可;
【详解】连接,
在中,,
在中,,,
而,
即,
∴,
∴,
∴
.
20 . 为了丰富少年儿童的业余生活,某社区要在如图中的所在的直线上建一图书室,
本社区有两所学校所在的位置在点和点处,于,于,
已知,,,,试问,图书室应该建在距点多少知处.
才能使它到两所学校的距离相等?
【答案】图书室应该建在距点处,才能使它到两所学校的距离相等
【分析】根据题意表示出,的长,进而利用勾股定理求出即可.
【详解】由题意可得:设,则.
,,,
,
,
解得:.
21.一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到,那么梯子的底端在水平方向滑动了几米?
【答案】(1)这个梯子的顶端距地面有24米
(2)梯子的底端在水平方向滑动了8米
【分析】(1)AC=25米,BC=7米,根据勾股定理即可求得的长;
(2)由题意得: =20米,根据勾股定理求得,根据即可求解.
【详解】(1)解:由题意得:AC=25米,BC=7米,∠ABC=90°,
(米)
答:这个梯子的顶端距地面有24米;
(2)由题意得: =20米,
(米)
则:=15-7=8(米),
答:梯子的底端在水平方向滑动了8米.
已知,如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.
动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,
如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
t为______时,△PBQ是等边三角形?
(2) P,Q在运动过程中,△PBQ的形状不断发生变化,
当t为何值时,△PBQ是直角三角形?说明理由.
【答案】(1)12;(2)当t为9或时,△PBQ是直角三角形,理由见解析.
【分析】(1)根据等边三角形的性质解答即可;
(2)分两种情况利用直角三角形的性质解答即可.
【详解】(1)要使,△PBQ是等边三角形,即可得:PB=BQ,
∵在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.
∴AB=36cm,
可得:PB=36-2t,BQ=t,
即36-2t=t,
解得:t=12
故答案为;12
(2)当t为9或时,△PBQ是直角三角形,
理由如下:
∵∠C=90°,∠A=30°,BC=18cm
∴AB=2BC=18×2=36(cm)
∵动点P以2cm/s,Q以1cm/s的速度出发
∴BP=AB-AP=36-2t,BQ=t
∵△PBQ是直角三角形
∴BP=2BQ或BQ=2BP
当BP=2BQ时,
36-2t=2t
解得t=9
当BQ=2BP时,
t=2(36-2t)
解得t=
所以,当t为9或时,△PBQ是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学下册第十七章《勾股定理》单元复习与检测
选择题(本大题共有10个小题,每小题3分,共30分)
如图,一棵大树在一次强风中于离地面3m处折断倒下,树干顶部在离根部4m处,
这棵大树在折断前的高度为( )m.
A.3 B.4 C.5 D.8
2 . ABC中,∠A,∠B,∠C的对边分别记为a,b,c,
由下列条件不能判定ABC为直角三角形的是( )
A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:3
C.a2=c2﹣b2 D.a:b:c=3:4:6
3. 如图是一个直角三角形,它的未知边的长x等于( )
A.13 B. C.5 D.
4 . 张大爷离家出门散步,他先向正东走了30 m,接着又向正南走了40 m,
此时他离家的距离为( )
A.30 m B.40 m C.50 m D.70 m
已知a,b,c是三角形的三边长,如果满足(a-6)2++|c-10|=0,
那么下列说法中不正确的是( )
A.这个三角形是直角三角形 B.这个三角形的最长边长是10
C.这个三角形的面积是48 D.这个三角形的最长边上的高是4.8
6. 如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A.4米 B.5米 C.6米 D.7米
7 . 如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则 BC 的长是( )
A.8 B.10 C.12 D.16
8 . 如图,有一个圆柱,它的高等于,底面上圆的周长等于,在圆柱下底面的点A处有一只蚂蚁,
它想吃到上底面与点A相对的点B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程是( )
A. B. C. D.
9 .如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,
梯子底端到左墙角的距离为米,顶端距离地面米若梯子底端位置保持不动,
将梯子斜靠在右墙时,顶端距离地面米,则小巷的宽度为( )
A.米 B.米 C.2米 D.米
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,
已知大正方形面积为49,小正方形面积为4,若用,表示直角三角形的两直角边(),
下列四个说法:
①,②,③,④.
其中说法正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
填空题(本大题共有6个小题,每小题3分,共18分)
11 .如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,
其实他们仅仅少走了 步路,却踩伤了花草(假设2步为1米).
12 .如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为,
正方形A,B,C的面积分别是,,,则正方形的面积是 .
13.一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有 米.
14.如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,
A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,
则它所走的最短路线长度为________
如图,圆柱形容器高为12cm,底面周长为10cm.在容器内壁距离容器底部3cm 的点B处有一蚊子,此时一只壁虎正好在容器外壁,距离容器上沿3cm与蚊子相对的点A处,
则壁虎捕捉蚊子需爬行的最短距离为 (不计壁厚).
16.有一架秋千,当它静止时,踏板离地垂直高度,将它往前推送水平距离时,秋千踏板离地的垂直高度,秋千的绳索始终拉得很直,则绳索长为 .
三、解答题(本大题共有6个小题,共52分)
17. 如图所示,一根旗杆升旗的绳垂直落地后还剩余1米,若将绳子拉直,
则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.
如图,有一只小鸟在一棵高的大树树梢上捉虫子,
它的伙伴在离该树,高的一棵小树树梢.上发出友好的叫声,
它立刻以的速度飞向小树树梢,那么这只小鸟至少几秒才可能到达小树和伙伴在一起?
19 . 如图所示,四边形,,,,,,
求四边形的面积.
20 . 为了丰富少年儿童的业余生活,某社区要在如图中的所在的直线上建一图书室,
本社区有两所学校所在的位置在点和点处,于,于,
已知,,,,试问,图书室应该建在距点多少知处.
才能使它到两所学校的距离相等?
21.一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到,那么梯子的底端在水平方向滑动了几米?
已知,如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.
动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,
如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
t为______时,△PBQ是等边三角形?
(2) P,Q在运动过程中,△PBQ的形状不断发生变化,
当t为何值时,△PBQ是直角三角形?说明理由.
人教版八年级数学下册第十七章《勾股定理》单元复习与检测(解析版)
一、选择题(本大题共有10个小题,每小题3分,共30分)
1 .如图,一棵大树在一次强风中于离地面3m处折断倒下,树干顶部在离根部4m处,
这棵大树在折断前的高度为( )m.
A.3 B.4 C.5 D.8
【答案】D
【分析】根据大树末端部分、折断部分及地面正好构成直角三角形,利用勾股定理解答即可.
【详解】解:由勾股定理得,断下的部分为=5米,折断前为5+3=8米.
2 . ABC中,∠A,∠B,∠C的对边分别记为a,b,c,
由下列条件不能判定ABC为直角三角形的是( )
A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:3
C.a2=c2﹣b2 D.a:b:c=3:4:6
【答案】D
【分析】由三角形内角和定理及勾股定理的逆定理进行判断即可.
【详解】解:A、∠A+∠B=∠C,又∠A+∠B+∠C=180°,则∠C=90°,是直角三角形;
B、∠A:∠B:∠C=1:2:3,又∠A+∠B+∠C=180°,则∠C=90°,是直角三角形;
C、由a2=c2 b2,得a2+b2=c2,符合勾股定理的逆定理,是直角三角形;
D、32+42≠62,不符合勾股定理的逆定理,不是直角三角形.
故选:D.
3.如图是一个直角三角形,它的未知边的长x等于( )
A.13 B. C.5 D.
【答案】B
【分析】由勾股定理得:22+32=x2
【详解】由勾股定理得:22+32=x2
所以,x=
故选:B
4 .张大爷离家出门散步,他先向正东走了30 m,接着又向正南走了40 m,
此时他离家的距离为( )
A.30 m B.40 m C.50 m D.70 m
【答案】C
【分析】画出示意图,然后根据勾股定理直接求得斜边,即为他离家的距离.
【详解】如图,由题意可得,∠ABC=90°,
所以他离家的距离AB==50m,
故选C.
5 . 已知a,b,c是三角形的三边长,如果满足(a-6)2++|c-10|=0,
那么下列说法中不正确的是( )
A.这个三角形是直角三角形 B.这个三角形的最长边长是10
C.这个三角形的面积是48 D.这个三角形的最长边上的高是4.8
【答案】C
【详解】解:∵(a-6)2≥0,+≥0,|c-10|≥0,(a-b)2++|c-10|=0,
∴a-6=0,b-8=0,c-10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴这个三角形是直角三角形,最长边为10,
∵6×8÷2=24,
∴这个三角形面积为24,
∵24×2÷10=4.8.
∴这个三角形最长边上的高为4.8.
故选C.
6.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A.4米 B.5米 C.6米 D.7米
【答案】D
【分析】先求出的长,利用平移的知识可得出地毯的长度.
【详解】解∶在中,米,
故可得地毯长度米,
故选:D.
7.如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则 BC 的长是( )
A.8 B.10 C.12 D.16
【答案】C
【分析】直接利用勾股定理得出AC的长,进而求出BC的长.
【详解】解:∵AD⊥CD,CD=4,AD=3,∴AC==5.
∵∠ACB=90°,AB=13,∴BC==12.
故选C.
8.如图,有一个圆柱,它的高等于,底面上圆的周长等于,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面与点A相对的点B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程是( )
A. B. C. D.
【答案】C
【分析】本题考查的是平面展开-最短路径问题,根据题意得出蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段的长,求出,利用勾股定理求解即可.
【详解】解:根据题意得出:蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段的长,
由题意得:,,
由勾股定理得:,
故选:C.
9 .如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,
梯子底端到左墙角的距离为米,顶端距离地面米若梯子底端位置保持不动,
将梯子斜靠在右墙时,顶端距离地面米,则小巷的宽度为( )
A.米 B.米 C.2米 D.米
【答案】A
【分析】先根据勾股定理求出梯子的长,进而根据勾股定理可得出小巷的宽度.
【详解】
由题意可得:,
在中,
,米,,
,
,
,
,
小巷的宽度为(米).
故选.
10 .如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,
已知大正方形面积为49,小正方形面积为4,若用,表示直角三角形的两直角边(),
下列四个说法:
①,②,③,④.
其中说法正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
【答案】B
【详解】可设大正方形边长为a,小正方形边长为b,所以据题意可得a2=49,b2=4;
根据直角三角形勾股定理得a2=x2+y2,所以x2+y2=49,式①正确;
因为是四个全等三角形,所以有x=y+2,所以x-y=2,式②正确;
根据三角形面积公式可得 ,而大正方形的面积也等于四个三角形面积加上小正方形的面积,所以,化简得2xy+4=49,式③正确;
因为x2+y2=49,2xy+4=49,
所以
所以,因而式④不正确.
故答案为B.
二、填空题(本大题共有6个小题,每小题3分,共18分)
11 .如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,
其实他们仅仅少走了 步路,却踩伤了花草(假设2步为1米).
【答案】
【分析】根据勾股定理即可求解.
【详解】解:根据题意得,“路”的长度,即步,
是步,是步,共步,
∴少走了步,
故答案为:步.
12 .如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为,
正方形A,B,C的面积分别是,,,则正方形的面积是 .
【答案】17
【分析】根据勾股定理有,,,等量代换即可求正方形D的面积.
【详解】如图,
根据勾股定理可知,
∵,,,
∴,
∴正方形D的面积=49-8-10-14=17(cm2);
故答案为:17.
13.一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有 米.
【答案】14/十四
【分析】根据AB和AC的长度,构造直角三角形,根据勾股定理就可求出直角边BC的长.
【详解】解:∵AC⊥BC,
∴∠ACB=90°;
根据勾股定理,得
AC===12,
∴AF=AC+CF=12+2=14(米);
答:发生火灾的住户窗口距离地面14米;
故答案为14.
14.如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,
A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,
则它所走的最短路线长度为________
【答案】125cm
【详解】解:三级台阶平面展开图为长方形,长为100cm,宽为,
则蚂蚁沿台阶面爬行到点最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到点最短路程为,
由勾股定理得,
解得:,
故选B.
15 .如图,圆柱形容器高为12cm,底面周长为10cm.在容器内壁距离容器底部3cm 的点B处有一蚊子,
此时一只壁虎正好在容器外壁,距离容器上沿3cm与蚊子相对的点A处,
则壁虎捕捉蚊子需爬行的最短距离为 (不计壁厚).
【答案】13
【分析】将容器侧面展开,建立A关于EF的对称点,根据两点之间线段最短可知的长度即为所求.
【详解】解:如图,将容器侧面展开,作A关于EF的对称点,
连接,则即为最短距离,
∴=5cm,=3cm,
∴BD=12cm,
=13(cm).
故壁虎捕捉蚊子的最短距离为13cm.
故答案为:13.
16.有一架秋千,当它静止时,踏板离地垂直高度,将它往前推送水平距离时,秋千踏板离地的垂直高度,秋千的绳索始终拉得很直,则绳索长为 .
【答案】
【分析】设秋千的绳索长为,根据题意可得,利用勾股定理可得,再解方程即可得出答案.
【详解】解:在中,
,
设秋千的绳索长为,
则,
故,
解得:,
答:绳索AD的长度是.
故答案为:.
三、解答题(本大题共有6个小题,共52分)
17. 如图所示,一根旗杆升旗的绳垂直落地后还剩余1米,若将绳子拉直,
则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.
【答案】12米.
【详解】解:设旗杆的高为x米,则绳子长为(x+1)米
由题意得
,
解得x=12
答:旗杆的高为12米.
18.如图,有一只小鸟在一棵高的大树树梢上捉虫子,
它的伙伴在离该树,高的一棵小树树梢.上发出友好的叫声,
它立刻以的速度飞向小树树梢,那么这只小鸟至少几秒才可能到达小树和伙伴在一起?
【答案】这只小鸟至少才可能到达小树和伙伴在一起.
【分析】根据题意得: ,,,AB⊥BC,CD⊥BC,过点D作DE⊥AB于点E,连接AD,可得四边形BCDE是矩形, 然后在中,由勾股定理,即可求解.
【详解】解:如图,
根据题意得: ,,,AB⊥BC,CD⊥BC,
过点D作DE⊥AB于点E,连接AD,
∴∠B=∠C=∠BED=90°,
∴四边形BCDE是矩形,
∴,,
∴,
在中,由勾股定理得:
,
∴小鸟所用的时间为.
答:这只小鸟至少才可能到达小树和伙伴在一起.
19 .如图所示,四边形,,,,,,
求四边形的面积.
【答案】
【分析】连接,在直角三角形中,利用勾股定理求出,再利用勾股定理的逆定理判断得到三角形为直角三角形,四边形面积等于三角形面积+三角形面积,求出即可;
【详解】连接,
在中,,
在中,,,
而,
即,
∴,
∴,
∴
.
20 . 为了丰富少年儿童的业余生活,某社区要在如图中的所在的直线上建一图书室,
本社区有两所学校所在的位置在点和点处,于,于,
已知,,,,试问,图书室应该建在距点多少知处.
才能使它到两所学校的距离相等?
【答案】图书室应该建在距点处,才能使它到两所学校的距离相等
【分析】根据题意表示出,的长,进而利用勾股定理求出即可.
【详解】由题意可得:设,则.
,,,
,
,
解得:.
21.一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到,那么梯子的底端在水平方向滑动了几米?
【答案】(1)这个梯子的顶端距地面有24米
(2)梯子的底端在水平方向滑动了8米
【分析】(1)AC=25米,BC=7米,根据勾股定理即可求得的长;
(2)由题意得: =20米,根据勾股定理求得,根据即可求解.
【详解】(1)解:由题意得:AC=25米,BC=7米,∠ABC=90°,
(米)
答:这个梯子的顶端距地面有24米;
(2)由题意得: =20米,
(米)
则:=15-7=8(米),
答:梯子的底端在水平方向滑动了8米.
已知,如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.
动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,
如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
t为______时,△PBQ是等边三角形?
(2) P,Q在运动过程中,△PBQ的形状不断发生变化,
当t为何值时,△PBQ是直角三角形?说明理由.
【答案】(1)12;(2)当t为9或时,△PBQ是直角三角形,理由见解析.
【分析】(1)根据等边三角形的性质解答即可;
(2)分两种情况利用直角三角形的性质解答即可.
【详解】(1)要使,△PBQ是等边三角形,即可得:PB=BQ,
∵在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.
∴AB=36cm,
可得:PB=36-2t,BQ=t,
即36-2t=t,
解得:t=12
故答案为;12
(2)当t为9或时,△PBQ是直角三角形,
理由如下:
∵∠C=90°,∠A=30°,BC=18cm
∴AB=2BC=18×2=36(cm)
∵动点P以2cm/s,Q以1cm/s的速度出发
∴BP=AB-AP=36-2t,BQ=t
∵△PBQ是直角三角形
∴BP=2BQ或BQ=2BP
当BP=2BQ时,
36-2t=2t
解得t=9
当BQ=2BP时,
t=2(36-2t)
解得t=
所以,当t为9或时,△PBQ是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
