人教版七年级数学下册第五章:相交线与平行线章节练习题 (1)(含解析)
文档属性
| 名称 | 人教版七年级数学下册第五章:相交线与平行线章节练习题 (1)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 167.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-03 20:56:35 | ||
图片预览



文档简介
七年级数学下册第五章 相交线与平行线章节练习题
一、单选题(共10小题,每小题3分,满分30分)
1.如图,和是对顶角的图形个数有( )
A.个 B.个 C.个 D.个
2.如图,点在直线上且若,则的大小为( )
A. B. C. D.
3.下列选项中,过点画的垂线,三角尺放法正确的是( )
A. B. C. D.
4.同学们可仿照图用双手表示“三线八角”图形(两个大拇指代表被截直线,食指代表截线).下面三幅图依次表示( )
A.同位角、同旁内角、内错角 B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角 D.同位角、内错角、对顶角
5.下列说法正确的是( )
A.不相交的两条线段是平行线
B.不相交的两条直线是平行线
C.不相交的两条射线是平行线
D.在同一平面内不相交的两条直线是平行线
6.如图,下列判断错误的是( )
A.因为,所以
B.因为,所以
C.因为,所以
D.因为,所以
7.如图,已知,直角三角尺的直角顶点在直线上.若则等于( )
A. B. C. D.
8.命题:①邻补角互补;②对顶角相等;③同旁内角互补;④两点之间线段最短;⑤直线都相等.其中真命题有( )
A.个 B.个 C.个 D.个
9.观察下面图案,能通过左图平移得到的是( )
A. B. C. D.
10.已知线段,平移线段得到线段端点移到处,端点移到处,且,则的长为( )
A. B. C. D.
二、填空题(共11小题,每小题3分,满分33分)
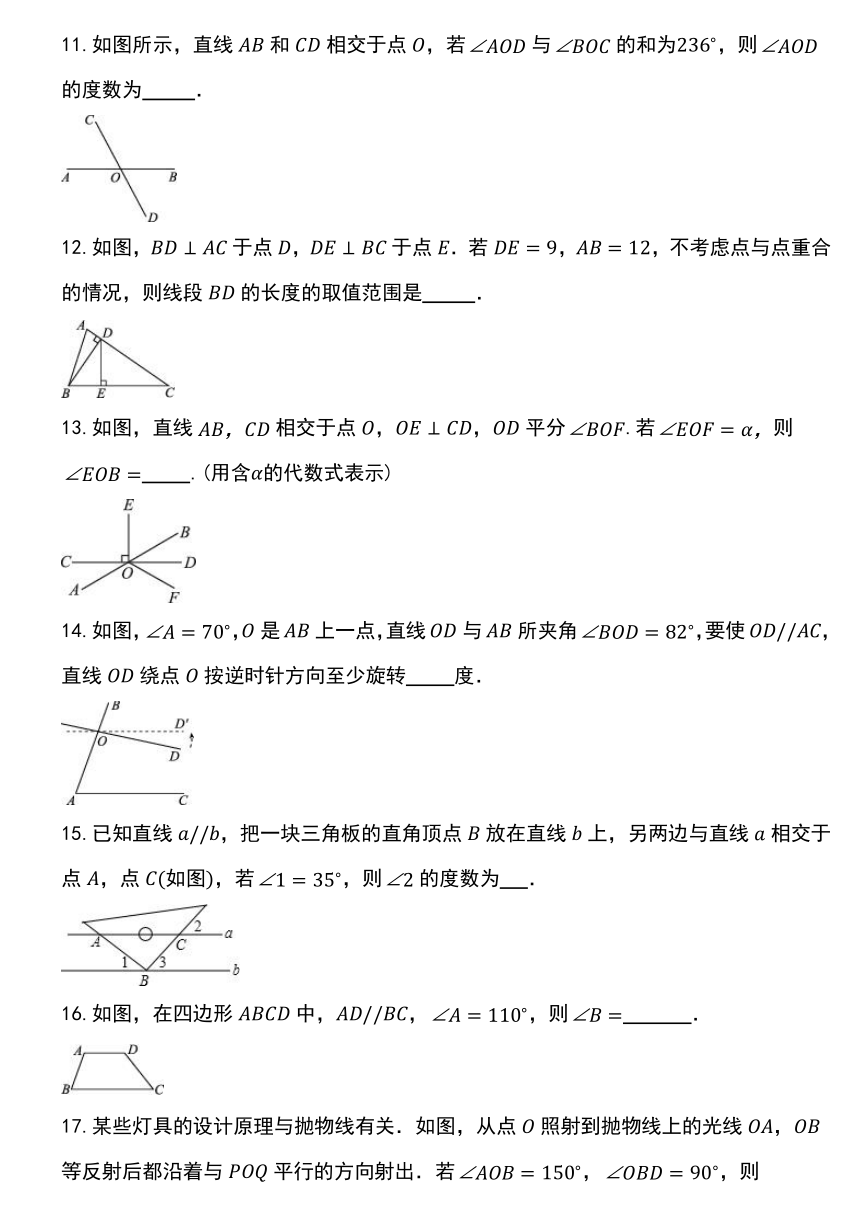
11.如图所示,直线和相交于点,若与的和为,则的度数为 .
12.如图,于点,于点.若,,不考虑点与点重合的情况,则线段的长度的取值范围是 .
13.如图,直线相交于点,,平分.若则 .(用含的代数式表示)
14.如图,,是上一点,直线与所夹角,要使,直线绕点按逆时针方向至少旋转 度.
15.已知直线,把一块三角板的直角顶点放在直线上,另两边与直线相交于点,点如图,若,则的度数为 .
16.如图,在四边形中,,,则 .
17.某些灯具的设计原理与抛物线有关.如图,从点照射到抛物线上的光线,等反射后都沿着与平行的方向射出.若,,则 .
18.如图,则 .
19.“对顶角相等”可以写成“如果 ,那么 ”.
20.一大门的栏杆如图所示,垂直于地面于点,平行于地面,则 .
21.如图是一块长方形的场地,长,宽.从,两处入口的小路宽都为,两条小路汇合处宽为,其余部分种植草坪,则草坪的面积为 .
三、解答题(共6小题,满分37分)
22.如图,三角形平移后的图形是三角形,其中与是对应点,请画出平移后的三角形.
23.如图,已知,,,与平行吗?为什么?
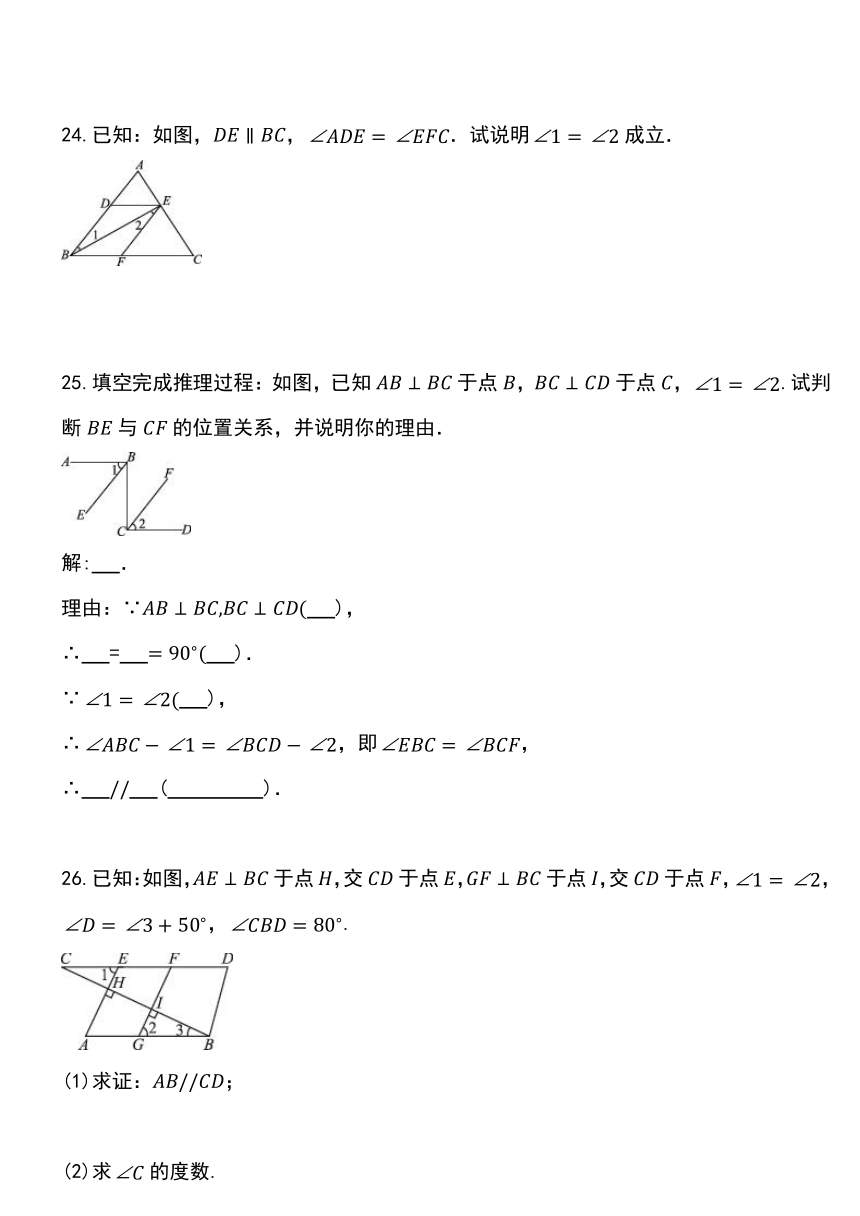
24.已知:如图,,.试说明成立.
25.填空完成推理过程:如图,已知于点,于点,.试判断与的位置关系,并说明你的理由.
解: .
理由:∵ ),
∴ = ).
∵ ),
∴,即,
∴ ( ).
26.已知:如图,于点,交于点,于点,交于点,,,.
(1)求证:;
(2)求的度数.
27.如图在三角形中将三角形沿方向向右平移得到三角形.
(1)求的度数
(2)若求出的长度
参考答案
1.A
【解析】一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角据此作答即可.
解:只有丙图中的两个角是对顶角,
故选:.
本题考查了对顶角的概念,解题的关键是掌握对顶角的概念.
2.B
【解析】首先由,根据垂直的定义,得出,然后由平角的定义,知,从而得出的度数.
解:,
,
,
.
故选:.
本题主要考查了垂直及平角的定义,题目简单.
3.C
【解析】过点画的垂线,则点在上,,所以三角尺放法正确的为
.
故选:C.
4.B
【解析】根据同位角、内错角、同旁内角的概念,可知第一个图是同位角,第二个图是内错角,第三个图是同旁内角. 故选.
5.D
【解析】平行线需满足以下三个条件:
(1)必须是同一平面内;
(2)不相交;
(3)直线.
故选D.
6.C
7.B
【解析】因为直角三角尺的直角顶点在直线上,
所以.
所以.
8.C
【解析】①邻补角互补,正确; ②对顶角相等,正确; ③若被截线不平行,则同旁内角不互补,故错误; ④两点之间线段最短,是线段的性质,正确; ⑤直线是向两方无限延伸的,没有长短,故错误.故①②④正确,共个
9.C
10.A
11.
【解析】由对顶角相等,得
12.
【解析】是直线外一点,,是点与直线上两点连接得到的线段,根据垂线段最短,可得.是直线外一点,是点与直线上两点连接得到的线段,根据垂线段最短,可得,所以.
13.
【解析】于点
.
又
.
平分
.
14.
15.
【解析】由,,根据平角的定义,即可求得的度数,又由直线,根据两直线平行,同位角相等,即可求得的度数.
解:,,
,
直线,
.
故答案为:.
此题考查了平行线的性质与平角的定义解题的关键是掌握两直线平行,同位角相等的定理的应用.
16.
【解析】
.
又,
.
17.
【解析】,,
,
,
,
,
故答案为:.
18.
【解析】
.
.
19.两个角为对顶角
;这两个角相等
【解析】∵原命题的条件是:“两个角是对顶角”,结论是:“它们相等”,
∴命题“对顶角相等”写成“如果那么”的形式为:“如果两个角为对顶角,那么这两个角相等”.
故答案为两个角为对顶角;这两个角相等.
20.
【解析】过点作于点,则
,,
,
,
.
21.
【解析】由图形可看出,种植草坪的部分正好可以拼成一个长方形,
且这个长方形的长为,
这个长方形的宽为,
因此,草坪的面积.
故答案为.
22.解:如图所示:
23.解:平行.
理由:因为,,
所以.
因为,
所以,
所以
24.解:因为,
所以两直线平行,同位角相等).
又因为,
所以,
所以同位角相等,两直线平行),
所以两直线平行,内错角相等).
25.解:.
理由:∵(已知),
∴(垂直的定义).
∵(已知),
∴,即,
∴(内错角相等,两直线平行).
26.(1)证明:,,,,.又,,.
(2),,即.,,,.,.
27.(1)三角形沿方向向右平移得到三角形
(2)三角形沿方向向右平移得到三角形即.
一、单选题(共10小题,每小题3分,满分30分)
1.如图,和是对顶角的图形个数有( )
A.个 B.个 C.个 D.个
2.如图,点在直线上且若,则的大小为( )
A. B. C. D.
3.下列选项中,过点画的垂线,三角尺放法正确的是( )
A. B. C. D.
4.同学们可仿照图用双手表示“三线八角”图形(两个大拇指代表被截直线,食指代表截线).下面三幅图依次表示( )
A.同位角、同旁内角、内错角 B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角 D.同位角、内错角、对顶角
5.下列说法正确的是( )
A.不相交的两条线段是平行线
B.不相交的两条直线是平行线
C.不相交的两条射线是平行线
D.在同一平面内不相交的两条直线是平行线
6.如图,下列判断错误的是( )
A.因为,所以
B.因为,所以
C.因为,所以
D.因为,所以
7.如图,已知,直角三角尺的直角顶点在直线上.若则等于( )
A. B. C. D.
8.命题:①邻补角互补;②对顶角相等;③同旁内角互补;④两点之间线段最短;⑤直线都相等.其中真命题有( )
A.个 B.个 C.个 D.个
9.观察下面图案,能通过左图平移得到的是( )
A. B. C. D.
10.已知线段,平移线段得到线段端点移到处,端点移到处,且,则的长为( )
A. B. C. D.
二、填空题(共11小题,每小题3分,满分33分)
11.如图所示,直线和相交于点,若与的和为,则的度数为 .
12.如图,于点,于点.若,,不考虑点与点重合的情况,则线段的长度的取值范围是 .
13.如图,直线相交于点,,平分.若则 .(用含的代数式表示)
14.如图,,是上一点,直线与所夹角,要使,直线绕点按逆时针方向至少旋转 度.
15.已知直线,把一块三角板的直角顶点放在直线上,另两边与直线相交于点,点如图,若,则的度数为 .
16.如图,在四边形中,,,则 .
17.某些灯具的设计原理与抛物线有关.如图,从点照射到抛物线上的光线,等反射后都沿着与平行的方向射出.若,,则 .
18.如图,则 .
19.“对顶角相等”可以写成“如果 ,那么 ”.
20.一大门的栏杆如图所示,垂直于地面于点,平行于地面,则 .
21.如图是一块长方形的场地,长,宽.从,两处入口的小路宽都为,两条小路汇合处宽为,其余部分种植草坪,则草坪的面积为 .
三、解答题(共6小题,满分37分)
22.如图,三角形平移后的图形是三角形,其中与是对应点,请画出平移后的三角形.
23.如图,已知,,,与平行吗?为什么?
24.已知:如图,,.试说明成立.
25.填空完成推理过程:如图,已知于点,于点,.试判断与的位置关系,并说明你的理由.
解: .
理由:∵ ),
∴ = ).
∵ ),
∴,即,
∴ ( ).
26.已知:如图,于点,交于点,于点,交于点,,,.
(1)求证:;
(2)求的度数.
27.如图在三角形中将三角形沿方向向右平移得到三角形.
(1)求的度数
(2)若求出的长度
参考答案
1.A
【解析】一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角据此作答即可.
解:只有丙图中的两个角是对顶角,
故选:.
本题考查了对顶角的概念,解题的关键是掌握对顶角的概念.
2.B
【解析】首先由,根据垂直的定义,得出,然后由平角的定义,知,从而得出的度数.
解:,
,
,
.
故选:.
本题主要考查了垂直及平角的定义,题目简单.
3.C
【解析】过点画的垂线,则点在上,,所以三角尺放法正确的为
.
故选:C.
4.B
【解析】根据同位角、内错角、同旁内角的概念,可知第一个图是同位角,第二个图是内错角,第三个图是同旁内角. 故选.
5.D
【解析】平行线需满足以下三个条件:
(1)必须是同一平面内;
(2)不相交;
(3)直线.
故选D.
6.C
7.B
【解析】因为直角三角尺的直角顶点在直线上,
所以.
所以.
8.C
【解析】①邻补角互补,正确; ②对顶角相等,正确; ③若被截线不平行,则同旁内角不互补,故错误; ④两点之间线段最短,是线段的性质,正确; ⑤直线是向两方无限延伸的,没有长短,故错误.故①②④正确,共个
9.C
10.A
11.
【解析】由对顶角相等,得
12.
【解析】是直线外一点,,是点与直线上两点连接得到的线段,根据垂线段最短,可得.是直线外一点,是点与直线上两点连接得到的线段,根据垂线段最短,可得,所以.
13.
【解析】于点
.
又
.
平分
.
14.
15.
【解析】由,,根据平角的定义,即可求得的度数,又由直线,根据两直线平行,同位角相等,即可求得的度数.
解:,,
,
直线,
.
故答案为:.
此题考查了平行线的性质与平角的定义解题的关键是掌握两直线平行,同位角相等的定理的应用.
16.
【解析】
.
又,
.
17.
【解析】,,
,
,
,
,
故答案为:.
18.
【解析】
.
.
19.两个角为对顶角
;这两个角相等
【解析】∵原命题的条件是:“两个角是对顶角”,结论是:“它们相等”,
∴命题“对顶角相等”写成“如果那么”的形式为:“如果两个角为对顶角,那么这两个角相等”.
故答案为两个角为对顶角;这两个角相等.
20.
【解析】过点作于点,则
,,
,
,
.
21.
【解析】由图形可看出,种植草坪的部分正好可以拼成一个长方形,
且这个长方形的长为,
这个长方形的宽为,
因此,草坪的面积.
故答案为.
22.解:如图所示:
23.解:平行.
理由:因为,,
所以.
因为,
所以,
所以
24.解:因为,
所以两直线平行,同位角相等).
又因为,
所以,
所以同位角相等,两直线平行),
所以两直线平行,内错角相等).
25.解:.
理由:∵(已知),
∴(垂直的定义).
∵(已知),
∴,即,
∴(内错角相等,两直线平行).
26.(1)证明:,,,,.又,,.
(2),,即.,,,.,.
27.(1)三角形沿方向向右平移得到三角形
(2)三角形沿方向向右平移得到三角形即.
